恰当地应用策略培养数学学习迁移能力

2017-02-01孙颖

文化创新比较研究 2017年22期

孙颖

（宁夏回族自治区石嘴山市第二中学，宁夏石嘴山 753200）

学习迁移是一种学习对另一种学习的影响。其涵义包括了前一种学习对后一种学习的影响，也包括了后一种学习对前一种学习的影响。学习的实质是把学得的知识经验（包括概念、原理、原则、技能、技巧、方法等）加工重组改变后，运用于新情境的过程。学习者在进行迁移前所掌握的知识叫做源知识，学习者将要学习的知识叫做目标知识，如果学习者将源知识运用到了目标知识的学习，或阻碍或促进了学习，我们就说发生了迁移。

学习迁移现象尤其在知识的学习和技能的学习中最为明显。学习正迁移能给学习者带来事半功倍的效率，使得课堂教学高效化。如果我们教师能在教学中较好地利用迁移条件，选择内容、改进教学，就能大大提高课堂教学效果。学习迁移对整个教学活动都具有指导意义。

关于迁移的思想可以追溯到中国古代教育家孔子《论语·述而》中，孔子说：“举一隅不以三隅反，则不复也”。在教学中正确引导学生从实践经验和已有的知识中学习数学和理解数学，有效地利用数学知识的迁移，促进学生获得新的知识和技能，顺利的消除学习新知识的心理障碍，把思维引到新知识中，是发展学生思维、提高学生学习能力的一个有效措施。但在进行学习迁移的过程中，要注意策略的选择和应用。

1 新旧知识之间的联系

深刻理解和牢固掌握已有的知识将有助于新知识的学习。在通过一定次数的训练，使已学的知识保持较高水平的清晰度、辨别性和可利用性，在学习新知识时，学生能够很快意识到新旧知识间的联系，从而较快地找到解决新问题的突破点，这就要求学生事先要建立稳定清晰的知识结构体系，方便于学习的迁移。

例：（人教版八年级上册第42页探究题）如图1，要在燃气管道上修建一个泵站，分别向A、B两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短？你可以在l上找几个点试一试，能发现什么规律？这道题的综合性很强，包括的知识点有轴对称、三角形两边之和大于第三边、线段垂直平分线的性质定理等。所以，学生如果对这些知识点理解不到位，无法建立起这些知识点与本道题之间的有效联系的话，那么这道题老师无论讲多少遍，学生恐怕都听天书。从实际教学效果来看，这道题学生的确掌握的很不好，就是因为对知识理解的不到位，严重影响了学习的正迁移。

图1

拓展题目：如图2所示，正方形ABCD的边长为a，E是BC边上一点，且AE＝8，F是BD上一动点。（1）试判断AF和FC的数量关系，并说明理由。（2）设折线EFC的长为b，求b的最小值，并说明此时点F的位置。

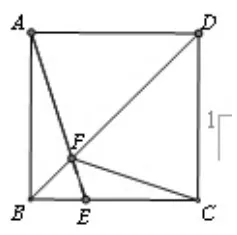
图2

在前面解题经验的基础上，教师只要稍加点拨，学生便会触类旁通，很快确定，当点F与AE和BD的交点重合时，这时b的值最小，即b＝8。

这种拓展能够激起学生学习和探究的欲望，使得学生对所学知识产生浓厚的兴趣，形成一种急切的应用数学知识解决问题的愿望，这样使得知识的迁移落到了实处，教学收到了良好的效果。

2 提高对基本原理的理解水平，促进迁移

在学习中，相似原理和法则的迁移是常见的迁移现象。要促进原理的迁移，就要准确理解原理，正确运用原理，提高解决实际问题的能力。在学习中，让学生自己通过研究、思考，总结出原理、法则，充分掌握运用原理的条件、方法、途径和手段，就更有助于学习的迁移。例如：如图3，点D、E分别为△ABC边AB、AC的中点。求证：DE∥BC且为了让学生能够充分的理解命题的内容，并形成解决问题的方法，笔者用几何画板特意做了如下动画（见图4～6），让学生观察交流，归纳出证明的方法。

这个过程，帮助学生很好的理解了这一数学原理的同时，也帮助学生掌握了这类题目的解答规律和解题方法。真正实现“授之以渔”的目的，切实把学生从题海中解救出来。拓展、已知：如图7，在四边形ABCD中，E、F、G、H 分别是 AB、BC、CD、DA 的中点。求证：四边形EFGH是平行四边形。只要学生充分理解了三角形中位线定理，通过构造三角形便迎刃而解。

图3

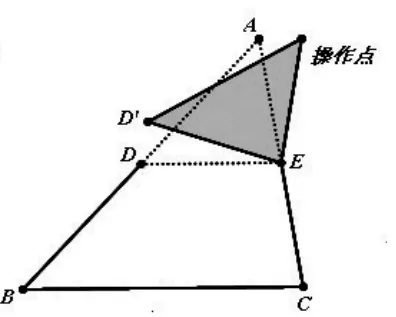
图4

图5

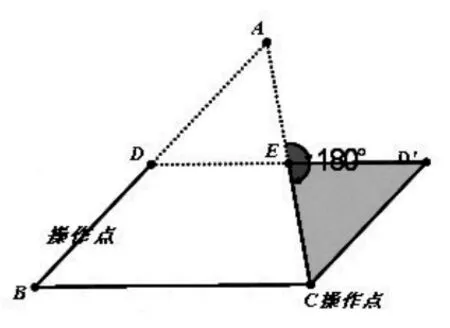
图6

图7

3 选择恰当的学习方法

学生逐渐形成了学习方法和习惯，而这些学习方法和习惯对新知识的学习可能起积极作用，也可能起消极作用，为了避免负迁移的发生，应该及时给学生适当的指导。一方面要把学习的方法教给学生，如理解知识的最好途径、复习和巩固知识的方法、解决问题的方法的选择等；另一方面，要组织、引导学生总结经验，开展学习经验交流，不断更新学习方法，以便新知识的获取和问题的解决。

图8

4 加强有指导的数学活动

数学活动和数学教学活动不同。数学教学活动是老师策划，学生是被动的；而在数学活动中，“教师是学生学习的组织者、引导者与合作者”，是参与数学活动的一份子。所以，有效的活动型学习更易于迁移到新情境中去。在活动中，学生能独立思考得出自己的结论，有利于学生主动性的发展。活动可以使学生得到益处，但如果对数学活动加以指导，便可以增加迁移。例如：笔者侄子上一年级，在他的练习册中有这样一道创新题：一根绳子被剪6次，会得到几段绳子？这道题只是让6岁多的孩子去想答案，比较困难；直接告诉他答案，这就与初衷背道而驰。于是，笔者给他一根绳子，一把小剪刀，剪6次试试。他很快得出了答案。为了考察笔者侄子是否能理解这道题的意图，并且举一反三，笔者又将这道题拓展：如果剪7次，会得到几段绳子？回答得很快：8段。笔者很高兴。因为类似这样的问题，笔者在问自己的学生（初中生）时，还有人答不上来。是啊，这种题目在我们成人看来，太小儿科了。可是对于一个心智还很不成熟的儿童来说，已经不错了。因此，作为一线教师来说，要站在学生的思维角度引导学生，适时、适当地指导学生进行有效的数学活动，不但能增加学生的体验，获得数学活动经验，掌握解决问题的方法；同时还能帮助学生很好的理解数学，对学生学习迁移能力的培养都是不无裨益的。

再如：在△ABC中，已知∠B=∠C，求证：AB=AC。受到等腰三角形“三线合一”性质的启发，学生会想到通过做BC边上的高线或作∠A的角平分线完成；但如果做BC边上的中线，则无法完成证明。为了让学生对此有深刻的影响，笔者刻意让学生去尝试。费了好大的劲，学生突然明白了老师的用意，在“埋怨”当中顺利的掌握了等腰三角形判定定理的证明。这种数学活动经验使得学生对知识的理解更为深刻，为学习正迁移又增加了一份保障。