适用于双馈风电场联络线的距离保护方案

杨增力孔祥平王力军张 哲周虎兵

（1. 国网湖北省电力公司 武汉 430077 2. 国网江苏省电力公司电力科学研究院 南京 211103 3. 强电磁工程与新技术国家重点实验室（华中科技大学） 武汉 430074）

适用于双馈风电场联络线的距离保护方案

杨增力1孔祥平2王力军1张 哲3周虎兵1

（1. 国网湖北省电力公司 武汉 430077 2. 国网江苏省电力公司电力科学研究院 南京 211103 3. 强电磁工程与新技术国家重点实验室（华中科技大学） 武汉 430074）

风电场联络线作为风电场向电网输送功率的重要通道，其稳定运行对于风电场和电网的安全稳定运行具有重要影响。双馈风电机组故障电流特性复杂，将导致基于全波傅里叶算法的传统距离保护应用在双馈风电场联络线上时性能严重劣化，难以满足实际电网安全运行要求。因此提出一种距离保护方案。该方案以瞬时值表征的微分方程算法为基础，通过数字低通滤波、故障点电压重构和故障距离迭代计算等技术保证距离测量的正确性。仿真结果表明，该距离保护方案的整体性能明显优于传统距离保护方案，可较好地满足工程应用要求。

双馈风电场 联络线保护 距离保护 保护算法 仿真分析

0 引言

近年来，随着风电并网容量的快速增长，双馈感应发电机（Doubly-Fed Induction Generator, DFIG）作为风力发电技术的主流方案，其应用也越来越广泛[1-3]。受自然条件、地理环境等因素的限制，DFIG难以像光伏发电机组一样实现分布式、就地并网。因此，DFIG一般采用单元接线方式，并联分组后就地形成集约式风电场，然后经过升压变压器，通过联络线连接到配电网或输电网中[4]。双馈风电场联络线作为风电场向电网输送功率的重要通道，其运行安全对于风电场和电网的安全稳定运行都具有重要意义。因此，电网故障时确保双馈风电场联络线保护正确、可靠的动作对风电场和电网至关重要。

双馈风电场的运行方式受气候条件等因素的影响，具有明显的随机性和间歇性[5-7]。鉴于距离保护，特别是距离保护Ⅰ段受系统运行方式变化的影响较小，许多学者推荐采用距离保护作为联络线的主保护或后备保护[8]，以保证双馈风电场联络线的运行安全。进一步地，文献[9-11]提出了距离保护的自适应整定方案，以应对双馈风电场运行方式变化的影响。

这些传统的或自适应整定的距离保护动作的基本原则是：利用保护安装处测量得到的电压和电流中的基频分量，计算保护安装处与故障点之间的视在阻抗，并以此来判断是否为区内故障。然而，对DFIG故障电流特性的分析表明[12-16]，其变化特征与传统同步发电机馈出的故障电流存在较大差异，导致上述基于全波傅里叶算法的距离保护方案的测量阻抗无法正确反应故障距离。这意味着，其应用于双馈风电场联络线上时，保护性能严重劣化[17-21]，难以满足实际应用要求。

为了解决基于全波傅里叶算法的距离保护方案应用在双馈风电场联络线上所面临的问题，本文提出了一种由输电线路微分方程、低通滤波、故障点电压重构和故障距离迭代计算四部分构成的距离保护方案，该方案以瞬时值表征的微分方程算法为基础构成，因此，其性能不受DFIG复杂故障电流特性的影响。采用低通滤波器有效消除了测量电压和电流中高频分量对微分方程算法的影响。通过对故障点电压进行重构，保证经过低通滤波后，保护安装处测量得到的电压、电流以及故障点电压等电气参数仍符合原始输电线路参数模型。仿真算例表明，本文提出的距离保护方案的整体性能明显优于传统距离保护方案。

1 基于全波傅里叶算法的距离保护存在的问题

随着风电并网容量的不断增长，新并网规程要求风电机组必须具备低电压穿越运行能力[22]。为了提高DFIG的低电压穿越运行能力，一种常用的办法是安装撬棒电路[23]。当电网电压跌落较为严重时，撬棒电路投入，断开转子侧变流器与转子绕组的连接，并通过撬棒电阻将转子绕组短路。撬棒电路的投入，使得双馈电机的短路电流特性更为复杂，给基于全波傅里叶算法的传统距离保护的动作性能带来了诸多不利影响，主要表现在以下三个方面。

（1）在风电场近区发生故障时，撬棒电路将自动投入。由于撬棒电路投入前后，DFIG馈出的故障电流特性发生明显变化，且撬棒电路的投入存在时延，因而导致基于全波傅里叶算法的距离保护算法出现跨数据窗问题，影响测量阻抗的计算精度。

（2）一旦撬棒电路投入，DFIG的故障电流中会出现角频率约等于转子旋转角速度的衰减电流分量[13]，且该电流分量的衰减时间常数很小。一般来说，DFIG允许的转子转速范围为0.7～1.3(pu)，意味着上述衰减电流分量的频率和基频相差不大。因此，上述衰减电流分量的存在会给故障电流基频分量的计算带来较大的误差。

（3）当联络线上发生三相对称故障，撬棒电路投入后，DFIG故障电流中只有角频率分别约等于转子旋转角速度和0的两个衰减电流分量[13]，不存在传统距离保护计算测量阻抗所需的基频分量，从而导致保护失效。

综上，基于全波傅里叶算法的传统距离保护难以直接作为双馈风电场联络线保护使用，需要采用新的保护方案。

2 新型距离保护方案

2.1 输电线路微分方程

下面以输电线路发生单相接地故障为例给出输电线路的R-L微分方程。输电线路单相接地故障模型如图1所示，输电线路在F点处发生A相接地故障，过渡电阻为Rf。

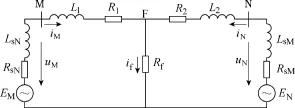
图1 输电线路单相接地故障模型Fig.1 Single-phase-to-ground fault model for transmission line

以母线M为例，保护安装处M测量得到的A相电压为

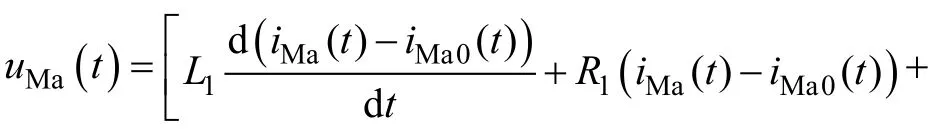
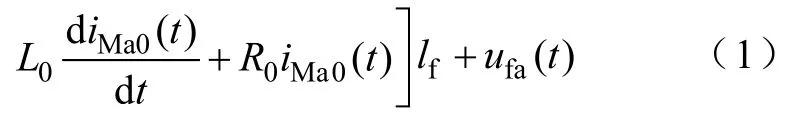
式中，uMa(t)和iMa(t)分别为保护安装处M测量得到的A相电压和电流；iMa0(t)为保护安装处M测量得到的A相电流的零序分量；ufa(t)为故障点F处的A相电压；L1和R1分别为输电线路单位长度的正序电感和电阻；L0和R0分别为输电线路单位长度的零序电感和电阻；lf为从保护安装处M到故障点F处的输电线路长度，即故障距离。

对于式（1）中的微分项，可用式（2）所示的差分算法代替。

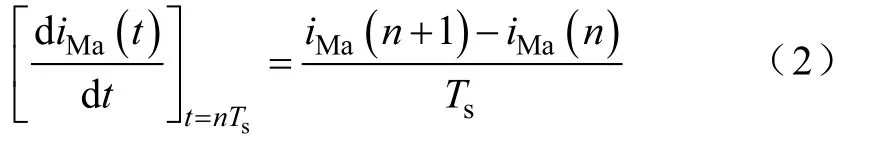
式中，Ts为保护采样周期；n为采样点序号。

将式（2）代入式（1），可得

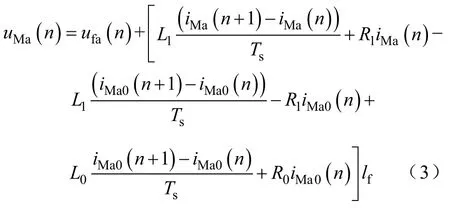
将多点采样数据代入式（3），可以得到一系列的差分方程，从而形成一个差分方程组。然后，利用最小二乘算法对差分方程组进行迭代计算，求解出故障距离lf。

式（3）中的故障点F处的A相电压ufa(n)是以过渡电阻Rf为自变量的函数，需要通过故障点电压重构获得，这将在后续内容中阐述。

2.2 低通滤波

在故障引起的暂态过程中，电压和电流中将出现大量的高频分量，对基于微分方程算法的距离保护性能产生不利影响。因此，需要引入低通滤波器对测量电压和电流中的高频分量进行处理。

二阶巴特沃斯低通滤波器具有最大平坦响应、良好的线性相位特性和便于设计等优点[24]，因此，本文采用二阶巴特沃斯低通滤波器对测量电压和电流进行滤波。二阶巴特沃斯低通滤波器为

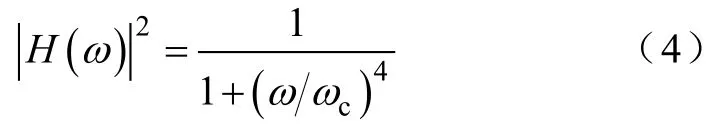
式中，ωc为二阶巴特沃斯低通滤波器的截止角频率。文中，ωc=942.477rad/s，意味着截止频率为150Hz。

虽然经过二阶巴特沃斯低通滤波器后，输出信号和原始输入信号之间存在一定的相位延迟，但是由于电压和电流均通过了该低通滤波器，两者间的相位关系不会发生变化。因此，通过对式（3）所给出的差分方程迭代计算，仍能准确地计算出故障距离。

2.3 故障点电压重构

由式（3）可知，要通过迭代计算得到准确的故障距离，不仅需要获得保护安装处的测量电压和电流，还需要知道故障点电压。但故障点电压对于保护来说是未知的，需通过重构的方法近似获得。

根据输电线路等传变原理[25]，除了保护安装处的测量电压和电流应通过上述二阶巴特沃斯低通滤波器，通过重构获得的故障点电压也应通过相同的低通滤波器，以保证所有电气参数符合原始输电线路的参数模型。若在本文距离保护方案中，故障点重构电压不进行滤波，则可能使故障距离计算结果出现较大的误差，从而导致该距离保护方案出现暂态超越的问题。

基于以上考虑，分成故障发生前、后两个阶段分别对故障点电压进行重构，并将故障点重构电压ufr拆分成两部分，即

式中，ufr1为正常运行情况下的故障点电压；ufr2为过渡电阻的电压降。下面详细阐述ufr1和ufr2的求解过程。

1）故障发生前

电网发生故障前，故障点电压通常为正弦稳态的线路电压。由于故障点位置是无法预知的，因此，可在被保护线路上选取某一点（如线路中点）作为假定的故障点，然后求得正常运行情况下该点的电压作为故障点电压。该情况下满足

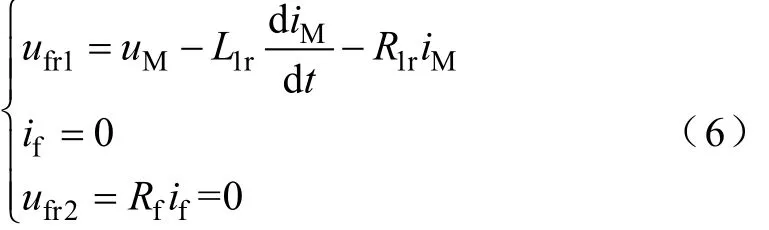
式中，if为流过过渡电阻的故障电流；L1r为保护安装处到假定故障点的线路正序电感；R1r为保护安装处到假定故障点的线路正序电阻。

在被保护线路上，任意选取某一点作为假定故障点的处理方法将对故障距离的计算结果带来一定的误差，但是采用下文将要阐述的迭代算法可以减少这种处理方法所带来的误差。

2）故障发生后

电网故障后的电压重构需要考虑单相接地故障和相间故障两种故障类型。对于单相接地故障，一般情况下，故障点两侧零序阻抗角相差不大，因此，可近似认为过渡电阻上流过的零序电流的相位与保护安装处测量得到的零序电流相位相同，即

式中，C0为保护安装处的零序分流系数。该情况下满足

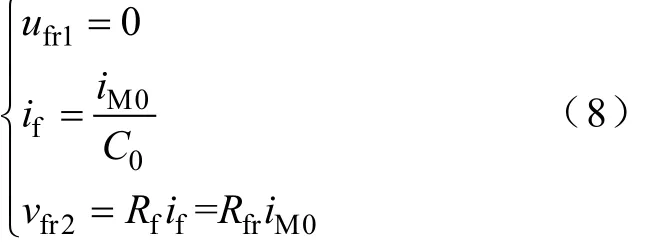
式中，Rfr=C0Rf。

同理，对于经过渡电阻的相间故障，可近似认为过渡电阻上流过的故障电流的相位与保护安装处测量得到的故障相电流相位相同，即

式中，C1为保护安装处的正序分流系数。这种情况满足

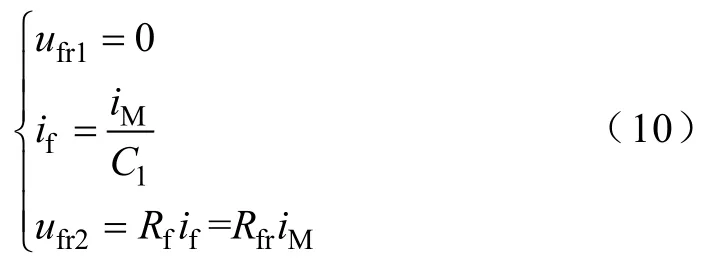
式中，Rfr=C1Rf。

分别将ufr1和iM、iM0经过二阶巴特沃斯低通滤波器处理后得到uf′r1和iM′、iM′0，这样就可以得到经过二阶巴特沃斯低通滤波器处理后的故障点重构电压为

未知数Rfr可通过下文将要阐述的迭代算法求出。若求解得到的Rfr接近零，则认为发生的故障为金属性故障；否则，所发生的故障为经过渡电阻故障。

2.4 故障距离迭代计算

为了减小故障距离计算结果的误差，当检测到故障发生后，采用如下的故障距离迭代计算方法。

（1）定义t0为故障发生时刻，tcal为当前的采样时刻。假设故障点位于线路中点，即设置故障距离的初始迭代值为liter=0.5lwhole，lwhole是被保护线路的全长。

（2）获得当前时刻保护安装处的测量电压和电流的采样值，并利用二阶巴特沃斯低通滤波器对各时刻的测量电压和电流的采样值进行滤波，得到新的测量电压和电流的采样值。

（3）根据2.3节介绍的故障点电压重构原理，计算当前采样时刻的故障点重构电压的采样值。

（4）如果tcal-t0≥T1（取T1=5ms），转至（5）；否则，转至（8）。

（5）将tcal-T1～tcal时间段内的每个采样时刻的保护安装处的测量电压、电流和故障点重构电压的采样值代入式（3），得到一个差分方程组。

（6）利用最小二乘算法对差分方程组进行计算，求解故障距离lcal，并令liter=lcal。

（7）如果tcal-t0≤T3（T3为全部迭代计算结束的最大时间宽度，取T3=40ms），转至（8）；否则，转至（9）。

（8）进行下一次采样，并将tcal更新至最新的采样时刻，转至（2）。

（9）迭代结束。

通过上述迭代计算，可以得到故障发生后5～40ms内每一个采样点的故障距离。

3 仿真

3.1 仿真模型

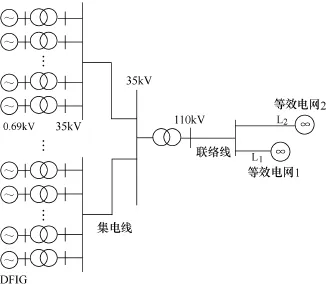
图2 双馈风电场接线Fig.2 DFIG based wind farm connection

典型的双馈风电场接线如图2所示。由于仿真研究主要考虑故障后双馈风电场复杂故障电流特性情况下联络线保护的性能，且故障持续时间较短。因此，在仿真研究过程中，风电场的风速保持不变。

在忽略风电场内部损耗的情况下，即使不同双馈风电机组的故障电流可能不等，但其特征相同。这种情况下，整个双馈风电场可以用单台DFIG等效替代，如图3所示。需要说明的是，这种双馈风电场的等效处理方法对继电保护原理研究的影响可以忽略不计。

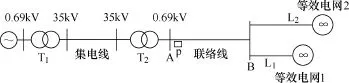
图3 双馈风电场等效模型Fig.3 Equivalent model of DFIG based wind farm

图3中，DFIG的额定容量为100MV·A，额定线电压为690V。定子绕组电阻为0.007 56(pu)，定子漏电抗为0.142 5(pu)，转子绕组电阻为0.005 33(pu)，转子漏电抗为0.142 5(pu)，定转子互感为2.176 7(pu)，转子额定转速为1.2(pu)。变压器T1容量为120MV·A/ 120MV·A，电压比为0.69kV/35.0kV，联结组标号为ynD，漏电抗为8.95%；变压器T2容量为120MV·A/ 120MV·A，电压比为35.0kV/110.0kV，联结组标号为dYN，漏电抗为10.5%；集电线总长度5km，单位长度正序电阻、电抗分别为rC(1)=0.17Ω/km、xC(1)= 0.19Ω/km，单位长度零序电阻、电抗分别为rC(0)= 0.394Ω/km、xC(0)=0.43Ω/km；联络线总长度为100km，单位长度正序电阻、电抗分别为rT(1)= 0.081Ω/km、xT(1)=0.401Ω/km，单位长度零序电阻、电抗分别为rT(0)=0.475Ω/km，xT(0)=1.143Ω/km。此外，线路L1总长度为40km，线路L2总长度为60km，线路L1和L2的其他参数与联络线相同。

3.2 新型距离保护方案性能

为了全面地说明所提出的距离保护方案的性能，下面对不同故障点位置（包括保护区内和保护区外）发生不同类型故障情况下，该距离保护方案的性能进行仿真。在以下仿真算例中，故障发生时刻为t=5s。

3.2.1 区内故障

为了验证保护区内发生故障时本文距离保护方案的动作性能，在联络线上分别选取距母线A 10km、50km和80km的三个故障点。图4～图7分别给了上述三个故障点发生单相金属性接地故障AG、单相经50Ω过渡电阻接地故障AG（50Ω）、BC相间故障和ABC三相对称故障时，本文距离保护方案计算得到的故障距离曲线。

图4 单相金属性接地故障时的故障距离曲线Fig.4 Fault distance curves with single-phase-grounded fault

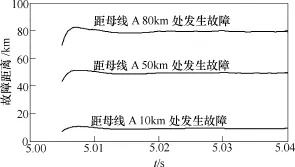
图5 单相经50Ω过渡电阻接地故障时的故障距离曲线Fig.5 Fault distance curves with single-phase-grounded fault via resistance of 50Ω

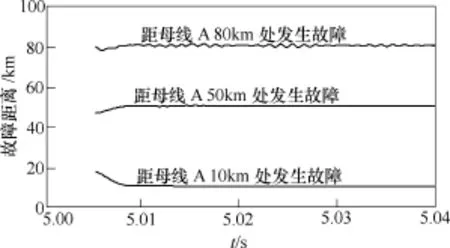
图6 BC相间故障时的故障距离曲线Fig.6 Fault distance curves with phase to phase (BC) fault

图7 三相对称故障时的故障距离曲线Fig.7 Fault distance curves with three-phase symmetrical fault

从图4～图7可以看出，保护区内无论发生何种类型的故障，所提出的距离保护方案计算得到的故障距离均可在10ms内快速趋于稳定，并收敛于实际故障距离。这意味着当保护区内发生故障时，本文距离保护方案能快速、可靠地动作。

3.2.2 区外故障

为了说明保护区外发生故障时本文距离保护方案的动作性能，分别设置了正向区外F1和反向区外F2两个故障点。其中，F1位于线路L1上，距母线B 10km处，F2则位于变压器T1的高压侧母线上。

F1点发生不同类型故障时得到的故障距离曲线如图8所示。从图8中可以看出，当F1点发生单相金属性接地或单相经50Ω过渡电阻接地故障时，虽然本文距离保护方案得到的故障距离计算结果的收敛速度较慢，但仍可收敛于一个稳定值。然而，由于等效电网2提供的助增电流的影响，所得到的故障距离计算结果大于联络线全长。此外，当F1点发生BC相间故障或三相对称故障时，本文距离保护方案得到的故障距离计算结果不能收敛于一个稳定值。因此，当正向区外F1点发生故障时，本文距离保护方案不会误动作。

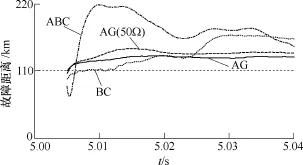
图8 F1点故障时的故障距离曲线Fig.8 The fault distance curves with fault at F1

F2点发生BC相间故障和三相对称故障时的故障距离曲线分别如图9和图10所示。由于变压器T2的联结组标号为dYN，当F2点发生单相接地故障时，联络线上的距离保护方案的起动元件不会动作。因此，当F2点发生单相接地故障时，本文距离保护方案无法得到相应的故障距离曲线。

如图9所示，F2点发生BC相间故障时，虽然本文距离保护方案得到的故障距离计算结果可收敛于一个稳定值，但其值小于0。

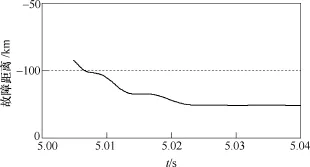
图9 F2点发生BC相间故障时的故障距离曲线Fig.9 Fault distance curve with phase to phase (BC) at F2

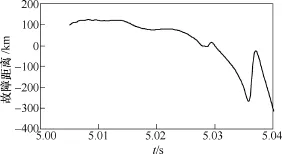
图10 F2点发生三相对称故障时的故障距离曲线Fig.10 Fault distance curve with three-phase symmetrical fault at F2

从图10中可以看出，F2点发生三相对称故障时，本文距离保护方案得到的故障距离计算结果不能收敛于一个稳定值。因此，当反向区外F2点发生故障时，本文距离保护方案不会误动作。

综上，无论保护区内何处发生何种类型的故障，所提出的距离保护方案均能快速、可靠地动作。另一方面，保护区外故障时，本文距离保护方案不会误动作。这说明本文距离保护方案具有优良的动作性能，可以满足电力系统安全稳定运行的要求。

3.3 本文距离保护方案与传统距离保护方案对比

为了对所提出的距离保护方案与传统距离保护方案（基于全波傅里叶算法的距离保护和传统基于微分方程的距离保护）的性能进行对比，本文对联络线上不同位置发生不同类型故障的多种情况进行了仿真研究。由于篇幅所限，下面仅给出联络线中点处发生三相故障和BC相间故障两种故障情况下，联络线保护性能对比，作为典型的仿真算例。

传统距离保护方案是根据保护安装处与故障点之间测量阻抗大小来判断区内、外故障的，而测量阻抗可用故障距离来直观地表示。这意味着，测量阻抗或故障距离的计算准确性决定了传统距离保护方案的性能。因此，在对不同距离保护方案性能进行分析时，可利用故障距离曲线进行对比。

3.3.1 三相故障

假设图3中的风电场联络线中点处在t=5s时发生三相故障，图11分别给出了基于全波傅里叶算法的距离保护方案、传统的基于微分方程算法的距离保护方案和本文提出的基于微分方程算法的距离保护方案计算得到的故障距离曲线。

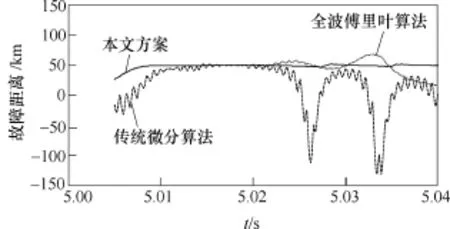
图11 三相对称故障时三种保护方案性能对比Fig.11 Comparison of three protection schemes for three-phase symmetrical fault

由于跨数据窗问题的存在和DFIG故障电流中角频率约等于转子旋转角速度的衰减电流分量的影响，传统的基于全波傅里叶算法的距离保护方案的故障距离计算结果误差较大。另一方面，DFIG故障电流中角频率约等于转子旋转角速度的衰减电流分量不会对所提出的基于微分方程算法的本文距离保护方案造成影响，且本文方案的性能也不受撬棒保护动作行为的影响。因此，本文保护方案计算得到的故障距离的精确度较高。同时由图11也可以看出，本文保护方案的故障距离计算结果在故障发生后10ms内迅速收敛于实际的故障距离，保护动作快速。此外，由于测量电压和电流中的高频分量的影响，传统的基于微分方程算法的距离保护方案的故障距离计算结果不稳定，误差也较大。从图11中曲线对比可以看出，采取低通滤波器可以有效地降低测量电压和电流中高频分量对基于微分方程算法的距离保护方案性能的影响。

3.3.2 BC相间故障

假设图3中的风电场联络线中点处在t=5s时发生BC相间故障，图12分别给出了基于全波傅里叶算法的距离保护方案、传统的基于微分方程算法的距离保护方案和本文提出的基于微分方程算法的距离保护方案计算得到的故障距离曲线。

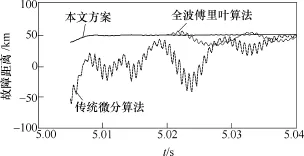
图12 BC相间故障时三种保护方案性能对比Fig.12 Comparison of three protection schemes for phase to phase (BC) fault

如图12中的微分算法曲线所示，由于跨数据窗问题的存在和DFIG故障电流中角频率约等于转子旋转角速度的衰减电流分量的影响，传统的基于全波傅里叶算法的距离保护方案计算得到的故障距离的误差较大。此外，由于测量电压和电流中的高频分量的影响，传统的基于微分方程算法的距离保护方案的故障距离计算结果不稳定，误差也较大，如图12中的传统微分算法曲线所示。然而，如图12中的本文方案曲线所示，所提出的距离保护方案的故障距离计算结果在故障发生后10ms内迅速趋于稳定，并收敛于实际的故障距离。这表明所提出的基于微分方程算法的新型距离保护方案计算得到的故障距离的精确度较高，且保护动作很快。

综上，所提出的距离保护方案的整体性能明显优于传统距离保护方案。

4 结论

为了解决传统保护方案应用在双馈风电场联络线上性能严重劣化的问题，提出了一种基于微分方程算法的距离保护方案，以保障风电场和电网的运行安全。仿真研究表明，所提距离保护方案的整体性能明显优于传统距离保护方案：不受DFIG复杂的故障电流特性的影响，能正确识别区内和区外故障，可较好地满足实际应用要求。

[1] 年珩, 程鹏, 诸自强. 电网电压对称故障时DFIG转子电流的优化控制策略[J]. 电工技术学报, 2014, 29(7): 200-208. Nian Heng, Cheng Peng, Zhu Ziqiang. Optimized control strategy of rotor current for doubly fed induction generators during symmetrical voltage fault[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 200-208.

[2] 宋亦鹏, 年珩. 谐波电网电压下基于矢量谐振控制的双馈异步发电机集成控制策略[J]. 电工技术学报, 2014, 29(7): 187-199. Song Yipeng, Nian Heng. Integrated control strategy of DFIG based on vector resonant control under distorted grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2014, 29(7): 187-199.

[3] 骆皓, 林明耀, 曹阳, 等. 基于暂态磁链前馈补偿的DFIG低穿强励直流灭磁方法[J]. 电工技术学报,2014, 29(9): 64-73. Luo Hao, Lin Mingyao, Cao Yang, et al. Forceful demagnetization of DC component based on transient feedforward compensation during DFIG’s LVRT[J]. Transactions of China Electrotechnical Society, 2014, 29(9): 64-73.

[4] 张保会, 王进, 李光辉, 等. 风力发电机集团式接入电力系统的故障特征分析[J]. 电网技术, 2012, 36(7): 176-183. Zhang Baohui, Wang Jin, Li Guanghui, et al. Analysis on fault features of wind turbine generators concentratedly connected to power grid[J]. Power System Technology, 2012, 36(7): 176-183.

[5] Eriksen P B, Ackermann T, Abildgaard H, et al. System operation with high wind generation[J]. IEEE Power and Energy Magazine, 2005, 3(6): 65-74.

[6] 张丽英, 叶廷路, 辛耀中, 等. 大规模风电接入电网的相关问题及措施[J]. 中国电机工程学报, 2010, 30(25): 1-9. Zhang Liying, Ye Tinglu, Xin Yaozhong, et al. Problems and measures of power grid accommodating large scale wind power[J]. Proceedings of the CSEE, 2010, 30(25): 1-9.

[7] 何世恩, 董新洲. 大规模风电机组脱网原因分析及对策[J]. 电力系统保护与控制, 2012, 40(1): 131-137, 144. He Shien, Dong Xinzhou. Cause analysis on largescale wind turbine tripping and its countermeasures[J]. Power System Protection and Control, 2012, 40(1): 131-137, 144.

[8] 何世恩, 姚旭, 徐善飞. 大规模风电接入对继电保护的影响与对策[J]. 电力系统保护与控制, 2013, 41(1): 21-27. He Shien, Yao Xu, Xu Shanfei. Impacts of largescale wind power integration on relay protection and countermeasures[J]. Power System Protection and Control, 2013, 41(1): 21-27.

[9] 张华中, 王维庆, 朱玲玲, 等. 风电场联络线距离保护的自适应整定方法[J]. 电网技术, 2009, 33（3）: 89-93, 98. Zhang Huazhong, Wang Weiqing, Zhu Lingling, et al. An adaptive setting method for distance protection of transmission lines connecting wind farms[J]. Power System Technology, 2009, 33(3): 89-93, 98.

[10] Pradhan A K, Joos G. Adaptive distance relay setting for lines connecting wind farms[J]. IEEE Transactions on Energy Conversion, 2007, 22(1): 206-213.

[11] Sadegh H. A novel method for adaptive distance protection of transmission line connected to wind farms[J]. International Journal of Electrical Power and Energy Systems, 2012, 43(1): 1376-1382.

[12] 撖奥洋, 张哲, 尹项根, 等. 双馈风力发电系统故障特性及保护方案构建[J]. 电工技术学报, 2012, 27(4): 233-239. Han Aoyang, Zhang Zhe, Yin Xianggen, et al. Research on fault characteristic and grid connectingpoint protection scheme for wind power generation with doubly-fed induction generator[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 233-239.

[13] Pannell G, Atkinson D J, Zahawi B. Analytical study of grid-fault response of wind turbine doubly fed induction generator[J]. IEEE Transactions on Energy Conversion, 2010, 25 (4): 1081-1091.

[14] 郑涛, 魏占朋, 李娟, 等. 计及撬棒保护的双馈风电机组不对称短路电流特性分析[J]. 电力系统保护与控制, 2014, 42(2): 7-12. Zheng Tao, Wei Zhanpeng, Li Juan, et al. Unsymmetrical short circuit current analysis of doubly fed induction generators with crowbar protection[J]. Power System Protection and Control, 2014, 42(2): 7-12.

[15] 孔祥平, 张哲, 尹项根, 等. 计及励磁调节特性影响的双馈风力发电机组故障电流特性[J]. 电工技术学报, 2014, 29(4): 256-265. Kong Xiangping, Zhang Zhe, Yin Xianggen, et al. Fault current characteristics of DFIG considering excitation and regulation characteristics[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 256-265.

[16] Kong X, Zhang Z, Yin X, et al. Study of fault current characteristics of the DFIG considering dynamic response of the RSC[J]. IEEE Transactions on Energy Conversion, 2014, 29(2): 278-287.

[17] 李生虎, 贾树森, 孙莎莎. 风电系统距离Ⅲ段保护动作特性分析[J]. 电力系统自动化, 2011, 35(5): 31-35, 41. Li Shenghu, Jia Shusen, Sun Shasha. Operationcharacteristics analysis of zone 3 distance protection in wind power systems[J]. Automation of Electric Power Systems, 2011, 35(5): 31-35, 41.

[18] 余嘉彦, 袁越, 周建华, 等. 风电场运行参数变化对其出口输电线路距离保护的影响[J]. 电力系统保护与控制, 2011, 39(15): 64-69. Yu Jiayan, Yuan Yue, Zhou Jianhua, et al. Impact of the changes of operation parameters of wind farm on distance protection of output transmission line[J]. Power System Protection and Control, 2011, 39(15): 64-69.

[19] 黄涛, 陆于平, 凌启程, 等. 撬棒电路对风电场侧联络线距离保护的影响及对策[J]. 电力系统自动化, 2013, 37(17): 30-36. Huang Tao, Lu Yuping, Ling Qicheng, et al. Impact of crowbar on wind farm side interconnection line distance protection and mitigation method[J]. Automation of Electric Power Systems, 2013, 37(17): 30-36.

[20] 张保会, 张金华, 原博, 等. 风电接入对继电保护的影响（六）——风电场送出线路距离保护影响分析[J]. 电力自动化设备, 2013, 33(6): 1-6. Zhang Baohui, Zhang Jinhua, Yuan Bo, et al. Impact of wind farm integration on relay protection (6): analysis of distance protection for wind farm outgoing transmission line[J]. Electric Power Automation Equipment, 2013, 33(6): 1-6.

[21] Cho K R, Kang Y C, Kim S S, et al. An ANN based approach to improve the speed of a differential equation based distance relaying algorithm[J]. IEEE Transactions on Power Delivery, 1999, 14(2): 349-357.

[22] 中国电科院. GB/T 19963—2011 风电场接入电力系统技术规定[S]. 北京: 中国标准出版社, 2011.

[23] Morren J, De Haan S W H. Ridethrough of wind turbines with doubly-fed induction generator during a voltage dip[J]. IEEE Transactions on Energy Conversion, 2005, 20(1): 435-441.

[24] Mitra S K. Digital signal processing—a computerbased approach[M].2nd ed. New York: Mc Graw-Hill, 2001.

[25] Wen M, Chen D, Yin X. Instantaneous value and equal transfer processes-based current differential protection for long transmission lines[J]. IEEE Transactions on Power Delivery, 2012, 27(1): 289-299.

Distance Protection Scheme for Interconnection Line of Doubly-Fed Induction Generator Based Wind Farm

Yang Zengli1Kong Xiangping2Wang Lijun1Zhang Zhe3Zhou Hubing1
（1. State Grid Hubei Electric Power Company Wuhan 430077 China 2. State Grid Jiangsu Electric Power Company Research Institute Nanjing 211103 China 3. State Key Laboratory of Advanced Electromagnetic Engineering and Technology Huazhong University of Science and Technology Wuhan 430074 China）

Since the interconnection line of wind farm is the key for power transmission from wind farm to power grid, its operation safety plays an important role to operation stability of power grid. The complicated fault current characteristics of doubly-fed induction generator (DFIG) deteriorate the performance of the conventional distance protection schemes when they are applied on the interconnection lines of DFIG-based wind farm. Therefore, a new distance protection scheme is proposed in this paper. The proposed scheme is based on the R-L differential equation represented by the instantaneous values. Moreover, a series of measures ensures the accuracy of the measured fault distance, such as the low-pass filter, reconstruction of voltage at the fault point and iterative calculation of the fault distance. Simulation cases show that the performance of the proposed distance protection scheme is much better than that of the conventional distance protection schemes.

Doubly-fed induction generator based wind farm, interconnection line protection, distance protection, protection algorithm, simulation study

TM77

杨增力 男，1982年生，博士，高级工程师，研究方向为电力系统继电保护。

E-mail: yangzl8@hb.sgcc.com.cn

孔祥平 男，1988年生，博士，研究方向为应对分布式电源大规模接入的电力系统继电保护及安全稳定控制。

E-mail: kongxphust@163.com（通信作者）

国家自然科学基金资助项目（51177058、51077061）。

2014-09-03 改稿日期 2014-10-25