基于二维调制的级联型整流器负载平衡度限制范围

郑 征 李绍令

（河南理工大学电气工程与自动化学院 焦作 454000）

基于二维调制的级联型整流器负载平衡度限制范围

郑 征 李绍令

（河南理工大学电气工程与自动化学院 焦作 454000）

级联型整流器运行时可能会出现负载不平衡的情况，负载平衡度超出一定范围时直流母线电压将无法保持平衡，此时由其合成的交流侧电压谐波分量增加，导致系统电流的谐波分量也相应增加。在对基于二维调制的平衡控制方式研究的基础上，对单相两级级联整流器的调制波形作深入分析，根据调制波形推导出使两桥直流母线电压能够保持平衡的负载平衡度限制范围。搭建基于Matlab/Simulink的仿真模型和基于RT-lab的半实物实时仿真实验平台，通过仿真和实验验证所作分析与结论的正确性，为无工频变压器级联式功率变换器的设计提供了理论依据。

级联型整流器 负载平衡度限制范围 二维调制 电压平衡

0 引言

级联H桥变换器以H桥电路作为基本能量变换单元，将多个H桥串联起来，单个功率器件承受电压低，可以在交流侧输出较高电压的阶梯波，从而可以将较低耐压等级的功率器件应用于较高电压等级的功率变换场合[1,2]。具有结构简单、模块化程度高、易于多级拓展等突出优点，在高压大功率电力传动、静止无功补偿、新能源发电等场合已得到成功应用[3-5]。

近年来，一种新型的无工频变压器级联式功率变换器引起了人们越来越多的关注。该变换器单相拓扑结构如图1所示，采用高频变压器配合级联H桥整流技术可使高压变流器摆脱工频变压器的限制，且这种结构使得变流器的控制更加灵活[6]。就研究现状来看，该拓扑的级联型整流器仍然存在很多问题有待解决，其中最核心的问题是控制各桥直流母线电压保持平衡[7,8]。因各级联单元流过同一电流，只能依靠这一个电流来调节多个H桥的直流母线电压，即直流母线电压的控制存在耦合现象，使其控制比较困难[9]。

图1 无工频变压器级联式功率变换器单相拓扑结构Fig.1 Single-phase topology of transformerless cascaded converter

目前，级联型整流器的直流母线电压平衡控制方式大体上可分为两类：独立电压闭环控制法和调制波交换平衡法。独立电压闭环控制法，需设置n-1（n为级联单元数）个独立电压闭环，调节各桥交流侧电压的幅值和相位，从而控制各桥直流母线电压稳定在指令值，该方法控制结构复杂，直流母线电压收敛速度慢[6]。调制波交换平衡法首先将各H桥按直流母线电压大小进行排序，然后再根据调制波的大小决定各桥输出，控制各桥直流母线电容进行充放电，使各桥直流母线电压趋于平衡，该方法直接控制各桥PWM波形，控制结构简单，平衡效果好[8]。

文献[6,10]针对单相两级级联整流器采用一种基于二维调制的平衡控制方式，其本质与调制波交换平衡法一致，均采用调制的方式调整各桥在每个开关周期内从网侧所吸收的有功功率，从而控制各桥直流母线电压趋于平衡。基于二维调制的平衡控制方式本质上是对调制波交换平衡法的扩展，其所能提供给两桥的有功功率差值更大，因而其平衡效果更好，直流母线电压恢复平衡速度更快[6]，本文对该平衡控制方式作进一步研究。

受后级电路的影响，级联型整流器运行时各桥的输出功率可能产生差异，这种差异可等效为各桥直流侧连接不平衡负载。但其不平衡程度不能无限制的增大，受两桥所能获得的有功功率最大差值的限制，两桥负载平衡度有一个临界值。超出临界值时，两桥直流母线电压将不再保持平衡，此时由其合成的交流侧电压的谐波分量增加，导致系统电流的谐波分量也相应增加。针对该问题，本文推导出使两桥直流母线电压能够保持平衡的负载平衡度限制范围。

1 级联型整流器整体控制结构

单相两级级联整流器拓扑结构如图2所示，该拓扑基于占空比的数学模型如式（1）所示[11]。

图2 单相两级级联整流器拓扑结构Fig.2 Topology of single-phase two cascaded rectifier

式中，us、is分别为网侧电源电压和输入电流；R为交流回路等效电阻，为电源内阻与电抗器电阻之和；L为交流侧电感；Di为第i（i=1,2）个单元的占空比，其取值范围为[-1,1]；Ucon为两桥交流侧总电压ucon在一个开关周期内的平均值；Ci、Ri、udci分别为第i个单元的直流母线电容、等效负载电阻和直流母线电压。

图3 级联型整流器整体控制框图Fig.3 Overall control block diagram of cascaded rectifier

图4 级联型整流器前馈解耦控制框图Fig.4 Feed-forward decoupling control block diagram of cascaded rectifier

2 基于二维调制的平衡控制方式

文献[6,10]采用一种基于二维调制的平衡控制方式，其控制准则是使直流母线电压较低的桥在每个开关周期内吸收最多的有功功率，使直流母线电压较高的桥在每个开关周期内吸收最少的有功功率。两桥交流侧电压u1、u2在任意一个开关周期内的平均值U1、U2均可取[-udci，udci]内的任意值，将两者分别作为二维平面的横轴和纵轴，由U1、U2合成Ucon的调制区域如图5中虚线框所示。

定义该区域内与横轴成135°的斜线为β 曲线，同一条β 曲线上的所有调制点所对应的Ucon全部相等，可以选择该β 曲线上的任意调制点来合成这个Ucon。ucon为按正弦规律变化的阶梯波，其所对应的β 曲线在(-1,-1)与(1,1)之间按正弦规律周期往返。定义工频周期内调制点的轨迹为α 曲线，当每条β曲线都选择中点作为调制点时，α 曲线为一条与横轴成45°的斜线，称此α 曲线为平分曲线。

图5 二维调制平面Fig.5 Two-dimensional modulation plane

当两桥直流母线电压相等时，显然采用平分曲线能够使两桥获取相等的有功功率；但在两桥直流母线电压不相等时，平分曲线已不再适用。假设udc1＜udc2，在ucon与is同号时，采用图6中粗线所示的调制轨迹，两桥占空比见表1[6]。

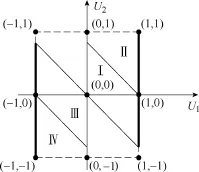
图6ucon与is同号时的调制轨迹Fig.6 Modulation trajectory whenuconandisare the same sign

表1ucon与is同号时的两桥占空比Tab.1 The duty ratios of the two H bridges whenuconandisare the same sign

由于开关周期远小于工频周期，可近似认为udci和is在一个开关周期内保持不变，在区间Ⅰ内两桥在每个开关周期内吸收的有功功率如式（2）所示。U1始终取最大值udc1，则U2的取值为最小，此时桥1从网侧吸收有功功率，桥2向网侧发出有功功率，另有一部分有功功率被负载消耗[6]。

在区间Ⅱ内，两桥在每个开关周期内吸收的有功功率如式（3）所示，此时桥1仍最大程度地从网侧吸收有功功率。为保证对Ucon的合成，桥2将从网侧吸收一部分有功功率[6]。区间Ⅲ与区间Ⅳ内的有功功率传递情况与区间Ⅰ、Ⅱ类似，不再赘述。

在ucon与is同号时，采用图7中粗线所示的调制轨迹，两桥占空比见表2，有功功率传递情况与ucon、is同号时类似[6]，这里不再详细介绍。

图7ucon与is异号时的调制轨迹Fig.7 Modulation trajectory whenuconandisare the opposite sign

表2ucon与is异号时的两桥占空比Tab.2 The duty ratios of the two H bridges whenuconandisare the opposite sign

3 负载平衡度限制范围

3.1 调制波形

采用图6中的调制轨迹时，两桥占空比见表1。ucon＞0时，桥1的占空比始终为1；ucon＜0时，桥1的占空比始终为-1。桥2的占空比为使两桥能够合成Ucon的相应值。在一个工频周期内的两桥调制波形如图8所示。同理，采用图7中的调制轨迹时，在一个工频周期内的两桥调制波形如图9所示。

系统单位功率因数运行时，各相量间的相位关系如图10所示，由于交流回路等效电阻R很小，对系统影响不大，这里将其忽略，uconm滞后is的角度为θ，两者在一个工频周期内的波形如图11所示，其中Uconm、Im分别为uconm、is的幅值。

图8ucon与is同号时的两桥调制波形Fig.8 Modulation waveforms whenuconandisare the same sign

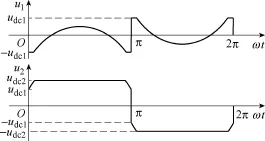
图9ucon与is异号时的两桥调制波形Fig.9 Modulation waveforms whenuconandisare the opposite sign

图10 系统单位功率因数运行时各相量间的相位关系Fig.10 Phase relationship between the phasors when the system is in unity power factor state

图11 一个工频周期内uconm与is的波形Fig.11 Waveforms ofuconmandisin one power frequency cycle

由图11可以看出，uconm与is在0～π-θ之间与π～2π-θ之间同号，采用图6中的调制轨迹；uconm与is在π-θ～π之间与2π-θ～2π之间异号，采用图7中的调制轨迹。那么在整个工频周期内的两桥调制波形如图12所示。

3.2 临界负载平衡度的计算

由3.1节的分析可以看出，图12中的调制波形相比图8左移角度为θ，保持与is同相位；同时由于桥2的调制波形峰值不能大于udc2，桥1的调制波形不是完整的方波，有两块类似三角形的小缺口，如图12中阴影部分所示。一般情况下θ的值比较小，尤其是在负载较小的情况下基本可忽略不计，因而这两个阴影部分面积很小。另外，级联型整流器在这两个部分调制时，is在过零点附近，其值也比较小，那么在两桥有功能量的分配方面由这两个阴影部分所造成的影响也非常小。因此可将这两个阴影部分补上，采用方波来近似计算两桥有功能量的分配。

图12 一个工频周期内的两桥调制波形Fig.12 Modulation waveforms of the two H bridges in one power frequency cycle

4 仿真与实验

4.1 仿真

首先分析调制策略的正确性。本文基于Matlab/ Simulink首先搭建了主电路和调制电路的仿真模型，不包含控制回路，级联型整流器交流侧不接电源。桥1的直流侧接170V的直流电源，桥2的直流侧接230V的直流电源。ucon的调制波是幅值为310V、频率为50Hz的正弦交流电压。

ucon与is同号时交流侧电压仿真波形如图13所示，u1、u2的波形为按照图8中的调制波形输出的PWM波。ucon的波形由u1、u2叠加合成，但因两桥直流母线电压不相等，ucon的0电平电压并不为零，有一个偏移量，偏移量的大小为两桥直流母线电压之差。因而ucon的波形不是标准的5电平阶梯波，有一定畸变。

ucon与is异号时交流侧电压仿真波形如图14所示，u1、u2的波形为按照图9中的调制波形输出的PWM波。ucon也为畸变的5电平阶梯波，因两桥调制波形与ucon、is同号时有所差异，ucon的波形与图13中的有所不同，但因这两个ucon的调制波形是相同的，所以其基波分量是一样的。

图13ucon与is同号时的交流侧电压仿真波形Fig.13 Simulation waveforms of the AC side voltages whenuconandisare the same sign

图14ucon与is异号时的交流侧电压仿真波形Fig.14 Simulation waveforms of the AC side voltages whenuconandisare the opposite sign

由上面的分析可以看出，两桥交流侧电压的仿真波形与文中图8和图9中的调制波形是一致的，因而证明了文中对两桥调制波形的分析是正确的。

为进一步分析本文所推导出的负载平衡度限制范围的正确性，按照图3所示的控制框图搭建了具有完整控制回路的Matlab/Simulink仿真模型，仿真模型的电路参数见表3。

表3 电路参数Tab.3 Circuit parameters

开始时R1为22Ω，在5s时突变为23Ω，R2始终保持为100Ω，可以算出R1突变前后的负载平衡度分别为0.22和0.23。两桥直流母线电压仿真波形如图15所示。5s前两桥直流母线电压不能保持平衡，此时的负载平衡度小于系统的临界负载平衡度；5s后两桥直流母线电压能够恢复平衡，此时的负载平衡度大于临界负载平衡度。因此可以看出，该仿真模型的临界负载平衡度位于0.22～0.23区间。将仿真模型的电路参数代入式（11）可得临界负载平衡度的计算值为0.222。由于计算临界负载平衡度时忽略了系统损耗、谐波和调制波形畸变等的影响，计算值与仿真结果不可能完全相等。但由以上仿真结果可以看出两者非常接近，因而证明了本文的计算方法是正确的。

图15 两桥直流母线电压仿真波形Fig.15 Simulation waveforms of the DC bus voltages of two bridges

4.2 实验

为进一步验证本文所推导出的负载平衡度限制范围的正确性，搭建了基于RT-lab的半实物实时仿真实验平台。RT-lab是由加拿大Opal-RT Technologies推出的一套工业级的系统平台，在该平台上可以实现工程项目的设计、实时仿真、快速原型与硬件在回路测试。通过这种开放、可扩展的实时平台，可以实现在最短时间内、用最少花费达到验证工程的目的。为便于实验结果与仿真结果进行对比，两者的电路参数保持一致，实验平台电路参数见表3。

开始时两桥负载分别为R1=22Ω、R2=100Ω。系统稳态运行后，在t时刻切换负载，保持R2为100Ω不变，R1突变为23Ω。负载突变前后的负载平衡度分别为0.22和0.23，与Matlab/Simulink仿真模型一致。负载突变前后的两桥直流母线电压实验波形如图16所示，与图15中的仿真结果相一致，t时刻前两桥直流母线电压不能保持平衡，t时刻后两桥直流母线电压能够恢复平衡。因此可以看出，该实验平台临界负载平衡度的实际值也是位于0.22～0.23区间，与临界负载平衡度的计算值0.222非常接近。实验结果与仿真结果是一致的，进一步证明了本文的计算方法是正确的。

图16 两桥直流母线电压实验波形Fig.16 Experimental waveforms of the DC bus voltages of two bridges

负载突变前两桥交流侧的电压波形如图17所示，为按照图12中的调制波形输出的PWM波。因为此时桥2的调制波形的峰值始终小于udc2，桥1的调制波形并未出现类似三角形的小缺口，桥1交流侧电压是完整的方波。负载突变后系统达到稳态时的两桥交流侧电压波形如图18所示，此时两桥直流母线电压已恢复平衡。在某些时刻两桥直流母线电压是相等的，此时平分曲线参与调制，两桥输出占空比相等的PWM波。

图17 负载突变前的两桥交流侧电压Fig.17 AC side voltages of the two bridges before load change

图18 负载突变后的两桥交流侧电压Fig.18 AC side voltages of the two bridges after load change

负载突变前ucon与is的波形分别如图19和图20所示。由于两桥直流母线电压不平衡，ucon的波形不是标准的5电平阶梯波，与图13中的类似，有一定的畸变。对此时的is进行频谱分析，其谐波含量为6.40%。

图19 负载突变前ucon的波形及频谱分析Fig.19 Waveform and spectrum ofuconbefore load change

图20 负载突变前is的波形及频谱分析Fig.20 Waveform and spectrum ofisbefore load change

负载突变后系统达到稳态时ucon与is的波形分别如图21和图22所示，ucon为标准的5电平阶梯波。此时is的谐波含量为5.96%，与图19和图20的运行状态相比，系统电流的谐波含量有所减少。因而证明了上文中的分析与结论是正确的。

图21 负载突变后ucon的波形及频谱分析Fig.21 Waveform and spectrum ofuconafter load change

图22 负载突变后is的波形及频谱分析Fig.22 Waveform and spectrum ofisafter load change

5 结论

作为无工频变压器级联式功率变换器的输入部分，级联型整流器的稳定、可靠工作是整个变换器稳定工作的基础。受后级电路的影响，级联型整流器运行时各桥的输出功率可能存在差异，本文主要研究了这种输出功率的不平衡对于直流侧电压平衡控制的影响。首先将这种输出功率的不平衡等效为各桥直流侧连接不平衡负载。然后深入分析了两桥调制波形，并根据输入功率和输出功率的平衡关系推导出能够使两桥直流侧电压保证平衡的负载平衡度限制范围。最后通过仿真和实验验证了文中对于调制波形的分析和负载平衡度的计算是正确的。

[1] 顾春阳, 李永东, 郑泽东, 等. 多绕组高频变压器隔离式多电平变换器研究[J]. 电工技术学报, 2014, 29(8): 97-102. Gu Chunyang, Li Yongdong, Zheng Zedong, et a1. Research on a high frequency multi-winding transformer isolated multilevel converter[J]. Transactions of China Electrotechnical Society, 2014, 29(8): 97-102.

[2] Marzoughi A, Iman-Eini H. Indirect control for cascaded H-bridge rectifiers with unequal loads[C]// 2012 3rd Power Electronics and Drive Systems Technology (PEDSTC 2012), Tchran, Iran, 2012: 92-97.

[3] 李继华, 阮新波, 王学华. 级联型多电平逆变器线电压谐波优化的SVPWM策略[J]. 电工技术学报, 2014, 29(6): 120-128. Li Jihua, Ruan Xinbo, Wang Xuehua. A SVPWM strategy with optimal line-to-line voltage harmonic spectrum for cascaded multilevel inverters[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 120-128.

[4] 郑泽东, 顾春阳, 李永东, 等. 采用多绕组高频变压器的新型多电平变换器拓扑及控制策略[J]. 电工技术学报, 2014, 29(10): 12-18. Zheng Zedong, Gu Chunyang, Li Yongdong, et al. Topology and control method of a novel multi-level converter with multi-winding high-frequency transformer[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 12-18.

[5] 林志勇, 江道灼, 周月宾, 等. 基于级联H桥换流器的APF-STATCOM的控制与调制[J]. 电力系统保护与控制, 2014, 42(7): 91-96. Lin Zhiyong, Jiang Daozhuo, Zhou Yuebin, et al. Control and modulation for APF-STATCOM based on cascaded H-bridge converter[J]. Power System Protection and Control, 2014, 42(7): 91-96.

[6] 王聪, 张国澎, 王俊, 等. 一种适用于级联H桥整流直流侧电容电压快速平衡的新型调制方法[J].电工技术学报, 2013, 28(8): 120-127. Wang Cong, Zhang Guopeng, Wang Jun, et a1. A novel modulation method for fast balancing DC-link capacitor voltages of cascaded H-bridge rectifier[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 120-127.

[7] 郑征, 李斌, 胡丹丹. 基于二维调制的级联型H桥PWM整流器电压平衡控制策略[J]. 河南理工大学学报(自然科学版), 2013, 32(2): 199-204. Zheng Zheng, Li Bin, Hu Dandan. Voltage balancing control strategy for cascaded H-bridge PWM rectifier based on two dimensional modulation[J]. Journal of Henan Polytechnic University (Natural Science), 2013, 32(2): 199-204.

[8] Iman-Eini H, Farhangi S, Schanen J L. A modular AC/DC rectifier based on cascaded H-bridge rectifier[C]//13th International Power Electronics and Motion Control Conference (EPE-PEMC 2008), Poznan, 2008: 173-180.

[9] 刘文亚, 姚钢, 何娈, 等. 基于级联多电平的有源滤波器直流侧电压平衡控制[J]. 电力系统保护与控制, 2015, 43(4): 94-101. Liu Wenya, Yao Gang, He Luan, et al. Research of DC voltage balance control based on multi-level cascaded APF[J]. Power System Protection and Control, 2015, 43(4): 94-101.

[10] Wang Cong, Zhang Guopeng, Cheng Hong, et al. A novel modulation strategy based on two dimensional modulation for balancing DC-link capacitor voltages of cascaded H-bridges rectifier[C]//IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, 2012: 116-122.

[11] Zhang Guopeng, Cheng Hong, Wang Cong, et al. The voltage balance control for new generation of high power cascaded H-bridge rectifier[C]//2011 6th IEEE Conference on Industrial Electronics and Applications (ICIEA), Beijing, 2011: 1387-1391.

[12] 张兴, 张崇巍. PWM整流器及其控制[M]. 北京:机械工业出版社, 2012.

[13] 侯兆然. 基于虚拟磁链定向的PWM整流器控制方法研究[J]. 电力系统保护与控制, 2014, 42(21): 105-109. Hou Zhaoran. Research on control method of PWM rectifier based on virtual flux orientation[J]. Power System Protection and Control, 2014, 42(21): 105-109.

Load Balancing Limits of Cascaded Rectifier Based on Two-Dimensional Modulation

Zheng Zheng Li Shaoling
（School of Electrical Engineering and Automation He’nan Polytechnic University Jiaozuo 454000 China）

The loads of cascaded rectifier may be unbalanced at runtime. The DC bus voltages will fail to keep balance when the load balancing degree is beyond a certain range. In this case, the harmonic components of the AC side voltage will increase, leading to the increasing of current harmonic components accordingly. In this paper, the control method based on two-dimensional modulation is studied. Then the modulation waveforms of single-phase two-H-bridge cascaded rectifier are analyzed deeply, and the load balancing limits in which the DC bus voltages are balanceable are deduced from the modulation waveforms. A simulation model based on Matlab/Simulink and a semi-physical real-time simulation platform based on RT-lab are built up. The simulation and experimental results have verified the correctness of the analysis and the conclusion, providing a theoretical basis for the design of transformerless cascaded converter.

Cascaded rectifier, load balancing limits, two-dimensional modulation, voltage balance

TM461

郑 征 女，1965年生，博士，教授，博士生导师，研究方向为电力电子与电力传动。

E-mail: zhengzh@hpu.edu.cn（通信作者）

李绍令 男，1990年生，硕士研究生，研究方向为电力电子与电力传动。

E-mail: lylishaoling@163.com

国家自然科学基金（61340015、61340014）和河南理工大学博士基金（B2012-108）资助项目。

2014-10-14 改稿日期 2015-03-31