一种无谐波检测的三相并网逆变器谐波灵活控制方法

黄 媛罗 安王逸超

（1. 湖南大学国家电能变换与控制工程技术研究中心 长沙 410082 2. 湖南科技大学信息与电气工程学院 湘潭 411201）

一种无谐波检测的三相并网逆变器谐波灵活控制方法

黄 媛1,2罗 安1王逸超1

（1. 湖南大学国家电能变换与控制工程技术研究中心 长沙 410082 2. 湖南科技大学信息与电气工程学院 湘潭 411201）

为了简化三相并网逆变器的谐波补偿控制，同时提高并网逆变器对电网背景谐波电压的抗干扰性能，提出一种无谐波检测的三相并网逆变器谐波灵活控制方法，该方法将本地谐波补偿和抗电网背景谐波电压扰动在三相并网逆变器控制中予以统一考虑。所提控制方法可根据控制目标的不同，在谐波抑制和谐波补偿两种模式下灵活切换。谐波补偿模式，在不需要进行谐波电流检测的前提下，可实现对本地负载谐波电流的有效补偿，简化了谐波补偿时并网逆变器的控制操作；谐波抑制模式，可抑制电网背景谐波电压对逆变器输出电流的负面影响，从而提高并网逆变器的抗干扰能力。通过对同步旋转坐标系下控制器到静止坐标系的等效变换，建立了整个控制系统在静止坐标系的频域模型，分析了系统的频域跟踪特性和稳定性。仿真与实验结果证明了所提方法的有效性。

并网逆变器 谐波补偿 谐波检测 同步旋转坐标系 电网背景谐波

0 引言

近年来，可再生能源在我国能源结构中占据的比重不断上升，基于可再生能源的分布式发电技术受到了广泛应用[1-4]。并网逆变器是连接可再生能源和电网的纽带，由于可再生能源受天气、环境等因素影响，具有随机性和不稳定性，导致逆变器容量利用率低。另外，随着电力电子技术的发展，大量非线性负荷加入到电力系统中，使得电网的电能质量严重下降。因此，开发并网逆变器的电能质量补偿功能是提高并网逆变器运行效率和电网电能质量的有效手段[5-8]。

有源滤波器是补偿非线性电流的重要设备[9,10]，由于并网逆变器和有源滤波器具有相似的拓扑结构，集成有源滤波功能的并网复合控制策略成为研究热点。文献[11]分析了具有电能质量补偿功能的光伏并网系统，采用滞环控制作为电流跟踪策略。文献[12]提出一种基于同步旋转坐标系下比例积分控制器加准谐振控制器的光伏发电和有源滤波器系统。文献[13]中光伏并网逆变器采用重复控制来实现向电网输送功率和有源滤波功能。虽然上述文献采用不同的电流跟踪控制策略，但为了有效补偿本地负载中的非线性分量，都需要对本地负载中的谐波成分进行检测，尽管当前的谐波检测方法有很多种，如瞬时无功理论法[14]、离散傅里叶变换法[15]等，但都会不可避免地增加控制器运算负担。

在低电能质量环境下，背景谐波电压不仅影响并网逆变器正常运行时的输出电流质量，而且将影响逆变器在进行谐波补偿时的补偿效果。为了降低电网背景谐波电压对逆变器输出电流的负面影响，提高并网逆变器的抗干扰性能，文献[16,17]采用电网电压全前馈控制策略，消除电网背景谐波电压对逆变器入网电流的影响，但电网电压的全前馈控制过程需要进行微分运算，容易引入额外的谐波分量。文献[18]采用重复控制与同步坐标系下的比例积分控制相结合的电流控制策略，以提高在电网电压畸变以及非线性本地负载条件下并网电流的质量，但重复控制器存在时延的问题，从而影响系统控制器的动态响应速度。文献[19]针对单相并网系统，提出一种由比例跟踪控制器级联基于广义积分器的谐波补偿器的思路来抑制系统的背景谐波，但级联的方式可能导致基波跟踪控制和谐波抑制控制相互干扰，需要进一步探讨。

为了将谐波补偿功能引入三相并网逆变器，同时提高其抗干扰性能，本文以三相LCL型并网逆变器为研究对象，提出一种无谐波检测的三相并网逆变器谐波灵活控制方法。所提控制方法采用基波控制支路与谐波控制支路相并联的控制结构，电流跟踪控制兼具谐波检测功能，可实现无需谐波检测的谐波补偿和谐波抑制控制，避免谐波检测环节带来的控制负担和时延影响，同时抑制背景谐波电压对输出电流的负面影响。此外，本文推导了同步旋转坐标系下的控制器到静止坐标系的等效变换表达式，通过整个控制系统的频域特性分析证实了所提策略的控制优越性，最后通过仿真和实验验证了所提策略的有效性。

1 逆变器控制系统结构及工作模式分析

图1为三相并网逆变器控制系统结构图，逆变桥输出经过LCL滤波器滤除高频毛刺后连接至电网。本文所提控制方法如图1所示，图1中，i2为入网电流，iC为电容电流，iL为负载电流，If和Ih分别为基波控制支路和谐波控制支路的电流参考指令信号；ke为电流内环P控制器的比例系数，kPWM为逆变器增益；为αβ坐标系变换到dq坐标系的变换矩阵；为dq坐标系变换到αβ坐标系的变换矩阵；GPI为基波控制支路采用的控制器，G6R、G12R和G18R均为谐波控制支路采用的控制器。本文控制策略采用入网电流i2外环和电容电流iC内环相结合的双闭环结构，电容电流内环采用简单的比例控制，用以抑制LCL谐振尖峰，提高系统稳定性。电流外环由基波控制支路和谐波控制支路并联组成，采用同步旋转坐标系下不同的控制方法分别对逆变器输出电流中的基波分量和谐波分量进行独立控制。

图1 三相并网逆变器控制系统结构图Fig.1 Control system structure of three-phase grid-connected inverter

在基波同步旋转坐标系下，三相基波交流分量转换为直流量，因此，基波控制支路采用同步旋转坐标下的PI控制实现基波电流的无静差跟踪，PI控制器传递函数表示为

式中，kp、ki分别为PI控制的比例系数和积分系数。而在基波同步旋转坐标系下，n-1次谐波的三相负序交流分量和n+1次谐波的三相正序交流分量转换为n次谐波交流分量。因此，谐波控制支路采用同步旋转坐标下的n次准谐振控制来同时对输出电流中n-1次负序和n+1次正序谐波分量进行有效控制，n次准谐振控制器表示为

式中，knr、ωnc分别为n次准谐振控制器的谐振增益和截止频率，由于在三相交流系统中，n-1次背景谐波电压主要为负序分量，而n+1次背景谐波电压主要为正序分量，且主要谐波成分为5、7、11、13、17、19次。因此n可取6、12、18，分别对逆变器输出电流中的5、7次谐波，11、13次谐波和17、19次谐波进行控制，谐波控制支路结构如图1所示。根据控制目标的不同，谐波控制支路可以在两种工作模式下灵活切换，当逆变器近似满载或重载运行时，可将谐波控制支路指令信号Ih设置为零，此时逆变器工作在谐波抑制模式，可有效抑制主要次谐波频率背景谐波电压对逆变器输出电流的负面影响，输出高品质的电流。而当逆变器轻载运行时，可设置其工作在谐波补偿模式，此时，通过传感器检测到的本地负载电流可直接作为谐波控制支路的指令信号，在不需要谐波检测的前提下，实现本地负载谐波电流的有效补偿。综上所述，所提策略中谐波控制支路指令信号可以有两种选择为

下文将通过同步旋转坐标系下控制器的等效建模、控制系统建模及频域分析对所提控制策略进行详细阐述。

2 同步旋转坐标系下控制器等效变换分析

为了建立整个控制系统在静止坐标系的统一频域模型，分析系统的幅频跟踪特性，需要将同步旋转坐标系下的控制器等效变换至静止坐标系。早期的文献将同步旋转坐标系下PI控制近似等效为静止坐标系下的比例谐振控制[20]，这种等效解释了两种控制策略在旋转的正序基波频率具有相似表现的原因，但对于输入信号为其他频率，如负序基波频率，两种控制表现差异很大，难以等效。对此，文献[21]探讨了同步旋转坐标系下控制器到静止坐标系的等效变换过程，但仅推导了同步旋转坐标系下PI控制到静止坐标系的等效变换模型，当同步旋转坐标系采用其他控制器时，难以复制其结论。因此，本节将首先推导同步旋转坐标系下控制器变换到静止坐标系的通用等效模型。

同步旋转坐标系下控制器框图如图2所示，I、O分别表示输入、输出信号，Geq表示同步旋转坐标系下采用的控制器，Teq表示整个变换过程在静止坐标系下的等效变换模型，则可得

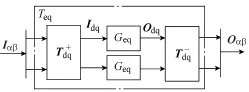
图2 同步旋转坐标系下控制器框图Fig.2 Controller diagram in dq synchronous frame

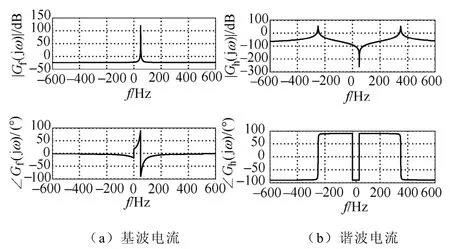
图3 基波谐波电流支路幅频和相频特性曲线Fig.3 The amplitude and phase characteristics of fundamental current and harmonic current control branch

为了简化分析，本文主要考虑对5、7次谐波进行控制，取n=6，其他次谐波的分析同理可得。取kp=0.3，ki=30，k6r=15，ω6c=4rad/s得到等效模型Gf和G6h的幅频和相频特性曲线如图3所示。在图3a中，与比例谐振控制在正负序基波频率均具有无穷大增益的表现相差异，等效模型Gf仅在正序基波频率处具有无穷大增益，而在其他频率处的增益较小。在图3b中，等效传递模型G6h仅在5次负序频率和7次正序频率处具有高增益，而在其他频率处的增益较小。因此，利用基波控制支路和谐波控制支路的频率选择特性，可分别对各自输入信号中的基波分量和谐波分量进行独立控制，相互间耦合很小。

3 所提策略的闭环模型分析

将图1中的基波和谐波控制支路分别用本文推导出的静止坐标系下的等效变换模型Gf和G6h替换，则可得到简化的双闭环电流跟踪控制框图如图4所示。

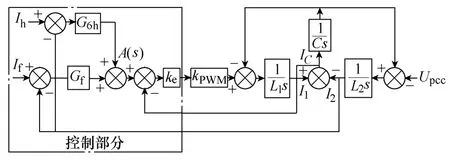
图4 双闭环电流跟踪控制框图Fig.4 Double closed-loop current control block

图4中，将电流外环输出信号A(s)和公共母线电压Upcc作为输入，则逆变器输出电流可表示为

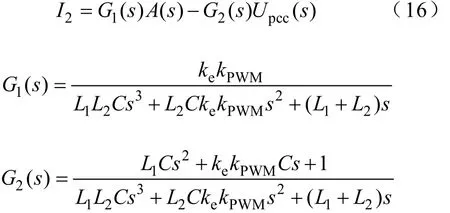
式中，G1(s)和G2(s)分别为A(s)和Upcc的闭环传递函数。电流外环输出信号A(s)可表示为

根据式（16）和式（17），可得

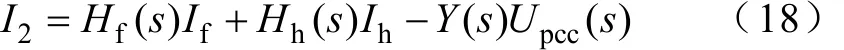
式中，Hf(s)为逆变器基波控制支路指令信号对逆变器输出电流的闭环传递函数；Hh(s)为谐波控制支路指令信号对逆变器输出电流的闭环传递函数；Y(s)为并网逆变器对电网电压的等效并联导纳，三者依次表示为

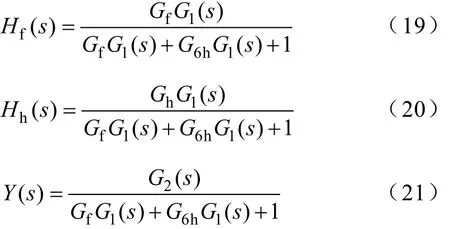
采用电流控制的逆变器可以等效为受控电流源和电阻的并联诺顿等效电路，根据式（18）可得逆变器的等效电路如图5所示，其中HfIf负责控制输出电流中的基波分量，HhIh负责控制输出电流中的5、7次谐波分量。

图5 逆变器等效电路Fig.5 Equivalent circuit of inverter

为了进一步分析逆变器的电流跟踪特性，系统参数和控制参数见表1，可以得到Hf(s)、Hh(s)和Y(s)的幅频和相频特性曲线如图6～图8所示。

图6Hf(s)的幅频和相频特性曲线Fig.6 The amplitude and phase characteristics curves ofHf(s)

通过同步旋转坐标系下控制器到静止坐标系的等效变换模型，还可以开展系统的稳定性能分析，根据式（19）～式（21）所示系统闭环传递函数可得系统的开环传递函数Gopen(s)为

图7Hh(s)的幅频和相频特性曲线Fig.7 The amplitude and phase characteristics curves ofHh(s)

图8Y(s)的幅频和相频特性曲线Fig.8 The amplitude and phase characteristics curves ofY(s)

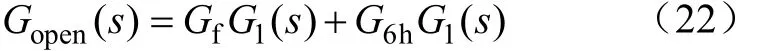
由式（22）可以得到系统的开环传递函数幅频和相频特性曲线如图9所示，在图9中，当|Gopen(s)|=0时，正序域对应的相位稳定裕度为63°，负序域对应的相位稳定裕度为61°，尽管系统在正、负序域的相位稳定裕度不一致，但均满足相位稳定裕度大于45°，系统稳定性能良好。

4 仿真及实验

利用PSIM9.0仿真软件搭建一台额定容量为6kV·A的三相并网逆变器来验证本文所提出的控制策略的有效性，采用直流侧稳压源模拟分布式电源，直流侧电压维持在700V。通过基于同步旋转坐标系的锁相环技术[22]来获取公共母线电压的基波相位sinθPLL。系统参数设置见表1。逆变器的基波控制支路指令信号由常数k乘以电网电压基波同步相位sinθPLL得到。

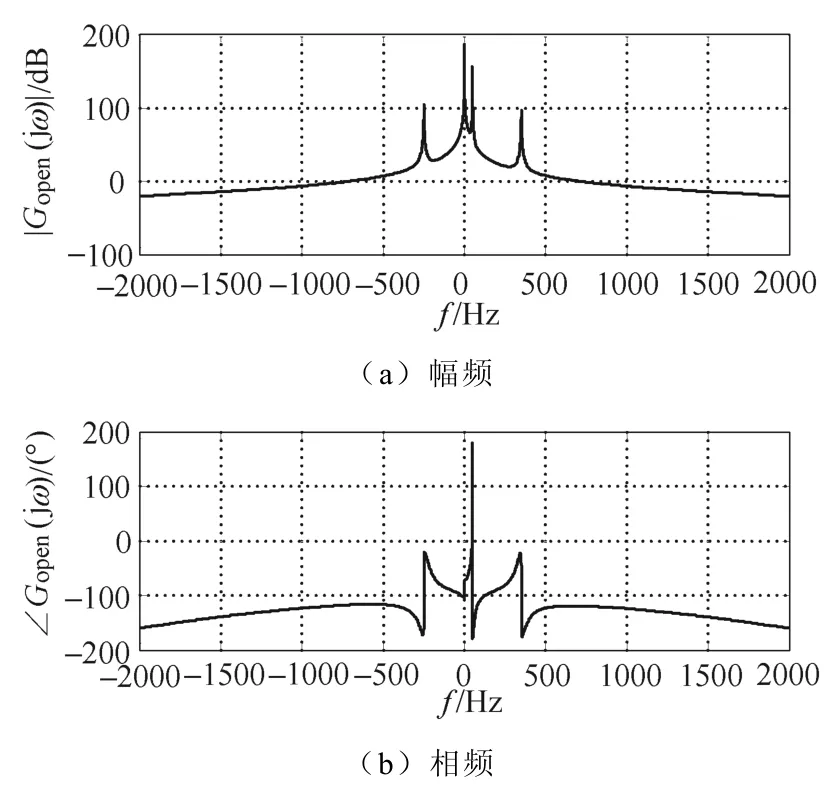
图9 系统开环传递函数幅频和相频特性曲线Fig.9 The amplitude and phase characteristics curves ofGopen(s)

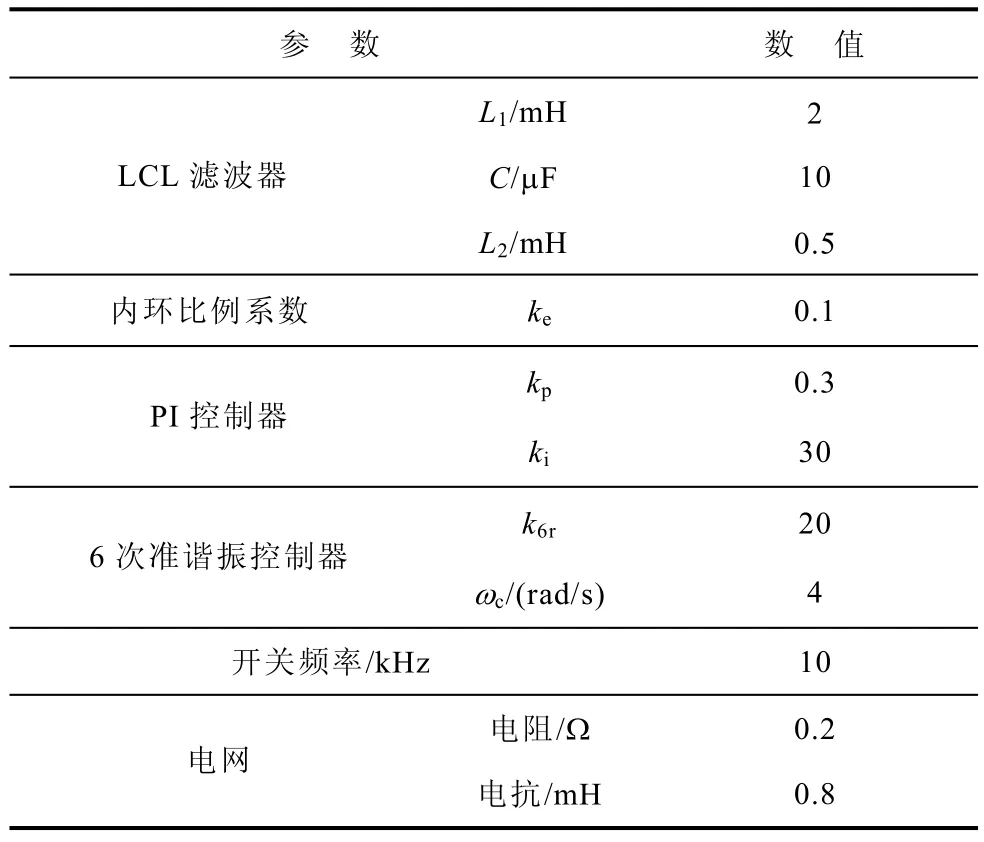
表1 系统参数Tab.1 System parameters

仿真中，由理想谐波电流源来模拟本地非线性负载，其中5次谐波电流源幅值设定为10A，7次谐波电流源幅值设定为7A。本地线性负载由阻感负载组成，其中电阻20Ω，电感30mH。

图10为k=12时，逆变器工作在近似满载时的运行仿真波形，此时谐波控制支路指令信号Ih设置为零。图10中ua、ub、uc分别为逆变器并网连接点电压，i2a、i2b、i2c分别为逆变器的三相输出电流，iga、igb、igc分别为网侧三相电流。受本地非线性负载影响，网侧电流和公共并网点电压畸变严重。但在谐波抑制模式下，逆变器对背景谐波呈现高阻态，输出高品质的电流，确保低电能质量环境下逆变器不会因为谐波过载而损坏，此时逆变器输出电流总畸变率仅为1.3%。

图10 谐波抑制模式下的仿真结果Fig.10 Simulation results under harmonic rejection mode

图11为k=3时，逆变器工作在轻载时的运行仿真波形，此时为了提高逆变器的运行效率，可将传感器检测到本地负载电流直接作为谐波控制支路的输入指令信号，使逆变器运行在谐波补偿模式。从图11中可见，在谐波补偿模式下，逆变器可以高效补偿本地负载电流中的谐波分量，从而有效降低网侧电流和公共母线电压波形畸变率，提高电网的电能质量。通过逆变器谐波补偿后，网侧电流畸变率下降至2.98%。图12为谐波补偿模式下逆变器a相输出电流的频谱分析结果，其中逆变器输出电流中的基波分量幅值3A，5次谐波电流分量幅值9.83A，7次谐波电流分量幅值6.93A。可知，逆变器输出电流中的基波分量仅受基波支路指令信号If控制，而逆变器输出电流中的谐波分量与谐波支路指令信号Ih中的谐波分量相关联，验证了在不需要谐波检测的前提下，所提控制策略依然可以实现有效的谐波补偿控制。

图11 谐波补偿模式下的仿真结果Fig.11 Simulation results under harmonic compensation mode

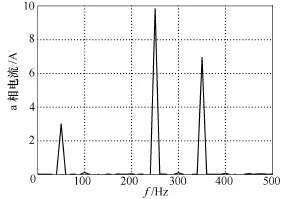
图12 谐波补偿模式下a相电流频谱Fig.12 a-phase current spectrum under harmonic compensation mode

本文在实验室搭建的三相并网发电逆变器上进一步验证所提策略的有效性，由储能装置经升压电路维持直流侧电压的稳定，逆变器最大输出功率设定为6kV·A，LCL滤波器参数及控制参数见表1。通过有源滤波装置发出5、7次固定谐波电流来模拟非线性负载，其中5次谐波电流源输出幅值8A，7次谐波电流源输出幅值6A，本地线性负载由20Ω电阻负载构成。

图13为逆变器运行在谐波抑制模式下的实验波形，其中k=10，在谐波抑制模式下，逆变器对5、7次谐波呈现高阻态，逆变器输出电流中几乎不含5、7次谐波成分，输出正弦波电流波形（见图13a），迫使非线性负载电流向网侧流入，导致网侧电流和公共母线电压畸变严重（见图13b）。

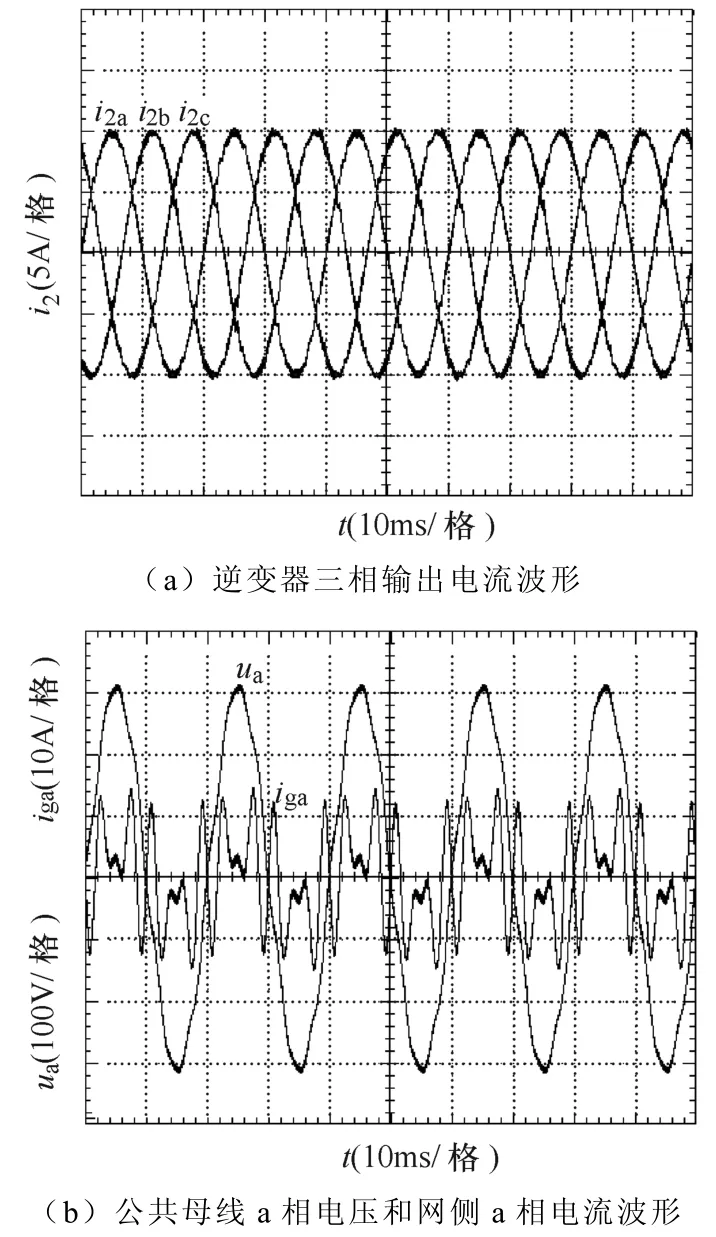
图13 谐波抑制模式下的实验结果Fig.13 Experimental results under harmonic rejection mode

逆变器运行在谐波补偿模式下的实验波形如图14所示，有源滤波装置在初始阶段正常运行，之后从电网切除，此时k=5。图14a为逆变器a相输出电流波形，图14b为a相网侧电流和公共母线电压波形。从图14中可见，在初始阶段，当负载电流中存在5、7次谐波电流时，逆变器的输出电流中的谐波分量自动跟踪负载电流中的5、7次谐波成分变化，补偿非线性负载电流，减少电网电压畸变率，改善电网电能质量。而当有源滤波装置从电网中切除后，此时负载电流中的谐波分量为零，并网逆变器仅输出幅值5A的基波电流，而不受负载电流中的基波分量影响，进一步验证本文所提策略在不需要谐波电流检测前提下，可以实现良好的谐波电流跟踪控制。

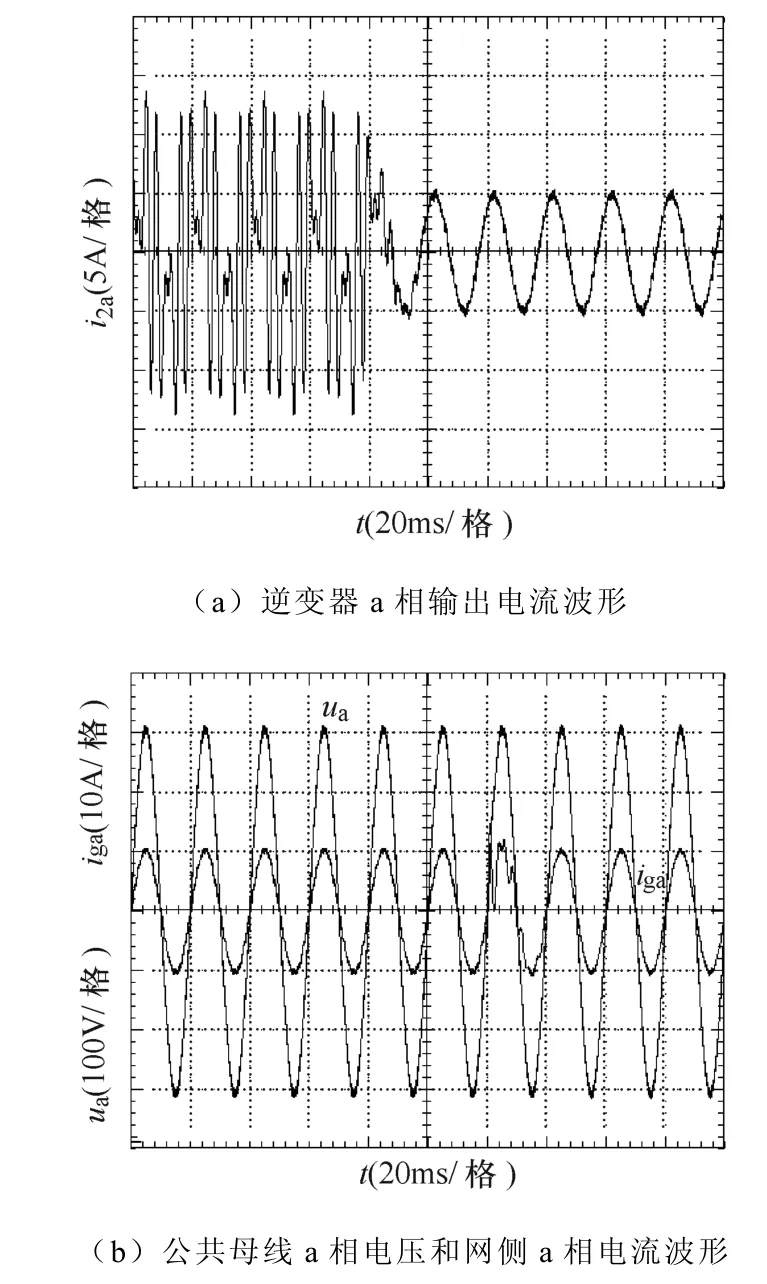
图14 谐波补偿模式下的实验结果Fig.14 Experimental results under harmonic compensation mode

5 结论

本文对三相并网逆变器谐波控制方法展开了研究，得出以下结论。

1）提出了一种无谐波检测的三相并网逆变器谐波灵活控制方法。所提控制方法可根据控制目标的不同，在谐波抑制和谐波补偿两种模式下灵活切换。谐波补偿模式下，在不需要进行谐波电流检测的前提下，可实现对本地负载谐波电流的有效补偿，简化了谐波补偿时并网逆变器的控制操作。谐波抑制模式下，可抑制电网背景谐波电压对逆变器输出电流的负面影响，从而提高并网逆变器抗干扰能力。

2）探讨了同步旋转坐标系下的控制器到静止坐标系的通用等效变换模型，相比传统等效变换模型，本文所提模型可以正确反映不同频率输入信号的控制表现，具有一定理论价值。

3）通过仿真和实验验证了本文所提控制方法的有效性。

[1] Dugan R C, McDermott T E. Distributed generation[J]. IEEE Industry Applications Magazine, 2002, 8(2): 19-25.

[2] Carley S. Distributed generation: an empirical analysis of primary motivators[J]. Energy Policy, 2009, 37(5): 48-59.

[3] 王成山, 武震, 李鹏. 微电网关键技术研究[J]. 电工技术学报, 2014, 29(2): 1-12. Wang Chengshan, Wu Zhen, Li Peng. Research on key technologies of microgrid[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 1-12.

[4] 沈鑫, 曹敏. 分布式电源并网对于配电网的影响研究[J]. 电工技术学报, 2015, 30(1): 346-351. Shen Xin, Cao Min. Research on the influence of distributed power grid for disribution network[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 346-351.

[5] He Jinwei, Li Yunwei, Shirajum M. A flexible harmonic control approach through voltage-controlled DG-Grid interfacing converters[J]. IEEE Transactions on Industrial Electronics, 2012, 59(1): 444-455.

[6] 杜春水, 张承慧, 刘鑫正, 等. 带有源电力滤波功能的三相光伏并网发电系统控制策略[J]. 电工技术学报, 2010, 25(9): 163-169. Du Chunshui, Zhang Chenghui, Liu Xinzheng, et al. Control strategy on the three-phase grid-connected photovoltaic generation system with shunt active power filter[J]. Transactions of China Electro-technical Society, 2010, 25(9): 163-169.

[7] 周念成, 楼晓轩, 王强钢, 等. 电网电压不平衡下三相光伏发电系统的谐波电流抑制[J]. 电工技术学报, 2015, 30(16): 246-254. Zhou Niancheng, Lou Xiaoxuan, Wang Qianggang, et al. Harmonic current suppression for three-phase photovoltaic power generation system under unbalanced grid voltage conditions[J]. Transactions of China Electrotechnical Society, 2015, 30(16): 246-254.

[8] 张力, 任小永, 阮新波. 基于虚拟阻抗且提高系统带宽的抑制两级式逆变器中二次谐波电流的控制策略[J]. 电工技术学报, 2014, 29(6): 136-144. Zhang Li, Ren Xiaoyong, Ruan Xinbo. Control strategy to improve the bandwidth and reduce the second harmonic current in the two-stage inverter based on virtual impedance[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 136-144.

[9] 张宸宇, 梅军, 郑建勇, 等. 基于内置重复控制器改进无差拍的有源滤波器双滞环控制方法[J]. 电工技术学报, 2015, 30(22): 125-132. Zhang Chenyu, Mei Jun, Zheng Jianyong, et al. Active power filter double hysteresis method with improved deadbeat control based on built-in repetitive controller[J]. Transactions of China Electrotechnical Society, 2015, 30(22): 125-132.

[10] 赵辉, 吕新亚, 王红君. 基于复合控制策略的混合有源滤波器谐波治理研究[J]. 电力系统保护与控制, 2015, 43(21): 60-66. Zhao Hui, Lü Xinya, Wang Hongjun. Study on control strategy based on compound control for hybrid active power filter harmonic governance[J]. Power System Protection and Control, 2015, 43(21): 60-66.

[11] Singh M, Khadkikar V, Chandra A, et al. Grid interconnection of renewable energy sources at the distribution level with power-quality improvement features[J]. IEEE Transactions on Power Delivery, 2011, 26(1): 307-315.

[12] 耿乙文, 伍小杰, 周德佳, 等. 基于改进型比例谐振控制器的三相四线制光伏发电和有源滤波器系统[J]. 电工技术学报, 2013, 28(8): 142-148. Geng Yiwen, Wu Xiaojie, Zhou Dejia, et al. Research on three phase four wire PV-AF system based on improved proportional resonant controllers[J]. Transactions of China Electrotechnical Society, 2013, 28(8): 142-148.

[13] 吴春华, 黄建明, 陈卫民, 等. 单相光伏并网与有源滤波的统一控制[J]. 电工技术学报, 2011, 26(10): 103-109. Wu Chunhua, Huang Jianming, Chen Weimin, et al. Unified control of single phase photovoltaic gridconnected and active power filter[J]. Transactions of China Electrotechnical Society, 2011, 26(10): 103-109.

[14] 王兆安, 杨君, 刘进军. 谐波抑制和无功功率补偿[M]. 北京: 机械工业出版社, 1998.

[15] 罗安. 电网谐波治理和无功补偿技术及装备[M].北京: 中国电力出版社, 2006.

[16] 吴云亚, 谢少军, 阚加荣, 等. 逆变器侧电流反馈的LCL并网逆变器电网电压前馈控制策略[J]. 中国电机工程学报, 2013, 33(6): 54-60. Wu Yunya, Xie Shaojun, Kan Jiarong, et al. A full grid voltage feed-forward control strategy with inverter-side current feedback for LCL gridconnected inverters[J]. Proceedings of the CSEE, 2013, 33(6): 54-60.

[17] 王学华, 阮新波, 刘尚伟. 抑制电网背景谐波影响的并网逆变器控制策略[J]. 中国电机工程学报, 2011, 31(6): 7-14. Wang Xuehua, Ruan Xinbo, Liu Shangwei. Control strategy for grid-connected inverter to suppress current distortion effected by background harmonics in grid voltage[J]. Proceedings of the CSEE, 2011, 31(6): 7-14.

[18] 郭小强, 邬伟扬, 漆汉宏. 电网电压畸变不平衡情况下三相光伏并网逆变器控制策略[J]. 中国电机工程学报, 2013, 33(3): 22-28. Guo Xiaoqiang, Wu Weiyang, Qi Hanhong. Control strategies for three-phase PV grid-connected inverter under distorted and unbalanced voltage conditions[J]. Proceedings of the CSEE, 2013, 33(3): 22-28.

[19] 刘波, 杨旭, 孔繁麟, 等. 三相光伏并网逆变器控制策略[J]. 电工技术学报, 2012, 27(8): 64-70. Liu Bo, Yang Xu, Kong Fanlin, et al. Control strategy study for three phase photovoltaic grid-connected inverters[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 64-70.

[20] Zmood D N, Holmes D G. Stationary frame currentregulation of PWM inverters with zero steady-state error[J]. IEEE Transactions on Power Electronics, 2003, 18(3): 814-822.

[21] Zou Changyue, Liu Bangyin, Duan Shanxu, et al. Stationary frame equivalent model of proportionalintegral controller in dq synchronous frame[J]. IEEE Transactions on Power Electronics, 2014, 29(9): 4461-4465.

[22] Kaura V, Blasko V. Operation of a phase locked loop system under distorted utility conditions[J]. IEEE Transactions on Industry Application, 1997, 33(1): 58-63.

A Flexible Harmonic Control Method for Three-Phase Grid-Connected Inverter without Harmonic Detection

Huang Yuan1,2Luo An1Wang Yichao1
（1. National Electric Power Conversion and Control Engineering Technology Research Center Hunan University Changsha 410082 China 2. College of Information and Electrical Engineering Hunan University of Science and Technology Xiangtan 411201 China）

In order to simplify the harmonic compensation control and improve anti-interference ability to grid background harmonic voltage, a flexible harmonics control method for three-phase grid-connected inverter without harmonic detection is proposed. Herein, the local harmonic current compensation and the resistivity against grid background harmonic voltage disturbances are considered together in the controller. The proposed control method can switch between harmonic suppression mode and harmonic compensation mode depending on control targets. In the harmonic compensation mode, this method can achieve effective compensation for local load harmonic current without harmonic current detection. It will simplify the control operation of grid-connected inverter in case of harmonic compensation. In the harmonic suppression mode, this method can suppress the negative impacts of grid background harmonic voltage on the output current of the inverter, so as to improve anti-jamming capability of the inverter. By the equivalent transformation of controller from synchronous rotating reference frame to stationary reference frame, the frequency-domain model of the entire control systemin stationary reference system has been established. The frequency-domain tracking characteristics and system stability have been analyzed. The simulation and experimental results have demonstrated the effectiveness of the proposed method.

Grid-connected inverters, harmonic compensation, harmonic detection, synchronous rotating reference frame, grid background harmonic

TM464

黄 媛 女，1981年生，博士研究生，讲师，研究方向为微电网运行与控制及电力有源滤波。

E-mail: hy_8615381@163.com（通信作者）

罗 安 男，1957年生，教授，博士生导师，研究方向为电力有源滤波、无功补偿以及微电网控制。

E-mail: an_luo@hnu.edu.cn

国家自然科学基金重点项目（51237003）和国家高技术研究发展计划（863计划）（2011AA05A301）资助。

2015-07-28 改稿日期 2015-10-19