基于多电平逆变器的感应加热双频率输出设计

冷朝霞 刘庆丰

（西安理工大学自动化与信息工程学院 西安 710048）

基于多电平逆变器的感应加热双频率输出设计

冷朝霞 刘庆丰

（西安理工大学自动化与信息工程学院 西安 710048）

为了提高双频率感应加热设备的电源利用率，对基于多电平技术的双频感应加热的电压输出问题进行了研究。采用阶梯波近似模拟所需双频信号的合成波形，依据近似波形构造逆变器的输出电压波形。利用输出波形的傅里叶展开式，建立以逆变器触发延迟角为自变量的频率信号幅值方程。基于方程的求解结果，对所构造的输出电压信号和相同电平数的常规多电平信号进行基波调制系数及3次谐波调节范围的对比分析、所构造的输出电压信号具有更大的谐波调节范围。采用二极管钳位H桥逆变器拓扑，设计了实现所构造电压信号的逆变器触发方式，并兼顾考虑了逆变器分压电容的电压均衡问题。逆变器的仿真与实验结果验证了所提逆变器触发方式的有效性及对所构造信号计算分析的正确性。

感应加热 二极管钳位逆变器 双频率输出 谐波调节范围 触发方式

0 引言

感应加热装置是利用电磁感应原理，通过感应线圈将电能转化为热能的设备，已被应用于许多工业领域，如透热、熔炼、热处理和焊接等[1-3]。已有的研究表明，感应线圈中的电流频率是决定工件加热性能的重要因素。由于电流频率的二次方根与工件的加热厚度（透入深度）成反比，频率影响感应电流的大小及工件的升温速度。因此，在处理表面几何形状不规则的加热工件时，仅用单一频率的感应电流对不同部分的处理效果将不一致，严重影响工件的处理质量。如在汽车及航空工业领域应用广泛的复杂工件齿轮、大宽厚比板状件的硬化处理。由于受不同部位加热厚度及角度半径的影响，常规的单频率感应加热技术难以满足这类材料的热处理要求，易造成工件变形、烧蚀等缺陷。

为解决复杂几何表面工件的热处理问题，近年来国内外已有一些双频感应加热的方法被提出。文献[4]基于单频率感应加热原理，采用两台感应加热电源、两个感应线圈和一个高速机械转换器组合实现双频感应加热，但存在结构庞大、操作复杂，且由于工件的分时、分别处理造成硬化效果不均衡等问题。同步双频（Simultaneous Dual Frequency, SDF）感应加热技术，是在一个感应线圈上同时使用两种不同频率对一个工件进行处理，该方法由德国ELDEC公司与HANVOER大学及ILMANO大学、意大利PADUA大学共同研制。文献[5-8]基于SDF技术，采取双逆变器结构实现双频率信号的输出，但它在技术实现中存在以下缺陷：①双逆变器控制方式复杂，同步实现困难；②两逆变器功率耗散不均衡；③电磁干扰现象严重，由于采用了非理想的谐振电路，输出频率信号的准确性将受到影响。日本学者K. Matsuse和S. Okudaira近年来一直致力于研究双频率感应加热电源[9-13]，提出的主要技术思路是带短路开关的准谐振逆变器结构，这种方案存在感应线圈电流断续、谐振频率分时变化和加热过程间断的缺陷。西班牙学者V. Esteve等提出了单个逆变器和一组四元件复合谐振电路的双频率感应加热拓扑结构[4,6,14,15]，但两个谐振频率点的功率等级、频率等级相差较大且无法单独调节。

基频和三倍频双频感应加热电源适用于超音频高频感应加热场合，如凸轮、曲轴、花键轴及大模数齿轮的淬火[16]，金属材料的双频电磁成形处理等[17,18]。以往的单逆变器双频率感应加热电源的研究主要是通过谐振电路的设计提高负载槽路的双频信号选择能力，本文以输出基频和三倍频信号为例，对双频率信号的构建、产生及信号特性进行了描述。为了改善单逆变器结构感应加热电源的同步双频率信号输出性能，从信号构成的角度，研究提高逆变器输出双频率信号能力的问题。提出根据所需信号频率构建逆变器输出电压波形的方法，基于多电平技术，分析对比了相同电平数不同电压波形的信号特性，从而确定了逆变器相应的工作方式。

1 双频率信号构建方法

设需产生的双频率信号的频率分别为f1和f2，根据信号叠加方法，将式（1）所示的两个频率分别为f1和f2的正弦信号s1、s2同相位相加，根据信号叠加后的波形特征，确定能产生所需双频率信号（f1和f2）的阶梯波波形。

式中，f2=mf1，m为奇数；A1、A2表示信号的幅值。

信号叠加时保证低频率f1为基波频率，即叠加后的合成信号具有和信号s1相同的过零点。

图1展示了m=3时两个正弦信号在一个周期内的合成结果及其近似阶梯波波形，实线表示基频信号与三倍频率信号的合成曲线，虚线表示近似合成曲线的阶梯波。

图1 两信号合成结果及其近似阶梯波Fig.1 The synthesis result of two signal and the approximate step waveforms

对阶梯波信号进行傅里叶分解，求出所需两频率分量的幅值表达式，利用Matlab平台进行数值求解，分析两频率分量的可调节范围。

根据阶梯波的电平数，设计多电平逆变电路及触发方法，实现阶梯波的输出。

下面以实现基频与三倍频双频率信号为例，对双频率信号的构建过程进行详细说明。

2 基频与三倍频双频率信号构建

首先按照图1的方式设计产生双频率信号的阶梯波波形，为了增加波形可调节的变量维数，将图1中的阶梯波改造为图2所示的带零电平的S波形，用变量θ1、θ2表示电平变化时对应的角度，E为直流输入电压，图2的阶梯波即为构造的双频感应加热逆变器的输出电压信号。

图2 双频感应加热逆变器的输出电压Fig.2 The output voltage of dual-frequency induction heating inverter

2.1 双频率信号特性分析

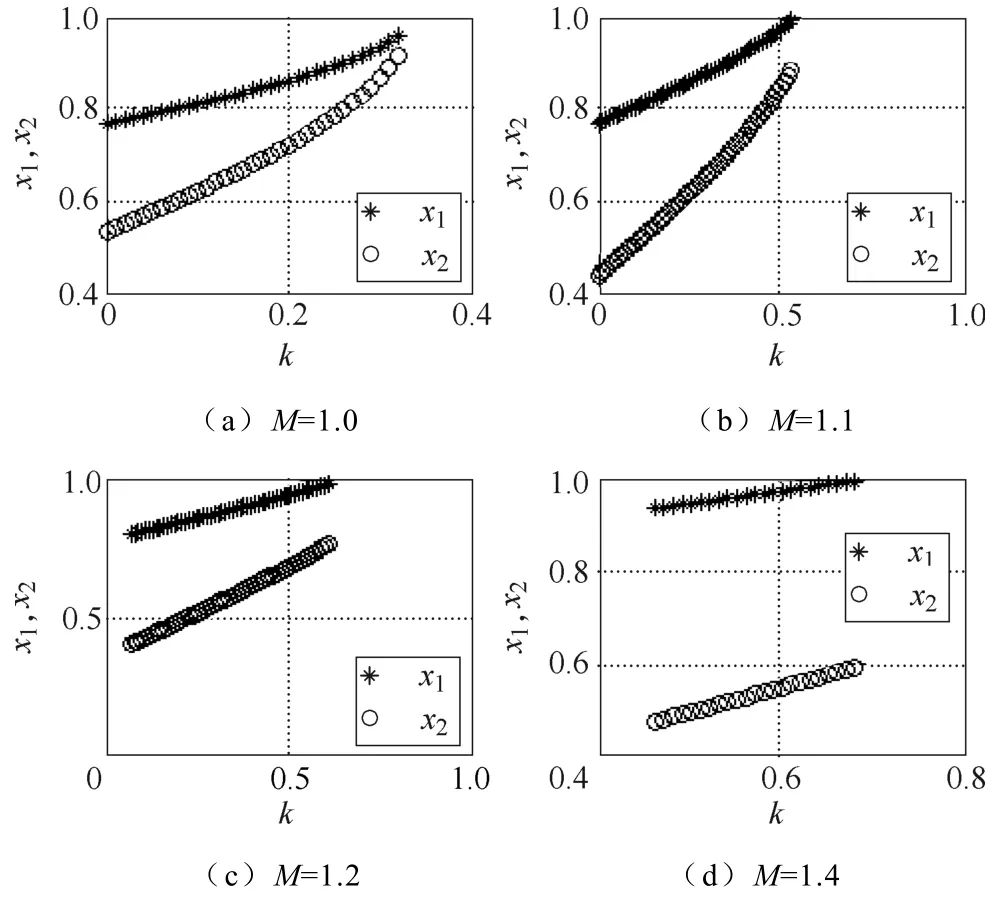
图3M=1.0, 1.1, 1.2, 1.4时k、x1、x2的取值关系Fig.3x1,x2versuskwith differentM=1,1.1,1.2,1.4

根据式（7）中的第二组解，由图4提供了基波调制系数M=1.4, 1.6, 1.7, 1.8时，k、x1、x2的取值关系。

图4M=1.4, 1.6, 1.7, 1.8时k、x1、x2的取值关系Fig.4x1,x2versuskwith differentM=1.4,1.6,1.7,1.8

为突出图2所构造的多电平信号谐波调节特性，采用相同的分析方法对图5中具有相同电平数的常规多电平信号[19-21]进行谐波特性分析计算。

图5 电平叠加的多电平信号Fig.5 Multi-level signal with superposition levels

根据计算可得

M和k的取值范围依次对应为。

图6、图7分别提供了基波调制系数M＜1和M＞1时，k、x1、x2的取值关系。

根据对比式（7）、式（8）中M和k的取值范围，并通过对比图3、图4与图6、图7的显示结果，可知在相同M条件下，图2所构造的多电平信号比相同电平数的常规多电平信号具有更大的3次谐波调节范围。

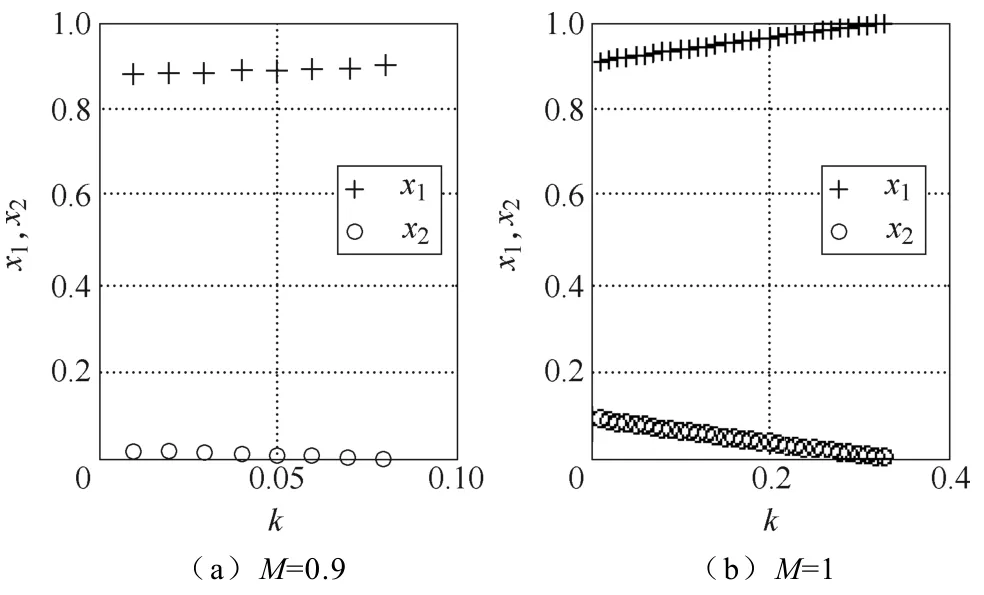
图6M＜1条件下k、x1、x2的取值关系Fig.6x1,x2versuskwhenM＜1

图7M＞1条件下k、x1、x2的取值关系Fig.7x1,x2versuskwhenM＞1

另外，2.1节的数值计算及仿真结果也说明了，通过改变θ1、θ2的值可以实现基波和3次谐波幅值的调节。

2.2 逆变器工作方式设计

采用图8所示的二极管钳位H桥逆变器实现图2所构造的双频率感应加热电压输出。图8中，Qa1～Qa4、Qb1～Qb4为功率开关器件，VD1～VD4为钳位二极管，C1、C2为分压电容，E为逆变器直流输入，功率开关Qa1、Qa3，Qa2、Qa4，Qb1、Qb3以及Qb2、Qb4的驱动脉冲都是互补的，同一桥臂上每两个功率器件同时处于导通或关断状态，每对功率器件遵循先关断后开通的原则。

二极管钳位型逆变器可选择多种开关组合来实现图2中的输出电压，为改善分压电容C1、C2的电压均衡问题，逆变器采用如图9所示的开关触发方式工作，图9中依次给出了Qa1～Qa4、Qb1～Qb4的触发信号。θ1、θ2代表开关器件的触发延迟角。

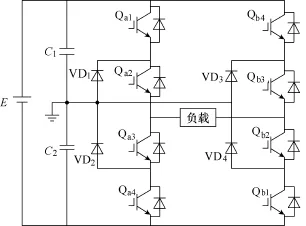
图8 二极管钳位H桥逆变器拓扑Fig.8 Diode-clamped H-bridge inverter

图9 触发信号Fig.9 Driving signal

为保证逆变器良好的工作状态，感应加热电压型逆变器应工作在弱感性状态，即逆变器输出电流稍滞后于输出电压α电角度[3]。根据图9的工作方式及逆变器弱感性的工作特点，每个工作周期，逆变器经历10个工作模态，各模态的电路如图10所示。

模态1：-θ1～θ1区间，开关器件Qb3、Qa3与二极管VD2、VD3导通，逆变器输出零电压，其工作电路如图10a所示，iload为负载槽路电流。

模态2：θ1～θ1+α区间，α为逆变器输出电流滞后于输出电压的角度。逆变器输出电流通过开关器件Qb1、Qb2、Qa2、Qa1的极间反并联二极管续流，逆变器输出电压E，此时电压已换相，输出电流未换相，其工作电路如图10b所示。

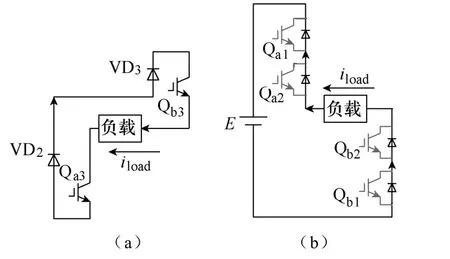
图10 各模态电路Fig.10 The circuit of each mode

模态3：θ1+α～θ2区间，开关器件Qa1、Qa2、Qb2、Qb1导通，逆变器输出电压E，输出电流换相，其工作电路如图10c所示。

模态4：θ2～π-θ2区间，开关器件Qa1、Qa2、Qb2与二极管VD4导通，电容C1放电，C2充电，逆变器输出电压E/2，其工作电路如图10d所示。模态4中，电容C1的电压降低，设其变化量为ΔVC1；电容C2的电压增加，设其变化量为ΔVC2且ΔVC1=-ΔVC2。

式中，f为逆变器开关频率。

模态5：π-θ2～π-θ1区间，模态5重复模态3的逆变器运行状态，逆变器输出电压E，其工作电路如图10c所示。

模态6：π-θ1～π+θ1区间，开关器件Qa2、Qb2和二极管VD4、VD1导通，逆变器输出零电压，其工作电路示意图如图10e所示。

模态7：π+θ1～π+θ1+α区间，逆变器输出电流通过开关器件Qa4、Qa3、Qb3、Qb4的极间反并联二极管续流，逆变器输出电压-E，电压已换相，输出电流未换相，其工作电路如图10f所示。

模态8：π+θ1+α～π+θ2区间，开关器件Qb4、Qb3、Qa3、Qa4导通，逆变器输出电压-E，输出电流换相，其工作电路如图10g所示。

模态9：π+θ2～2π-θ2区间，二极管VD3与开关器件Qb3、Qa3、Qa4导通，电容C1充电，C2放电，逆变器输出电压-E/2，其工作电路如图10h所示。模态9中，电容C1的电压增加ΔVC1。电容C2的电压降低ΔVC2，ΔVC1=-ΔVC2，电容C1、C2的电压变化计算如式（9）所示。

模态10：2π-θ2～2π-θ1区间，模态10重复模态8的逆变器运行状态，逆变器输出电压-E，其工作电路如图10g所示。

根据以上对逆变器10个工作模态的运行分析可知，分压电容C1、C2只在模态4和模态9中有电荷运动。在模态4中，电容C1放电，C2充电，C1的电压减少值和C2的电压增加值分别与模态9中C1的电压增加值和C2的电压减少值相等。因此，逆变器按照图9的触发方式工作，在一个工作周期中，分压电容C1、C2能实现良好的电压均衡。

图11给出了逆变器按照图9的触发方式工作时，逆变器输出电压波形和分压电容C1、C2的电压波形。图11中Vo为逆变器输出电压，VC1、VC2分别为电容C1、C2的电压。

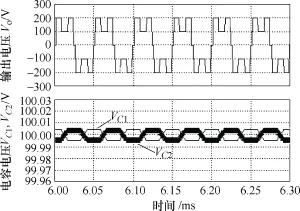
图11 均衡电容电压波形Fig.11 The balanced voltage waveforms of capacitances

不同的触发信号如图12所示。为了对比研究，图13给出了逆变器按照不同于图9的触发方式（见图12）工作时，逆变器输出电压波形及电容电压波形。图12的触发中改变了Qa2、Qa4、Qb2、Qb4的触发信号。

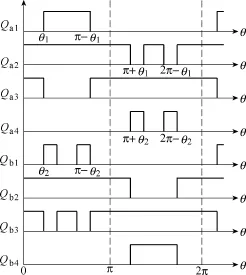
图12 不同的触发信号Fig.12 The different driving signal

图11中，采用图8的逆变器拓扑及图9的触发方式，可以实现图2所构造的双频率感应加热电压输出。并且通过与图13的结果对比可知，逆变器采取不同触发方式工作，输出相同电压时，采用本文提出的工作方式（见图9），能改善分压电容电压的均衡问题。

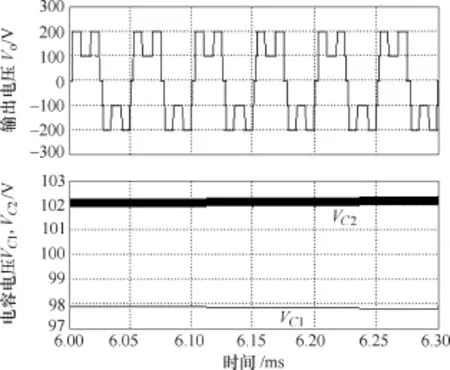
图13 不均衡电容电压波形Fig.13 The unbalanced voltage waveforms of capacitances

3 仿真与实验

采用PSIM进行电子线路仿真，逆变器采用图8所示的结构，直流电压E=200V，开关频率f= 20kHz，分压电容C1=C2=10mF。

图14为逆变器触发延迟角设置为θ1=10°，θ2=62°时的逆变器输出电压波形及其Fourier波形，根据式（3）、式（4）计算，x1=0.984 8，x2=0.469 5，M=1.500 1，k=0.605 8。

根据图14中Fourier波形的数据可知，输出电压基波分量的幅值V1=191.47V，3次谐波分量的幅值V3=115.79V，经计算可得M=1.503，k=0.604 7。仿真结果与根据式（3）、式（4）计算的结果近似相等。

图14 当θ1=10°，θ2=62°时的逆变器输出电压仿真波形Fig.14 The simulation waveforms of inverter output voltage withθ1=10°,θ2=62°

图15为逆变器触发延迟角设置为θ1=25°，θ2=72°时的逆变器输出电压波形及其Fourier波形，根据式（3）、式（4）计算，x1=0.906 3，x2=0.309，M=1.503 6，k=0.294 1。

图15 当θ1=25°，θ2=72°时的逆变器输出电压仿真波形Fig.15 The simulation waveforms of inverter output voltage withθ1=25°,θ2=72°

根据图15中Fourier波形的数据可知，输出电压基波分量的幅值V1=189.889V，3次谐波分量的幅值V3=57.083V，经计算可得M=1.491 4，k=0.300 6。仿真结果与根据式（3）、式（4）计算的结果稍有偏差，稍许偏差是由于仿真中功率器件存在开通、关断过程，造成输出电压在器件开关期间中存在上升、下降的过程。

图14与图15的仿真结果说明，通过控制逆变器触发延迟角θ1、θ2，可以实现在几乎不改变基波幅值的情况下，实现3次谐波幅值的调节。因为k=0.3是图5中常规多电平信号具有的3次谐波最大可调节上限，因此图14与图15的仿真结果也表明，逆变器输出本文所构造的多电平输出电压（如图2所示），能扩大逆变器输出电压的3次谐波调节范围。

图16为逆变器触发延迟角设置为θ1=19°，θ2=47°时的逆变器输出电压波形及其Fourier波形，根据式（3）、式（4）计算得到x1=0.945 5，x2=0.682，M=1.209，k=0.514 6。

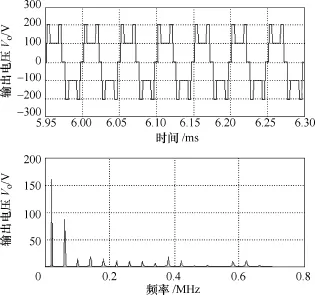
图16 当θ1=19°，θ2=47°时的逆变器输出电压仿真波形Fig.16 The simulation waveforms of inverter output voltage withθ1=19°,θ2=47°

根据图16中Fourier波形的数据可知，输出电压基波分量的幅值V1=156.78V，3次谐波分量的幅值V3=84.94V，经计算可得M=1.231 3，k=0.541 8。仿真结果与根据式（3）、式（4）计算的结果也稍有一些偏差，原因同图15的说明相同。

由图16的仿真结果说明，通过控制逆变器触发延迟角θ1、θ2，实现了输出电压基波幅值的调节，而且与图7的仿真结果中M=1.2对比可知，在相同的基波幅值情况下，相对于图5所示的常规多电平信号，本文所构造的多电平输出电压具有更大的3次谐波调节范围。

实验参数设置与仿真参数一致，电压信号采用霍尔传感器采集，控制器采用TMS320F28335，功率器件采用FF300R12KS4，DSP的输出信号通过光耦加载到开关管的驱动。

图17为θ1=10°，θ2=62°时逆变器输出电压及其Fourier的实验波形，输出电压基波分量的幅值V1= 192V，3次谐波分量的幅值V3=118.4V，经计算可得M=1.507 2，k=0.616 7。

图17θ1=10°，θ2=62°时逆变器输出电压实验波形Fig.17 The experimental waveforms of inverter output voltage withθ1=10°,θ2=62°

图18为逆变器分压电容C1、C2的电压实验波形。图18显示，每个分压电容在一个周期内充、放电一次，充、放电电荷几乎相同。两个分压电容的电压相差22mV，可近似认为实现了均压。

图18 分压电容电压实验波形Fig.18 The experimental waveforms of the partial-voltage capacitances

图19为θ1=25°，θ2=72°时逆变器输出电压及其Fourier的实验波形，输出电压基波分量的幅值V1=191.8V，3次谐波分量的幅值V3=55.4V，经计算可得M=1.506 4，k=0.288 8。

图20为θ1=19°，θ2=47°时逆变器输出电压及其Fourier的实验波形，输出电压基波分量的幅值V1=153.6V，3次谐波分量的幅值V3=79V，经计算可得M=1.206 4，k=0.514 3。

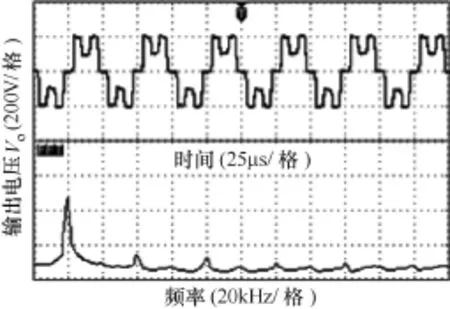
图19θ1=25°，θ2=72°时逆变器输出电压实验波形Fig.19 The experimental waveforms of inverter output voltage withθ1=25°,θ2=72°

图20θ1=19°，θ2=47°时逆变器输出电压实验波形Fig.20 The experimental waveforms of inverter output voltage withθ1=19°,θ2=47°

仿真与实验结果说明，通过控制逆变器触发延迟角θ1、θ2，实现了输出电压基波幅值、3次谐波幅值的调节，而且与图7的仿真结果对比可知，在相同的基波幅值情况下，本文所构造的多电平输出电压具有更大的3次谐波调节范围。

4 结论

本文以适于凸齿等元件淬火处理及金属材料双频电磁成形的超音频高频电源为应用背景，以提高感应加热单逆变器输出双频率信号的能力为目的，以产生基频和三倍频双频输出电压为例，论述了根据所需信号频率构建逆变器输出电压的方法。通过计算分析确定了所构建的电压波形具有比相同电平数的常规多电平信号更大的谐波调节范围。

本文提出的根据所需信号频率进行逆变器输出电压的分析、设计方法，可用于其他双频信号的构建及分析。

本文的研究工作旨在从提高逆变器双频信号输出能力方面为单逆变器同步双频感应加热电源奠定一定的研究基础，控制策略等方面的研究将作为后续工作逐步展开。

[1] 李时峰, 吕默影, 陈辉明. 一种新型超高频感应加热混合全桥逆变器[J]. 电工技术学报, 2013, 28(3): 215-221. Li Shifeng, Lü Moying, Chen Huiming. A novelhybrid full-bridge inverter for ultra-high frequency induction heating applications[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 215-221.

[2] 孙于, 汪友华, 杨晓光, 等. 新型横向磁通感应加热线圈[J]. 电工技术学报, 2014, 29(4): 85-90. Su Yun, Wang Youhua, Yang Xiaoguang, et al. A novel coil shape for transverse flux induction heating[J]. Transactions of China Electrotechnical Society, 2014, 29(4): 85-90.

[3] 刘庆丰, 王华民, 冷朝霞, 等. 基于多电平逆变器的高频感应加热电源若干问题的研究[J]. 电工技术学报, 2007, 22(6): 82-88. Liu Qingfeng, Wang Huamin, Leng Zhaoxia, et al. A study on several problems for high frequency induction heating power supply based on multilevel inverter[J]. Transactions of China Electrotechnical Society, 2007, 22(6): 82-88.

[4] Esteve V, Pardo J, Jordán J, et al. High power resonant inverter with simultaneous dual-frequency output[C]//IEEE 36th Power Electronics Specialists Conference, Recife, 2005: 1278-1281.

[5] Esteve V, Jordán J, Dede E J, et al. Induction heating inverter with simultaneous dual-frequency output[C]// Applied Power Electronics Conference And Exposition, Dallas, 2006: 1505-1509.

[6] Schwenk W, Peter H J. Applications for surface induction hardening using SDF induction heat treating[J]. Elektrowärme International, 2002(1): 13-18.

[7] Oscar Lucía, Pascal Maussion, Dede E J, et al. Induction heating technology and its applications: past developments, current technology, and future challenges[J]. IEEE Transactions on Industrial Electronics, 2014, 61(5): 2509-2520.

[8] 王娅琦, 周伟松, 赵前哲. 同步双频感应加热电源的研究[J]. 电力电子技术, 2013, 47(1): 18-20. Wang Yaqi, Zhou Weisong, Zhao Qianzhe. Study of synchronous dual-frequency induetion heating power suppIy[J]. Power Eleetronies, 2013, 47(1): 18-20.

[9] Matsuse K, Okudaira S. Power control of an adjustable frequency quasi-resonant inverter for dual frequency induction heating[C]//Power Electronics and Motion Control Conference, Beijing, 2000: 968-973.

[10] Okudaira S, Matsuse K. Dual frequency output quasi-resonant inverter for induction heating[J]. Transactions Institute of Electrical Engineers of Japan, 2001, 121(5): 563-568.

[11] Matsuse K, Okudaira S. A new quasi-resonant inverter with two-way short-circuit switch across a resonant capacitor[C]//Proceedings of the Power Conversion Conference, Osaka, 2002: 1496-1501.

[12] Okudaira S, Matsuse K. New quasi-resonant inverter with shortcircuit switches across the resonant capacitor and its operating characteristics[J]. Transactions of the Institute of Electrical Engineers of Japan, 2005, 125(8): 793-799.

[13] Okudaira S, Matsuse K. Adjustable frequency quasi-resonant inverter circuits having short-circuit switch across resonant capacitor[J]. IEEE Transactions on Power Electronics, 2008, 23(4): 1830-1838.

[14] 何婷, 周伟松, 赵前哲. 单逆变桥同步双频感应加热电源的研究[J]. 电力电子技术, 2013, 47(10): 84-86. He Ting, Zhou Weisong, Zhao Qianzhe. Research on simultaneous dual-frequency induetion heating power suppIy based on single inverter bridge[J]. Power Eleetronies, 2013, 47(10): 84-86.

[15] Vicente Esteve, José Jordán, Esteban Sanchis-Kilders, et al. Comparative study of a single inverter bridge for dual-frequency induction heating using Si and SiC MOSFETs[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1440-1450.

[16] 秦中平, 李英华, 闫林平, 等. 普通高频感应加热设备改为双频感应加热设备的研究[J]. 农业装备与车辆工程, 2001(3): 3-4. Qin Zhongping, Li Yinghua, Yan Linping, et al. Research on the change of common high frequency induction heating equipment to dual frequency induction heating equipment[J]. Agricultural Equipment and Vehicle Engineering, 2001(3): 3-4.

[17] 李双明, 郝启堂, 李金山, 等. 液态金属双频电磁约束成形过程研究[J]. 稀有金属材料与工程, 2001, 30(6): 418-421. Li Shuangming, Hao Qitang, Li Jinshan, et al. Dual-frequency electromagnetic shaping process of liquid metal[J]. Rare Metal Materials and Engin-eering, 2001, 30(6): 418-421.

[18] 卢百平, 沈军, 刘林, 等. 耐热不锈钢真空双频电磁约束成形[J]. 稀有金属材料与工程, 2008, 37(6): 1103-1107. Lu Baiping, Shen Jun, Liu Lin, et al. Dual-frequency electromagnetic hold shaping for heat resistant steel parts under vacuum[J]. Rare Metal Materials and Engineering, 2008, 37(6): 1103-1107.

[19] 赵志宏, 赵剑锋, 沈凯安, 等. 二极管钳位型五电平逆变器低调制比电压平衡与矢量序列的分析[J].电工技术学报, 2014, 29(6): 153-162. Zhao Zhihong, Zhao Jianfeng, Shen Kaian, et al. Analysis of voltage balancing strategy and vector sequences of a five-level diode-clamped converter[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 153-162.

[20] 王奎, 郑泽东, 李永东, 等. 基于五电平有源中点钳位型双PWM变换器的异步电机矢量控制系统[J].电工技术学报, 2014, 29(2): 247-252. Wang Kui, Zheng Zedong, Li Yongdong, et al. Vector control system for induction motors based on five-level active neutral-point-clamped dual-PWM converter[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 247-252.

[21] 李宁, 王跃, 厉肃, 等. 直流电容电压自平衡的新型五电平NPC变流器空间矢量调制策略[J]. 电工技术学报, 2015, 30(6): 177-189. Li Ning, Wang Yue, Li Su, et al. DC capacitor voltage self-balancing space vector modulation strategy of five-level NPC converter[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 177-189.

Design of Dual Frequency Output of Induction Heating Based on Multilevel Inverter

Leng Zhaoxia Liu Qingfeng
（School of Automation and Information Engineering Xi’an University of Technology Xi’an 710048 China）

In order to improve the power utilization rate of dual frequency induction heating equipment, this paper studied the voltage output problems of dual frequency induction heating based on the multilevel technology. The synthetic waveform of the dual frequency signal was approximately simulated by the step wave. And then this approximate wave form was applied to construct the output voltage waveform of the inverter. By using the Fourier expansion of the output waveform, the amplitude equations of the frequency signal were established, in which the independent variable was the trigger angle of the inverter. After that, the fundamental modulation coefficient and the three-harmonic regulation range of the constructed output voltage signal were analyzed, which were compared with the conventional multilevel signal with the same level number. The constructed output voltage signal has a larger range of harmonic regulation. The diode clamped H-bridge inverter topology was adopted. The driving mode of inverter was designed to realize the constructed voltage signal, taken into account the voltage balancing problem of the partial-voltage capacitances. The simulation and experimental results verify the proposed driving mode as well as the correctness of the calculation and analysis of the constructed voltage signal.

Induction heating, diode clamped inverter, dual frequency output, harmonic regulation range, driving mode

TM46

冷朝霞 女，1976年生，博士，讲师，研究方向为电力电子功率变换技术。

E-mail: lengzhaoxia@xaut.edu.cn（通信作者）

刘庆丰 男，1971年生，博士，副教授，研究方向为电力电子功率变换技术。

E-mail: liuqingfeng@xaut.edu.cn

2016-06-02 改稿日期 2016-07-21