浅析隔离法和整体法在高中物理解题过程中的应用
2017-01-20许卓淋
许卓淋
摘 要:如果我们想要把物理知识的基本框架结构掌握,就需要学会总结和归类物理思想的方法。通过对结构和模式的掌握,使我们更清楚地了解物理方法,从而提高自身的解题能力。我们在高中物理学习阶段常用的物理方法有整体法和隔离法,如果同学们能对这种方法熟悉掌握,准确地选择研究对象,那么在解题时就会更加简单和明了。
关键词:高中物理;整体法;隔离法;应用
一、整体法和隔离法的应用概述
物理解题中的基本方法就包括整体法和隔离法,所谓的隔离法,就是将我们所要研究的对象从它所处的物理环境中“拿出来”,单独对它研究。整体法就是将几个不同的物体当作一个整体来分析,或是将有不同特点或者性质的几个物理过程当作一个整体的过程来研究。一般情况下,关于连接体的题目,我们采用的是隔离法,当然也可以用整体法来研究。如果一个问题可以用整体又可以用隔离,那么我们优先选择整体法来研究。对于大部分的动力学问题,如果只用整体法可能很难解决,所以可以采用整体法和隔离法互相结合来研究。
二、对整体法的应用
(一)物体加速度和大小均相同
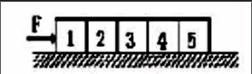
例:如下图所示,在一个光滑的水平面上有五个物体,分别是1,2,3,4,5这五个物体质量相等,都为m,此时推1号物体,且水平推力是F。求:图中物体的加速度?2号和3号物体之间压力大小?
解析:由题目我们可以知道图中物体的加速度是一样的,因为它们之间是连结的,所以我们求解时可以将五个物体看作是一个整体,进而求解整体加速度。然后对3,4,5号物体进行研究,求解出2号和3号之间的压力。首先,对整体我们可以得到:F=5ma,a=F/5m;研究3,4,5号物体我们得到:T=3ma,T=3F/5。
2、物体的加速度不相同
例:木块ABC静止在粗糙的水平面上,且M=10kg,水平面的滑动摩擦因数为u=0.02。木块倾斜的角为30度,在斜面上有一物体下滑,且物体m=1.0kg,当物体滑行的路程s=1.4m,物体速度为V=1.4m/s。木块在此过程中没有移动,求木块受地面摩擦力的方向和大小。
解析:物体m在沿着斜面下滑过程中,所受的力有重力,弹力和摩擦力。物体m的状态是不平衡的,所以M受地面摩擦力的作用,那么我们可以根据平衡条件来对此题进行求解。或者我们用整体法,将M和m看作整体来研究,运用牛顿第二定律来解题。我们得到m在下滑时的加速度为0.7m/s2,把研究对象看作是M与m,可得M受地面摩擦力:f=macos ,A=0.61N,摩擦力方向是水平向左的。
三、对隔离法的应用
对隔离法的应用我们从例子中进行分析。
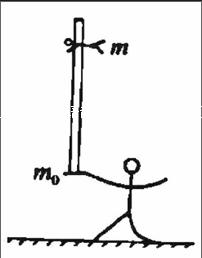
例:如下图所示是一段杂技表演,图中在地上的演员质量m1=60kg,肩上托举一根竹竿,竹竿长6m,质量为m0=5kg。此时另外一个质量为m=40kg的演员,从竹竿顶部往下滑,运动状态是先匀加速,后匀减速。当他到达竹竿底部时速度减少为0。其中演员下滑时匀加速的加速度为匀减速加速度的2倍,一共用了3S的时间。求解演员在匀加速和匀减速下滑过程中,站在地面上的演员对地面的压力大小。
解析:假设a为演员在竹竿上匀加速下滑的加速度,对题中的演员进行隔离,我们可以得到方程:at=a(3-t),t2+a(3-t)2=6,对两个方程求解得:a=4m*s-2。接着将两个演员和竹竿看作整体研究,得到演员匀加速下滑时站在地上的演员对地面压力为:FN1= (m1+mo+ m)g-ma=890N,而在匀减速阶段得到:FN2=(m1+m0+m)g+1/2ma=1130N。
四、在物理多过程中对整体法和隔离法的运用
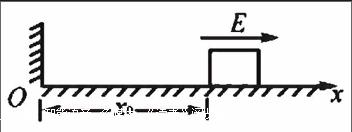
例:如图所示,图中有一向右运动物体,质量为m,所带电荷为-q,在O处有一墙壁与轨道垂直,图中场强的大小是E,其方向沿着X。此时图中物体的初速度为V0,它从X0出发,沿着OX方向运动,所受摩擦力大小不变,为f,且Eq>f,如果假设物体运动为理想运动,那么求解它停止之前所能通过的路程大小。
解析:由题目可知,Eq>f,所以只要物体不在O位置,且在X上,那么物体不受平衡力作用,所以物体最后静止时应该是靠在墙上的,也就是处于O位置,对小物体初始和最后状态进行比较,不难发现其减少了动能及电势能,根据能量守恒,损失的能量由于摩擦力作用转化成了内能我们可以得到:mV02+EqX0=fs。
五、结语
综上所述,在我们运用整体法和隔离法解决问题时,首先要根据题目来选取最为合适的方法,一般外力选整体,内力选隔离。在学习其他的物理知识时也是一样,要懂得整体和隔离相互配合,这样可以更好地帮助我们对所学力与运动的关系进行掌握,有利于我们提升自己的思维能力。
参考文献:
[1] 张任.受力分析方法的活用[J].科技创新与应用,2013(26).
