磁梯度张量定位盲点分析

邓超凡 伍东凌 陈正想

（中国船舶重工集团公司第七一〇研究所，宜昌，443003）

磁梯度张量定位盲点分析

邓超凡 伍东凌 陈正想

（中国船舶重工集团公司第七一〇研究所，宜昌，443003）

针对目前磁性目标单点磁梯度张量定位方法受地磁场影响较大的问题，通过对原算法的偏微分推导，提出了一种改进磁梯度张量定位方法，并分析了在这种算法在定位过程中可能存在的定位盲点。利用Matlab仿真验证了这种算法的可行性及探测盲点存在的位置与分析的一致性。

磁梯度张量；磁定位；探测盲点；Newton插值

磁梯度张量定位方法具有很多磁总场定位、磁矢量定位方法所没有的优点，如受磁化方向影响小、具有较多的细节能够用于三维定量反演解释等[1]，在军事、环境、资源勘探等方面有着广阔的应用前景[2]。近年来，磁梯度张量探测定位技术逐渐成为磁测技术的研究热点[3-4]。本文主要针对一种单点磁梯度张量定位算法的探测盲点进行分析，提出了一种在实际探测过程中的修正方法，并通过仿真验证了这种方法的可行性。

1 改进的探测方法

1.1 磁梯度张量定位算法

磁场是一个矢量场，其3分量Bx、By、Bz在空间3个方向的变化率即为磁梯度张量，包括9个要素，表达式为

由文献[2]推导出磁偶极子的位置信息与单点所测量的磁场矢量及磁张量之间的线性关系：

由式（2）可知，在已知某点处磁张量的九个要素及相应的磁偶极子所产生的三分量磁场值就可得到磁偶极子的位置信息，如式（3）所示：

式（3）为单点磁张量定位算法，已知单一观测点的目标磁场和磁梯度张量可实现磁性目标定位。

但是在实际测量中，目标磁场估计值B会包含地磁场的测量误差。由于地磁场的大小为几万nT，而目标磁场的大小一般为几百nT，因此在地磁场远大于目标磁场的情况下，较小的地磁场测量相对误差也会给目标磁场的估计值B带来较大影响[5]，进而给单点磁梯度张量的定位带来较大误差。

1.2 磁梯度张量定位改进算法

将式（2）写成方程组的形式，并对方程组等号两边分别对z求偏导，可得

式（4）可简化表示为

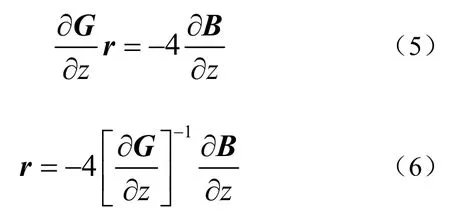
式（6）就是基于磁梯度张量定位的改进算法，由于磁体的尺寸越大，其磁场的二阶和三阶张量越小，所以地球作为一个尺寸巨大的磁体，与一般磁性目标相比，其二阶和三阶张量远小于目标磁场的二阶和三阶张量，因此地磁场对改进定位算法中变量的影响很小，所以该改进定位算法不受地磁场影响。

2 磁梯度张量探测盲点分析

对于磁梯度张量定位算法，上述理论分析都是在假设磁梯度张量对z的偏导可逆的情况下进行的。当不可逆时，在以磁偶极子为坐标原点的坐标系中的定位公式（6）是不存在的。这样使得磁梯度张量对z的偏导不可逆的奇异点称之为磁梯度张量探测定位盲点，简称探测盲点。

进一步地分析可以得出，探测盲面实际上是两个经过磁偶极子，并且垂直或平行于磁矩矢量的平面，于是当时，探测盲面在以磁偶极子为坐标原点的坐标系中的一般方程为：

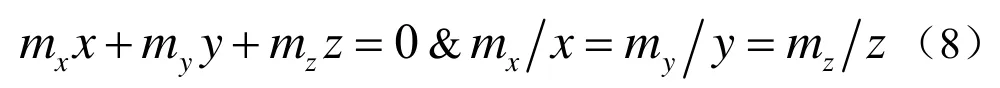
3 磁梯度张量探测盲点仿真

为了验证探测盲点或者探测盲面的存在，需要选定磁偶极子在某个位置不变，利用磁探测系统对其进行探测，此时可以建立以磁偶极子为坐标原点的坐标系，而磁探测系统在磁偶极子上方的某个平面内运动，利用公式（6）可以计算出磁探测系统相对于磁偶极子原点的位置坐标，由相对性可得磁偶极子相对于磁探测系统的位置坐标。这里在仿真时，以磁探测系统的运动位置坐标为准，即求解的是磁探测系统在以磁偶极子为原点的坐标系中的坐标。

探测盲点的仿真步骤如下：（1）选取以磁偶极子为坐标原点的坐标系，如图1所示。（2）在磁偶极子上方某一高度h处，选择一个平面为磁探测系统的运动平面。（3）将磁探测系统的运动平面进行离散化，离散点作为磁探测系统的探测位置点。（4）让磁探测系统运动到不同的位置点，利用磁探测系统对磁偶极子进行探测定位。（5）将利用定位公式所求得的探测位置坐标与真实位置坐标(x,y,z)进行比较，根据式（9）求取绝对误差。

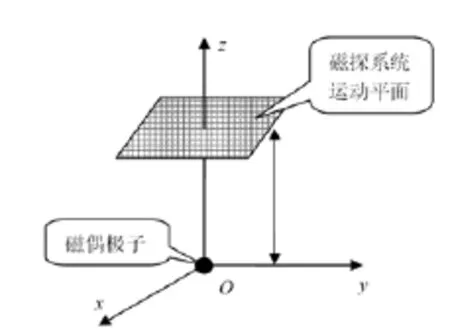
图1 仿真分析示意图

仿真过程中，假设磁偶极子的磁矩mx=100 Am2、my=0、mz=0，其他仿真条件不变，此时由探测盲面的一般方程可知，此时的探测盲面为x=0或z=0，而由于磁探测系统在磁偶极子的上方z=h平面内运动，所以探测过程中当磁探测系统位于探测盲面和运动平面的交线处时，磁探测系统对自身位置的探测误差会急剧增大。

假设h=2 m，传感器之间的排列间距d=0.5 m，坐标系X、Y方向上取−8 m到8 m。则定位计算所得到的三轴坐标值与真实值之间的误差（以Ey为例）如图2所示。

图2 磁测探系统y坐标的相对误差Ey

由图2可以看出，在探测盲面x=0和磁性目标探测系统运动平面的交线以外的区域即x≠0的区域，定位误差在0附近波动很小，而在探测盲面x=0和磁性目标探测系统运动平面的交线处确实存在定位误差急剧增大的情况，甚至在一些点上因不能对求逆而无法实现定位，在图2上显示为空白区域，这与理论分析完全吻合。从而进一步说明，磁梯度张量探测存在探测盲面，探测盲面在以磁偶极子为坐标原点的坐标系中的一般方程可由式（8）求出。

同样假设h=0 m，其他条件不变。即在z=0的平面上进行探测，则定位计算所得到的三轴坐标值与真实值之间的误差（同样的以Ey为例）如图3所示。

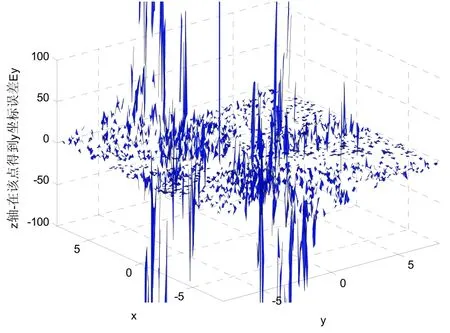
图3 磁测探系统y坐标的相对误差Ey

由图3可以看出，在探测盲面z=0的区域探测只能在一些极为零散的点上能得到定位结果，且定位误差极大，基本无法实现定位，这与上面的理论分析也是完全吻合的。从而进一步说明这种探测方法存在探测盲面，探测盲面在以磁偶极子为坐标原点的坐标系中的一般方程可由式（8）求出。所以在利用磁梯度张量探测系统对磁性目标探测定位时，需要避开探测盲面和运动平面的交线-探测盲线。避开探测盲线的方法可以利用磁探测系统之前的探测数据进行外插，或者利用最近的一组探测数据直接替换进行修正。

可采用Newton插值多项式x=0上的数据外插以替代直接通过公式（9）得到的探测结果，插值公式为：

其中

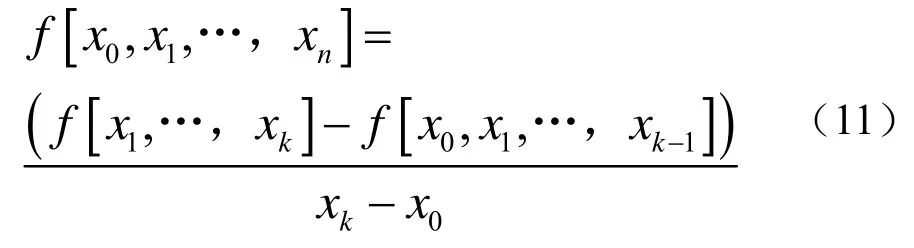
通过仿真验证这种方法的可行性，在利用外插公式（10）对x=0上的数据外插时，可取与该点坐标y相同且距离最近的4个x≠0的点上探测结果作为已知量进行外插，得到的结果替代公式（6）的探测结果。事实证明，这些方法切实可行。修正后的相对定位误差如图4～图6所示。

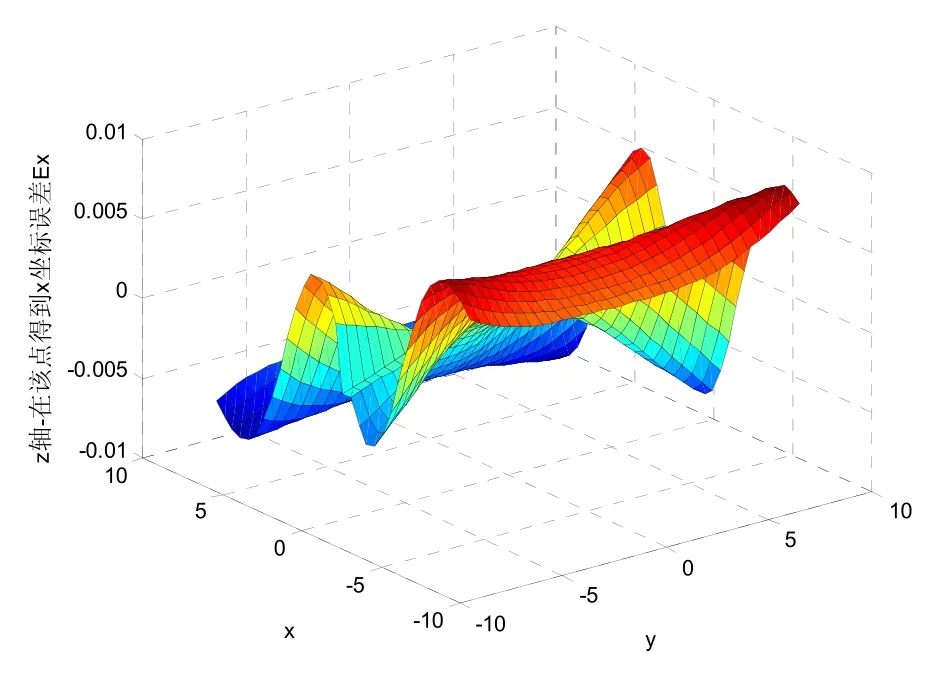
图4 修正后磁测探系统x坐标的相对误差Ex

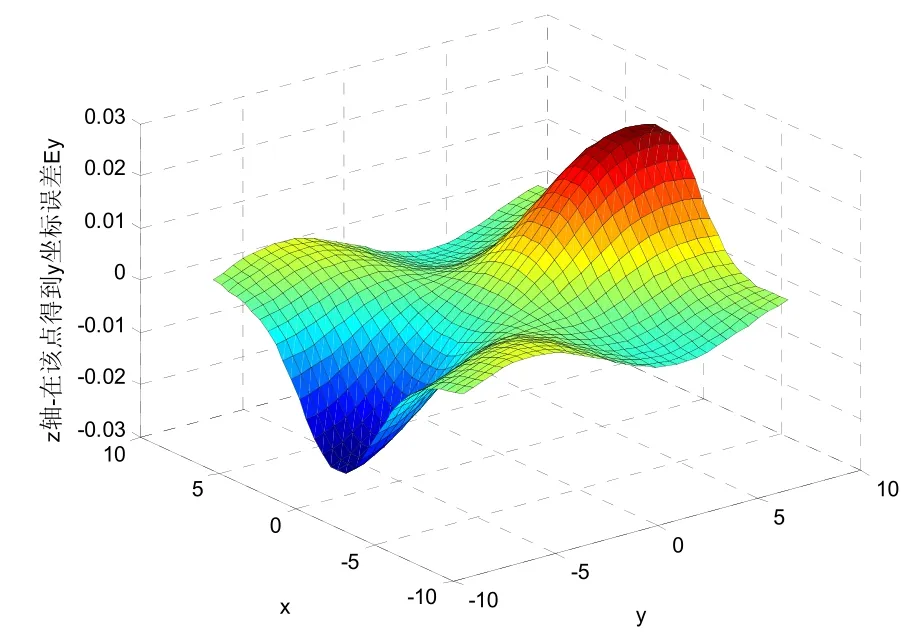
图5 修正后磁测探系统y坐标的相对误差Ey

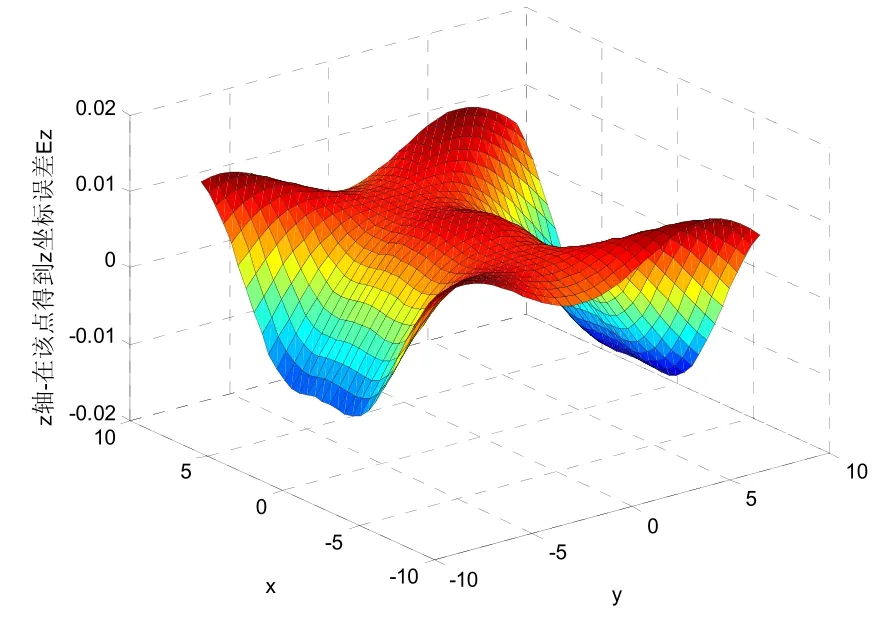
图6 修正后磁测探系统z坐标的相对误差Ez

由图4～图6可以看出，修正后探测盲点被消除，同时可以看出利用磁梯度张量探测系统进行探测定位时，对x、y、z坐标的相对定位误差小于0.03 m，可在实际工程中应用。

4 结束语

本文通过Matlab仿真，验证了改进算法在探测过程中确实有探测盲点存在，位置与前面的数学分析结果一致，即探测盲面是两个经过磁偶极子，并且垂直或平行于磁矩矢量的平面；提出了利用Newton插值法对探测结果进行修正的数据处理方法，从仿真结果可以看到修正后x、y、z坐标的相对定位误差小于0.03 m，对磁梯度张量定位在实际工程中的应用有一定的指导意义。另外，由于本文的分析和仿真都是基于理想条件下进行的，即在研究过程中没有考虑噪声的影响，在下一步的工作中可探究噪声对探测距离、精度及探测盲点位置的影响。

[1]张昌达.航空磁力梯度张量测量－航空磁测技术的最新进展[J].工程地球物理学报,2006,3(5):354-361．

[2]张朝阳，肖昌汉，闫辉．磁性目标单点梯度张量定位方法[J]．探测与控制学报，2009，31(4)：44-48.

[3]TAREK E T，AHMED S．Position detection of unexploded ordnance from airborne magnetic anomaly data using 3-D self organized feature map [J]．International Symposium Signal Processing and Information Technology，2005，23(1)：322-327．

[4]黄玉，郝燕玲．磁场梯度张量定位中的矢量磁力计最简配置[J]．华中科技大学学报(自然科学版)，2010，38(12)：52-55．

[5]于振涛，吕俊伟，樊利恒．基于磁梯度张量的目标定位改进方法[J]．系统工程与电子技术，2014，36(7)：1250-1254．