基于Copula双变量模拟的CoCo债券定价

李 平,尹菁华,来 娜,黄光东

(1.北京航空航天大学经管学院,北京100191; 2.广发证券,广东广州510075;3.中国地质大学(北京)信息学院,北京100080)

基于Copula双变量模拟的CoCo债券定价

李 平1,尹菁华2,来 娜1,黄光东3*

(1.北京航空航天大学经管学院,北京100191; 2.广发证券,广东广州510075;3.中国地质大学(北京)信息学院,北京100080)

用Copula函数刻画公司股价与核心一级资本比率(core tier 1 ratio,CTR)的相关性,然后通过模拟股价和CTR,建立了或有可转换债券(CoCo)以及带期权条款的或有可转换债券(CoCoCo)的定价模型.并将模型应用于塞浦路斯银行发行的CECS(convertible enhanced capital securities)债券,发现用Copula刻画股价与CTR相关性的定价结果与债券实际价格的差异优于假设两者独立时的结果.最后结合国际上已发行的CoCo和CoCoCo债券的相关条款以及我国银监会对于减记债的基本要求,以交通银行为例设计了中国版的CoCo债券和CoCoCo债券,并依据所给模型对它们进行了数值计算.

CoCo债券;CoCoCo债券;核心一级资本比率;Clayton Copula

1 引 言

CoCo债券是2008年次贷危机后出现的新型债券品种,主要被银行用于补充资本金,对于银行系统的稳定有重要作用.2009年以来国际上已有多家银行发行CoCo债券,如劳埃德银行集团(Lloyds BankingGroup),塞浦路斯银行(The Bank of Cyprus)和西班牙毕尔巴鄂比斯开银行(Banco Bilbao Vizcaya Argentaria)等.CoCoCo债券是在CoCo债券的基础之上增加了转换期权条款,转股价格一般高于当前股价,因此当银行经营良好时,投资者可以获得超过普通债券的收益,所以CoCoCo债券的潜在回报要高于CoCo债券.塞浦路斯银行于2011–06–02发行并于2012–12–31触发减记条款的CECS是CoCoCo债券的典型代表.

2012年以来,我国银监会先后发布了两份关于国内银行发行减记债的指导意见,允许国内银行发行减记债.从其特征来看,减记债可以看作是中国版的CoCo债券[1].根据指导意见,五大国有商业银行和兴业、光大、民生、平安等股份制银行,以及10余家城市商业银行和农村商业银行,均发行了减记型二级资本工具,发行总额超过4 200亿元.平安银行于2014年3月发行了国内首只上市交易的减记债.

由于巴塞尔委员会以及各国金融监管机构都对CoCo债券的设计提出了自己的要求,本文将把研究重点放在CoCo和CoCoCo债券的定价上.目前对CoCo债券定价的相关研究已经比较丰富.Madan等[2]在结构化定价模型的基础上使用4个相互独立的Levy过程同时对资产和负债的收益率进行模拟,更接近实际的同时也使得模型异常复杂;Barucci等[3]使用双时间段的结构化模型,对减记(writing down)前后资本构成各部分价值进行了分析;Pelger[4]在CoCo债券期限有限以及资产收益率服从跳扩散过程的假设下对CoCo债券进行了定价;Chen等[5]使用了带有两个跳跃过程的跳扩散模型,分别表示公司特有风险和市场风险;Pennacchi等[6]运用结构化模型为COERC(call option enhanced reverse convertible)这种带有看涨期权的CoCo债券进行定价.Yang等[7]给出了结构化模型下资产服从跳扩散过程时CCS(contingent convertible security)资产价值的闭式解;Spiegeleer等[8]提出了CoCo债券定价的股权衍生品模型及信用衍生品模型,将期权定价方法及信用风险度量方法应用到CoCo债券定价中;Brandt等[9]采用信用衍生品方法为CoCo债券定价,计算出CoCo债券的信用风险溢价,利用现金流折现公式得到CoCo债券的定价公式; Cheridito等[10]采用信用衍生品定价模型,假设CoCo债券触发服从时变的泊松过程,从而给出CoCo债券的定价公式,并在此基础进行CoCo债券的风险分析;Corcuera等[11]应用权益衍生品定价方法,给出了息票可取消的CoCo债券的定价公式,结果表明,息票可取消的CoCo债券可以改善Hillion等[12]认为的转换条款会带来的死亡螺旋情况;Veiteberg等[13]提出使用股价与核心一级资本比率(CTR)双变量来估计CoCo债券价格.

国内相关研究方面,王晓林等[14]针对市场的不完备性对CoCo债券进行了设计和定价,并研究了包含CoCo债券的公司最优资本结构.秦学志等[15]用债转股概率刻画CoCo债券的触发点,建立了基于不同触发点的CoCo债券的银行最优资本结构模型.秦学志等[16]利用二叉树模型给出了离散时间下或有可转债定价公式,并将其推广到连续时间情形.

由于CoCoCo债券出现得更晚,因此研究文献很少.Girolamo等[17]首次对CoCoCo债券进行了详细介绍和定量分析:在股权衍生品模型下,假设股价波动服从Heston模型,无风险利率满足Hull-White模型,然后对CoCoCo债券进行了定价.Girolamo等认为,CoCoCo债券可以给投资者向上的获利空间,对投资者的吸引力要优于普通的CoCo债券,同时可以降低银行的融资成本.

目前已有的关于CoCo和CoCoCo债券定价的研究文献存在的主要问题在于,没有恰当地度量股价与核心一级资本比率(CTR)之间的相关性.结构化模型以及股权衍生品模型均使用公司的市场价值来度量CoCo债券的价值.但是已有的CoCo债券均使用核心一级资本比率(CTR)作为减记指标,而CTR是以财务数据为基础进行计算的.于是上述三种模型就隐含了市场价值与CTR高度相关的假设,而Veiteberg[13]则假设了股价与核心资本比率相互独立,走向另一个极端.本文作者通过对国内16家上市银行股价与核心一级资本比率的相关性进行分析,发现不同银行的相关系数的绝对值从0.04到0.95不等,因此单个银行简单地假设独立或高度相关并不能反映真实情况.此外,股价与CTR独立的假设没有考虑到二者的尾部相关性问题.当危机出现时,资金会偏好资本充足率较高的更安全的银行,这会带来资本充足率指标与股价在极端事件下的正相关性.CoCo债券的设计正是为了应对这种情况的出现,因而在考虑减记概率以及CoCo债券的相关风险时不能忽略资本充足率与股价的尾部相关性.

刻画变量间尾部相关性的Copula理论在信用衍生品定价中有诸多应用.Li[18]用Copula函数刻画资产间的违约相关性;Hull等[19]运用因子Copula模型对NDS(nthto default swaps)进行定价;艾春荣等[20]将债券的流动性和违约风险及两种风险的相关性引入到公司债券定价中,并用Copula数刻画不同相关结构下公司债券的收益率和风险变化;周孝华等[21]应用Copula函数处理多元资产间的相关性;Li等[22]用动态Copula刻画了公司资产之间的动态违约相关性,然后对BDS(basket default swap)进行了定价.

本文引入Copula函数来刻画核心一级资本比率CTR与股价之间的相关性,并建立CoCo和CoCoCo债券的定价模型.在实证研究部分,用Kolmogorov-Smirnov检验进行最优Copula函数的选取.检验结果表明,Clayton Copula与经验Copula的拟合效果最好.然后用估计的参数和Clayton Copula对将来的股价和CTR进行Monte Carlo模拟,并对塞浦路斯银行发行的CoCoCo债券做实证定价检验.最后根据我国银监会的要求与金融市场的现状,以交通银行为例设计了中国版的CoCo和CoCoCo债券(即减记债),并进行数值定价计算.

2 CoCo和CoCoCo债券定价模型

2.1 核心一级资本比率(CTR)的边缘分布

Serjantov[23]以核心一级资本比率(CTR)为因变量上一期的CTR与均值的差值为自变量进行回归检验,发现二者具有显著的负相关关系,而且银行的CTR具有一定的均值回复特性.他还发现CTR的变化值的历史数据具有尖峰厚尾的特性,因此用带跳跃的Vasicek模型[24]来刻画CTR的变化率x(t)如下

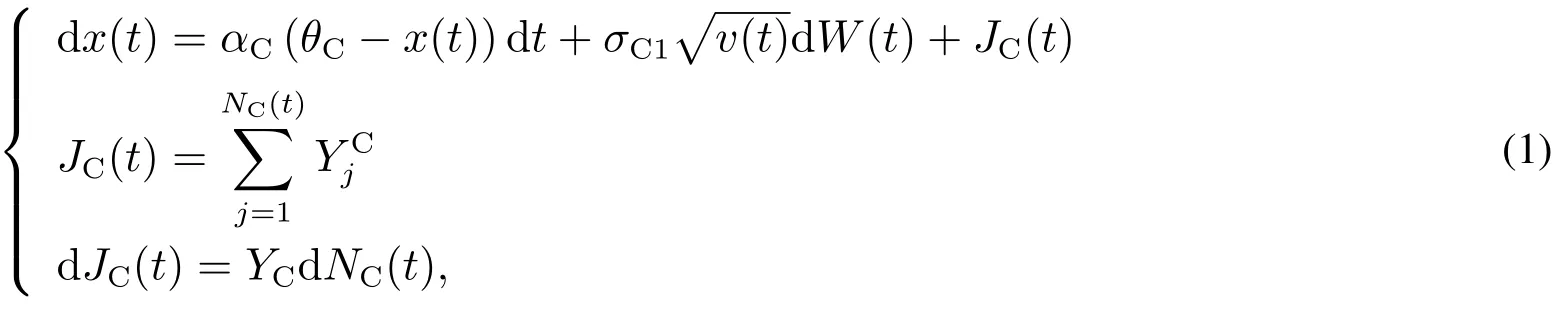
其中αC是CTR的均值回复参数,θC是CTR的目标值,σC1是x(t)的波动率,W(t)是维纳过程,JC(t)表示CTR变化率x(t)的跳跃部分,用于刻画CTR的厚尾,NC(t)是强度为λC的泊松过程,是独立同分布的随机变量.

假设在一个时间段中最多只有一次跳跃发生,即N(t)=1,并参考Ball等[25],假设在[t,t+dt]时间段中发生跳跃的概率Q=λCdt,不发生跳跃的概率为1-Q.

2.2 股价的边缘分布

刻画股价收益率分布的模型有很多,Heston[26]提出的随机波动率模型由于较好地平衡了度量误差与计算速度,在期权定价中应用广泛.为了更好地描述股价收益率厚尾的特征,本文在Heston模型中加入跳跃成分.因此,股价的变化可表示为

其中µS1与v(t)分别是股价的期望收益率和方差,z1(t)和z2(t)是相关系数为ρS的两个维纳过程,JS(t)表示股价的跳跃部分,并且z1(t)与JS(t)相互独立.这里跳跃发生的次数NS(t)是强度为λS的泊松过程,是独立同分布的随机变量;与刻画CTR的变动相似,这里仍假设在一段时间内最多发生一次跳跃,跳跃的幅度服从正态分布项表示在正常的价格波动下股价的预期外收益,JS(t)表示股价非正常波动下的收益.

2.3 Copula函数的选择

本文采用Kolmogorov-Smirnov检验进行最优Copula函数的选取.Kolmogorov-Smirnov检验用于检验两样本是否服从相同的分布,此处用于检验拟合出的Copula与经验Copula是否为同一分布,并用检验的P值作为不同拟合模型的判别标准:P值越大,说明拟合效果越好,然后用极大似然法估计Copula的参数.

2.4 CoCo和CoCoCo债券定价模型

Serjantov考虑了CoCo债券同时发生减记和违约的情况,并使用Copula函数刻画二者之间的相关性.然而就CoCo债券的作用来看,它的目的主要是为高等级债权人提供损失的缓冲,保障银行经营的稳健.因此在实际发行中,Basel银行监管委员会及我国银监会都要求在减记条款中加入监管层指定的条款,即当监管机构认定银行陷入危机需要救助时,可以要求CoCo债券进行减记.基于此,假设减记事件始终发生在银行违约之前.因此,一个本金为N,到期日为T的CoCo债券的价格为

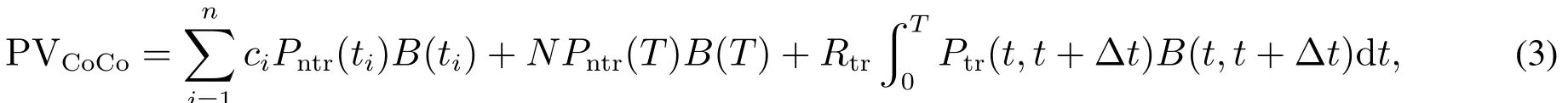
其中ti,i=1,2,...,n为付息时间,ci为息票,B(ti)、B(T)及B(t,t+Δt)为贴现因子,Δt为两次付息之间的时间间隔,Ptr和Pntr分别表示CoCo债券发生和未发生减记的概率,Rtr表示减记时的回收额,在数值上等于减记时得到的股票的价值与减记债票面价值的比值.由上式可以看出,CoCo债券的价值由未减记时普通债券的息票和本金的现值及减记时回收的本金或转换出的股票的现值两部分构成.

特别地,CoCoCo债券的理论价格为

其中Pntr,nc、Ptr,nc及Pntr,c分别表示CoCoCo债券既未减记也未转股的概率、发生减记但未行使转股权的概率及未减记但发生转股的概率,Rtr,nc与Rntr,c分别表示减记但未行使转股权和行使转股权但未减记时的回收额.

由上式可知,CoCoCo债券的价值由三部分构成:CoCoCo债券既未减记也未转股时作为普通债券的息票和本金的现值、减记时回收的本金或转换出的股票的现值、以及根据转换期权条款转换成的股票的现值.由于转股权的行使对应银行经营良好的情况,而减记对应了银行经营陷入危机的情况,因而这里没有考虑二者同时发生的情况.

3 关于塞浦路斯银行CECS的实证定价

塞浦路斯银行于2011–06–02发行,2011–06–10上市交易,并于2012–12–31触发减记条款的CECS(convertible enhanced capital securities)是到目前为止唯一触发减记条款的CoCoCo债券,因此本节选取该产品作为实证研究对象来检验模型的定价效果.实证研究中使用了塞浦路斯银行的股价、银行核心一级资本比率以及减记债的相关历史数据,数据来源于Bloomberg终端.由于CECS的条款较为复杂,本文模型不能详尽地考虑所有条款,因而做了以下简化假设:由于CECS的息票取消条款以银行或中央银行的决定作为判断标准,很难使用定量模型进行刻画,因此模型中未考虑这一条款对价格的影响.单从这一点考虑,模型的理论价格应该高于实际价格.

为了专注于CTR与股票价格之间的Copula相关性,模型假设无风险利率是常数.考虑到CECS使用6个月Euribor(欧元银行同业拆借利率)作为基准利率,因此模型中将使用定价日前一段时间6个月Euribor作为无风险利率.计算减记概率时,在用蒙特卡罗法模拟出的CTR路径的基础上,根据CECS的减记条款“核心一级资本比率CTR小于5%”计算出减记概率.

CECS是无期限的CoCoCo债券,即若CECS没有减记或行权,CECS将一直存续.这里应用模型时只对价格估计日之后的40年时间进行模拟,若在模拟结果中40年后仍未减记或行权,则假设CoCoCo债券按照减记条款转换为普通股.

CECS条款中减记时的转换价格为减记日前5日按成交量加权平均的股票价格,由于交易量数据难以获得,所以在估计时使用减记日前5日收盘价的简单平均作为减记的转换价格.

在考虑转换期权的行使时间时,假设股票支付的股利为0.在每一个行权期间内,转换期权与美式期权十分相似.因为对于标的为不支付股利股票的美式看涨期权,不应提前行使期权,所以假设只在每个行权期间的最后一天行使期权.进一步假设,若在某个行权期间的最后一天转换期权的内在价值大于0,即股价高于行权价格,持有人将行使期权,而不会等到下一个行权期.

3.1 模型参数估计

首先基于历史数据进行参数估计,在不同参数下分别模拟过去一段时间的股价及CTR,并计算与历史数据的欧氏距离,距离最小时的参数即为最优参数.利用此方法得到最优参数估计值如表1和表2.随后应用Kolmogorov-Smirnov检验选择最优Copula,备选的Copula包括高斯Copula,t-Copula,Clayton Copula, Frank Copula和Gumbel Copula,检验结果如表3.根据检验结果发现Clayton Copula是最优选择.最后用极大似然估计法得到Clayton Copula的参数θCl为1.116.

表1 CTR边缘分布的参数估计Table 1 Parameter estimation for CTR’s marginal distribution

表2 股价边缘分布的参数估计Table 2 Parameter estimation for stock return’s marginal distribution

表3 不同Copula的Kolmogorov-Smirnov检验结果Table 3 Kolmogorov-Smirnov testresults

3.2 实证定价结果和敏感度分析

本节对塞浦路斯银行的CECS进行实证定价,然后对参数进行敏感度分析.

3.2.1 实证定价结果

根据CECS的条款,该CECS的面值为100,票面利率为前10次付息按6.5%固定利率,之后按照6个月Euribor+3%作为年化利率,每6个月更新一次.首次付息日为2011–12–31,然后每年6月30日及12月31日付息.减记条款为下列两项之一:1)CTR(实行Basel III之前)或普通股权一级资本比率(实行Basel III之后)低于5%;2)塞浦路斯中央银行认定塞浦路斯银行不能满足资本充足率要求.强制转换价格使用触发减记前5日的平均收盘价,但不高于3.3 EUR,且不低于1.0 EUR.行权价格为3.30 EUR.

在参数估计的基础上,先应用Clayton Copula和式(1),式(2)模拟塞浦路斯银行的将来股价和CTR,进而根据减记条款计算减记概率和行权概率,然后由式(4)计算CECS的价格,计算结果如表4及图1所示.为了比较,同时也给出了假设CTR与股价独立时的定价结果.

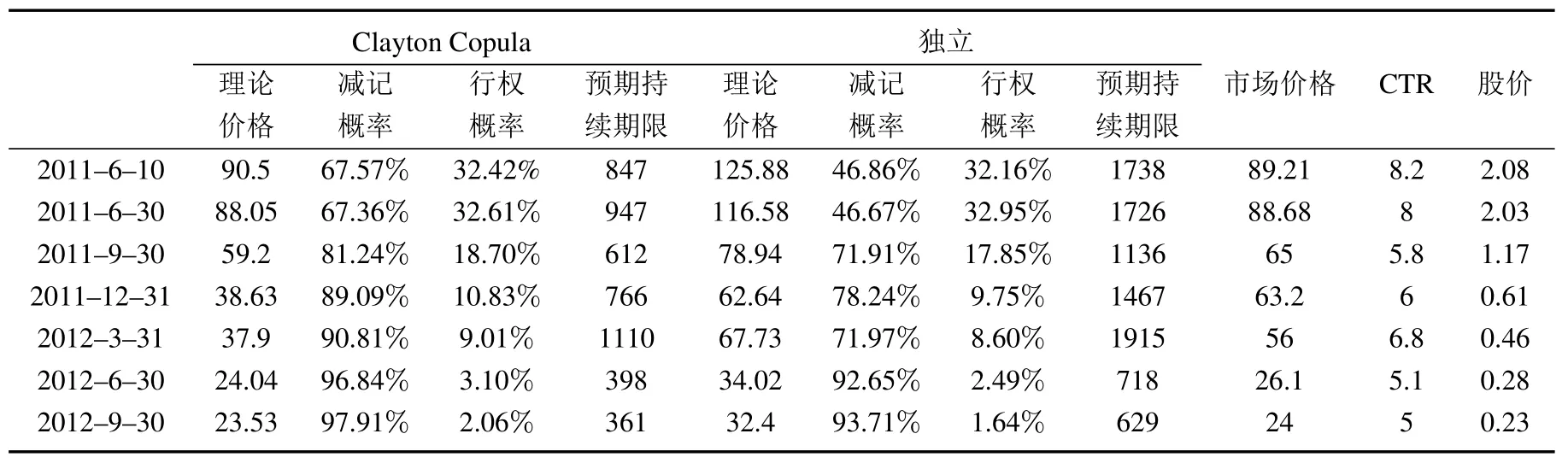
表4 各季度末不同相关性假设下塞浦路斯银行CECS的定价结果Table 4 Pricing results under different correlation assumption

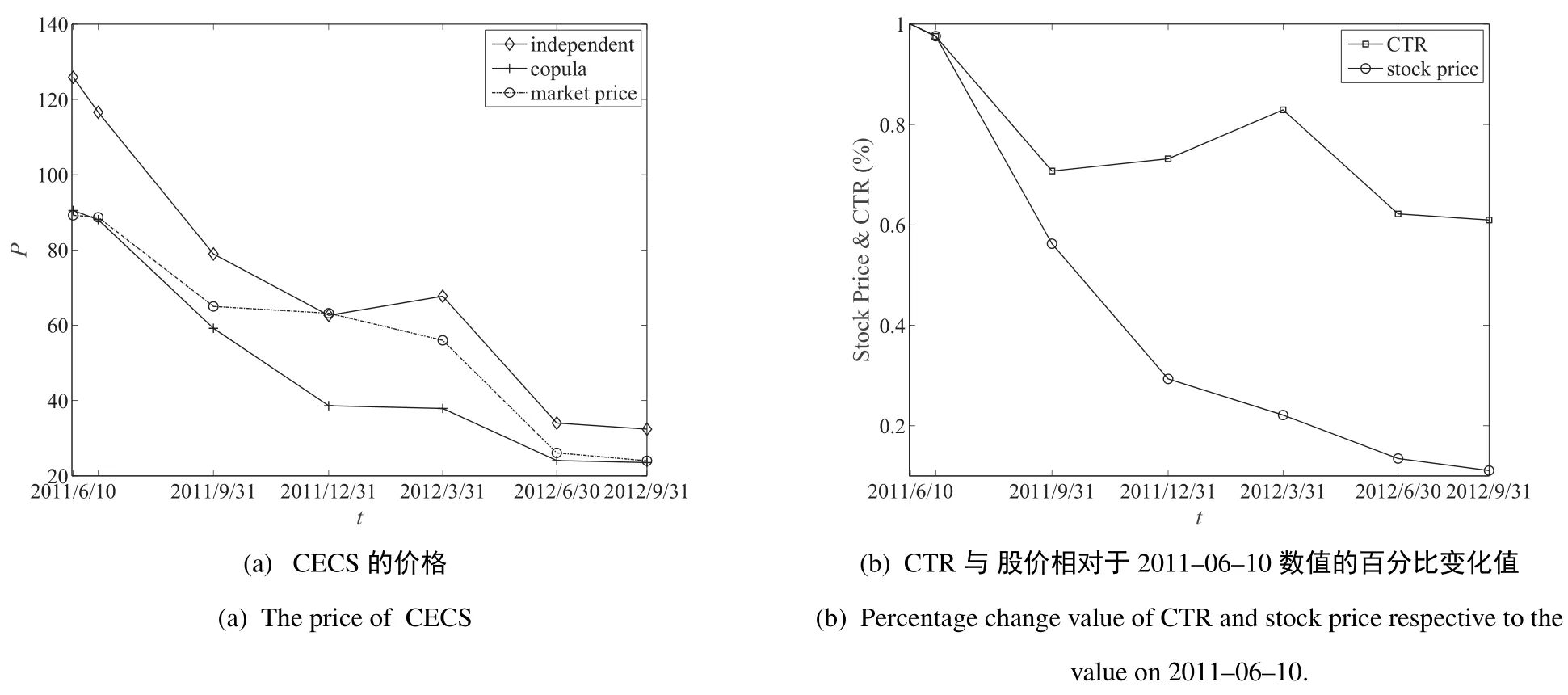
图1 不同相关性假设下塞浦路斯银行的CECS各季度末定价结果对比Fig.1 Pricing results of CECS under different correlation assumptions

由图1可以看出,用Clayton Copula度量CTR和股价相关性时得到的价格要明显低于假设二者独立时的CECS价格,其主要原因在于,相比于假设二者相互独立,使用Clayton Copula度量相关性时更好地估计了两者的尾部风险,因此估计出的减记概率要高出很多,而两种假设下对于行权概率的估计结果差别不大.

为了更好地比较两种相关性假设下的计算结果,在表5中给出了塞浦路斯银行CECS的理论价格与市场价格的百分比偏差,如下表5.由表5可以看出,与市场价格相比,假设独立时的理论价格相对高估:除2011–12–31对价格的估计比较准确外,其余各点与市场价格的偏差均在20%以上.由此可以认为,假设股价与CTR相互独立时估计出的理论价格与市场价格偏差过大,不能反映CECS的实际风险水平.

使用Clayton Copula计算出的理论价值在多数时间与市场价格比较接近,而2011–12–31及2012–03–31两次估计的理论价格和市场价格的偏离较大,在30%以上.造成这一现象的原因在于,在这段时间CTR出现了小幅上涨,而股价跌幅较大,二者的走势出现了背离.CECS的市场价格在这段时间受CTR的变动影响较大,并没有出现大幅下跌.当使用Clayton Copula考虑了CTR与股价之间的相关性时,股价的大幅下跌增大了模型对减记概率的估计,使得模型的理论价格低于市场价格.Copula模型由于使用股价数据获得了市场对塞浦路斯银行未来的悲观预期,早于其他投资者预判了CECS的减记风险,而市场价格过于依赖于财报中发布的CTR数据,低估了减记风险.

表5 两种相关性假设下塞浦路斯银行CECS的理论价格与市场价格的百分比偏差Table 5 Bias between theoretical and market prices under two cases

3.2.2 模型对参数的敏感性分析

本节对定价模型中的参数进行敏感性分析,主要是对最优参数值上下变动50%进行分析.图2与图3为CECS实证定价结果以及减记概率对于θS,ρS,θC和θCl四个参数的敏感性分析结果.可以看出,定价结果以及减记概率对θS和ρS的变动均是敏感的,而对θC和θCl的变动并不敏感,其他未画出图像的参数与θC和θCl结果类似,敏感性不高.

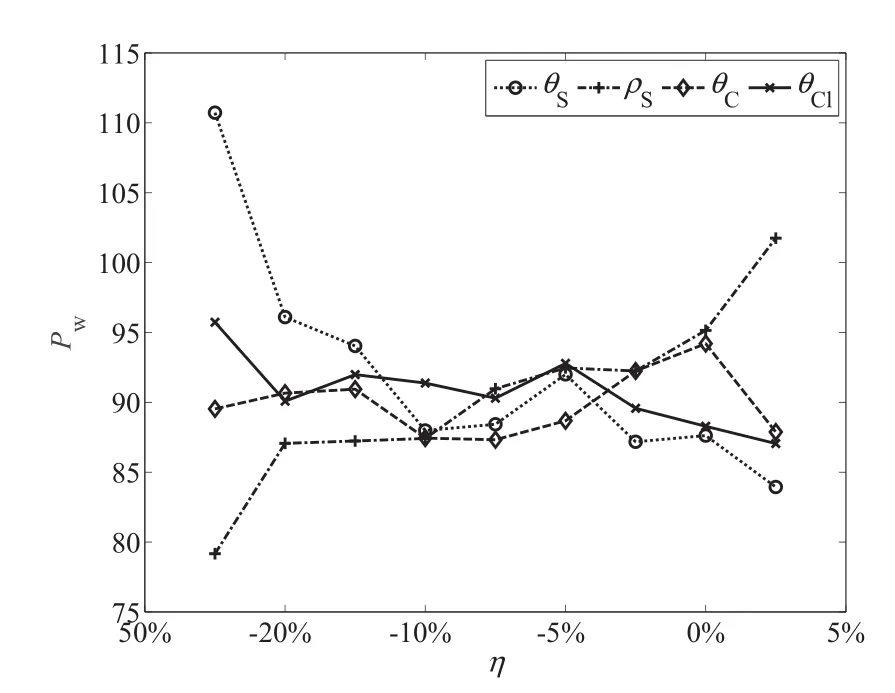
图2 塞浦路斯银行CECS的理论价格对各参数的敏感性分析Fig.2 Sensitivity analysis of CECS’theoretical price to parameters

图3 塞浦路斯银行CECS的减记概率对各参数的敏感性分析Fig.3 Sensitivity analysis of CECS’exercise probability to parameters

θS表示股价波动率的长期回复均值,股价的波动率从长期来看围绕这一均值波动.θS减小(增大)会使得估计出的股价出现大幅波动的概率减小(增大).由于在发行日塞浦路斯银行的CTR距离减记值较远,股价波动率的降低也造成了CTR估计值的波动率降低,使得减记概率大幅下降.因此在θS减小时会使得模型估计的价格变高.

ρS反映的是股价率波动率与股价收益率之间的相关性.由式(2),ρS增大(减小)时,股价收益率波动率与股价收益率产生同向变动的概率增大(减小),这使得股价收益率获得正向大幅波动和较小波动的概率增大(减小),这意味着尖峰厚尾特征更加明显(不明显),并且正向的厚尾要大于负向的厚尾.因此模型估计减记概率随ρS增大而减小,估计价格随ρS增大而增大.

这里的敏感性分析结果与3.2.1节的实证定价分析结果一致,即定价结果受到股价的影响较大,而受到CTR变动的影响较小.这也是股价与CTR出现走势背离时模型定价结果与市场价格出现背离的原因.

4 中国版CoCo与CoCoCo债券的设计与定价

3.2 节选取塞浦路斯银行发行的CECS作为实证研究对象,检验了本文模型的定价效果,并进行了模型的参数的敏感性分析.这一节将借鉴国际上CoCo债券与CoCoCo债券的发行经验,并结合国内市场的实际情况,进行中国版CoCo和CoCoCo债券(减记债)的设计与定价,计算方法与实证定价中使用的方法相同.

虽然平安银行于2014年3月发行了国内首只上市交易的减记债,但该减记债的设计比较简单,没有使用CTR作为减记指标,因此不将其作为研究对象,而是结合国际上已发行的CoCo和CoCoCo债券的条款以及中国银监会对减记债的要求,设计一款新的银行减记债,并对其进行定价.

4.1 中国版CoCo和CoCo Co债券条款设计

表6给出了参考国际上已发行的CoCo和CoCoCo债券的相关条款,以及银监会对于减记债的基本要求设计的一款中国交通银行CoCoCo债券(减记债).该表主要包括三部分:基本条款、减记条款和期权转换条款.如果没有第三部分的期权转换条款,该债券就是CoCo债券.假设该减记债为其他一级资本工具的监管范围,设定减记事件时直接使用了银监会的要求,而没有加入更多的减记条件.

表6 中国交通银行CoCoCo债券条款设计Table 6 Key terms of CBC’s CoCo and CoCoCo bonds

在银行的选择标准上,本文选取市场化程度相对较高且在国内市场有一定影响力的上市银行.交通银行是中国第一家全国性的国有股份制商业银行,已在香港联交所和上海证券交易所两地上市,是国内最大的股份制银行.

在设定转换期权条款时,参考中国工商银行和中国银行发行的可转债相关条款,使用交通银行过去3年历史价格的75%分位数作为行权价格,发行3年后可行使转换期权,并且每年6月及12月最后一个交易日为期权的行权日.由于不发放股利的美式看涨期权不应该提前行权,而我国股市的红利发放并不在6月和12月,因而行权日是6月和12月整月还是最后一个交易日本质上没有区别.在票面利率的设定上,由于在实际发行中一般是招标发行,即票面利率由市场决定,因此将对不同的票面利率进行试算,然后计算出减记债平价发行的票面利率.

4.2 参数估计

下面用交通银行上市以来的股价数据及财务数据对交通银行的CTR和股价的边缘分布进行参数估计,数据来源于万得数据库,估计结果如表7和表8所示.然后用Kolmogorov-Smirnov检验来选择最优Copula,结果如表9.检验结果显示,Clayton Copula的拟合效果最好,与第3节的实证结果一致.θCl的极大似然估计值为0.033 5.

表7 交通银行CTR的边缘分布参数估计结果Table 7 Parameter estimation for the CTR’s marginal distribution

表8 交通银行股价的边缘分布参数估计结果Table 8 Parameter estimation for the stock return’s marginal distribution

表9 不同Copula下的Kolmogorov-Smirnov检验结果Table 9 Kolmogorov-Smirnov test results

4.3 交通银行CoCo和CoCoCo债券定价

这一部分将在不同票面利率下,计算4.1节中设计的交通银行CoCo和CoCoCo债券的价格.假设减记债的面值为100元,票面利率为3%,选用最新一日(2014–03月–13)的国债收益率曲线作为定价中的贴现率,并假设收益率曲线在减记债持续期内不发生变化.

先用4.2节中估计的参数和Clayton Copula,对交通银行的将来股价和CTR进行10万次Monte Carlo模拟,然后根据模型路径和减记事件的设定得到减记概率为30.2%,行权概率为25.3%,预期持续期为2 208 d.进而分别由公式(3)和(4)得到票面利率为3%时所设计的交通银行CoCo和CoCoCo债券的理论价格分别为52.5元和107.3元.

由于票面利率的变动并不影响减记概率、行权概率以及预期持续期,因而在计算不同票面利率下的减记债价格时没有再进行更多的Monte Carlo模拟,而是在3%票面利率下的理论价格的基础上,用息票的预期折现价值对理论价格进行调整.在持续期为2 208 d时,1%息票的折现值为5.51元.这样可以得到CoCo和CoCoCo债券平价发行时的票面利率分别为10.30%和1.68%.

表10给出了对于是否考虑转换期权的交通银行减记债(分别对应于CoCo债券和CoCoCo债券)的计算结果,即CoCoCo债券包含表6中的全部条款,CoCo债券包含基本条款和减记条款两部分.

表10 交通银行CoCo和CoCoCo债券的计算结果比较Table 10 Pricing results for CBC’s CoCo and CoCoCo bonds

因为CoCoCo债券比普通的可转债多了不利于债券持有者的减记条款,而比CoCo债券多了有利于债券持有者的期权转换条款,所以从理论上讲,CoCoCo债券的票面利率应该高于同一银行发行的可转债的票面利率,而低于同一银行发行的CoCo债券的票面利率,而CoCo债券的票面利率应高于同一银行发行的普通债券.由表10可以看出,模型估计的CoCoCo债券票面利率(1.68%)高于当前市场上上市银行可转债的平均票面利率(1.03%),而低于模型估计的CoCo债券票面利率(10.3%);与此同时,模型估计的CoCo债券票面利率(10.3%)高于交通银行普通债券的平均利率(5.62%),与理论预期相符.从以上对比可知,CoCoCo债券的利率要远低于普通债券及CoCo债券.

可以认为,CoCoCo型减记债在为银行补充资本金的同时,还可以以较低成本进行融资,而CoCo债券的发行将给银行带来较大的利息支出压力.从这点来看,发行CoCoCo债券将是比CoCo债券更好的选择.这里对于资金成本的讨论仅为初步讨论,并没有将转换期权成本以及不同到期期限对利率的影响考虑进来.

5 结束语

本文应用Clayton Copula对股价与CTR两个变量间的相关性进行了刻画,建立了CoCo和CoCoCo债券的定价模型,然后分别对塞浦路斯银行的CECS以及所设计的中国交通银行减记债进行了定价和敏感度分析.

以往的研究认为,由于CTR数据频率低并且易人为操纵,CTR对未来风险的估计精确度比股价数据要差很多.使用Copula函数将两变量联系起来为CTR数据的使用带来以下优点:一方面可以用较精确的股价数据对CTR的估计进行修正,另一方面,当CTR没有新数据到达时,可以利用股价的变动将市场观点考虑到对减记概率的估计中来.

实证结果显示,使用Copula刻画股价与CTR之间的相关性得到的定价结果明显好于假设二者独立时的结果,并且当CTR与股价走势出现背离时,使用Copula刻画相关性可以提前预判银行的风险,而市场价格则过于看重减记指标CTR的变动,低估了当时的减记风险.

在数值分析中,使用交通银行的数据进行了虚拟发行定价.结果显示,CoCoCo债券由于有获得嵌入的期权收益的可能性,使得其票面利率要低于普通债券.这样使银行在获得资本金的同时减少了利息支出的压力,而CoCo债券的票面利率则超过10%,对银行造成了较大的利息支出压力.因此,从银行角度来看CoCoCo型减记债是更好地选择.

[1]赵英杰.减记债：国外经验与中国实践.证券法苑,2014(11):105–141. Zhao Y J.Write-down bond:Foreign experience and China’s practice.Securities Law Review,2014(11):105–141.(in Chinese)

[2]Madan D B,Schoutens W.Conic coconuts:The pricing of contingent capital notes using conic fnance.Mathematics&Financial Economics,2010,4(2):87–106.

[3]Barucci E,Viva L D.Dynamic capital structure and the contingent capital option.Annals of Finance,2010,9(3):337–364.

[4]Pelger M.Contingent Convertible Bonds:Pricing,Dilution Costs and Effcient Regulation.Social Science Electronic Publishing, 2012.

[5]Chen N,Glasserman P,Nouri B,et al.CoCos,Bail-in,and Tail Risk.Washington DC:Offce of Financial Research,2013.

[6]Pennacchi G,Vermaelen T,Wolff C C P.Contingent capital:The case of COERCs.Journal of Financial and Quantitative Analysis, 2014,49(3):541–574.

[7]Yang Z J,Zhao Z I.Valuation and analysis of contingent convertible securities with jump risk.International Review of Financial Analysis,2015,41:124–135.

[8]Spiegeleer J D,Schoutens W.Pricing contingent convertibles:A derivatives approach.Social Science Research Network Electronic Journal,2011,20(2):27–36.

[9]Brandt M,Hermansson C.Pricing Contingent Convertibles in an Intensity based Model.Gothenburg:Gothenburg Uuniversity,2013.

[10]Cheridito P,Xu Z.A reduced-form contingent convertible bond model with deterministic conversion intensity.Journal of Risk,2014, 17(3):1–18.

[11]Corcuera J M,Spiegeleer J D,Fajardo J,et al.Close form pricing formulas for coupon cancellable cocos.Journal of Banking& Finance,2014,42:339–351.

[12]Hillion P,Vermaelen T.Death spiral convertibles.Journal of Financial Economics,2004,71(2):381–415.

[13]Veiteberg V G,Bysveen F T,Rosef B H.Pricing Contingent Convertible Capital:An Empirical Approach.Trondheim,Norway: Norway University of Science and Technology,2012.

[14]王晓林,杨招军.基于效用的公司证券定价与资本结构选择.系统工程理论与实践,2014,34(1):13–24. Wang X L,Yang Z J.Utility-based pricing of corporate securities and capital structure choice.Systems Engineering:Theory and Practice,2014,34(1):13–24.(in Chinese)

[15]秦学志,胡友群,李静一.或有可转债对银行资本结构及其价值的影响:基于触发点差异的研究.系统管理学报,2014,23(2): 191–199. Qin X Z,Hu Y Q,Li J Y.Impact of contingent convertible bonds on the bank’s capital structure and value:An investigation based on difference of trigger points.Journal of Systems and Management,2014,23(2):191–199.(in Chinese)

[16]秦学志,胡友群,尚 勤,等.基于转换点生存概率的或有可转债定价研究.管理工程学报,2015,29(2):182–189. Qin X Z,Hu Y Q,Shang Q,et al.Reaearch on pricing contingent convertible bonds with survival probability-based trigger.Journal of Industrial Engineering Management,2015,29(2):182–189.(in Chinese)

[17]Girolamo F D,Campolongo F,De Spiegeleer J,et al.Contingent Conversion Convertible Bond:New Avenue to Raise Bank Capital. Ispra,Italy:Joint Research Centre,2012

[18]Li D X,On default correlation：A Copula approach.Journal of Fixed Income,2000,9(4):43–54.

[19]Hull J,White A.Valuation of a CDO andnthto default CDS without monte carlo simulation.Journal of Derivatives,2004,12(2): 8–23.

[20]艾春荣,张 奕,崔长峰.债券流动性与违约风险相关性溢价及实证研究.管理科学学报,2015,18(5):87–94. Ai C R,Zhang Y,Cui C F.Bond’s liquidity and default risk correlation premium and empirical test.Journal of Management Sciences in China,2015,18(5):87–94.(in Chinese)

[21]周孝华,张保帅,董耀武.基于Copula-SV-GPD模型的投资组合风险度量.管理科学学报,2012,15(12):70–78. Zhou X H,Zhang B S,Dong Y W.Risk measurement of fnancial portfolio based on Copula-SV-GPD model.Journal of Management Sciences in China,2012,15(12):70–78.(in Chinese)

[22]Li P,Li Z.Change analysis of dependence structure and dynamic pricing of basket default swaps.European Financial Management, 2015,21(4):646–671.

[23]Serjantov A.On Practical Pricing Hybrid Capital Securities.Barcelona,Spain:Global Derivatives and Risk Management Research Center,2011.

[24]Vasicek O.An equilibrium characterization of the term structure.Journal of Financial Economics,1977,5(2):177–188.

[25]Ball C A,Torous W N.A simplifed jump process for common stock returns.Journal of Financial&Quantitative Analysis,1983, 18(1):53–65.

[26]Heston S L.A closed-form solution for options with stochastic volatility with applications to bond and currency options.Review of Financial Studies,1993,6(2):327–343.

CoCo bonds pricing based on Copulas bivariate simulation

Li Ping1,Yin Jinghua2,Lai Na1,Huang Guangdong3*
(1.School of Economics and Management,Beihang University,Beijing 100191,China; 2.Guangfa Securities,Guangzhou 510075,China 3.School of Science,China University of Geosciences(Beijing),Beijing 100191,China)

The correlation of stock price and core tier 1 ratio(CTR)is described by using a copula function. By simulating the stock price and CTR,the pricing models of CoCo bonds and CoCoCo bonds are established. The empirical study on the CECS(convertible enhanced capital securities)issued by Bank of Cyprus shows that the pricing results under the copula dependence structure are better than those assuming independent. Finally,combining with the relevant provisions of existing international CoCo and CoCoCo bonds and the basic requirements of China Banking Regulatory Commission for write-down debts,the Chinese version of CoCo and CoCoCo bonds for the Bank of Communications are designed as exsamples,and the numerical calculation based on the given pricing model is implemented.

CoCo bond;CoCoCo bond;core tier 1 capital ratio;Clayton Copula

TP273

A

1000-5781(2016)06-0772-11

10.13383/j.cnki.jse.2016.06.006

李 平(1972—),女,湖北南漳人,博士,教授,金融工程,Email:liping124@buaa.edu.cn;

尹菁华(1987—),男,辽宁抚顺人,硕士,投资经理助理,金融工程,Email:yinjinghua@gf.com.cn;

来 娜(1984—),女,山西临汾人,硕士生,金融工程,Email:18810833006@163.com;

黄光东(1971—),男,湖北宜城人,博士,副教授,应用数学,Email:gdhuang@cugb.edu.cn.

2016-01-07;

2016-07-25.

国家自然科学基金资助项目(71271015;71571008);中央高校基础科研业务费专项资金资助项目(2652013106).

*通信作者