Stopping Means Achieving: A Weaker Logic of Knowing How*

Yanjun Li

Faculty of Philosophy,University of Groningeny.j.li@rug.nl

Stopping Means Achieving: A Weaker Logic of Knowing How*

Yanjun Li

Faculty of Philosophy,University of Groningeny.j.li@rug.nl

.This paper proposes a weaker but more realistic semantics to the knowing-how operator proposed by Y.Wang in 2015.According to this semantics,an agent knows how to achieveφgivenψif(s)he has a finite linearplan by which(s)he can always end up with aφ-state when the execution of the plan terminates,either successfully or not.This weaker interpretation of knowing-how results in a weaker logic where the composition axiom in Wang’s paper no longer holds.We present a sound and complete axiomatic system of this logic and prove that this logic is decidable.

1 Introduction

Epistemic logic proposed by von Wright and Hintikka[14,26]is a modal logic that is concerned with reasoning about knowledge.It formalizes the propositional knowledge,knowledge of the form“knowing that”,as a modal formulaKφwhich expressesthe agentknowsthatφholds.Itinterpretsknowledge-thatregarding agents’uncertainty.The agent knows thatφata statesifand only ifhe can rule out allthe¬φepistemic possibilities ats.Epistemic logic is widely applied in theoretical computer science,artificial intelligence,economic and linguistics(see[4]).

However,knowledge is not only expressed by“knowing that”,but also by other expressions,such as“knowing how”,“knowing what”,“knowing why”,and so on. Among all these expressions,“knowing how”(and the knowledge-how that it expresses)is the most discussed one.Despite the heated philosophical discussions on whether knowledge-how is a subspecies of knowledge-that(see the survey by [7]),researchers in artificial intelligence and logic have largely adopted the view that knowledge-how can be reduced to knowledge-that and ability.

In artificial intelligence,beginning from McCarthy and Hayes([16,17]),researchers started to study what it means for a computer program to“know how”toachieve a state of affairsφin terms of its ability.In particular,Moore’s work([18]) is highly influential on representation and reasoning of knowledge and ability.According to Moore,there are two possible ways to define the agent’s knowledge-how:

(I)There exists an actionasuch that the agent knows that the performance ofawill result inφ;

(II)The agent knows that there exists an actionasuch that the performance ofawill result inφ.

The first is ade redefinition of knowledge-how,and the second is ade dictodefinition.Moore pointed out that the first definition is too strong and the second is too weak.Therefore,he proposed an adapted,but very complicated version of the definition.Moore’s formalism has inspired a large body of work in artificial intelligence on knowledge and ability([9,1]).

In logic,the framework of Alternating-time Temporal Logic(ATL)is concerned with reasoning about agent’s abilities in game structures.By adding the knowledge operator to this framework(see[2]),it can express that the agent knows that there is a strategy to enforceφfrom the current state.However,it is still ade dictoreading of knowledge-how,and it is too weak to define knowledge-how.To solve this problem, researchersproposed differentsolutions([3,12,13]),such asmaking the strategy uniform,or specifying the explicit actions in the modality(e.g.,knowing that performingabcwill achieveφ).

In the above-mentioned works,knowledge-how is usually expressed in a very rich logical language involving quantifiers or various complicated modalities.However,starting from[11,15,19],logiciansattempted to formalize some knowledge-wh, such as“knowing whether”,“knowing what”et al,as a whole modality,in the similar way of epistemic logic dealing with knowledge-that.The recent works([5,6,10,21, 22,23,24])are in line with this idea.

In particular,[21]proposed a single-agentlogic of knowing how,which includes modal formulaKh(ψ,φ)to express that the agent knows how to achieveφgiven the preconditionψ.The models are labelled transition systems which reflect agent’s ability.Thusthe modelsare also calledabilitymaps.The formulaKh(ψ,χ)isinterpreted in ade rereading of knowledge-how:there exists an action sequence(also called a plan)σsuch that(1)performingσat eachψ-state will achieve aφ-state;and(2)the execution of the plan will never fail.In automated planning,such a plan is called aconformant plan(cf.[8,20]).Considering Example 1 which represents a map of a floor in a building where the agent can go right(r)or up(u).1This example is taken from[25,27,21].According to Wang’s interpretation of knowledge-how,the agent here knows how to achieveqgivenpbecause there is a conformant planru(first moving right then moving up)for achievingq-states fromp-states.

Example 1

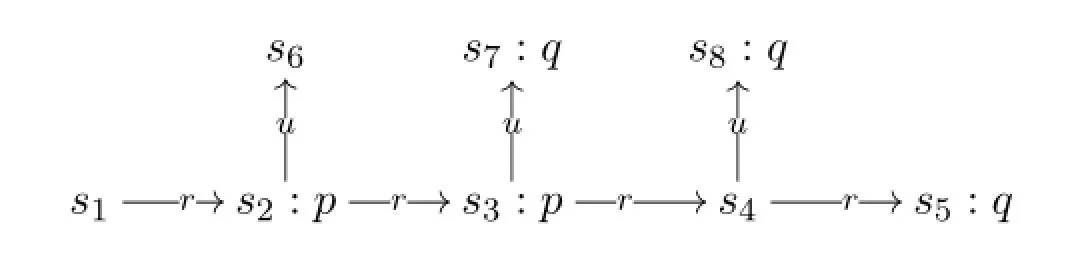
However,the demands that a conformant plan askes may be too strong,in the sense that the execution of the plan willneverfail.Intuitively,we still be comfortable to say“we know how to achieveφgivenψ”only if we will always end up with aφ-state when the execution of the plan terminates,either successfully or not.For example,letqbe true only on the states5in Example 1 then there will be no conformant plans for achieving the onlyq-states5fromp-states,but we still say that“we know how to achieve theq-state fromp-states”because we can get there by moving right at most three times.The plan of moving right three times is not a conformant plan since the execution of the plan starting froms3will fail to continue ats5,but this plan will still guarantee our achieving theq-states5in the sense that we will always end up withs5when the execution of the plan terminates.We call it a weak conformant plan. A weak conformant plan for achievingφ-states fromψ-states is a finite linear action sequence such that the execution of the action sequence at eachψ-state will always terminate on aφ-state,either successfully or not.Intuitively,a weak conformant plan is enough for our knowing how to achieveφgivenψ.

This paper interprets the knowledge-how formulaKh(ψ,φ)as that there is a weak conformant plan for achievingφgivenψ.Compared to the interpretation of [21],our interpretation is weaker,but it is more realistic.We also present a sound and complete axiomatic system.It shows that this weaker interpretation results in a weaker logic.The composition axiom in[21]

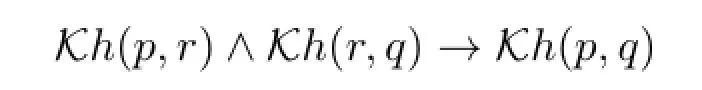
is not valid under this weaker semantic.Even though the logic is weaker,the proof of the completenessisnon-trivial.We also define an alternative non-standard semantics. By reducing a decidable problem w.r.t.our weaker semantics to a decidable problem w.r.t.this alternative non-standard semantics,we show that this logic is decidable. Whatismore,from the perspective ofthe non-standard semantics,we can see thatour interpretation of knowledge-how is almost the same with Moore’s first interpretation (I).

The rest of the paper is organized as follows.Section 2 introduces the language and semantics.Section 3 presents an axiomatic system,which is weaker than the system given in[21].Section 4 shows that our logic is decidable by reducing a standard decidable problem to a decidable problem w.r.t.the non-standard semantics.In the last section,we conclude with future directions.

2 Language and semantics

In this section,we will introduce the language and the semantics.The language is the same as[21].The intuition of the semantics is that we know how to achieveφgivenψif and only if we have a weak conformant plan for achievingφ-states fromψ-states.

Definition 1(Language)Given a set of proposition lettersP,the languageLis defined as follows:

wherep∈P.KhW(ψ,φ)expresses that the agent knows how to achieveφgivenψ. We use the standard abbreviations⊥,φ∨ψandφ→ψ.The same as[21],we defineUφasKhW(¬φ,⊥).Uis intended to be a universal modality,and it will become more clear after we define the semantics.

Definition 2(Model)A model(also called an ability map)is essentially a labelled transition system(S,Σ,R,V)where:

·Sis a non-empty set of states;

·Σ is a set of actions(or labels);

·R:Σ→2S×Sis a collection of transitions labelled by actions in Σ;

·V:S→2Pis a valuation function.

Definition 3(Terminal States)Given a states∈Sand an action sequenceσ=a1···an∈Σ∗,TERMS(s,σ)is the set of states at which executingσonsmight terminate.Formally,it is defined as

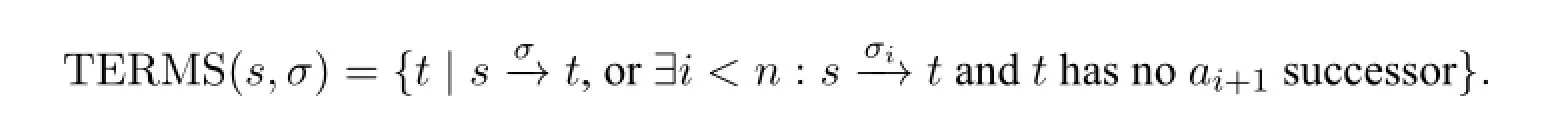
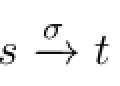
Definition 4(Semantics)Supposesis a state in a modelM=(S,Σ,R,V).Then

we inductively define the notion of a formulaφbeing satisfied(or true)inMat statesas follows:

where〚ψ〛={s∈S|M,s⊨ψ}.

We also call the semantics defined here as the standard semantics,to distinguish it from the non-standard semantics defined in Section 4.Now we can also check that the operatorUdefined byKhW(¬φ,⊥)is indeed auniversal modality:

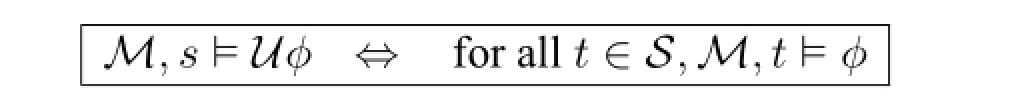
Under this semantics,the composition axiom in[21],

isnotvalid.The following example presentsa modelon which the composition axiom is not true.

Example 2ModelMis depicted as follows.

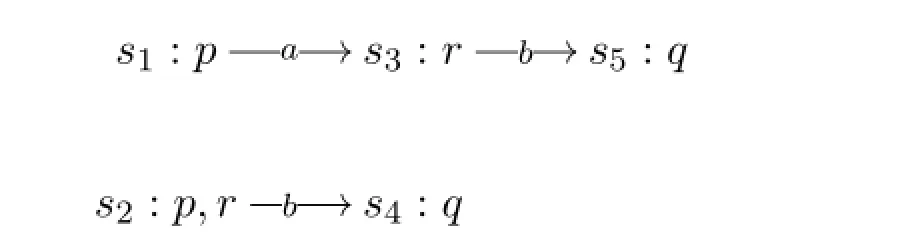
·M,s1⊨KhW(p,r)since there is a weak conformant plana.Please note that executingaons2will terminate on itself.

·M,s1⊨KhW(r,q)since there is a weak conformant planb.Executingbon eachr-states,eithers3ors2,will achieving on aq-state.

·M,s1⊭KhW(p,q)since there are no weak conformant plans for achievingq-states fromp-states.Particularly,abis not a weak conformant plan.The performance ofabons1will result in aq-states5,but executingabonp-states2will terminate on itself.

The composition of two weak conformant plan might not be a weak conformant plan any more.Just as it is shown in Example 2,ais a weak conformant plan for achievingr-states fromp-states,andbis a weak conformant plan for achievingqstates fromr-states,but the compositionabis not a weak conformant plan for achievingq-states fromp-states.There are no weak conformant plans for how to achieveq-states fromp-states in this example.

Definition 5(SKℍ System)The axiomatic system SKℍ is defined in Table 1.We write SKℍ⊢φ(or sometimes just⊢φ)to mean that the formulaφis derivable in the axiomatic system SKℍ;the negation of SKℍ⊢φis written SKℍ⊬φ(or just⊬φ).To say thata setDofformulasis SKℍ-inconsistent(orjustinconsistent)means that there is a finite subsetD′⊆Dsuch that⊢¬∧D′,where∧D′:=∧φ∈D′φ

ifD′/=Øand∧φ∈Øφ:=⊤.To say that a set of formulas is SKℍ-consistent(or just consistent)means that the set of formulas is not inconsistent.Consistency or inconsistency of a formula refers to the consistency or inconsistency of the singleton set containing the formula.

Table 1:System SKℍM

All the axioms here except UKh are also axioms in the axiomatic system addressed in[21],where UKh is deducible from the composition axiom.As observed in Example 2,The composition axiom is not valid by our semantics.It means that the system here is strictly weaker than the syetem in[21],which is in line with the fact that here knowledge-how is interpreted in a weaker way.However,even though the system is weaker,the proof of its completeness is highly non-trivial.We will explain the reason later in the proof.

Proposition 1⊢Uχ∧Uψ→U(χ∧ψ)

Proof(1)⊢χ→(ψ→(χ∧ψ))by propositional logic

(2)⊢U(χ→(ψ→(χ∧ψ)))by Rule NECU

(3)⊢Uχ→U(ψ→(χ∧ψ))by Axiom DISTU

(4)⊢U(ψ→(χ∧ψ))→(Uψ→U(χ∧ψ))by Axiom DISTU

(5)⊢Uχ→(Uψ→U(χ∧ψ))by(3)and(4)

(6)⊢Uχ∧Uψ→U(χ∧ψ)by propositional logic□

Proposition 2⊨U(p′→p)∧U(q→q′)∧KhW(p,q)→KhW(p′,q′)

ProofAssuming thatM,s⊨U(p′→p)∧U(q→q′)∧KhW(p,q),we need to show thatM,s⊨KhW(p′,q′).SinceM,s⊨KhW(p,q),it follows that there existsσ∈Σ∗such that for eachw∈〚p〛and eacht∈TERMS(w,σ)we haveM,t⊨q(∗).In order to showM,s⊨KhW(p′,q′),we only need to show thatM,t′⊨q′for eachw′∈〚p′〛and eacht′∈TERMS(w′,σ).

Givenw′∈〚p′〛,it follows byM,s⊨U(p′→p)thatw′∈〚p〛.Due to(∗),we have that for eacht′∈TERMS(w′,σ):M,t′⊨q,namelyt′∈〚q〛.Moreover,sinceM,s⊨U(q→q′),we have〚q〛⊆〚q′〛.Therefore,we have thatt′∈〚q′〛,namelyM,t′⊨q′,for eacht′∈TERMS(w′,σ).Thus,M,s⊨KhW(p′,q′).□

SinceUis a universal modality,DISTU,TU and EMPKh are obviously valid. Because the modalityKhWis not local,it is easy to show that 4KhU and 5KhU are valid.Along with Propositions 2,we have that all axioms are valid.Moreover,due to a standard argument in modal logic,we know that the rules MP,NECU and SUB preserve formula’s validity.Therefore,the soundness of SKℍ follows immediately.Theorem 1(Soundness)SKℍ is sound w.r.t.the standard semantics.

3 Completeness

This section will show that SKℍ is complete w.r.t.the standard semantics.Here are some notions before we prove the completeness.Given a set ofLformulas Δ,let Δ|KhWand Δ|¬KhWbe the collections of its positive and negativeKhWformulas:

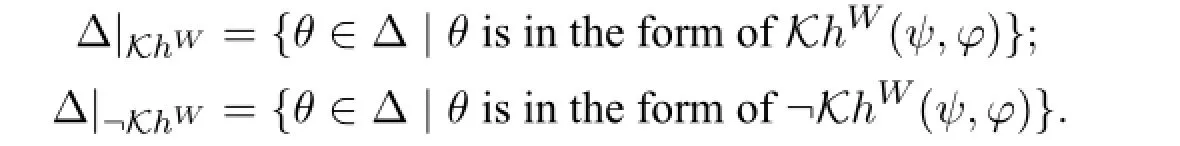
In the following,let Γ be a maximal consistent set(MCS)ofLformulas.We first prepare ourselves with some useful definitions and handy propositions.

Definition 6Let ΦΓbe the set of all MCS Δ such that Δ|KhW=Γ|KhW.

Proposition3ForeachΔ∈ΦΓ,we haveKhW(ψ,φ)∈Γifand only ifKhW(ψ,φ)∈Δ for allKhW(ψ,φ)∈L.

Proposition 4Ifφ∈Δ for all Δ∈ΦΓthenUφ∈Δ for all Δ∈ΦΓ.

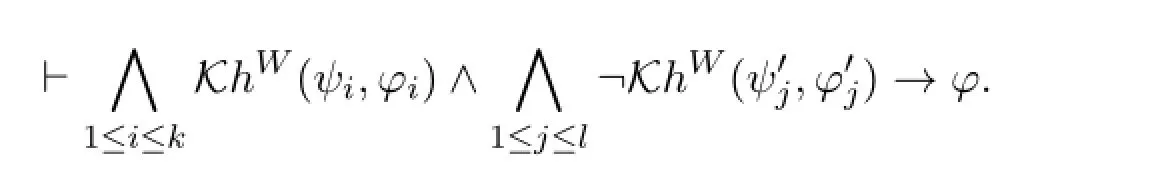
By NECU,

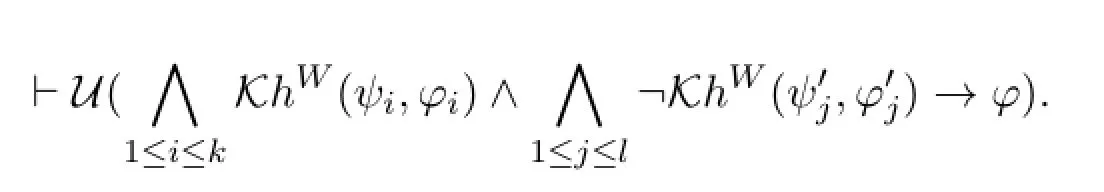
By DISTU we have:

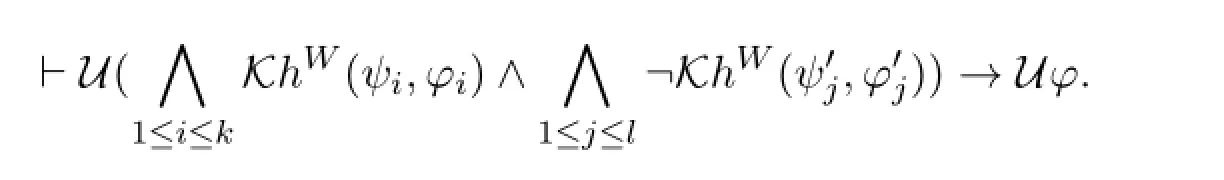
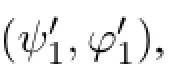
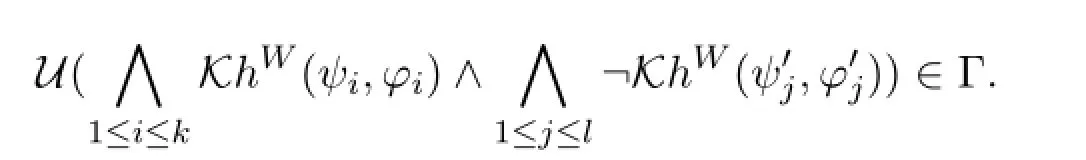
Now it is immediate thatUφ∈Γ.Due to Proposition 3,Uφ∈Δ for all Δ∈ΦΓ.□

Proposition 5GivenKhW(ψ,φ)∈Γ and Δ∈ΦΓ,ifψ∈Δ then there exists Δ′∈ΦΓsuch thatφ∈Δ′.

ProofAssumingKhW(ψ,φ)∈Γandψ∈Δ∈ΦΓ,ifthere doesnotexistΔ′∈ΦΓ

such thatφ∈Δ′,it means that¬φ∈Δ′for all Δ′∈ΦΓ.It follows by Proposition 4 thatU¬φ∈Γ,and thenU(φ→⊥)∈Γ.SinceU(φ→⊥)andKhW(ψ,φ)∈Γ,it follows by UKh thatKhW(ψ,⊥)∈Γ,namelyU¬ψ∈Γ.By Proposition 3,we have thatU¬ψ∈Δ.It follows by TU that¬ψ∈Δ.This is contradictory withψ∈Δ. Therefore,there exists Δ′∈ΦΓsuch thatφ∈Δ′.□

SinceKhWformulas are globally true or false,it is not possible to satisfy each consistentKhWformulas simultaneously in one model.Therefore,in the following, we build a separate canonical model for each MCS Γ.Because the following proofsare quite technical,itiscrucialfirstto understand the ideasbehind the canonicalmodel construction.Besides satisfyingKhW(ψ,φ),the canonical model also needs to meet the following two requirements.

(1)Generally,KhW(ψ,φ)cannot be satisfied by a one-step plan.Otherwise, the canonical model will always satisfy the formula thatKhW(p,¬p)∧KhW(¬p,q)→KhW(p,q)which is not a valid formula.Therefore,in the canonical model,KhW(ψ,φ)willbe satisfied by a two-step plan〈ψ,ψφ〉〈ψφ,φ〉.Ifwe already reach aφ-state by the first step〈ψ,ψφ〉,we do not need to go further anymore.If we arrive at a¬φ-state by〈ψ,ψφ〉,then we need to make sure that doing the second step〈ψφ,φ〉on this state will achieve onlyφ-states.

(2)If〈ψ,ψφ〉〈ψφ,φ〉is a weak conformant plan forKhm(ψ,φ),then〈ψ,ψφ〉must be executable on at least one¬ψ-state.The reason is that if〈ψ,ψφ〉is only executable atψ-states then the canonical model will always satisfyKhW(ψ,φ)→KhW(ψ∨φ,φ)which is not a valid formula.If we allow〈ψ,ψφ〉also executable at¬ψ-states,we must treat the step fromψ-states and¬ψ-states differently.Otherwise, the canonical model will always satisfyKhW(ψ,φ)→KhW(⊤,φ).Our method is that the step〈ψ,ψφ〉starting fromψ-states will reach only states marked withψφ. This is why we includeψφmarkers in the building blocks of the canonical model besides maximal consistent set.2In[21],the canonical models are much simpler:we just need MCSs and the canonical relations are simply labelled by〈ψ,φ〉forKh(ψ,φ)∈Γ.

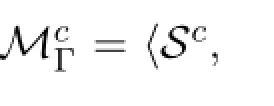
·Sc={(Δ,ψφ)|Δ∈ΦΓ,KhW(ψ,φ)∈Γ}.We write the pair inSasw,v,···,and refer to the first entry ofw∈Sas L(w),to the second entry as R(w);

·ΣΓ={〈ψ,ψφ〉,〈ψφ,φ〉|KhW(ψ,φ)∈Γ};

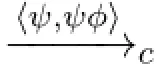
·p∈Vc(w)⇐⇒p∈L(w).

For eachw∈S,we also callwaψ-state ifψ∈L(w).

Please note thatScisnon-empty because(Γ,⊤⊤)∈Sc.We firstshow thateach Δ∈ΦΓappears as L(w)for somew∈Sc.

Proposition 6For each Δ∈ΦΓ,there existsw∈Scsuch that L(w)=Δ.

ProofSince⊢⊤→⊤,it follows by NECU that⊢U(⊤→⊤).Thus,we haveU(⊤→⊤)∈Γ.It follows by EMPKhm thatKhW(⊤,⊤)∈Γ.Thus,we have that(Δ,⊤⊤)∈Sc.□

Since Γ∈ΦΓ,it follows by Proposition 6 thatSc/=Ø.

Proposition 4 helps us to prove the following proposition which will play crucial roles in the completeness proof.Note that according to Proposition 4,to obtain thatUφin alltheΔ∈ΦΓ,we justneed to show thatφisin alltheΔ∈ΦΓ,notnecessarily in all thew∈Sc.

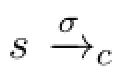
·a1=〈ψ1φ1,φ1〉We willshow thatσ′=ϵsatisfiesthatforeachψ-statew∈Scand each statet∈TERMS(w,σ′)we haveφ∈L(t).We only need to show thatψ→φ∈Δ for each Δ∈ΦΓ.If not,there exists Δ′∈ΦΓsuch that{ψ,¬φ}⊂Δ′.Letχbe a formula such that⊢χ↔ψ1andχ/=ψ1.Since⊢χ→⊤,it follows by NECU and EMPKh thatKhW(χ,⊤)∈Γ.Then we have aψ-statew′=(Δ′,χ⊤)∈Sc.Sinceχ/=ψ1,a1is not executable onw′,and then we have{w′}=TERMS(w′,σ).Since¬φ∈L(w′),this is contradictory with our assumption.Thus we haveψ→φ∈Δ for each Δ∈ΦΓ.

·a1=〈ψ1,ψ1φ1〉There are two cases based on the form ofa2:–a2=〈ψ2,ψ2φ2〉There are two cases:U¬ψ2∈Γ or not.

–a2=〈ψ2φ2,φ2〉There are two cases:U(ψ→ψ1)∈Γ or not.

*There exists Δ∈ΦΓsuch thatψ,¬ψ1∈Δ.In this case,it must be thatφ∈Δ′for each Δ′∈ΦΓ.If not,lett= where¬φ∈Δ′,⊢ψ2↔ψ′2andψ2/=ψ2.Letwbe a state such that

ProofBoolean cases are trivial,and we only focus on the case ofKhW(ψ,φ).

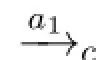
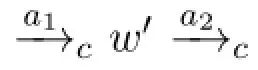
·n=0 It meansσ=ϵ.It follows by HI thatψ∈Δ impliesφ∈Δ for all Δ∈ΦΓ.Therefore,we haveψ→φ∈Δ for all Δ∈ΦΓ.It follows by Proposition 4 thatU(ψ→φ)∈Γ.By EMPKh,we havew thatKhW(ψ,φ)∈Γ.It follows by Proposition 3 thatKhW(ψ,φ)∈L(w).

·n＞0 There are three cases.

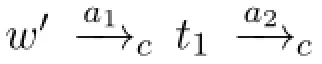
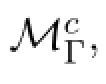
Theorem 2(Completeness)SKℍ is complete w.r.t.the standard semantics.

Similar with the proof of the completeness in[21],our canonical model is also based on a certain maximal consistent set Γ,but there are some critical differences. First,the state of the canonical model is a pair consisting of a maximal consistent set and a marker.The marker plays an important role in defining the binary relations of actions.Second,each knowing-how formula is generally realized by a weak conformant plan consisting of two actions.

4 Decidability

Thissection willshow thatthe problem thatwhethera formulaφisvalid w.r.t.the standard semantics is decidable.The strategy is that we firstly define a non-standard semantics and show thatφis valid w.r.t.the standard semantics if and only ifφis valid w.r.t.the non-standard semantics.Next,we show thatφhas a bounded model ifφis satisfiable w.r.t.the non-standard model.

Definition 8(Non-standard semantics)Given a pointed modelM,sand a formulaφ,we writeM,s⊩φto mean thatφis true atM,sw.r.t.the non-standard semantics⊩.The non-standard semantics⊩is defined by the following induction on formula construction.

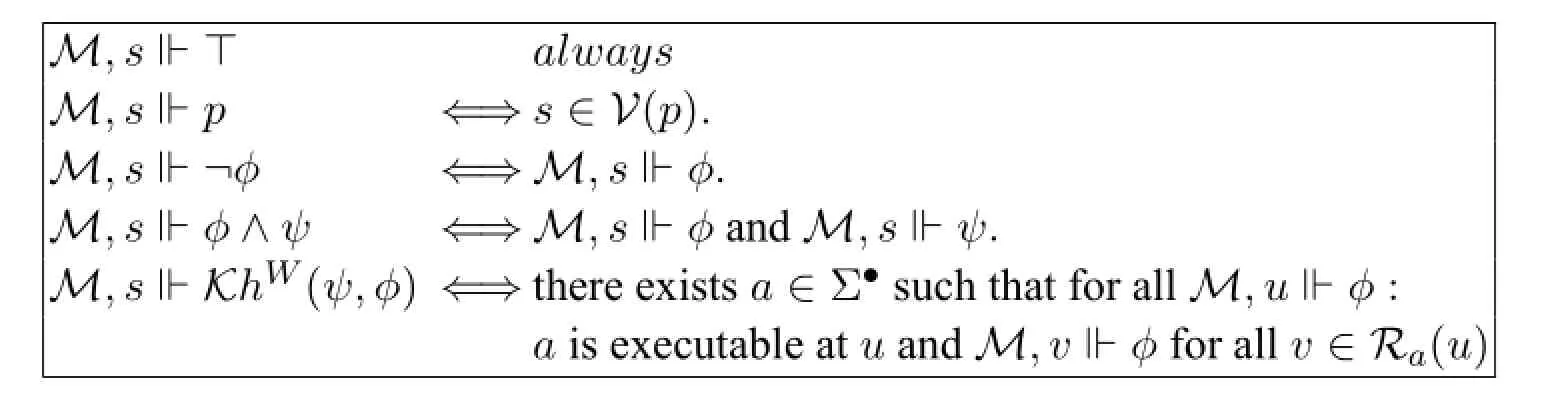
M,s⊩⊤alwaysM,s⊩p⇐⇒s∈V(p).M,s⊩¬φ⇐⇒M,s⊩φ.M,s⊩φ∧ψ⇐⇒M,s⊩φandM,s⊩ψ.M,s⊩KhW(ψ,φ)⇐⇒there existsa∈Σ●such that for allM,u⊩φ:ais executable atuandM,v⊩φfor allv∈Ra(u)

where Σ●=Σ∪{ϵ}.To sayφis valid w.r.t.the non-standard semantics,written⊩φ, meansM,s⊩φfor all pointed modelM,s.

In this non-standard semantics,the knowledge-how is interpreted almost the same with Moore’s first interpretation(I).The only difference is that the witness action for the knowledge-how might be epsilonϵ.Intuitively,it means that ifφis true on eachψ-state then we know how to achieveφgivenψtrivially by doing nothing.

LetM,s⊩Uφbe defined asM,u⊩φfor allu∈S.It is easy to show that

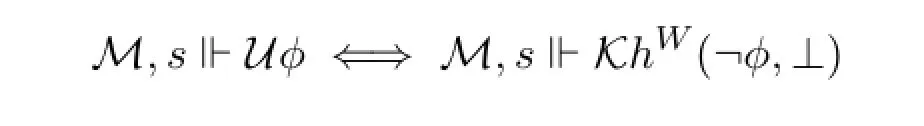
In order to show thatφis valid w.r.t.the standard semantics if and only ifφis valid w.r.t.the non-standard semantics,it follows by Theorem 1 and Theorem 2 that we only need to show that SKℍ is sound and complete w.r.t.the non-standard semantics.

SinceKhWis also a universal modality,it is easy to verify that SKℍ is sound w.r.t.the non-standard semantics.

Proposition 8If⊢φthen⊩φ.

Next we will show that SKℍ is complete w.r.t.the non-standard semantics. Given a consistent formulaφ,we will show thatφis satisfiable w.r.t.the non-standard semantics.

LetSub(φ)be the set of all sub-formulas ofφ.Let∼ψ:=χifχis a negation formula,otherwise,∼ψ:=¬χ.It is obvious that⊢¬ψ↔∼ψ.LetSub+(φ):=Sub(φ)∪{∼ψ|ψ∈Sub(φ)}.It is obvious that|Sub+(φ)|≤2|φ|where|φ|is the length ofφ.

Definition9(Atom)An atom ofSub+(φ)Aisa maximalconsistentsetwith respect toSub+(φ),if and only if,Ais a consistent subset ofSub+(φ)such that for eachψ∈Sub+(φ)ifA∪{ψ}is consistent thenA:=A∪{ψ}.We useA,B,Cto denote atoms.

Proposition 9If Γ is a consistent subset ofSub+(φ)then there exists an atomBofSub+(φ)such that Γ⊆B.

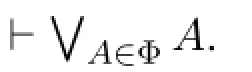
LetAbe an atom ofSub+(φ)such thatφ∈A.We define ΘA=A|KhW∪A|¬KhW.

Definition 10The modelMA=〈SA,ΣA,RA,VA〉is defined as follows.

·SA={Bis an atom ofSub+(φ)|(B|KhW∪B|¬KhW)=ΘA};

·ΣA={〈χ,ψ〉|KhW(χ,ψ)∈ΘA};

·p∈VA(B)⇐⇒p∈B,for eachp∈Sub+(φ).SAis non-empty becauseA∈SA.

Proposition 10ΘA⊢U∧ΘA

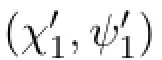
Proposition 11For eachψ∈Sub+(φ),ifψ∈Bfor allB∈SAthen ΘA⊢Uψ.

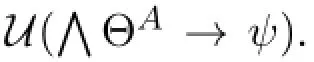
Proposition 12Givenχ∈Sub+(φ)andB∈SA,ifχ∈Bimplies that〈χ′,ψ′〉∈ΣAis executable atBthen we have ΘA⊢U(χ→χ′).

ProofAssume that ΘA∪{χ,∼χ′}is consistent.It follows that there existsC∈SAsuch that ΘA∪{χ,∼χ′}⊆C.It follows thatχ∈Cand〈χ′,ψ′〉is not executable atC.Contradiction.Therefore,ΘA∪{χ,∼χ′}is inconsistent.Thus, we have⊢∧ΘA→(χ→χ′).It follows by Rule NECU and Axiom DISTU that⊢U∧ΘA→U(χ→χ′).It follows by Proposition 10 that ΘA⊢U(χ→χ′).□

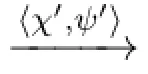
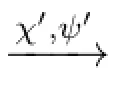
Proposition 14For eachψ∈Sub+(φ),MA,B⊩ψiffψ∈B.

ProofBoolean cases are trivial;we only focus on the case ofKhW(χ,ψ).

·a=ϵ.It follows thatM,C⊩ψifM,C⊩χ.By IH,we have thatχ∈Cimpliesψ∈Cfor allC∈SA.Therefore,we have ΘA∪{χ,¬ψ}is inconsistent.It follows that ΘA⊢χ→ψ.It follows by Rule NECU,Axiom DISTU,and Proposition 10 that ΘA⊢U(χ→ψ).It follows by Axiom EMPKh that ΘA⊢KhW(χ,ψ).Therefore,KhW(χ,ψ)∈B.

·a=〈χ′,ψ′〉∈ΣAand there is noC∈SAsuch thatχ∈C.It follows that ΘA∪{∼χ}is inconsistent.Thus,we have ΘA⊢¬χ.It follows by Rule NECU,Axiom DISTU,and Proposition 10 that ΘA⊢U¬χ,namely ΘA⊢KhW(χ,⊥).Since⊢U(⊥→ψ),it follows by Axiom UKh that ΘA⊢KhW(χ,ψ).Thus,we haveKhW(χ,ψ)∈B.

·a=〈χ′,ψ′〉∈ΣAandχ∈Cfor someC∈SA.It follows by IH that for eachχ∈B′we have〈χ′,ψ′〉is executable atB′.It follows by Proposition 12 that ΘA⊢U(χ→χ′).It follows by IH thatψ∈C′for eachC′∈SA

Proposition 15If⊩φthen⊢φ.

ProofWe only need to show that ifφis consistent thenφis satisfiable w.r.t.the non-standard semantics⊩.Ifφis consistent,it follows by Proposition 9 that there is an atomAofSub+(φ)such thatφ∈A.It follows by Proposition 14 thatM,A⊩φ.□

It follows by Propositions 8 and 15 that SKℍ is sound and complete w.r.t.the non-standard semantics⊩.Since SKℍ is also sound and complete w.r.t.the standard semantics⊨,we have the following lemma.

Lemma 2⊨φif and only if⊩φ.

Lemma 3Ifφis satisfiable w.r.t.the non-standard semantics,there is a modelMsuch thatM,s⊩φand|M|≤O(2|φ|).

ProofIfφis satisfiable w.r.t.the non-standard semantics,it follows by Proposition 8 thatφis consistent.Then by Definition 10,we can construct a modelMAwhereAis an atom ofSub+(φ)andφ∈A.It follows by Proposition 15 thatMA,A⊩φ. It is obvious that|MA|≤O(2|φ|).□

Theorem 3(Decidability)The problem that whetherφis valid w.r.t.the standard semantics is decidable.

ProofTo decide whetherφis valid w.r.t.the standard semantics,it follows by Lemma 2 that we only need to decide whetherφis valid w.r.t.the non-standard semantics.In other words,we only need to decide whether¬φis satisfiable w.r.t.the non-standard semantics.It follows by Lemma 3 that the problem of whether¬φis satisfiable w.r.t.the non-standard semantics is decidable.□

5 Conclusion and future work

In thispaper,we interpretthe knowing-how formulaKhW(ψ,φ)asthatthe agent has a weak conformant plan for achievingφgivenψ,and a weak conformant plan for achievingφ-states fromψ-states is a finite linear action sequence such that the performance of the action sequence at eachψ-state will always end up with aφstate,either successfully or not.Our interpretation of knowledge-how is weaker than the interpretation of[21]where knowledge-how is interpreted as that the agent has a conformant plan,but our interpretation is more realistic.We also present a soundand complete axiomatic system.It shows that this system is weaker than the system addressed in[21].We also show that this logic is decidable by reducing a standard decidable problem to a decidable problem w.r.t.the non-standard semantics.

One more interesting thing isthatthe canonicalmodelismuch more complicated even though the axiomatic system is weaker.Mainly,KhWformulas are realized by a two-step plan in our canonical model while they are realized by a one-step plan in the canonical model in[21].This also affords us some useful ideas about how to construct the decision procedure for the logic with tableau method.For example,for the tableau system of our logic,it is not enough to consider only one-step plans.

The non-standard semantics played a major role in this paper not only because it is the key step in the proof of the decidability but also because it reveals the fact that our formalization of knowledge-how is in principle the same with Moore’s first interpretation.It also shows that Moore’s interpretation does not contain the trivial case of knowing how to guarantee a state of affairs by doing nothing.

For future directions,we can express the existence of a weak conformant plan in the logic framework proposed in[27],where the existence of a conformant plan can be expressed by a formula.Moreover,we can study the knowing-how logic under fixed action set.In ourmodel,the action setΣisa partofthe model,butitis clearthat for different Σ we will get different logics.For example,if Σ is empty,KhW(ψ,φ)is equivalent toU(ψ→φ).If Σ is a singleton,the formulaKhW(p,q)∧KhW(q,r)→KhW(p,r)will be valid under our standard semantics.The more interesting thing is to compare the logic containing a finite Σ with the logic containing an infinite Σ.

Another exciting research field is the multi-agent version ofKhW.We can also considergroup notionsof“knowing how”.Especially,the contribute knowledge-how will be very useful.If you know how to achieve B from A and I know how to achieve C from B,we two together should know how to achieve C form A.Moreover,it also makes good sense to extend our language with public announcement operator.The update ofthe new information willresultin the change ofthe background information throughoutthe model,and thiswillaffectthe knowledge-how.We also conjecture that adding public announcement operator to our logic will make the expressivity strictly stronger.

[1]T.Ågotnes,V.Goranko,W.Jamroga and M.Wooldridge,2015,“Knowledge and ability”,in H.van Ditmarsch,J.Halpern,W.van der Hoek and B.Kooi(eds.),Handbook of Epistemic Logic,pp.543–589,College Publications.

[2]R.Alur,T.Henzinger and O.Kupferman,2002,“Alternating-time temporal logic”,Journal of the ACM,49:672–713.

[3]F.Belardinelli,2014,“Reasoning about knowledge and strategies:Epistemic strategy logic”,Proceedings of the Second International Workshop on Strategic Reasoning, pp.27–33,EPTCS.

[4]H.van Ditmarsch,J.Y.Halpern,W.van der Hoek and B.Kooi(eds.),2015,Handbook of Epistemic Logic,College Publications.

[5]J.Fan,Y.Wang and H.van Ditmarsch,2014,“Almost necessary”,Advances in Modal Logic,Vol.10,pp.178–196.

[6]J.Fan,Y.Wang and H.van Ditmarsch,2015,“Contingency and knowing whether”,The Review of Symbolic Logic,8:75–107.

[7]J.Fantl,2008,“Knowing-how and knowing-that”,Philosophy Compass,3(3):451–470.

[8]M.Ghallab,D.Nau and P.Traverso,2004,Automated Planning:Theory and Practice, Morgan Kaufmann.

[9]P.Gochet,2013,“An open problem in the logic of knowing how”,in J.Hintikka(ed.),Open Problems in Epistemology,The Philosophical Society of Finland.

[10]T.Gu and Y.Wang,2016,“‘Knowing value’logic as a normal modal logic”,Advances in Modal Logic,Vol.11,pp.362–381.

[11]S.Hart,A.Heifetz and D.Samet,1996,“Knowing whether,knowing that,and the cardinality of state spaces”,Journal of Economic Theory,70(1):249–256.

[12]A.Herzig,2015,“Logics of knowledge and action:Critical analysis and challenges”,Autonomous Agents and Multi-Agent Systems,29(5):719–753.

[13]A.Herzig,E.Lorini and D.Walther,2013,“Reasoning about actions meets strategic logics”,Proceedings of LORI 2013,pp.162–175.

[14]J.Hintikka,1962,Knowledge and Belief:An Introduction to the Logic of the Two Notions,Cornell University Press.

[15]W.van der Hoek and A.Lomuscio,2003,“Ignore at your peril—Towards a logic for ignorance”,Proceedings of AAMAS-03,pp.1148–1149.

[16]J.McCarthy,1979,“First-order theories of individual concepts and propositions”,Machine Intelligence,9:129–147.

[17]J.McCarthy and P.J.Hayes,1969,“Some philosophical problems from the standpoint of artificial intelligence”,Machine Intelligence,pp.463–502,Edinburgh University Press.

[18]R.C.Moore,1985,“A formal theory of knowledge and action”,in J.R.Hobbs and R.C.Moore(eds.),Formal Theories of the Commonsense World,Ablex Publishing Corporation.

[19]J.A.Plaza,1989,“Logics of public communications”,in M.L.Emrich,M.S.Pfeifer, M.Hadzikadic and Z.W.Ras(eds.),Proceedings of the 4th International Symposium on Methodologies for Intelligent Systems,pp.201–216.

[20]D.E.Smith and D.S.Weld,1998,“Conformant graphplan”,AAAI-98:Proceedings of the Fifteenth National Conference on Artificial Intelligence,pp.889–896.

[21]Y.Wang,2015,“A logic of knowing how”,Proceedings of LORI 2015,pp.392–405.

[22]Y.Wang,2017,“A logic of goal-directed knowing how”,Synthese,to appear.

[23]Y.Wang and J.Fan,2013,“Knowing that,knowing what,and public communication:Public announcement logic withKvoperators”,Proceedings of the 23rd IJCAI, pp.1147–1154.

[24]Y.Wang and J.Fan,2014,“Conditionally knowing what”,Advances in Modal Logic,Vol.10,pp.569–587.

[25]Y.Wang and Y.Li,2012,“Not all those who wander are lost:Dynamic epistemic reasoning in navigation”,Advances in Modal Logic,Vol.9,pp.559–580.

[26]G.H.von Wright,1951,An Essay in Modal Logic,Amsterdam:North Holland.

[27]Q.Yu,Y.Li and Y.Wang,2016,“A dynamic epistemic framework for conformant planning”,Proceedings of TARK XV,pp.298–318.

停下即完成：“知道如何”的弱逻辑

李延军
格罗宁根大学哲学系y.j.li@rug.nl

本论文针对王彦晶提出的“知道如何”的模态算子提出了一种新的语义。与原来的语义相比，我们的语义比较弱但是却更容易实现。根据该语义，主体知道如何从状态ψ到达状态φ当且仅当主体有一个有穷的线性动作系列使得执行该动作系列停止后的状态即是目的状态。这种弱化的新语义导致了一种弱化的逻辑。原来逻辑系统里面的组合公理在我们的新语义下不再有效。我们也给出了该逻辑的一个公理系统并证明了其可靠性和完全性。同时，我们也证明了该逻辑具有可判定性。

Received2016-06-07

*The author acknowledges the support from China Scholarship Council.The author thanks Yanjing Wang for telling the author the idea of the weak conformant plan and encouraging the author to write this paper.The author thanks Stipe Pandzic and Yuri David Santos for their helpful comments to make the paper more readable.The author is grateful to the two anonymous reviewers of this journal for their comments helping the author to improve the original work.Especially,one of them pointed out the interesting future direction of studying the logic under a finite action set.