Epistemic Logic with Functional Dependency Operator*

Yifeng Ding

Group in Logic and the Methodology of Science,UC Berkeleyyf.ding@berkeley.edu

Epistemic Logic with Functional Dependency Operator*

Yifeng Ding

Group in Logic and the Methodology of Science,UC Berkeleyyf.ding@berkeley.edu

.Epistemic logic with non-standard knowledge operators,especially the“knowingvalue”operator,has recently gathered much attention.With the“knowing-value”operator, we can express knowledge of individual variables,but not of the relations between them in general.In this paper,we propose a new operatorK fto express knowledge of the functional dependencies between variables.The semantics of thisK foperator uses a function domain which imposes a constraint on what counts as a functional dependency relation.By adjusting this function domain,different interesting logics arise,and in this paper we axiomatize three such logics in a single agent setting.Then we show how these three logics can be unified by allowing the function domain to vary relative to different agents and possible worlds.A multiagent axiomatization is given in this case.

1 Introduction

De reknowledge or in general non-standard knowledge in epistemic logic is attracting continuing attention.This line of research started from the very beginning of epistemic logic:Hintikka discussed a“knowing-who”operator in[4],and Plaza a“knowing-value”operatorKvin[5].However,it is the recent effort in providing formal semantics and axiomatizations of those non-standard knowledge operators,as outlined in[8],that layed a solid foundation for further investigation.Among all the non-standard knowledge operators axiomatized so far,the“knowing-value”,or equivalently the“knowing-what”operator,has received most attention,partly due to its mathematical elegance and partly because of its potential application in information security reasoning.Recent major development of thisKvoperator started with the axiomatization in[9,10],followed by the simplification of the semantics in[3] and the enrichment of the language through announcing values and propositions in [1,2].

Building on the above results about the“knowing-value”operator,this paper considers the knowedge of thefunctional dependencybetween variables,which is a natural extension of the knowledge of individual variables to the knowledge of relationsamong variables.The precise meaning of“knowing a/the functionaldependencybetween variables”is not easy to pin down and might be context sensitive,as illustrated by the difficulty to choose the correct article here:it is safe to say“knowing the value of a variable”since a variable can only take one value in the actual world(or any world),but there might be quite a lot functions,different from each other,yet all governing the relation between the same two variables in a set of possible worlds.We postpone furtherdiscussion to the lastsection,butitshould be intuitive that“functionality”is at least a minimal requirement,that is,to know any functional dependency between variablescandd,at least for any two possible worlds wherechas the same value,dshould also have the same value,however different from the value ofc.

Here one natural choice is to make functionality the only requirement of“knowing a/the functional dependency between variables”,and both[1,2]made this choice. The key intuition behind this choice is that,what matters in the end are the values of variables.Recall how implication in Heyting algebras for intuitionistic logic is defined:p→qis the weakest proposition such that if conjoined withpby taking conjunction,we get something stronger thanq,or in other words,we are able to inferq.In our knowing-value context,we might also be interested and only interested in knowing the values.Then,functional dependency ofduponcshould be interpreted as the weakest proposition such that if“conjoined”with the knowledge of the value ofd,we are able to infer the value ofc.

The weakest proposition possessing this bridging-the-gap property depends on how we interpret the word“conjoin”here.If it is taken to be the propositional conjunction,then what we get is again the propositional implicationKv(c)→Kv(d). If“conjoin”means revealing the actual value ofcto the agent,then[c]Kv(d)in[2] is an exact formalization.Model-theoretically speaking this means that functionality betweencanddholds on the set of possible worlds where the value ofcis correct, and consequently,once all possible worlds wherec’s value is wrong are eliminated, the value ofdbecomes fixed and hence known.If“conjoin”means to entertain the hypothesis that one of the epistemically possible values ofcobtains,then the functionality condition fromctodamong all possible worlds is the minimal requirement. This is equivalent toK[c]Kv(d),which says:I know that for all possible values thatccan take,once that is revealed to be the real value ofc,the value ofdwill also be known.In[1],this is exactly the semantics ofKcd.

Another famous work on dependency taking functionality as the only requirement is Dependence Logic.([6,7])The team semantics it uses for the dependence atom=(c,d)is exactly the functionality condition,though the teams in a model do not originate from an epistemic setting.

The semantics to be proposed in this paper will differ from the above pure functionality approach and willsubsume itasa specialcase.Butthe key inspiration comes from the basic strategy explained in[8]:pack an existential quantifier and a modal quantifier together in the form of∃x□φ(x).Under this pattern,the knowledge of the functional dependency of variablescanddis expressed as:there exists a functionfin a predetermined function domainFwhich works,in the sense thatd=f(c),in all epistemic scenarios.Thus,Fcan be seen as an agent’spriorknowledge aboutpossible functional dependency relations,and to know the dependency between variables is to find a possible function that works or explains all possibilities.To put it more colloquially,to know the functional dependency betweencanddis not simply to see that functionality holds between them,but also to see that the functional relation“make sense”.Let us useK f(C,d)to express this knowledge of functional dependency ofdupon a finite set of variablesC.

As argued above,when“knowing-dependency”serves as a tool for expressing potential“knowing-value”,we do not need a requirement stronger than functionality. But this is not always the case.Consider a typical scenario in information security: agent A receives an encrypted messaged=enc(c)from agent B.Ideally,A knows the value ofd,sayd=0,but knows nothing aboutc.So the epistemically possible worlds for A are

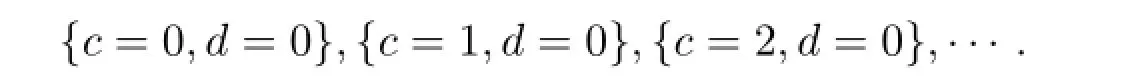
Certainly the functionality fromctodholds asdhas only one possible value.But agent A is apparently ignorant about the functional relationship between variablesdandc.The witness to the functionality here is the constant function 0,which is extremely unlikely to be the encryption function enc that B uses.So agent A would not in this case assert that she knows that the messagedshe receives is derived from the messagecthat B intends to send through some encryption:no encryption function she deems possible would allow all those possibilities.Thus,to claim the knowledge of the functional dependency ofdonc,we do need something more than functionality.With our operatorK f,we can useK fA({c},d)to express“A knows a functional dependency relation betweencanddthat is plausible in the information security context”,if we letFto be the set of all functions that is plausible in this context.

Thus,theK foperatorcan be used to modelscenarioswhere the value ofvariables in the realized world(the agent’s world)is not the sole concern of the agent.It might be that our agent does not want an inexplicable relationship between variables,or it might be that the agent requires that any functional dependency she knows to be applicable not only to her actual world but also to worlds metaphysically possible or worlds evolved in time,where somea priorirules preclude too strange functional dependency relationships.In the previous case,certainlydis known to A already,but the constantfunction thatwitnessesthe functionality there isnotlikely to be applicable to another round of message exchange.

In the rest of the paper,we first define the logic that incorporates knowledgeK,“knowing-value”Kvand“knowing-function”K foperators which we callLKVFand the corresponding base axiom system LKVF.Then we show how different domains of functions,viewed as a parameter ofLKVF,induce different sets of validities and axioms.Then all those cases will be put into a unified framework where a multiagentlogic with the same operators is axiomatized.In the last section,we will discuss further interpretations of“knowing a/the functional dependency between variables”and possible future work.

2 Preliminaries

2.1Syntax and Semantics of LKVF

Definition 1(Syntax)Given a countably infinite setPof propositional letters and a setQof the names of variables,the formulas inLKVFare defined by:

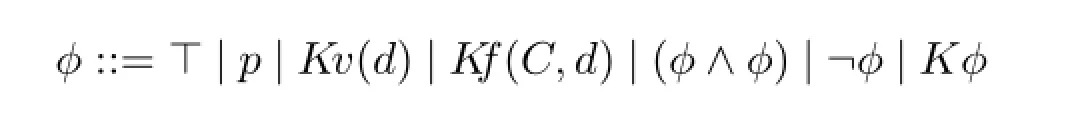
wherep∈P,d∈Q,andC⊆finQ.⊆finmeans a finite subset,possibly empty.

HereKv(d)is to be interpreted as“knowing the value ofd”,andKφ“knowing thatφis the case”.K f(C,d)says that the agent knows a functional dependency relationship fromCtod.By convention,we set⊥,(φ∨ψ),(φ→ψ)as¬⊤,¬(¬φ∧¬ψ),¬(φ∧¬ψ),and omit unnecessary parentheses.We also writeK f(c,d)as an abbreviation ofK f({c},d).

Aswe are considering single agentS5,no explicitaccessibility relation isneeded. So formally,a model is:

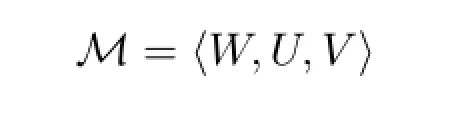
whereWis the set of possible worlds,U:W×P→{0,1}is the assignment for propositional letters,andV:W×Q→Gis the assignment for variables.For any finite subsetCofQ,we fix an order of the elements inCand defineV(w,C)=〈V(w,d)|d∈C〉.WhenCis empty,this degenerates into the unique empty tuple. We call this the joint assignment of variables inC,and whenever we have a function fromQtoG,if it is applied to a setC,we mean this joint assignment.Now the truth conditions are:

Definition 2(Semantics)

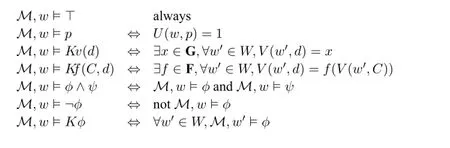
Here theKvoperator has the same meaning as that ofKvin[10]:Kv(d)means that under current epistemic uncertainty,the value ofdis certain.The new operatorK f(C,d)here means:the agent can find a function in the set of available functionsFthat can be used to explain the functional dependency relation betweenCandd. While both operators have the same structure in their semantics,namely∃□,the key difference here is that,ifKv(d)is true,only one value will be the witness,yet forK fthis is usually not the case.

To summarize,our logicLKVFextends the standard propositional epistemic logic by addingKv(d)andK f(C,d)to the language,adding a valuation of the variables to the models,and introducing a new function domainFas part of the logic. Now it has the following parameters:

·P:the set of propositional letters

·Q:the set of variable names

·G:the set of values that variables can take

·F:the set of functions that the agent deems possiblea priori.

All of them will have some effect on the validities ofLKVF,butPandQwill remain unchanged throughout the whole paper,since they can be viewed as part of the language.Gneeds to be large for completeness results,and we will specify how large it should be.Fwill change the validities inLKVFin an interesting way.Thus,it will be one of the main focuses of this paper.Later we show howFcan also be put into the models.

2.2Base Axiom System and Soundness Condition

As defined above,theK foperator expresses functional dependencies among variables and thus resembles the dependency relation in database theory.Using Armstrong’s three axioms in[11],we obtain this base system LKVF:

Here only the projectivity and transitivity axioms are used.The reason is that in our language the syntax ofK fallows only one variable to be dependent upon a set of variables,not a set upon a set.Thus,the additivity propertyK f(A,B)∧K f(A,C)→K f(A,B∪C)dealing with the second set of variables afterK fis not used and will follow from the properties of the conjunction if we defineK f(C,D)to be∧

d∈DK f(C,d).Then the augmentation axiom in the usual presentation of Armstrong’s axioms follows from additivity,projectivity,and transitivity.To show this, supposeK f(A,B).By projectivity,K f(A∪C,C)andK f(A∪C,A).Together with the assumptionK f(A,B),we haveK f(A∪C,B).So by additivity applied toK f(A∪C,C)andK f(A∪C,B),K f(A∪C,B∪C).

By convention,an empty conjunction is⊤.So when the setDin TRAN is empty,it actually saysK f(Ø,e)→K f(C,e)for allC⊆Q.And when the setCin VF is empty,it saysK f(Ø,d)→Kv(d).

We will discuss the axiomatizations of three different settings using a large,a small,and an intermediateFinLKVFrespectively.For them,we either use LKVF itself or add some other special axioms.To simplify repetitive work,here we give a condition onFinLKVFfor the soundness of LKVF:

Proposition1WhenFsatisfiesthe following,LKVF issound with respecttoLKVF:

·Foreveryi,j∈ℕsuch that0＜i≤jand functionf:Gj→G,f(x1,x2,...,

xj)=xiis inF.We denote this special projection function asidi,j.

·For everyf∈F,iffisn-ary withn≥1,then for everyg1,...gn∈F,f(g1(),...,gn())∈F.Namely,Fis closed under function composition.

ProofHere we only prove the soundness of the three less trivial axioms:

·By the first property ofF,PROJ holds.Ifd∈C,supposedappears inCas theith variable,thenV(w,d)=V(w,C)[i]always holds,and thus the witness ofK f(C,d)isidi,|C|.

·By the second property ofF,TRAN holds.The antecedent of this axiom states the existence offandgis in the second property.So the composition offandgis exists inF,which witnesses the consequent of TRAN.

·We want to show

LetCbe enumerated asc1,...,cnand suppose the antecedent in VF holds.

Further we haveK f(C,d),which means we have af∈Fsuch that

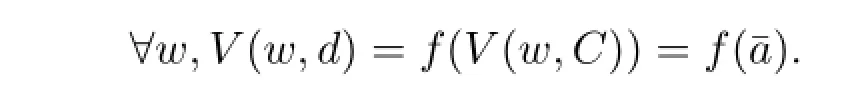
We will briefly mention howFis going to satisfy this soundness condition in all the following cases.

3 Full Domain of Functions

In this section,we deal with the case whereFis as large as possible,namelyF=∪{GGi|i∈N}.Now theK foperator degenerates into a functionality test,as all functions are allowed:

M,w⊨K f(C,d)⇔

This is true because once we have the right hand side true,we will obtain a partial functionfsatisfying∀w∈W,f(V(w,C))=V(w,d).And it is trivial to extend this partial function into a total function.

Now,ifM,w⊨Kv(d),then∀w1,w2∈W,V(w1,d)=V(w2,d),so the right hand side of the above truth condition holds,and consequently,K f(C,d)is true inM,w.This justifies the soundness of our new axiom in this case:whereC⊆finQ,possibly empty.We name this axiom EXT because it means that in this case every function onG,regardless of its meaning,can serve as a witness of the truth condition ofK f.Further,Fsatisfies the condition given in Proposition 1,so LKVF+EXT is sound.In the following,we prove that ifGis sufficiently large, then LKVF+EXT is in fact complete as well.

Given an arbitrary setAof formulas consistent in LKVF+EXT,the Lindenbaum lemma enables us to construct a maximal consistent set Γ such thatA⊆Γ. Now to build a model for Γ,we need to accompany this Γ by other maximal consistent sets(possible worlds).For example,if we have¬K f(C,d)in Γ,then we need two possible worlds on which the values ofCcoincide while the values ofdon them diverge.

To this end,we first define some useful sets.Given any maximal consistent set Γ,define

They collect all the propositional and the value knowledge respectively in Γ.For anyC⊆Q,we sayCisclosed underK finΓ if for allCf⊆finCandd∈Qsuch thatK f(Cf,d)∈Γ,we haved∈Cas well.Using axioms TRAN and PROJ,it is not hard to see that for allC⊆finQ,

is closed underK fin Γ andC⊆C+Γ.This can be seen as the dependency hull of the finite setC.An important observation is that,by axiom VF,ifK f(Ø,d)∈Γ,thenKv(d)∈Γ,soØ+Γ⊆KvΓ.Also,by axiom EXT,ifKv(d)∈Γ thenK f(C,d)∈Γ for allC⊆Q.SoKvΓ⊆C+Γfor allC⊆finQ,and in particularKvΓ⊆Ø+Γ.SoKvΓ=Ø+Γ.This motivates us to define the set of all finitely generated closed sets:

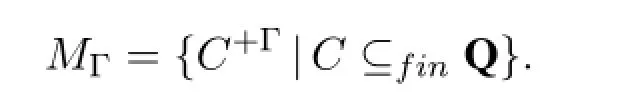
ClearlyMΓis non-empty,andKvΓ∈MΓ.Also,for allX∈Mwe haveKvΓ⊆X, so in other words,any finitely generated closed set contains all variables with known value.Then,we have the following disjoint decomposition ofQusingX∈MΓ:

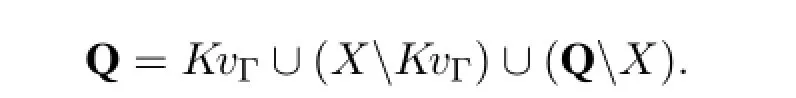
Intuitively,the values of the variables inKvΓmust hold fixed among all possible worlds;the values of the variables inXKvΓmust vary relative to those inKvΓin a uniform way to respect the functional dependencies among them;and the values of the variables inQXmust vary even when all values inXKvΓare fixed,since they are not determined byX.

For example,supposeQ={a,b,c,d},G=ℕ,and we want to model Γ whose knowledge consists only of:and their logical consequences such asK f(c,a).Then,when consideringX={a,b, c}={b}+Γ,we haveKvΓ={a},XKvΓ={b,c},andQX={d}.Among all possible worlds,the value ofamust be fixed;cmust change asc/∈KvΓ,but it should change together withbin case of violating functionality;anddhas to change even whenbtogether withcare fixed to refuteK f(b,d).Thus,one instantiation of this could be:

where the columns are possible assignments.For everyX∈MΓwhich collects all closed set of variables,we need such possibilities to take care of all formulas of the form¬K f(C,d)in Γ,because there will be oneX,namelyC+Γ,that separatesCandd.Then,the value ofdcan vary even when those ofCare fixed.

The reason we are using only finitely generated closed subsets ofQis that,when|Q|is infinite,the cardinality remains the same.Formally,definePf(Q)to be the collection of all finite subsets ofQ,then|Pf(Q)|=|Q|when|Q|≥ℵ0.Of course, whenQis finite,Pfcoincides withP,the ordinary powerset construction.Then,by the definition ofMΓ,|MΓ|≤|Pf(Q)|.

Now suppose|G|≥|Pf(Q)×{0,1}|,which is the largeness condition forGin this case,then there exists an injectiong:MΓ×{0,1}→G.Using thisgwe can define a functionVponMΓ×{0,1}×Qas follows:

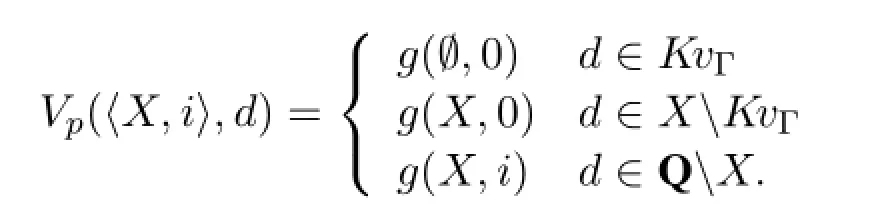
Notice how this satisfies the informal requirement,illustrated by the example above, over the values the variables in different regions should take.Whend∈KvΓ,its value is fixed tog(Ø,0).Whend∈XKvΓ,its value depends onXas a whole but nothing else,so allvariablesinXKvΓchange uniformly from whatthey are assigned byg(Ø,·).Whend∈QX,its value further depends oni,so will change even when the values of the variables inXare fixed.

Formally,this definition allows us to show:

Proposition 2For allC⊆finQ,d∈Q:

1.IfKv(d)∈Γ then

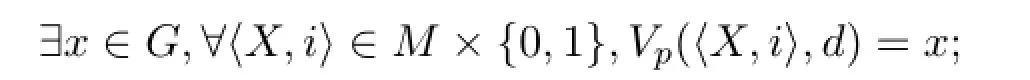
2.IfKv(d)/∈Γ then

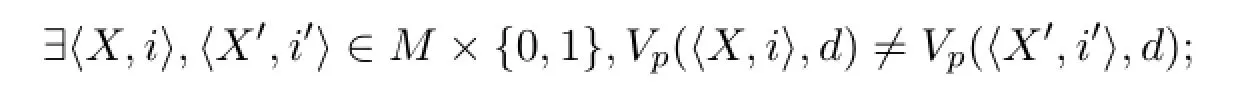
3.IfK f(C,d)∈Γ then

4.IfK f(C,d)/∈Γ then

ProofFor the first part,the witness isx=g(Ø,0)and can be verified easily.For the second part,as we observed before,KvΓ=Ø+Γ∈MΓ.Then,ifd/∈KvΓ,on〈KvΓ,0〉and〈KvΓ,1〉our valuation functionVpgives different values by the injectivity ofg.

For the third part,two cases are possible.IfC⊆KvΓ,thend∈KvΓby VF. ThenVpassignsg(Ø,0)todon all〈X,i〉,making the consequent of the implication to be proven true throughout.

Now supposeC/⊆KvΓand takec∈C(KvΓ)and〈X,i〉,〈X′,i′〉∈M×{0,1}such thatVp(〈X,i〉,C)=Vp(〈X′,i′〉,C).We first showX=X′by focusing on thisc/∈KvΓ.Sincec/∈KvΓ,by the definition ofVp,there existsj,k∈{0,1}such that

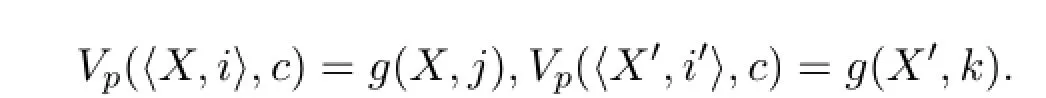
By the injectivity ofg,they are equal only if at leastX=X′.Based on this,ifi=i′then〈X,i〉=〈X′,i′〉and triviallydreceives the same value fromVp.

Ifi/=i′,recall that we assumedVp(〈X,i〉,C)=Vp(〈X,i′〉,C).For allc∈C, it follows thatc∈Xas otherwise the valuesVpgives tocdiffer oniandi′.HenceC⊆Xand by assumptionX∈MΓ,which meansXis closed.Thus,asK f(C,d)∈Γ,d∈Xas well.By definition,

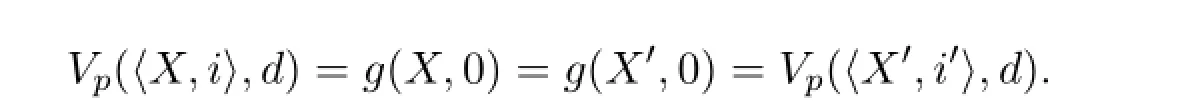
For the last part,we assume thatK f(C,d)/∈Γ.Thend/∈C+Γ.By the injectivity ofgand the fact thatC⊆C+Γ,

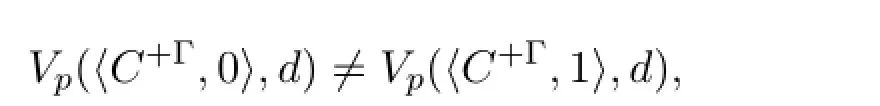
whereas□

The above proposition handles the knowledge and ignorance about values and functional dependencies.Now we need to combine it with a traditional completeness proof for epistemic S5 logic.Denote

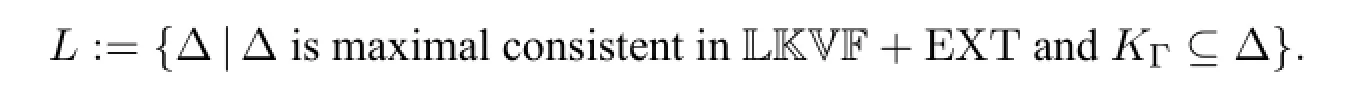
HereLis non-empty since by axiom T,KΓ⊆Γ so at least Γ∈L.Then we define a model on possible worldsW=L×MΓ×{0,1}:M=〈W,U,V〉where for every〈Δ,C,i〉∈W:

where[p∈Δ]isthe indicatorfunction ofthe statementp∈Δ,which evaluatesto 1 if the statementistrue and 0 otherwise.Here each possible world hasthree components: a maximally consistentsetwhich containsallformulastrue atthe world(truth lemma), a closed set of variablesCwhich is responsible for instantiating the ignorance of the values of variables inCunder the functional dependency constraint,and a number 0 or 1 which is responsible for instantiating the ignorance of the functionality property between variables inCand variables outsideC.

Now the goal is to show a truth lemma,i.e.,for all〈Δ,C,i〉∈W,φ∈Δ⇔M,〈Δ,C,i〉⊨φ.To this end,we first need the following simple observation.

Proposition 3For all Δ∈L,

·Kv(d)∈Δ⇔Kv(d)∈Γ,

·K f(C,d)∈Δ⇔K f(C,d)∈Γ,

·Kφ∈Δ⇔Kφ∈Γ.

ProofSimply use the axioms 4,5.For example,the third property follows from□

Proposition 4IfKφ/∈Γ,then there exists Δ∈Lsuch that¬φ∈Δ.

ProofA standard exercise using necessitation and axiom K.□

Now we can prove the truth lemma:

Lemma 1For all〈Δ,C,i〉∈W,φ∈LKVF,φ∈Δ⇔M,〈Δ,C,i〉⊨φ.

ProofBy induction onφ,with the following possibilities:

·φis a propositional letter or a boolean combination.This is standard.

·φ=Kv(d).Since Δ∈L,by Proposition 3,Kv(d)∈Δ⇔Kv(d)∈Γ.By Proposition 2,ifKv(d)∈Γ then

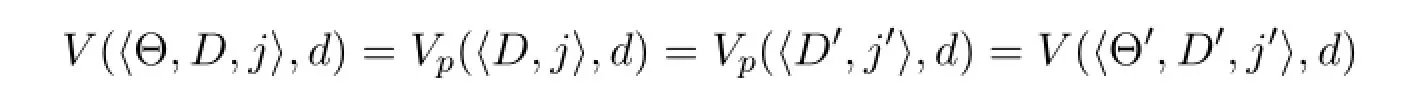
for all〈Θ,D,j〉,〈Θ′,D′,j′〉∈W.IfKv(d)/∈Γ,by Proposition 2 again,there exists〈D,j〉,〈D′,j′〉∈M×{0,1}such that

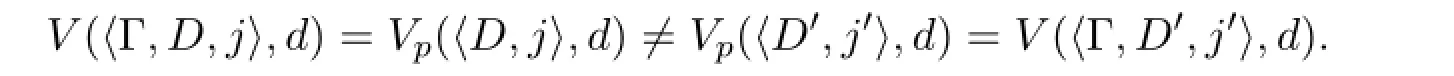
As such,

·φ=K f(D,d).Similar to the last one.By Proposition 3,K f(D,d)∈Δ⇔

K f(D,d)∈Γ.By Proposition 2,K f(D,d)∈Γ⇔M,〈Δ,C,i〉⊨K f(D,d).

·φ=Kψ.By Proposition 3,Kψ∈Δ⇔Kψ∈Γ.IfKψ∈Γ,thenψ∈KΓ, so for all〈Θ,D,j〉∈W,as Θ∈L,ψ∈Θ.By the induction hypothesis,M,〈Θ,D,j〉⊨ψ.Thus,M,〈Δ,C,i〉⊨Kψ.

On the other hand,ifKψ/∈Γ,by Proposition 4,there exists Θ∈Msuch that¬φ∈Θ.By the induction hypothesis,M,〈Θ,Ø,0〉⊨¬ψ.SoM,〈Δ,C,i〉/⊨Kψ.To sum up,Kψ∈Γ⇔M,〈Δ,C,i〉⊨Kψ.□

From this proposition,we know that for allφ∈Γ,M,〈Γ,Ø,0〉⊨φ.As the consistent setAwe chose at the very beginning is contained in Γ,M,〈Γ,Ø,0〉⊨A, which brings us:

Theorem1Given|G|≥|Pf(Q)×{0,1}|andF=∪{GGi|i∈N},LKVF+EXT axiomatizesLKVF.

4 Minimal Function Domain

In Proposition 1 we proved the soundness condition for LKVF.Notice that the minimal function domain that satisfies this soundness condition isIn this section,we consider the axiomatization of the validities ofLKVFwith thisF. Here,two axioms besides our base system LKVF are valid:

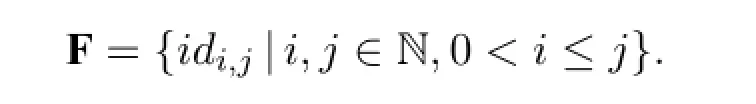
The validity of the first axiom is justified by:

and notice thatwhenC=Ø,itdegeneratestoK f(Ø,d)→⊥orequivalently¬K f(Ø,d), which is true because no zero-ary function exists inF.This also means that EXT is unsound in this case,because even ifKv(d)is true,K f(Ø,d)is false regardless.SoKv(d)→K f(C,d)is in general false.

The validity of the second axiom follows from

Thus,LKVF+CHOO+EQU is sound.Given these two axioms and the fact thatFconsists only of projection functions,K f(c,d)is actually talking about the equality ofc,dover all possible worlds,even though the value might not be known.This motivates the construction of the equivalence relation byK f(c,d)used below.

Now we turn to the proofofthe completenessof LKVF+CHOO+EQU.Again, given a consistent setA,our plan is that we first extend it to a maximal consistent set Γ,then deal with itsde reknowledge and propositional knowledge separately,and finally take their Cartesian product to obtain a model of Γ.

First,we partitionQinto equivalence classeswith equivalence relation∼defined by

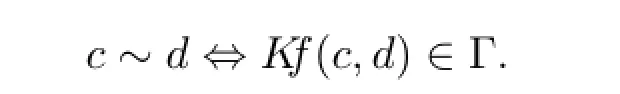
Its reflexivity,symmetry and transitivity follow from the axioms PROJ,EQU,and TRAN.Indeed,if we use theC+ΓandMΓconstruction,MΓwill contain precisely those partitions and their unions.Every maximally consistent set,or a“world”,naturally gives rise to such an equivalence relation onQ.

For everyc∈Q,define[c]={d|c∼d},and for everyC⊆Q,define [C]=〈[c]|c∈C〉,the collection of the equivalence classes which contain at least one of its elements.In particular,[KvΓ]=〈[c]|Kv(c)∈Γ〉.

Now,if|G|≥|Q|≥|[Q]|,then there will be two injections from[Q]toG,uandv,such that

For example,we can letube any injection and then make a rotation over the function values ofuon[Q][KvΓ]to obtainvin case ofQbeing finite,or letv(d)be the successor ofu(d)ford∈[Q][KvΓ]in case ofQbeing infinite(assuming it can bewell ordered).We do not need to seek more valuations of variables to prove the truth lemma in this case or to instantiate the ignorances of the knowledge about values in Γ.Any one of them is capable of refutingK f(C,d)/∈Γ and together they instantiateKv(d)/∈Γ.

DefiningVpas a function from{u,v}×QtoGbyVp(t,d)=t([d]),the following proposition is true:

Proposition 5For anyd∈Q,C⊆finQ:

1.ifKv(d)∈Γ,∃x∈G,∀t∈{u,v},Vp(t,d)=x

2.ifKv(d)/∈Γ,∃t,t′∈{u,v},Vp(t,d)/=Vp(t′,d)

3.ifK f(C,d)∈Γ,∃f∈F,∀t∈{u,v},f(Vp(t,C))=Vp(t,d)

4.ifK f(C,d)/∈Γ,∀f∈F,∃t∈{u,v},f(Vp(t,C))/=Vp(t,d).

ProofThe first two parts are immediate from the definition ofu,v:Kv(d)∈Γ⇔[d]∈[KvΓ]⇔u([d])=v([d])⇔Vp(u,d)=Vp(v,d).

For the third property,supposeK f(C,d)∈Γ and enumerateCbyc1,...,cj. By axiom CHOO and the maximality of Γ,there existsisuch thatK f(ci,d)∈Γ and thus[d]=[ci].Now,for everyt∈{u,v},Vp(t,C)=〈[c1],[c2],...,[cj]〉,so [d]=idi,j(Vp(t,C))and we see that the functional relation betweenC,disidi,j.

For the last one,supposeK f(C,d)/∈Γ.It follows that[d]/∈[C]because otherwise,[d]∈[C]and there existsc∈C,[d]=[c],henceK f(c,d)∈Γ.By axiom PROJ,K f(C,c)∈Γ,and then by axiom TRAN,K f(C,d)∈Γ,which contradicts the assumption.Again enumerateC=〈c1,...,cj〉.Sinceuis injective and[d]/∈[C],for allci∈C,u([d])/=u([ci]).Thus,for everyj-ary functionidi,j∈F,idi,j(Vp(u,C))=u([ci])/=u([d]).Actually we can usevhere as well. The reason we need both of them is that we need to instantiate¬Kv(d)ford/∈KvΓ.□

To build a model for Γ,define

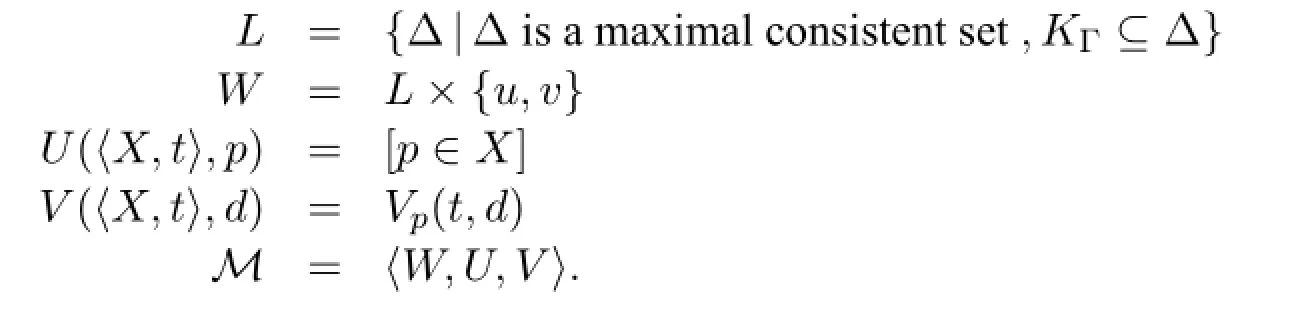
Then we have the following truth lemma:

Lemma 2For all〈Γ,t〉∈W,〈Γ,t〉⊨φif and only ifφ∈Γ.

ProofThe proof is similar to that of Lemma 1.The difference is that we need to use Proposition 5 instead of Proposition 2.□

The completeness ofLKVF+CHOO+EQU follows,so we conclude:

Theorem 2Given|G|≥|Q|,F=〈idi,j|i,j∈ℕ,0＜i≤j〉,LKVF+axiomatizesLKVF.

5 Intermediate Function Domain

In the previous two sections,we considered the minimal and the maximal function domains subject to our soundness condition.As we can see,in both cases the axiomatizations require some axioms besides the base system LKVF.And those axioms are not very intuitive if we intend to interpretK fas“knowing a/the functional dependency”.In this section,we show that we can construct a function domain such that ifFis set to it,LKVF will be complete and no extra axiom is needed.The construction is somewhat artificial but in the next section,we can view this as just one step of a completeness proof at a higher level.

The main difficulty here is to refute the axiom scheme EXT used in the axiomatization of the full function domain case.EXT is validated in that case because whenever the value of a variable is known,a constant function can be used to explain the functional dependency between it and any other variables in all epistemic possibilities.Thus,to refute this scheme as an axiom,we must make sure that the function domain encodes information more than just functionality so that we can refuteK f(c,d)even when functionality holds,such as whenKv(d)is true.The function domain to be constructed below will enable a suitably constructed model to refuteK f(C,d)without ever looking into the functionality condition.

To do this,we go to higher dimensions by assumingG=2Pf(Q),interpreted as functionsfrom the finite subsetsofQto{0,1}orasa ratherlong sequence indexed byPf(Q)where ateach index(dimension)Cwe can choose from{0,1}.Thisisactually only a size requirement,since so long as|G|≥|2Pf(Q)|,we can alwaysembed 2Pf(Q)intoGby an injection.For anyx∈GandC⊆finQ,we usex[C]to retrieve the image ofCunderx,which will be 0 or 1.Now we construct the intermediateF:

Definition 3LetFbe the collection of the functionsfsatisfying the following constraints:whereyisf(x1,...xn),for allC⊆finQ,

Alternatively,where

with max()=0,defineF=∪i∈ℕLmaxi.

Notice that the requirement is specified for all dimensions individually,and they do not interfere with each other.This allows us to do constructions and proofs for each dimension separately.

Now we can check that thisFsatisfies the soundness condition.Projection functions are all included inFbecause they all satisfy the above constraint:for anyC⊆finQ,eitherxi[C]=y[C]=1,where the antecedent and the consequent are both false,orxi[C]=y[C]=0,where they are both true.For compositionality,leth=f(g1,...gn).If all inputs tohare 0 at any dimensionC,then sinceg1,...gn∈F,they evaluate to 0 at dimensionC.Then all inputs tofare 0 at this dimensionC.So asf∈F,it evaluates to 0 as well.Thus,his inF.

To prove the completeness of LKVF with respect toLKVFwith this new function domainF,again the satisfiability of any maximal consistent set Γ is required, and the crucial step is still the construction of a set of valuations such that the formulas of the formKv(d),¬Kv(d),K f(C,d),and¬K f(C,d)in Γ are satisfied.Indeed, for this purpose we only need two valuations,a situation similar to that in the case of the minimal function domain.This is because when¬K f(C,d)∈Γ,we are refutingK f(C,d)not by a failure of functionality but by a failure of conformation toF.Breaking functionality requires at least two possible value assignments,but ifFsays no,a single possibility is too many.Recall theC+Γwe used in the previous two cases,which is defined as{d∈Q|K f(C,d)∈Γ}.Now we need to define a slightly differentMΓ:

This is the collection of all finitely generated closed sets plusKvΓ.We need this extra union since axiom EXT is not available now,which meansKvΓis not automatically contained in anyC+Γ,and it is quite possible thatKvΓis not finitely generated.But still,MΓhas a cardinality no larger thanPf(Q),since ifQis finite,Pf(Q)contains all subsets ofQ,and if infinite,Pf(Q)is also infinite and adding one more element into it does not increase its cardinality.Thus,there is still a surjectiongfromPf(Q) toMΓ.We can think of thisgasa pseudo(·)+Γfunction,and itdoes notmatterwhich surjection we use forg.Now we can specify the two valuations we need:

Definition 4Letgbe any surjection fromPf(Q)toMΓ.DefineV0,V1:Pf(Q)→Gsuch that for alld∈Q,C⊆finQ,

The use ofV0is to refuteK f(C,d)if¬K f(C,d)∈Γ,and the use ofV1is to refuteKvif¬Kv(d)∈Γ.Now we prove this in detail:

Proposition 6IfK f(C,d)∈Γ,then there existsf∈Fsuch that fori∈{0,1},f(Vi(C))=vi(d).If¬K f(C,d)∈Γ,then for allf∈F,f(V0(C))/=V0(d).

ProofTo prove the first claim,assume thatK f(C,d)∈Γ withCenumerated byc1,...,cn.We will construct a functionf∈Fthat works in bothV0andV1:for allD⊆finQ,V0(d)[D]=f(V0(C))[D]andV1(d)[D]=f(V1(C))[D].Obviously this construction should be done dimension by dimension.For anyD⊆finQ,the possibilities are:

·d∈g(D).Thus,by definition,V0(d)[D]=0.V1(d)[D]=0 as well since the only change happens whenD=KvΓ,and even in that case,only 1 turns to 0 and not vice versa.So we can definef(x1,...xn)[D]=0.ThenV0(d)[D]=f(V0(C))[D]andV1(d)[D]=f(V1(C))[D],regardless of whatV0(C)andV1(C)are.

·d/∈g(D).Sinceg(D)is closed andK f(C,d)∈Γ,C/⊆g(D).Findcp/∈g(D).Definef(x1,...xn)[D]=xp[D].This definition satisfies the requirement ofF.And it works forV0becausev0(d)[D]=V0(cp)[D]=1 (bothd,cpare outsideg(D)).It also works forV1because their values change to 0 together ifg(D)=KvΓ.

To prove the second claim,recallthatC+Γ={d|K f(C,d)∈Γ}isclosed underK fin Γ and containsCby axioms TRAN and PROJ.Now sinceK f(C,d)/∈Γ,d/∈C+Γ.Asgis a surjection fromPf(Q)toMΓ,there existsD⊆finQsuch thatg(D)=C+Γ.Thus,by the definition ofV0,V0(d)[D]=1,while for allc∈C⊆C+Γ=g(D),V0(c)[D]=0.HenceV0(d)[D]＞max(V0(C)[D]),which makes it impossible to find a functionf∈Fsuch thatf(V0(C))=V0(d).□

Proposition 7IfKv(d)∈Γ,thenV0(d)=V1(d).IfKv(d)/∈Γ,thenV0(d)/=V1(d).

ProofIfKv(d)∈Γ,thend∈KvΓ.Now for anyC⊆finQ,ifg(C)/=KvΓ,thenV1(d)[C]=V0(d)[C]by definition.Ifg(C)=KvΓ,V1(d)[C]=0,butV0(d)[C]=0 as well sinced∈KvΓ.Thus,V0(d)=V1(d).

IfKv(d)/∈Γ,d/∈KvΓ.Since we explicitly addedKvΓto Γ,KvΓ∈MΓ,and we can find aC⊆finQsuch thatg(C)=KvΓ.Then,using the definition ofV0andV1,we knowV0(d)[C]=1 butV1(d)[C]=0,becauseg(C)=KvΓand we assumedd/∈KvΓ.Thus,V1(d)/=V0(d).□

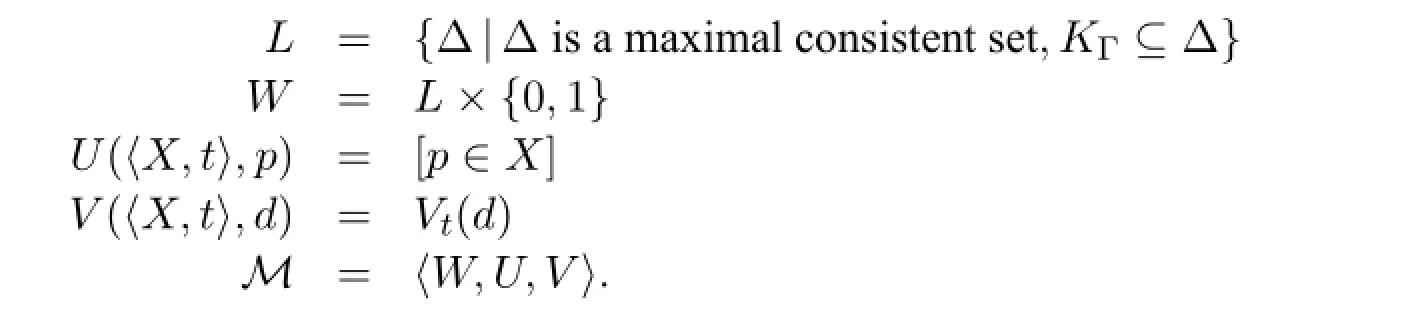
Based on the previous two propositions,we can build a model for Γ by definingWith a proof which is essentially the same as the proof of the truth lemma Lemma 1 in the full function domain case,using Propositions 6 and 7 instead of Proposition 2, we have:

Lemma 3For all〈Γ,t〉∈W,M,〈Γ,t〉⊨φif and only ifφ∈Γ.

M,〈Γ,0〉⊨Γ follows from this truth lemma.This finishes the completeness proof of the intermediate case,so we have:

Theorem 3Given|G|≥|2Pf(Q)|,F=∪i∈ℕLmaxi,LKVF axiomatizesLKVF.

Table 1:Choice of the function domain inLKVFand corresponding axiomatization

6 Unifying Logic

In all the previous settings,our logicLKVFtakes a function domainFas a parameter.This function domain is meant to be the set ofa prioripossible functions for functional dependencies over variables.But if this set ofa prioripossibilities is relative to the agents in discussion,then this set of functions should be variable over models instead of being part of the logic and fixed for all models.After all,an agent might hold different prior knowledge in different worlds.Also,the function domain constructed in the intermediate case is,while notnonsensicalforitsinteresting≤max structure,still somewhat artificial for its large dimension.If this function domain is part of the model,it is at the choice of the agent under discussion.

Indeed,if we put the function domain inside the definition of a model by setting

whereF:G→Gsatisfies the soundness condition that it contains all projection functions and is closed under function composition,Wis a set of possible worlds,Uisan assignmentfunction forpropositionalletters,andVisan assignmentfunction for variables,and we leave the semantics untouched,then the soundness and completeness of LKVF follow immediately from the results presented so far.UsingLKVF∗to denote the logic induced by the definition of the models above,we have:

Theorem 4LKVF is sound and complete with respect toLKVF∗when|G|≥|2Pf(Q)|.

ProofBecause for every model ofLKVF∗,its function domain satisfies the soundnesscondition Proposition 1,LKVF issound in allthe modelsofLKVF∗.Thisshows the soundness.

For any set Γ maximally consistent with respect to LKVF,take theFand the modelMconstructed in the intermediate function domain case.Then〈F,M〉⊨Γ and〈F,M〉is a model ofLKVF∗.Thus,every maximal consistent set is satisfiable.□

The proof above is a direct adaptation of the completeness result in the intermediate function domain case.In that case,we built a function domain that works for all maximal consistent sets in the sense that for all maximal consistent sets Γ,this same function domain can be used to refuteK f(C,d)/∈Γ when functionality cannot be used.This is actually the reason why the cardinality requirement forGis very high there.However,in the current setting where function domains are part of the models,the only thing needed is a method to build a function domain for each maximal consistent set Γ so that the functional dependency relation betweenC,dis rejected if¬K f(C,d)∈Γ.The difference will be made more clear in the following multiagent case.

6.1Multiagent Logic with Variable Function Domain

Given an index setAof agents,to accommodate multiple agents,the language is now expanded to

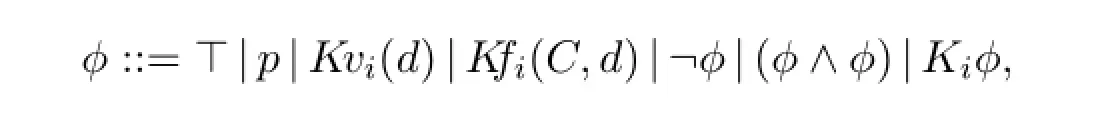
withp∈P,i∈A,d∈G,andC⊆finG.The only difference from the single agent language defined in Definition 1 is that now we have for each agentia separateKvi,K fi,andKi.

For semantics,a model is now defined as:

whereFiis intended to assign a collection of functional relationships that agentideems possiblea priorito all possible worlds inW.Thus,for allw∈W,i∈A,Fi(w)is required to include all projection functions and to be closed under function composition.∼iis the epistemic accessibility relation of agentiand is required to be an equivalence relation onW,the set of possible worlds(complete epistemic scenarios).Now sinceFiis supposed to be“prior knowledge”,it is also required that ifw∼iw′,thenFi(w)=Fi(w′).However,we are not assuming that the prior knowledge of any agent is public to other agents,so it is quite possible thatFj(w)/=Fj(w′) ifj/=i,even whenw∼iw′.In a nutshell,Fis are not common knowledge.

The semantic clauses are defined similarly with agent indices for knowledge sentences:

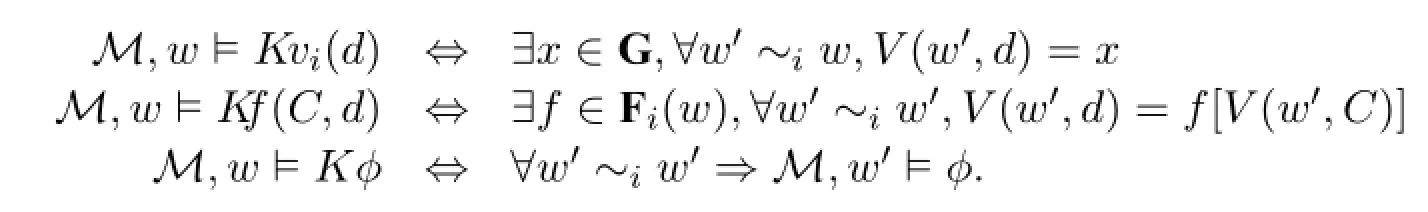
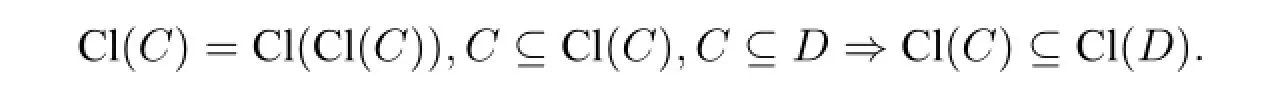
When a setC⊆QsatisfiesC=Cl(C),it is called a closed set.A classical result is that the collection of all closed sets under a closure operator forms a lattice〈L,∧,∨〉with

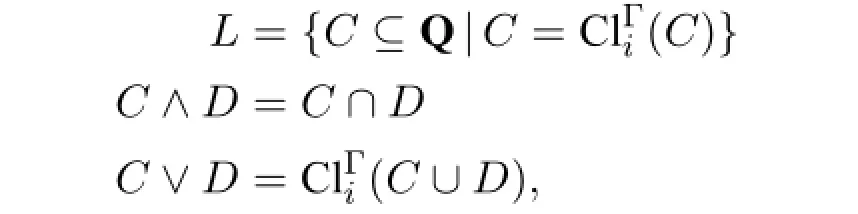
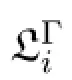
for allC⊆finQandd∈Q.

Forthe completenessproofto go through,there isagain a cardinality requirement forG:|G|≥|Q×{0,1}|,and without loss of generality,we identifyGwithQ× {0,1}.TheQpartwillbe used to constructthe function domainsand refuteK f(C,d), while the{0,1}part will be used for refutingKv(d).

Definition 6Given a maximal consistent set Γ and an agent indexi,we can construct the dependency lattice L and the corresponding h.Then defineFi(Γ)to be the collection of all functionsfonGwith any arityn∈ℕ such that:

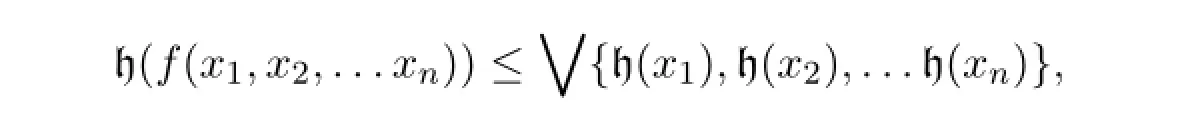
where≤is defined in L by a≤b⇔a∧b=b,or equivalently,a⊆b.The empty disjunction is the bottom element of L:Cl(Ø).

It is straightforward to see thatFi(Γ)is dependent only onKi,Γ.Then we need to verify the soundness conditions immediately:

Proposition 8For every maximal consistent set Γ andi∈A,Fi(Γ)contains all projection functions onGand is closed under composition.

ProofTake a projection functionf(x1,...xn)=xk.Then by the definition of join in a lattice,

since h(xk)∈{h(x1),···,h(xn)}.

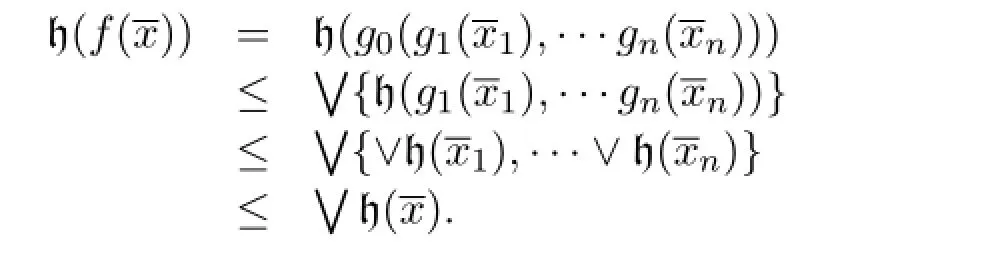
The next proposition shows why we use the dependence lattice to define the function domains for each agent.The proposition says that to makeK fi(C,d)true, we only need to make sure that functionality holds,and to makeK fi(C,d)false,we do not need to pay any special attention as the function domainFi(Γ)has already taken care of everything.

Proposition 9For everyσ∈2Q,definevσ:Q→G,d■→〈d,σ(d)〉.This means we restrictthe value ofd∈Qto be〈d,0〉or〈d,1〉.Now forevery maximalconsistent set Γ,i∈A,C⊆finQ,d∈Q,and Σ⊆2Q:

·if Σ satisfies the functionality condition forC,d,namely for allσ1,σ2∈Σ,σ1(C)=σ2(C)impliesσ1(d)=σ2(d),and ifK fi(C,d)∈Γ,then there existsf∈Fi(Γ)such that for allσ∈Σ,vσ(d)=f(vσ(C));

·ifK fi(C,d)/∈Γ then for allσ∈Σ and for allf∈Fi(Γ),vσ(d)/=f(vσ(C)).

ProofFirst notice that in the definition ofFi(Γ),the restriction actually forgets the second coordinate of the inputs and outputs.But it is the second coordinate that allσ∈Σ try to adjust.By definition,the first coordinates ofvσ(c)for allc∈Qare just themselves.So for allc∈Q,σ∈Σ,h(vσ(c))=Cl(c).

IfK fi(C,d)∈Γ,then(dropping the super and subscripts)d∈Cl(C).This means the same as{d}⊆Cl(C),which,by the fact that Cl is a closure operator,implies Cl(d)⊆Cl(Cl(C))=Cl(C).Then Cl(d)⊆Cl(C),which means h(vσ(d))≤Cl(C)in L forallσ∈Σ.Also,Cl(C)=∨{Cl(c1),Cl(c2),...Cl(cn)}=∨h(vσ(C)) for allσ∈Σ.So indeed h(vσ(d))≤∨h(vσ(C))in L.Together with the functionality assumed for Σ,this means mappingvσ(C)tovσ(d)simultaneously for allσ∈Σ is allowed inFi(Γ).Then we can extend this partial map to a map fromGntoGinFi(Γ).An easy solution is to do projection for all other possible inputs.

IfK fi(C,d)/∈Γ,thend/∈Cl(C)and hence Cl(d)/⊆Cl(C).If Σ is empty,the statement is trivially true.So assume Σ is not empty.Now take an arbitraryσ∈Σ. Then h(vσ(d))/≤∨h(vσ(C)),which violates the restriction onFi(Γ)ifvσ(C)is to be mapped tovσ(d).Thus,for allf∈Fi(Γ),vσ(d)/=f(vσ(C)).□

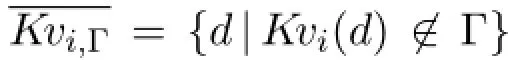
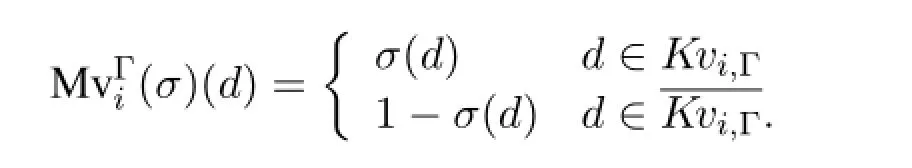
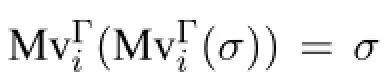
Equipped with the above definitions,the canonical model can now be defined:Definition 8(Canonical Model)Build a modelM=〈W,〈∼i〉i∈A,U,V,〈Fi〉i∈A〉as follows:

·W={〈Γ,σ〉|Γ a maximal consistent set,σ∈2Q},

·〈Γ,σ〉∼i〈Γ′,σ′〉iff

1.Ki,Γ=Ki,Γ′,which says that two worlds must share the same set of knowledge ofi,and

·U(〈Γ,σ〉,p)=[p∈Γ],

·V(〈Γ,σ〉,d)=〈d,σ(d)〉,or equivalently using notations introduced above in Proposition 9,V(〈Γ,σ〉)=vσ,

·Fi(〈Γ,σ〉)=Fi(Γ).

·∼iis an equivalence relation for alli∈A,

·Fi(〈Γ,σ〉)satisfies the soundness condition,

·if〈Γ,σ〉∼i〈Γ′,σ′〉thenFi(〈Γ,σ〉)=Fi(〈Γ′,σ′〉).

Because∼iis defined using equality,its reflexivity is easy to see.We need the two special properties of MvΓinoted right after the Definition 7 to show symmetry and transitivity.

Now the truth lemma in this case can be proven:

ProofUse induction onφ.The propositional letters and boolean combination cases are conventional.We focus on the knowledge cases.

φ=Kiψ.IfKiψ∈Γ,then by the definition of∼i,for all〈Γ′,σ′〉∼i〈Γ,σ〉,Ki,Γ=Ki,Γ′.Thus,ψ∈Ki,Γ′andKiψ∈Γ′.By axiom T,ψ∈Γ′,and using the induction hypothesis,M,〈Γ′,σ′〉⊨ψ.Thus,M,〈Γ,σ〉⊨Kiψby the semantic clause ofKi.

IfKiψ/∈Γ,then by a standard argument using axioms and the maximality of Γ,Ki,Γ∪{¬ψ}is consistent and expandable to a maximal consistent set Γ′.Then〈Γ′,σ〉∼i〈Γ,σ〉andM,〈Γ,σ〉⊨¬ψby the induction hypothesis.SoM,〈Γ,σ〉/⊨Kiψ.

φ=K fi(C,d).SupposeK fi(C,d)∈Γ.Then weshould firstshow thatthe functionality condition holds.For any〈Γ1,σ1〉,〈Γ2,σ2〉∼i〈Γ,σ〉,ifV(〈Γ1,σ1〉,C)=V(〈Γ2,σ2〉,C),then there are two possibilities

·C⊆Kvi,Γ.Then by axiom VF,d∈Kvi,Γas well,and by the argument in the previous case,V(〈Γ1,σ1〉,d)=V(〈Γ2,σ2〉,d)=〈d,σ(d)〉.

IfK fi(C,d)/∈Γ,then by Proposition 9 again,for every functionf∈Fi(Γ)=Fi(〈Γ,σ〉),there exists〈Γ′,σ′〉∼i〈Γ,σ〉such thatV(〈Γ′,σ′〉,d)/=f(V(〈Γ′,σ′〉,C)). Actually〈Γ,σ〉itself works here.Thus,M,〈Γ,σ〉/⊨K fi(C,d).□

7 Discussion and Future Work

First,we discuss the semantics of theK foperator.Obviously,whileKv(d) means that there is only one value fordto take,in general,the truth ofK f(C,d) does not force the set of possible functional dependency relations ofdonCto be a singleton.

It could be argued that the agent can nevertheless regard all those candidates as equivalent,because they must have exactly the same behavior over the partial domainP={V(w,C)|w∈W}.And things inG|C|but outside this setPare epistemically impossible.Thus,the behavior of functions onG|C|Pis something that our agent can and will ignore if situations epistemically impossible do not concern the agent. One example,also mentioned in the introduction,iswhen“knowing-value”isthe real objective ofthe agentand“knowing-dependency”only expressesthe agent’spotential to know more values.The semantics proposed in this paper allows adjustments toF, which might be a consequence of an agent’s concern about situations epistemically impossible,butnotnecessarily.And even ifitisthe case,the semanticsdoesnotshow howFis derived from what concerns of the agents.

It is not uncommon that epistemic possibilities are not the right place to stop when evaluating knowledge of functional dependency.Consider the following example:

I know the color of my hair.Therefore,I know the color of my hair functionally depends on the number of fingers I have.

This argument is very hard to swallow intuitively.Yet it is validated by the axiom EXT.Indeed,in the current setting of the semantics ofK f,to validate this,we only need to allow a moderate amount of constant functions in our function domain.The root of the problem is that,in a pure epistemic logic setting,if something is known, the agent has no access to other alternatives as knowledge is the only modality here, whereas in most realistic situations,even when something is known,we have modal access to some possibilities different from the known one.For example,possibilities in the future or past can be used to explain why the color of my hair is not really dependent on the number of fingers I have.And even when I have not and will not change the color of my hair,we can still use metaphysical possibilities:“the color of my haircouldbe different,regardless of how many fingers I have.”

Thus,it might be of interest to capture knowledge of functional dependency in anothermodality.To do thiswe can add a new modality□interpreted by a relationR. Then“knowing a/the functional dependency”can now be expressed by an operatorK f□with the following semantics:

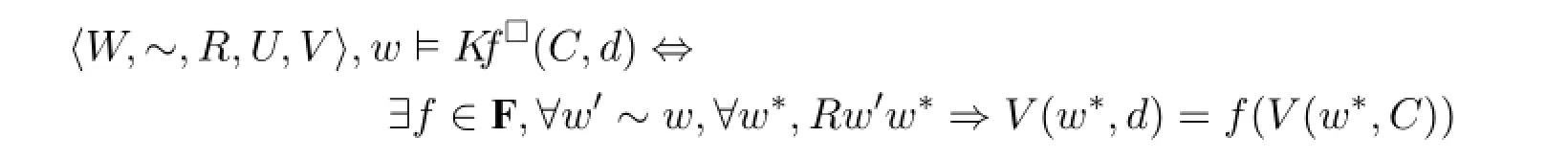
where∼is the epistemic indistinguishability relation.This definition still says that there exists a function that works for all epistemically indistinguishable worlds.But here“works”meansfcaptures the functional dependency ofduponCwith respect to another modality□which might be different fromK.

The choice ofRcan be arbitrary,but at least two interesting candidates are immediate:an equivalence relation to capture metaphysical possibilities and a linear or branching time relation used in temporal logics.A simple observation is that,if we still want a new version of VF,namely

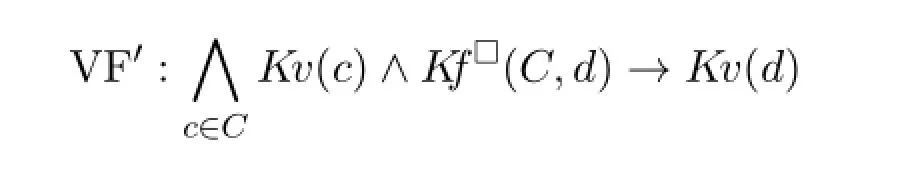
to be valid,we needRto be reflexive.Otherwise,the functionaldependency mightbe only talking about worlds far away from the actual world,though accessible throughR.Since the choice forRcan be flexible,there will be many interesting results to be discovered under this semantics.In particular,for the study of completeness,we might want to add more first order features to facilitate a proof more similar to its first order counterpart,a strategy successfully employed in[1].It might be desirable because,with two modalities,a direct construction of value assignments can be unmanageable.

Buta demanding readermay stillnotbe satisfied,aseven ifwe add a new modality,the choice of the functions could be nonunique again.This motivates another interpretation of knowledge of functional dependency,emphasizing even more the“knowledge”part:K f(C,d)says that the agent has gathered so much information that there is(almost)exactly one function that can be used to explain the data he/she has seen so far.Thus,knowledge appears only when there is only one possible or a few very plausible explanations.If there is no possible explanation in the sense that no function in the function domainFis applicable,or there are too many explanations,no knowledge is obtained.This sounds natural,but much more technically will be needed to formalize this:either a counting operator,or a probabilistic operator tracking the posterior distribution over the candidate explanations.

There are also interesting possible extensions of the framework given in this paper.For example,the multiagent case here assumed a no-interaction semantics. But once we require prior knowledge of possible functions to be available to otheragents,interesting interactions will appear.For example,supposeFjis known to agenti,i.e.,ifw∼iw′thenFj(w)=Fj(w′).Then the following is valid:

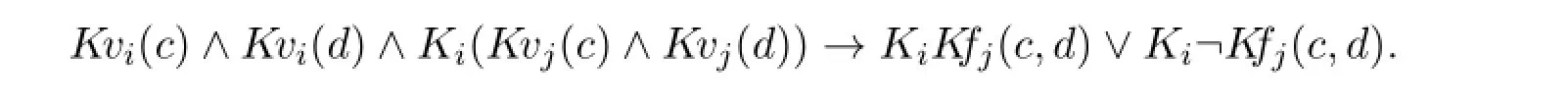
Intuitively this says that if agentiknows the values ofc,dand knows that agentjknows,then eitheriknowsthatjhasan explanation ofthe value ofc,doriknowsthatjdoesnothave one.The antecedentfixesthe value ofc,din allworldsaccessible first fromiand then fromj.Thus ifjfails or succeeds to explain this particular instance, agentiknows it.Stronger interactions will appear if we require all agents to share a single prior knowledge baseF,i.e.,for alli,w,Fi(w)=F.Then the following is valid:

This says that ifiknows the value ofc,dand knows thatjknows them,thenibeing able to explain this instance implies thatjcan explain it as well.To axiomatize these two cases,new axioms and techniques will emerge.Further,we can also add an operator that expresses knowledge about other agents’function domain.

Computationally,we see withouttoo much surprise thatthe finite modelproperty holds.For all the three single agent cases with a finite language,the required size ofGand the size of the model constructed can be explicitly computed.In the multiagent case,a standard filtration method can also be applied quite straightforwardly.Notice that in each of the three cases,the completeness proof requires a minimal size ofG. A natural question is whether we can bring down the size requirement by giving more economic completenessproofs.In particular,the double exponentialsize requirement in the single agent fixed intermediate function domain case seems to be too large, while the number of value assignments seems too small(just 2).We might be able to implement a trade-off here or a smarter lattice construction.

In summary,introducing knowledge aboutfunctionaldependency relationsbrings us ample new opportunities to extend the border of epistemic logic.There will be a lot more to achieve.

[1]A.Baltag,2016,“To know is to know the value of a variable”,Advances in Modal Logic,Vol.11,pp.135–155.

[2]J.van Ejick,M.Gattinger and Y.Wang,2017,“Knowing values and public inspection”,to appear in Proceedings of the Seventh Indian Conference on Logic and Its Applications.

[3]T.Gu and Y.Wang,2016,“‘Knowing value’logic as a normal modal logic”,Advances in Modal Logic,Vol.11,pp.362–381.

[4]J.Hintikka,1962,Knowledge and Belief:An Introduction to the Logic of the Two Notions,Ithaca N.Y.:Cornell University Press.

[5]J.A.Plaza,1989,“Logics of public communications”,in M.L.Emrich,M.S.Pfeifer, M.Hadzikadic and Z.W.Ras(eds.),Proceedings of the 4th International Symposium on Methodologies for Intelligent Systems,pp.201–216.

[6]J.Väänänen et al.,2008,“Modal dependence logic”,New Perspectives on Games and Interaction,4:237–254.

[7]J.A.Väänänen,2007,DependenceLogic—ANewApproachtoIndependenceFriendly Logic,Cambridge University Press.

[8]Y.Wang,2016,“Beyond knowing that:A new generation of epistemic logics”,in G.S. Hans van Ditmarsch(ed.),Jaakko Hintikka on Knowledge and Game Theoretical Semantics,to appear,Springer.

[9]Y.Wang and J.Fan,2013,“Knowing that,knowing what,and public communication: Public announcement logic withKvoperators”,Proceedings of the 23rd International Joint Conferences on Artificial Intelligence,pp.1139–1146.

[10]Y.Wang and J.Fan,2014,“Conditionally knowing what”,Advances in Modal Logic,Vol.10,pp.569–587.

[11]A.W.William,1974,“Dependency structures of data base relationships”,Information Processing 74:Proceedings of IFIP Congress 74,pp.580–583.

关于函数依赖关系的认知逻辑

丁一峰
加州大学伯克利分校逻辑与科学方法论小组yf.ding@berkeley.edu

对非经典知识，尤其是“知道是什么”的研究几乎是与对经典的认知逻辑的研究同时开始的，并且近来此类研究又吸引了诸多学者的注意。此种“知道是什么”算子能用来表达认知主体对个别变量的值的知识，但仅靠其自身却无法表达主体对变量之间的关系的知识。本文尝试提出一种K f算子来表达主体对变量间的函数关系的知识。不同于相关研究中类似的用于表达函数依赖关系的其它算子，这种K f算子的语义引入了一个先验函数域，用以表达认知主体对函数依赖关系的先验可能性的限制。我们将讨论该种语义下由不同的先验函数域引出的三种单主体逻辑，然后将其统一到一个逻辑当中并扩充为多主体逻辑。

Received2016-06-19

*The author would like to give special thanks to Malvin Gattinger and Wesley H.Holliday for their unreserved helpful comments.