Removing Your Ignorance by Announcing Group Ignorance: A Group Announcement Logic for Ignorance*

Jie Fan

College of Philosophy,Beijing Normal Universityfanjie@bnu.edu.cn

Removing Your Ignorance by Announcing Group Ignorance: A Group Announcement Logic for Ignorance*

Jie Fan

College of Philosophy,Beijing Normal Universityfanjie@bnu.edu.cn

.In this paper,we propose a group announcement logic for ignorance,which is an extension of the logic of ignorance with announcements and a group announcement operator for ignorance,expressing what is true after each agent in the group announces his/her own ignorance.We compare the relative expressivity of this logic and some relevant variations.We also investigate the frame definability issue of this logic.Besides,we present an axiomatization and demonstrate its completeness.

1 Introduction

Ignorance has been one of widely discussed topics in philosophy since Socrates, especially in epistemology.([28,58,59,18,24,10,19,61,27,43,50,44,51,52,23]) Butwhatdoesitmean by‘ignorance’?Justasno consensuswasreached among philosophers as to what is knowledge,there have been no consensus about the definition ofignoranceeither.Instead,at least three views have been proposed:the standard view,the new view,the logical view.1The terminology‘the standard view’was used in[44];‘the new view’was used in[51];while‘the logical view’is our term.According to the standard view,ignorance is merelya failure to know,i.e.negation of propositional knowledge.([58,18,27,43, 44,45,46])According to the new view,ignorance is equivalent tothe lack of true belief.([51,52,39])According to the logical view,ignorance isneither knowing nor knowing its negation.([36,33,34,57,21,22,48])

To our best knowledge,the first logical literature explicitly investigating ignorance is[33](see also its extended journal version[34]),where a logic of ignorance with ignorance operator as a sole primitive modality,is proposed and axiomatized with respect to the class of all frames.There,being ignorant of a propositionφisequivalent to neither knowingφnor knowing¬φ.This formalization has a long tradition in the literature of(non-)contingency logic,where contingency ofφmeans that bothφand¬φare possible.([42,14,35,37,62,21,22,20])Just as knowledge is the epistemic counterpart of necessity,ignorance is the epistemic counterpart of contingency.This relationship between contingency and ignorance enables us to translate technical results for contingency to results for ignorance,and vice versa,which though has been long neglected until[21,22].In this article we follow the definition of ignorance from[33].

As the negation of ignorance,‘knowing whether’is a useful expression in many fields,such asin AIforaction preconditionsand diagnostic planning applications([40, 56,55,53,4]),in economics for establishing a continuum of knowledge states([31, 29]),in scenariossuch asgossip protocolsand muddy children forformalizing higherorderepistemic reasoning([36,47,30,3]),and in linguisticsforanalyzing the embedding questions and inquisitive semantics([2,41,12,11,13]).Despite being definable with propositional knowledge(alias‘knowing that’),‘knowing whether’has some advantages,for example in succinctness([17]).For a detailed survey on‘knowing whether’,we refer to[60].We will define ignorance as a first class citizen,and take‘knowing whether’as the negation of ignorance.

With ignorance at hand,we can express various interesting statements.For example,“I am ignorant about your ignorance aboutp”,“If I am ignorant aboutp,then I am not ignorant about me being ignorant aboutp”etc.Ignorance may be removed by announcements.For instance,at first I was ignorant about whether it was raining in Nancy(q).But by Skype,Hans told me about the weather condition of that city and then my ignorance aboutqdisappeared.As another example,suppose Jay submitted a paper to a conference a couple of months ago and he learns that his friendbalso submitted a paper.Now Jay wonders whether his submission is accepted.But it is embarrassing to ask directly the programme chair who has decisions about submitted papers.What can he do?Jay can ask the chair the following two questions:“Isb’s submission or mine accepted?”“Ifb’s submission is accepted,then is mine accepted too?”No matter whether the chair says‘Yes’or‘No’,Jay will know whether his submission is accepted and then his ignorance disappears.These scenarios can be modelled in the logic of ignorance with announcementthat([22])and also in the logic of ignorance with announcementwhether([15]).

Not only can announcing a fact remove agent’s ignorance,announcing one’signorancemay also remove another’s ignorance.For example,two facts(saypandq)are both true atthe actualstate,butan agent(say Anne)isonly ignorantaboutpand, another agent(say Bob)is only ignorant aboutq.By announcing her own ignorance, Anne can help remove Bob’s ignorance.In turn,by announcing his own ignorance, Bob can help remove Anne’s ignorance.Thus Anne has an ability to remove Bob’s ignorance,and vice versa.Hence,Anne and Bob hasan ability to remove each other’s ignorance.This scenario can be easily modelled in our new logic,as will be seen inExample 1.

For the same reason,a coalition may announce what it isignorantabout,to remove its ignorance.Consider the benchmark example of muddy children.Father says:“Atleastone ofyou hasmud on hisorherforehead.”And then:“Willthose who know whether they are muddy step forward.”If nobody steps forward,father keeps repeating the request.In this puzzle,supposem+1 children are muddy,then aftermannouncements of their ignorance(by nobody stepping forwardmtimes),the muddy children willremove theirprevious ignorance status.Normally,the puzzle has always been formalized in terms of public announcement logic.([16])However,it seems very natural to model the scenario from the perspective of the group announcement logic forignorance,in that it is about what is true after the coalition(the muddy children)announces its own ignorance,and by(possibly iteratively)announcing the ignorance of every member in the coalition about its own status,the coalition has an ability to remove its ignorance.This type of group announcement is a joint public action of a group,i.e.,the announcement of theignoranceof the group,rather than the knowledge.

In this paper,we proposea group announcement logic for ignoranceGALI, which is an extension of the logic of ignorance with announcements and a group announcement operator for ignorance,expressing what is true after each agent in the group announceshis/herown ignorance.Section 2 definesthelanguage and semantics ofGALI,which is a fragment of a much larger logic.Section 3 determines the expressive hierarchy forGALIand some related logics.We investigate the frame definability ofGALIin Section 4.In Section 5 we present a proof system forGALIand show its soundness.Section 6 demonstrates its completeness via some revisions of the method in the literature.We conclude with some discussions and future work in Section 7.

2 Preliminaries

Throughout the paper,we letPandAgbe,respectively,the set of all propositional variables and the set of all agents,and letGbe a finite subset ofAg.We use|G|

to denote the cardinal number ofG.The following is a list of the logical languages involved in this paper,with the left being their respective notation and the right their respective original sources,wherep∈Panda∈Ag.2Some notation herein is different from that in the literature.For instance,CLAandACLAwere used in[22]and[15],instead ofIgAandAIgArespectively.

Definition 1(Logical Languages)

Intuitively,Kaφmeans“agentaknows thatφ”,Iaφmeans“ais ignorant about whetherφholds”,[ψ]φmeans“afterevery announcementthatψ,φholds”,□φmeans“after every announcement that,φholds”,[?ψ]φmeans“after every announcementwhether ψ,φholds”,■φmeans“after every announcement whether,φholds”,[G]φmeans“after every announcement that the groupGcan truthfully make about itsknowledge,φholds”,and[Gi]φmeans“after every announcement that the groupGcan truthfully make about itsignorance,φholds”.Other connectives are defined as usual;especially,Kwaφ,〈ψ〉φ,♢φ,〈?ψ〉φ,♦φ,〈G〉φ,〈Gi〉φabbreviate,respectively,¬Iaφ,¬[ψ]¬φ,¬□¬φ,¬[?ψ]¬φ,¬■¬φ,¬[G]¬φ,¬[Gi]¬φ.WhenG={a}(resp.{a,b}),we simply write[a](resp.[a,b])for[{a}](resp.[{a,b}]).We also adopt the same notation forGi,i.e.,write[a](resp.[a,b])for[{a}i](resp.[{a,b}i]).In specific contexts,no confusion arises about which operator we are referring to.The notation for〈G〉and〈Gi〉are similar.The formulaKwaφis read“agentaknows whetherφholds”.

We will assume that readers are familiar with epistemic logic(EL)and public announcement logic(PAL).In the semantics of these logics,the accessibility relations have mostly been assumed to be equivalence relations,since knowledge is an epistemic notion.ButELandPALcan also be investigated in the absence of any condition.In this paper,we do not have constraints on the accessibility relations.

The logic of ignorance(Ig)is proposed in[33,34],with the ignorance operator as a single primitive modality.The logicIgis interpreted on arbitrary models,i.e.the accessibility relation has no specific properties.The results therein also apply to the multi-agent case.A proof systemIg∪{G4}for transitive ignorance logic is claimed to be sound and complete in[34].However,as demonstrated in[22],among many other results,Ig∪{G4}is unsound with respect to the class of transitive frames.A so-called‘almost definability’schemaIaψ→(Kaφ↔(Kwaφ∧Kwa(ψ→φ))), meaning thatKisalmostdefinable in terms ofKw,is presented in[21].

Public announcements can remove the ignorance of agents.ExtendingIgwith public announcements,we obtain the logicIgAof ignorance with announcements (that).This logic is finitely axiomatized in[22]by adding[φ]Kwaψ↔(φ→Kwa[φ]ψ∨Kwa[φ]¬ψ)to the usual reduction axioms.Now that we take the ignorance operatorIas a primitive modality,we instead adopt an equivalent reductionaxiom[φ]Iaψ↔(φ→Ia[φ]ψ∧Ia[φ]¬ψ).

In spite of natural application ofIgA,it is argued in[15]that‘announcements whether’may be more suitable than‘announcements that’in some sense.For example,not only announcing thatp,but announcing that¬premoves agents’ignorance aboutp;in other words,after announcing whetherp(depending upon the actual truth value ofp),agents will know whetherp.Because of that,the quantifier should be‘arbitrary announcement whether’rather than‘arbitrary announcement that’.But as convincingly explained in[15],‘announcement whether’and‘announcement that’are interdefinable,and the semantics of‘arbitrary announcement whether’and that of‘arbitrary announcement that’are equivalent,thusAIgAalso counts as an extension ofIgAwith the arbitrary announcement operator.This logic is more expressive thanIgA,and incomparable withPAL.AIgAis infinitely axiomatized in[15],with a crucial application of the‘almost definability’schema cited above.It is unknown whether there is a finitary axiomatization forAIgA.

Arbitrary public announcement logic(APAL)is proposed in[7,8],which is an extension ofPALwith a modality thatformalizeswhatistrue afterany announcement. It is known thatAPALis undecidable([25]),but it is unknown whether there is a finitary axiomatization for this logic:the finitary system given in[8]is unsound.3The finitary rules in the axiomatization ofAPALgiven in([8])are actually unsound([38]).Besides,the completeness proof for the infinitary system also given in[8]contains an error.The error has been corrected in[5],which was in turn simplified in[6].

Group announcement logic(GAL)is proposed in[1],which is an extension ofPALwith a modality that expresses what a group can achieve by jointly announcing the knowledge of its members,which bridges the topics of dynamic epistemic logic[16]and coalition logic[49].Similar to the case forAPAL,the finitary system forGALgiven in[1]is unsound;4The finitary ruleR([G])reported in[1]is unsound.This can be shown similarly to the proof of the unsoundness of the finitary ruleR(□)in[38].In that proof,Kuijer shows that[ˆKbp]□¬γ→[q]¬γis valid whereas[ˆKbp]□¬γ→□¬γis invalid,whereγ=p∧ˆKb¬p∧ˆKaKbp.Similarly,we can show that,inGAL,δ∧[ˆKbp][c]¬γ→[Kcq]¬γis valid whereasδ∧[ˆKbp][c]¬γ→[c]¬γis invalid,whereδ=KaKb(ˆKbp→KcˆKbp).In other words,we strengthen the antecedent of the implication(namely withδ),and we replace the quantifier□by the quantifier[c]and[q]by[Kcq].We thank Louwe Kuijer for communicating this proof to us.and also,the completeness proof for the infinitary system given in[1]contains an error,which can be easily fixed via the method in[6]. Thus the problem of finitely axiomatizingGALis also open.

As we illustrated with the example of muddy children puzzle in the introduction, it may be interesting to study the group announcement logic for ignorance(GALI), which is an extension ofIgAwith a group announcement operator[Gi]for ignorance expressing what a groupGcan achieve by jointly announcing theignoranceof its members.Although it is known that the ignorance operator is definable with knowledge,as we willsee,the group announcementoperator[Gi]forignorance isundefinable in terms of the group announcement operator[G](for knowledge).Also,asmuddy children puzzle shows,the action of‘nobody stepping forward’amountsto the announcementthat‘nobody knows whether he is muddy’,it may thus be more suitable in our setting to use‘announcement that’rather than‘announcement whether’.5On the other hand,Hans van Ditmarsch mentioned that the muddy children puzzle can also be modelled in terms of announcement whether.In detail,replace announcement that and group announcement(that)for ignorance inGALI,respectively,with announcement whether and group announcement whether for ignorance.In this new logic,every member in a group announceswhetherit is ignorant about something.

As claimed,we define the accessibility relations without any constraint.

Definition 2(Model and frame)Amodel Mis a triple〈S,{→a|a∈Ag},V〉, whereSisa nonempty set ofpossible worlds,each→afora∈Agis a binary relation onScalled accessibility relation,andVis a valuation assigning each propositional variable a set of worlds.Aframeis a model without valuation.

Sometimes we writes∈Mwhensis belong to the domain ofM,in this case we say(M,s)is apointed model.The basic frame properties(i.e.seriality, reflexivity,transitivity,symmetry and Euclidicity)are defined as usual,and we say a frame is a P-frame,if it satisfies the property P.We useKandS5 to denote the class of all models and the class of all equivalent(i.e.reflexive,transitive and symmetric) models,respectively.

Definition 3(Semantics)Given a pointed model(M,s)withM=〈S,{→a|a∈Ag},V〉,we define the truth of a formula at(M,s)as follows.

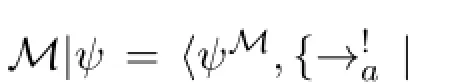
Formulaφistrueat(M,s),ifM,s⊨φ;φisvalid on M,writtenM⊨φ,ifφis true at every pointed model inM;φisvalid on F,writtenF⊨φ,ifφis valid on every model based onF;φisvalid,ifφis valid on every frame.

It is straightforward to derive the semantics of other modalities.For example,

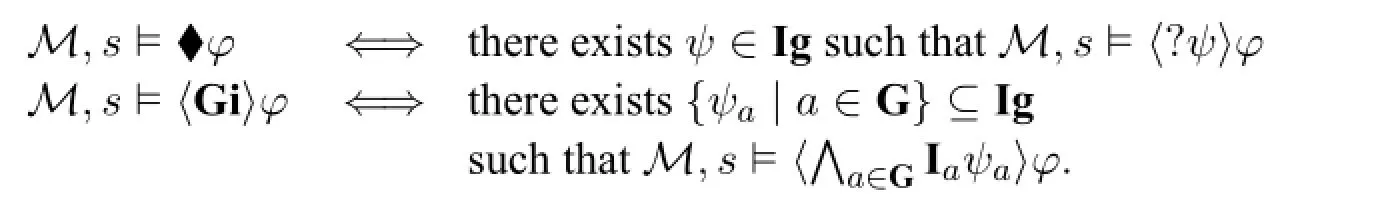
Intuitively,〈Gi〉φsays that after a(truthfully)public announcement of the ignorance of the coalitionG,φis the case.More succinctly,the coalition has an ability to make the goalφcome about,by announcing its ignorance.In the sequel,we will focus on group announcement logic for ignorance(GALI).

Note that the validities forGALIare not closed under uniform substitution.For example,the formula[q]p↔(q→p)isvalid,whereas one ofits instance[q]Kwiq↔(q→Kwiq)is not,as one may easily verify.

It is shown in[1,Prop.4]that forGAL,〈G〉p↔p,[G]p↔pandφ→〈G〉φare all valid.However,inGALI,we do not have the similar validities for our〈Gi〉and[Gi]operators.

Proposition 1We have the following validities and invalidities:

ProofThe validities are immediate from the semantics.For the invalidities,consider a modelMcontaining just two worldssandtboth of which are isolated,wherepis only true ats.ThenM,s⊨pbutM,s⊭〈Gi〉p(sinceM,s⊭Iaψfor allψ),and henceM,s⊭p→〈a〉p.Also,M,t⊨[a]pbutM,t⊭p,and henceM,t⊭[a]p→p.□

It is also shown in[1,Prop.13]that〈a〉Kbp↔〈b〉Kapis valid for all propositional variablesp.However,unfortunately this does not apply to itsGALIcounterpart:〈a〉Kwbp↔〈b〉Kwapis not valid.Intuitively,it says that two agents may have different capacities to remove each other’s ignorance about the same fact,if their initial status about that fact are different.

Proposition 2〈a〉Kwbp↔〈b〉Kwapis not valid.

ProofConsider the followingS5 model:

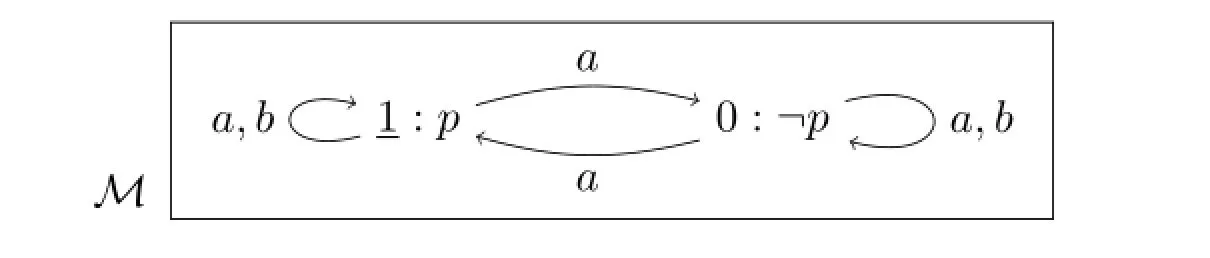
Sincebcan distinguish world 0 from world 1,we have thatM,1⊭Ibψfor anyψ∈Ig,thusM,1⊭〈b〉Kwap;however,since 1 and 0 both verifyIap,andM,1⊨Kwbp,it is easy to see thatM,1⊨〈Iap〉Kwbp,thusM,1⊨〈a〉Kwbp.□

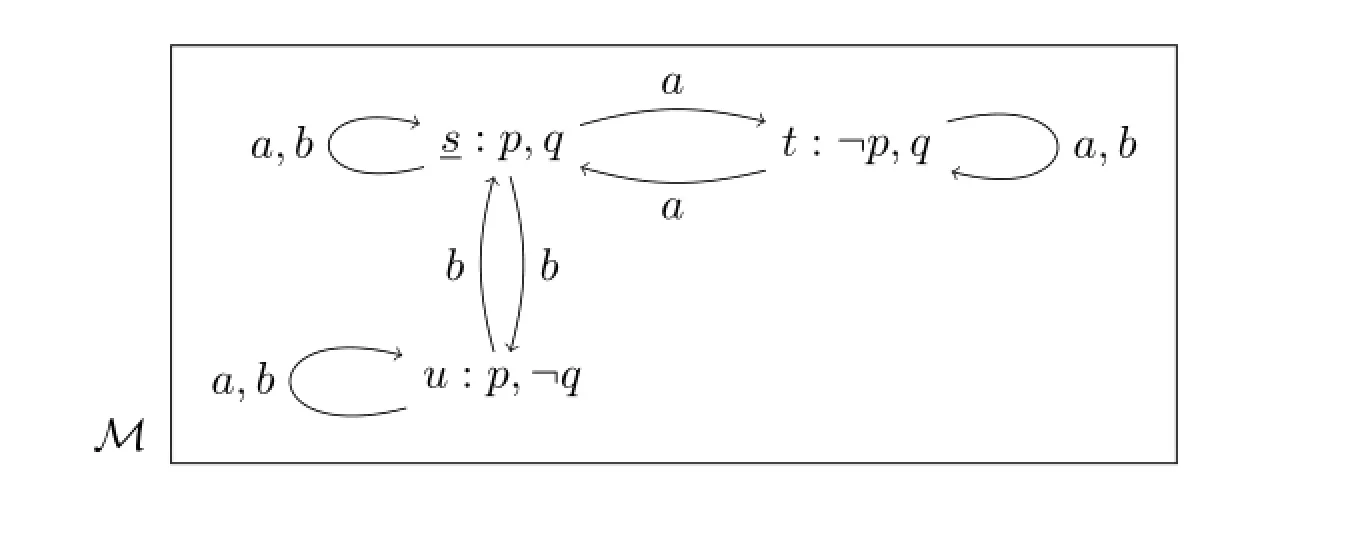
As noted in the introduction,announcing one’signorancemay also remove another’s ignorance.

Example1In theS5 modelM,itiseasy to show thatM,s⊨Iap∧Ibq∧〈b〉Kwap∧〈a〉Kwbq∧〈a,b〉(Kwap∧Kwbq),andM⊨[b]Kwap∧[a]Kwbq∧[a,b](Kwap∧Kwbq).

3 Expressivity

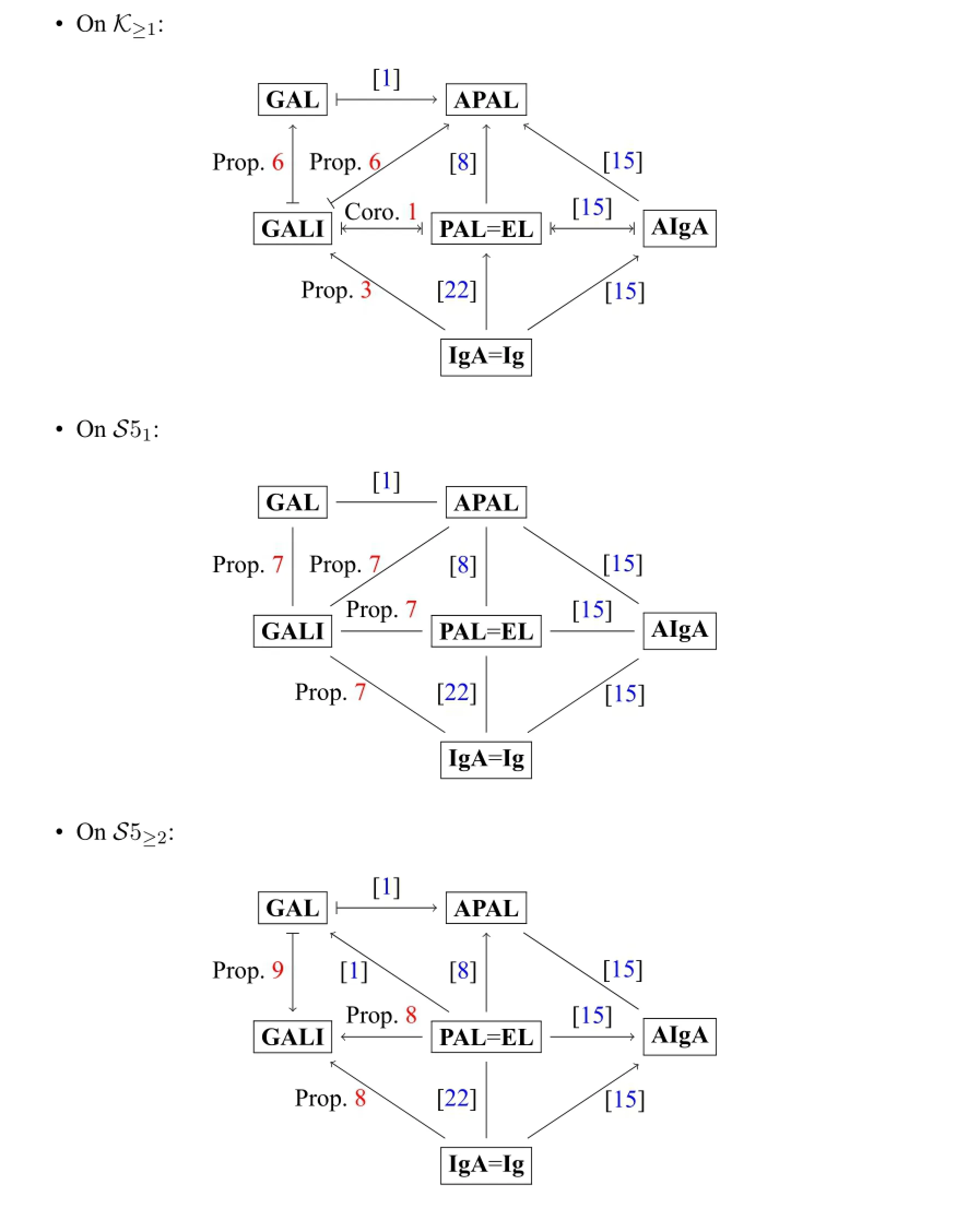
Figure 1:Relative expressivity of languages listed in this paper

3.1OnK≥1

Proposition 3(GALI＞Ig)GALIis more expressive thanIg.

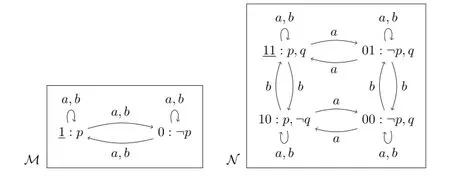
ProofClearly,GALIis an extension ofIg,thusGALI≥Ig.Now consider the formula〈a〉Kwap,and suppose,for a contradiction,that there exists aψ∈Igequivalent to it.Letqbe a propositional variable not occurring inψ.Consider the modelsMandNbelow(for the sake of simplicity,we omit the values of other propositional variables).

On the one hand,we observeM,1⊭〈a〉Kwap,since the announcement thatacan make is onlyIap(or equivalentlyIa¬p),after which the agentais still ignorant aboutp.On the other hand,we haveN,11⊨〈a〉Kwap,sinceN,11⊨〈Iaq〉Kwap. This is because in the modelN,the worlds verifyingIaqconsist of only 11 and 00, and in the updated model obtained by restricting to these two worlds,agentaknows whetherp.Thus there is aGALIformula〈a〉Kwapthat distinguishes(M,1)and (N,11).

Now we show that(M,1)and(N,11)cannot be distinguished by anyIgformulas not containingq,that is,M,1⊨φiffN,11⊨φfor allφ∈Igcontaining noq.This immediately follows because these two pointed models areKw-bisimilar restricted to atoms other thanq.6The notion ofKw-bisimilarity was introduced in[21],where it was called‘∆-bisimilarity’.Given a modelM=〈S,{→a|a∈Ag},V〉,we say thatZ⊆S×Sis aKw-bisimulationonM,ifZis nonempty,and if(s,t)∈Zanda∈Ag,then(i)sandtagree on all the propositional variables;(ii)for eachs′,ifs→as′ands→as1,s→as2for some(s1,s2)/∈Z,then there existst′such thatt→at′and(s′,t′)∈Z;(iii)for eacht′,ift→at′andt→at1,t→at2for some(t1,t2)/∈Z,then there existss′such thats→as′and(s′,t′)∈Z.We say that two pointed models(M,s)and(M′,s′)areKw-bisimilar,if there is a bisimulationZon the disjoint union ofMandM′such that(s,s′)∈Z.As a result,Igformulas are invariant underKw-bisimilarity.

Sinceψdoes not containq,we have thusM,1⊨ψiffN,11⊨ψ.Therefore we arrive at a contradiction,because we also haveM,1⊭〈a〉Kwap,N,11⊨〈a〉Kwapand the supposition thatψis equivalent to〈a〉Kwap.□

Proposition 4(EL/≥GALI)ELis not at least as expressive asGALI.

ProofObserve that the pointed models(M,1)and(N,11)in the proof of Prop.3 are also bisimilar restricted to atoms other thanq,and thus cannot be distinguished by anyELformula not containingq.□

Proposition 5(GALI/≥EL)GALIis not at least as expressive asEL.

ProofConsider the models below:

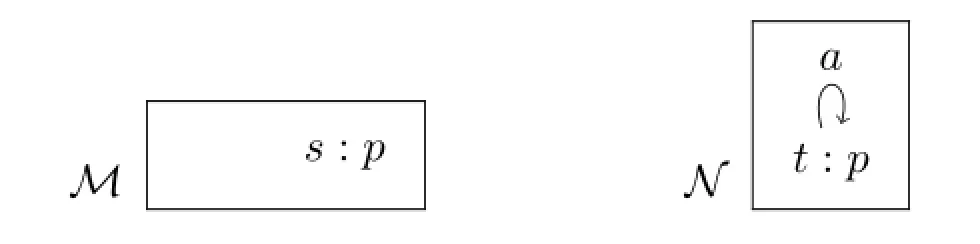
It is easy to show thatM,s⊨Ka⊥butN,t⊭Ka⊥.ThusELcan distinguish the two models.

However,the two models cannot be distinguished byGALI.That is,for anyφ∈GALI,we haveM,s⊨φiffN,t⊨φ.The proof proceeds with induction onφ.The boolean cases are trivial.

·CaseIaφ.Since bothsandthave at most one successor,M,s⊭IaφandN,t⊭Iaφ,thusM,s⊨IaφiffN,t⊨Iaφ.

1.1 幼苗的尖端被云母片一分为二后的生长情况 幼苗的尖端被云母片一分为二后，有不少资料认为幼苗在单侧光下直立生长。而事实是： 幼苗的尖端被云母片一分为二后，幼苗在单侧光下仍然会表现出向光性生长。

·Case[ψ]φ.SinceMhas only one worlds,we have:for anyψ,M|ψ=Mprovided thatM,s⊨ψ;similarly,N|ψ=Nprovided thatN,t⊨ψ.ThenM,s⊨[ψ]φiff(M,s⊨ψimpliesM|ψ,s⊨φ)iff(M,s⊨ψimpliesM,s⊨φ)iff(by IH)(N,t⊨ψimpliesN,t⊨φ)iff(N,t⊨ψimpliesN|ψ,t⊨φ)iffN,t⊨[ψ]φ.

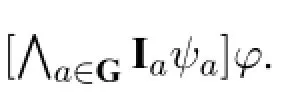
By Props.4 and 5,we have

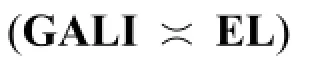
Proposition6(GALI/≥GAL,GALI/≥APAL)GALIisnotatleastas expressive asGALandAPAL.

ProofBy Prop.5,GALI/≥EL.SinceGALandAPALare both extensions ofEL, thusGALI/≥GALandGALI/≥APAL.□

We close this part with a conjecture.Item 1 can be supported by the following evidence:inGAL,only formulas of the form∧a∈GKaψacan be announced,whilethe announcements of the form¬Kaψa∧¬Ka¬ψa(equivalently,Iaψa)are not allowed,thus our[Gi]cannot be expressed inGAL.As a partial answer,onK≥2,GALis not at least as expressive asGALI,as will be shown in Prop.9 below.Combining this partial answer and Prop.6,we obtain:when more than one agent are considered,GALandGALIare incomparable onK.

Corollary 2OnK≥2,GALandGALIare incomparable.

1.(GAL/≥GALI)GALis not at least as expressive asGALI,

2.(GALI/≥AIgA)GALIis not at least as expressive asAIgA.

3.(AIgA/≥GALI)AIgAis not at least as expressive asGALI.

4.(APAL/≥GALI)APALis not at least as expressive asGALI.

3.2OnS5

Proposition 7(GALI=IgonS51)Let|G|=1.OnS5,GALIis equally expressive asIg.

ProofLetabe a unique agent.Given any formula[a]φ∈GALI,we have that⊨[a]φ↔φor⊨[a]φ↔⊤:onS5,alla-linked worlds agree onIaψfor allψ, thus for allS5 modelsMands∈M,we have thatM,s⊨[a]φiff(⋆)(for allψ∈Ig,M,s⊨[Iaψ]φ).If there is ana-successor ofsthat verifiesIaψ,in this caseM,s⊨Iaψand(M|Iaψ,s)isKw-bisimilar to(M,s),which implies that(⋆)is equivalent to thatM,s⊨φ,and hence⊨[a]φ↔φ.Otherwise,(⋆)holds vacuously, and hence⊨[a]φ↔⊤.□

Proposition 8(GALI＞IgonS5≥2)Let|G|≥2.OnS5,GALIis more expressive thanIg.

ProofSinceGALIis an extension ofAg,GALI≥IgonS5.We need only show thatIg/≥GALIonS5.Consider the followingS5 modelsMandN,and consider the formula〈b〉Kwap.Suppose,for a contradiction,that there is a formulaψ∈Igthat is equivalent to〈b〉KwaponS5.We may assume thatqdoes not occur inψ.Firstly,one may easily check that(M,1)isKw-bisimilar to(N,11)with regard toIgfor propositional variables not containingqand agentsa,b.ThusM,11⊨ψiffN,11⊨ψ.

Secondly,note thatM,1⊭〈b〉Kwap,as the announcement about the ignorance thatbcan make is onlyIbp(equivalentlyIb¬p),which does not change the modelMand agentais still ignorant aboutp.However,N,11⊨〈b〉Kwap,sinceN,11⊨〈Ibq〉Kwap.

We now get a contradiction and thus conclude the statement.□

Proposition 9(GAL/≥GALIonS5≥2)Let|G|≥2.OnS5,GALis not at least as expressive asGALI.

ProofConsider theGALIformula〈b〉Kwap,and suppose towards a contradiction that there is an equivalentGALformulaψ.We may assume thatqdoes not occur inψ.We willconstructtwoS5 pointed modelsthatcan be distinguished by〈b〉Kwapbut cannot be distinguished byψ,from which we will arrive at a contradiction.ConsiderS5 models below.

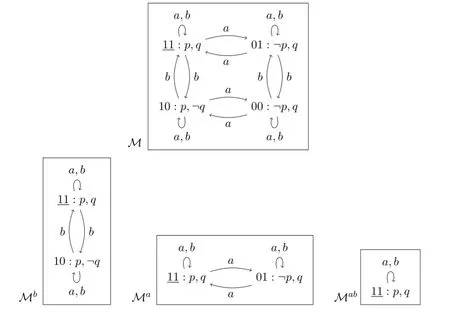
One may easily verify thatM,11⊨〈Ibq〉Kwap,thusM,11⊨〈b〉Kwap.However,it is easy to see thatMa,11⊭Ibφfor anyφ∈Ig,so we haveMa,11⊭〈b〉Kwap.ThusGALIcan distinguish between(M,11)and(Ma,11).

We will show that

(⋆)foranyGALformulaχwhich doesnotcontainq,M,11⊨χiffMa,11⊨χ.

To show this,first we observe thatM,11⊨χiffM,10⊨χ,M,01⊨χiffM,00⊨χ,M,01⊨χiffMa,01⊨χ,and alsoMb,11⊨χiffMab,11⊨χ.

The proof proceeds by induction onχ.The nontrivial cases are[χ1]χ2,[Ø]χ, [a]χ,[b]χ,and[a,b]χ.

·Case[χ1]χ2:

where(∗)follows since under the premise thatM,11⊨χ1,ifM,01⊨χ1, thenM|χ1=M,otherwiseM|χ1=Mb,(∗∗)follows from the induction hypothesis and aforementioned observations,and(∗∗∗)holds because under the premise thatMa,11⊨χ1,ifMa,01⊨χ1,thenMa|χ1=Ma,otherwiseMa|χ1=Mab.

·Case[Ø]χ:

·Case[a]χ:

·Case[b]χ:

·Case[a,b]χ:

We have thus completed the proof of(⋆).From(⋆)and the fact thatψdoes not containq,it follows thatM,11⊨ψiffMa,11⊨ψ,which is contrary to the supposition.□

It is known thatS5 models are alsoKmodels.As a corollary,when more than one agent are considered,GALisnotat least as expressive asGALIonK.

As previous,we close this part with a conjecture.

Conjecture 2OnS5≥2,

·GALIis not at least as expressive asGAL.

·GALIis not at least as expressive asAPAL.

·APALis not at least as expressive asGALI.

4 Frame Definability

It is shown in[62,Coro.4.4]and[22,Prop.3.8]that all the basic frame properties from Def.2 arenotdefinable inIg.SinceGALIextendsIg,it could have been that some of those frame properties are now definable.However,all of the five basic frame properties are also undefinable in the enlarged logicGALI.In this section we work on these undefinability results.

Given a set Γ ofGALIformulas and a classFof frames,we say that Γ definesFif for all framesF,F⊨Γ iffFis inF.In this case we also say that Γ defines the property ofF.If Γ is a singleton(e.g.{γ}),we always writeF⊨γinstead ofF⊨{γ}.A class of frames(or the corresponding frame property)is definable inGALI,if there is a set ofGALIformulas defining it.

Proposition 10The frame properties of seriality and reflexivity are undefinable inGALI.

ProofConsider the following frames,whereais an arbitrary agent inAg:Given anyφ∈GALI.Suppose thatF⊭φ,to showF′⊭φ.By supposition,there is anM=〈F,V〉and ansinMsuch thatM,s⊭φ.Define a valuationV′onF′such thatV(s)=V′(t).Similar to the proof of Prop.5,we can obtain thatM,s⊨φiff〈F′,V′〉,t⊨φ.Thus〈F′,V′〉,t⊭φ,and henceF′⊭φ.The converse is analogous. Therefore,F⊨φiffF′⊨φfor allφ∈GALI.

Ifseriality were defined by a setΓofGALIformulas,then asF′isserial,F′⊨Γ. SinceFandF′satisfy the sameGALIformulas,we obtainF⊨Γ,and thusFshould also be serial:a contradiction.Therefore,seriality is undefinable inGALI.

The argument for the undefinability of reflexivity is similar.□

Proposition 11The frame properties of transitivity,symmetry and Euclidicity are undefinable inGALI.

ProofConsider the framesFandF′below,whereais an arbitrary agent inAg:

Our objective is to show(♡):F⊨φiffF′⊨φfor allφ∈GALI.

Suppose thatF⊭φ.Then there existsM=〈F,V〉andxinMsuch thatM,x⊭φ.Define a valuationV′onF′such thatV(s)=V′(s′)andV(t)=V(t′). We now show that for allχ∈GALI,(i)M,s⊨χiff〈F′,V′〉,s′⊨χ,and(ii)M,t⊨χiff〈F′,V′〉,t′⊨χ.We proceed with a simultaneous induction onχ.We only consider the nontrivial cases[ψ]χ,[Ø]χand[a]χ.

·Case[ψ]χ.We have

Where(∗)follows since under the premise thatM,s⊨ψ,ifM,t⊨ψ, thenM|ψ=M,otherwiseM|ψ=〈Fs,V〉;(∗∗)follows due to(ii)and IH for(i)and the observation that〈Fs,V〉,s⊨χiff〈F′s′,V′〉,s′⊨χfor all

χ∈GALI;and(∗∗∗)follows because under the premise that〈F′,V′〉,s′⊨

·Case[Ø]χ.We have

·Case[a]χ.We have

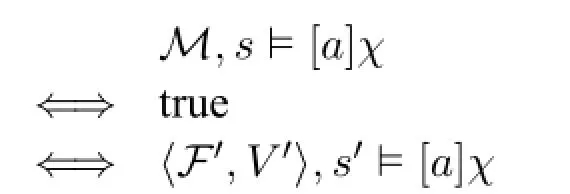
Where the first and second equivalences follow from the fact thatM,s⊭Iaψand〈F′,V′〉,s′⊭Iaψfor anyψ∈Ig.

Where the first and second equivalences follow from the fact thatM,t⊭Iaψand〈F′,V′〉,t′⊭Iaψfor anyψ∈Ig.

We have already shown(i)and(ii).Thusthere existsyin〈F′,V′〉such that〈F′,V′〉,y⊭φ,and henceF′⊭φ.

Similarly,we can show thatF′⊭φimpliesF⊭φ.Therefore the proof of(♡) is done.

We now show the undefinability as follows.Were transitivity or Euclidicity to be defined by a set Σ ofGALIformulas,asF′is transitive(resp.Euclidian),F′⊨Σ. From(♡),it follows thatF⊨Σ.This entails thatFshould also be transitive(resp. Euclidian).ButFis not transitive,sinces→atandt→asbut nots→as;neither isFEuclidian,ass→atands→atbut nott→at.Contradiction.

Were symmetry to be defined by a set Θ ofGALIformulas,asFis symmetric,F⊨Θ.From(♡),it follows thatF′⊨Θ.This entails thatF′should also be symmetric.ButF′is not,sinces′→at′but nott′→as′.Contradiction.□

5 Axiomatization and Soundness

In this section,we give a minimal axiomatization forGALI,and demonstrate its soundness with respect to the class of all frames.

First,we need the notion ofadmissible forms,which is originally from[26, pp.55–56],and then replaced with‘necessity forms’in[5,7,8,6].

Definition 4(Admissible forms)Whereχ∈GALIanda∈Ag,admissible formsθ(♯)are defined recursively as below.8Note that the difference between our constructIaχ→(Kwaθ(♯)∧Kwa(χ→θ(♯)))and the corresponding constructIaχ∧Kwaθ(♯)∧Kwa(χ→θ(♯))in[15,Def.14].But we should also note that the latter construct also works here,just as the former construct also works in[15].

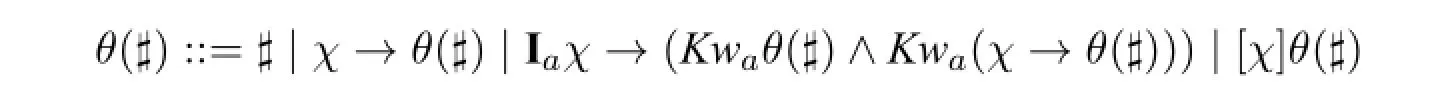
Here we appeal to the‘almost definability’schemaIaχ→(Kaφ↔(Kwaφ∧Kwa(χ→φ))).Recallthatin the contextofAPAL,the third inductive caseisKaθ(♯), see for example[8].According to the almost definability schema,under the premiseIaχ,Kaθ(♯)can be replaced with its equivalenceKwaθ(♯)∧Kwa(χ→θ(♯)).

Itiswellworth noting thateach admissible form has2noccurrencesof♯(n∈ℕ), due to the third construct.We define inductively a formula resulting from replacingthe occurrences of♯in admissible formsθwith any formulaφ,denoted byθ(φ),as follows.

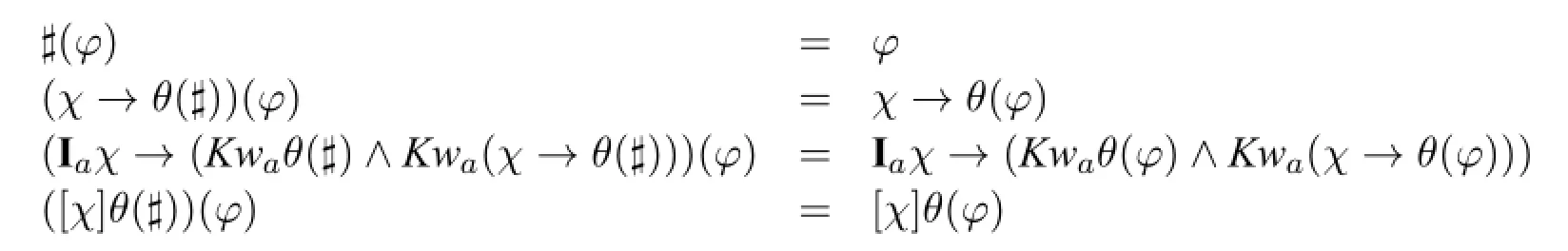
Definition 5The proof system GALI of the logicGALIcontains the following axioms and is closed under the rules below.

TAUT all instances of propositional tautologies

KwConKwa(χ→φ)∧Kwa(¬χ→φ)→Kwaφ

KwDisKwaφ→Kwa(φ→ψ)∨Kwa(¬φ→χ)

KwEquKwaφ↔Kwa¬φ

!ATOM[φ]p↔(φ→p)

!NEG[φ]¬ψ↔(φ→¬[φ]ψ)

!COM[φ](ψ∧χ)↔([φ]ψ∧[φ]χ)

!![φ][ψ]χ↔[φ∧[φ]ψ]χ

!I[φ]Iaψ↔(φ→(Ia[φ]ψ∧Ia[φ]¬ψ))

MP Fromφandφ→ψinferψ

NECKw FromφinferKwaφ

REKw Fromφ↔ψinferKwaφ↔Kwaψ

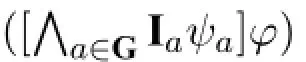
whereθis an admissible form

A formulaφis atheoremof GALI,notation⊢φ,ifφis either an instantiation of an axiom,or obtained by applying inference rules to axioms.We denote the set of all GALI theorems byThm.

It would be instructive to give some intuitions for the axioms and rules.Roughly speaking,KwCon tells us how to derive non-ignorance;KwDis tells us how to derive from non-ignorance;KwEqu states that knowing the truth value of a formula amounts to knowing the truth value of its negation;!I concerns about the interaction between announcement and ignorance:you are ignorant ofψafter the announcementφ,just in case that your ignorance of it also holds before the same announcement;GI says that group announcement for ignorance is stronger than specific announcement for ignorance,in that ifφholds after every announcement that the groupGcan truthfully make about itsignorance,thenφalso holds after every such kind of specific announcement;R(G)says that ifφholds after whatever simultaneous announcement for ignorance by each agent in a group,then it also holds after group announcement for ignorance by that group.

The resultbelow presentsa way ofremoving ignorance from some ignorance and non-ignorance,as can be seen from one ofitsequivalentsobtained via‘strengthening’the antecedent of the implication withIaχ.It will used in Prop.16.

Proposition 12For allφ,ψ,χ∈GALI,

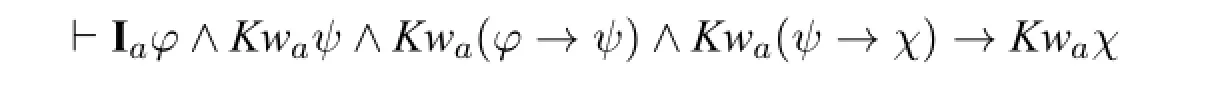
ProofWe can prove this as follows:

(i)Iaφ∧Kwa(φ→ψ)→Ia(ψ→¬φ)KwCon,KwEqu,REKw

(ii)Kwaψ∧Ia(ψ→¬φ)→Kwa(¬ψ→χ)KwDis

(iii)Kwa(¬ψ→χ)∧Kwa(ψ→χ)→KwaχKwCon

(iv)Iaφ∧Kwaψ∧Kwa(φ→ψ)∧Kwa(ψ→χ)→Kwaχ(i)−(iii)□

Proposition 13(Soundness of GALI)GALI is sound with respect to the class of all frames.

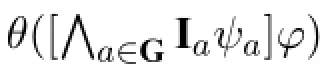
(∗) for all(M,s),

The proof proceeds with induction on the structure of admissible forms.The base case♯and the inductive casesχ→θ(♯)and[χ]θ(♯)follow from the semantics and induction hypothesis.For the caseIaχ→(Kwaθ(♯)∧Kwa(χ→θ(♯))),we have the following entailments(whereψGabbreviates{ψa|a∈G}):for all(M,s),

for allψG⊆Ig,M,s⊨Iaχ→

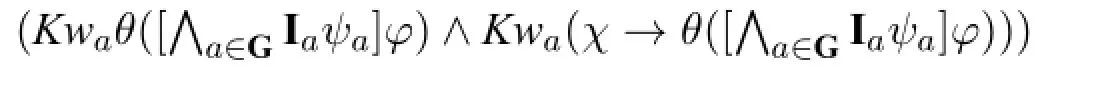
=⇒ifM,s⊨Iaχ,then for allψG⊆Ig,for allt∈M

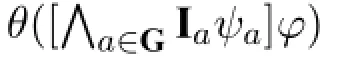
=⇒ifM,s⊨Iaχ,then for allt∈M

=⇒M,s⊨Iaχ→(Kwaθ([Gi]φ)∧Kwa(χ→θ([Gi]φ)))

The first and last entailments follow from the‘almost definability’schemaIaχ→(Kaφ↔(Kwaφ∧Kwa(χ→φ))).□

In the nextsection,we willdemonstrate the completenessof GALI,whose proof is based on a canonical model construction.However,in the truth lemma(Lem.2), the difficulty is to show the cases involving[Gi]φ,as we cannot apply induction hypothesis to the formulas in{ψa|a∈G}as indicated in the semantics.In order to solve the problem,we have to use{∧a∈GIaψa}φto‘encode’[Gi]φ(Prop.14) through a formula-based complexity measure(Def.6),and make use of the property being closed under R(G),which in turn leads to the notion of theory(Def.7).This is an adaption of the proof method in[6].

We close this section with a formula-based complexity measure and a‘simulation’of formulas of the form[Gi]φ.

Definition 6(≺)We define≺as a binary relation between formulas such that

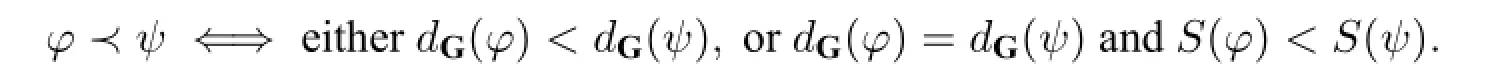
Where,dG(φ)is the[Gi]-depth ofφthat is a natural number,andS(φ)is the size ofφthat is a positive natural number,defined recursively as below.

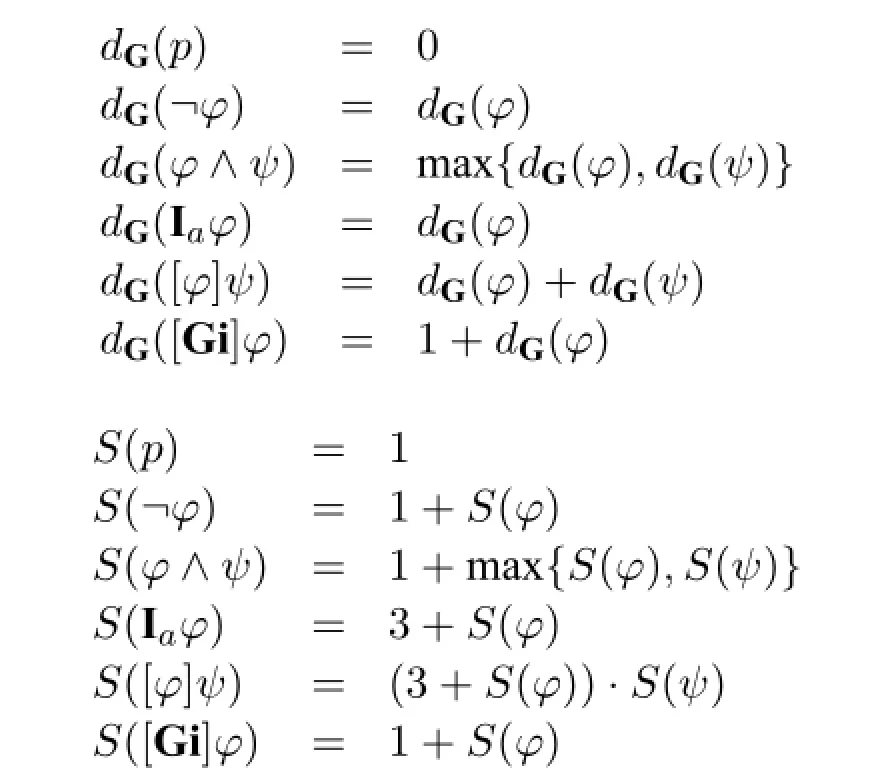
The case for the size of announcements in the above definition is different from [6,15].If we were to defineS([φ]ψ)to beS(φ)+3·S(ψ)as in[6,15],then we cannot provide thatψ→(Ia[ψ]χ∧Ia[ψ]¬χ)≺[ψ]Iaχin Prop.14,which is required when we prove the truth lemma.ForS([φ]ψ),3 is the least natural number giving us the proposition in question,in contrast to the complexity measure forPALin[16, Chap.7],where it is 4.

Furthermore,in the definition ofS(Iaφ),the number 3 is the smallest natural number giving us the next proposition.We can compute the depth and size of other constructs,for instance,dG(φ→ψ)=max{dG(φ),dG(ψ)},S(φ→ψ)=2+ max{S(φ),1+S(ψ)}.And ifφ∈Ig,thendG(φ)=0.Moreover,S(φ)≥1 for allφ.It is straightforward to show that≺is a well-founded strict partial order.

Proposition 14

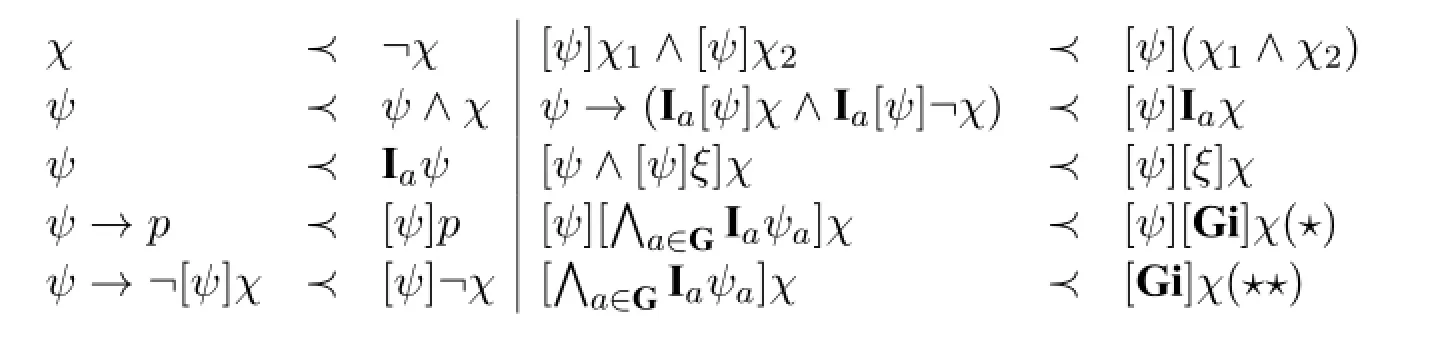
where in(⋆)and(⋆⋆),ψa∈Igfor a∈G.

ProofWe show the right column.We first compare the depths of formulas,if the depths are the same,then we proceed to compare their sizes.

·One may easily verify that dG([ψ]χ1∧[ψ]χ2)=dG([ψ](χ1∧χ2)).Moreover, S([ψ]χ1∧[ψ]χ2)=1+max{S([ψ]χ1),S([ψ]χ2)}.W.l.o.g.we assume that S(χ1)＜S(χ2),then this is equal to 1+S([ψ]χ2)=1+(3+S(ψ))·S(χ2), while S([ψ](χ1∧χ2))=(3+S(ψ))·(1+S(χ2)),thus S([ψ]χ1∧[ψ]χ2)＜S([ψ](χ1∧χ2)).Therefore[ψ]χ1∧[ψ]χ2≺[ψ](χ1∧χ2).

·One may easily verify that dG(ψ→(Ia[ψ]χ∧Ia[ψ]¬χ))=dG([ψ]Iaχ). Moreover,S(ψ→(Ia[ψ]χ∧Ia[ψ]¬χ))=10+3S(χ)+S(ψ)+S(ψ)·S(χ), whereas S([ψ]Iaχ)=9+3S(χ)+3S(ψ)+S(ψ)·S(χ).Since S(ψ)≥1,we have S(ψ→(Ia[ψ]χ∧Ia[ψ]¬χ))＜S([ψ]Iaχ).Therefore,ψ→(Ia[ψ]χ∧Ia[ψ]¬χ)≺[ψ]Iaχ.

·One may easily verify that dG([ψ∧[ψ]ξ]χ)=dG([ψ][ξ]χ).Moreover,S([ψ∧[ψ]ξ]χ)=4S(χ)+3S(ξ)S(χ)+S(ψ)S(ξ)S(χ),whereas S([ψ][ξ]χ)= 9S(χ)+3S(ξ)S(χ)+3S(ψ)S(χ)+S(ψ)S(ξ)S(χ).Since S(χ)＞0,we have S([ψ∧[ψ]ξ]χ)＜S([ψ][ξ]χ).Therefore[ψ∧[ψ]ξ]χ≺[ψ][ξ]χ.

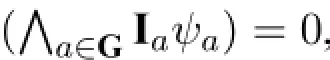
6 Completeness

In this section,we show that GALI is complete with respect to the class of all frames.The completeness proof is similar to that in[15],with some revisions.9We recall that our definition of admissible forms is different from[15],see footnote 8.Moreover, the definition of size has some interesting comparisons with that in[15]and some other literature,see Def.6 and the paragraph after it.

Definition 7(theory,consistent theory,maximal theory)A theory is a set of formulas such that it containsThmand is closed under MP and R(G).A theory isconsistent,if it does not contain⊥;a theory ismaximal,if for allφ,it containsφor¬φ.

Note thatwe define consistency foratheoryratherthan any setofformulas,since we need the condition of closure under R(G),which is indispensable in the proof of Lem.2.Consistency of a set Γ has always been defined just in case it does not entail falsum;in symbol,Γ⊬⊥.([9])One may verify that the notions of consistent theory and maximal consistent theory are,respectively,stronger than the notions of consistent set and maximal consistent set,since the latter notions are not necessarily closed under R(G).10However,as observed in[6,p.71],if the notion of consistent set is defined as inclusion in a consistent theory,then maximal consistent theories are equal to maximal consistent sets.

Defines+φ={ψ|φ→ψ∈s}.The following result can be similarly shown as in[15,Prop.24],where we need to use the closure ofsunder the admissible formχ→θ(♯).

Proposition15Letsbe a theory andφa formula.Thens+φisa theory containings∪{φ},ands+φis consistent iff¬φ/∈s.

Lindenbaum’s Lemma can be proved as Lem.4.12 in[8].

Lemma 1(Lindenbaum’s Lemma)Every consistent theory can be extended to a maximal consistent theory.

The canonical model has always been defined in a way such that the domain consists of all maximal consistent sets.However,as we noted before,maximal consistent sets are not necessarily closed under R(G),which is not what we want in the current setting(see the paragraph following Prop.13).Instead,we here define it for maximal consistent theories.The definition below is the same as the canonical model in[15],where the domain is the set of all maximal consistenttheories,in contrast to the set of all maximal consistent sets in[22].

Definition8(Canonicalmodel)The canonicalmodelfor GALI isMc=〈Sc,{→ca| a∈Ag},Vc〉where

·Scconsists of all maximal consistent theories for GALI.

–Iaχ∈sand

–For allφ,ifKwaφ∧Kwa(χ→φ)∈s,thenφ∈t.

·Vc(p)={s∈Sc|p∈s}.

Proposition 16LetIaφ∈sand Γa(s)={ψ|Kwaψ∧Kwa(φ→ψ)∈s}ands∈Sc.11Note that Γa(s)is different from,but equal to∆asin[15,p.95],given thatIaφ∈s.The reason for using Γa(s)rather than the original∆as,is because the new definition will simplify the proof of Prop.17.Then Γa(s)is a consistent theory.

ProofSupposeIaφ∈swheres∈Sc.We show that Γa(s)is a consistent theory.

·ContainsThm:given anyχ∈Thm,φ→χ∈Thm.Using NECKw we haveKwiχ∈ThmandKwi(φ→χ)∈Thm.Ass∈Sc,we getKwiχ∧Kwi(φ→χ)∈s,and henceχ∈Γa(s).

·Closed under MP:Assume thatψ,ψ→χ∈Γa(s),thenKwaψ∧Kwa(φ→ψ)∈sandKwa(ψ→χ)∧Kwa(φ→(ψ→χ))∈s(thus by REKw,Kwa(ψ→(φ→χ))∈s).By supposition and Prop.12,we inferKwaχ∧Kwa(φ→χ)∈s,and thenχ∈Γa(s).

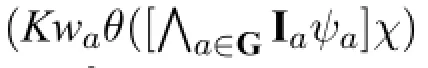
·Does not contain⊥:if not,i.e.⊥∈Γa(s),thenKwa⊥∧Kwa(φ→⊥)∈s, by Axiom KwEqu we can showKwaφ∈s,contrary to the supposition.□

Note that in the above proposition,the set Γa(s)is not maximal,which contains neitherφnor¬φ.

Proposition 17Lets∈Sc.

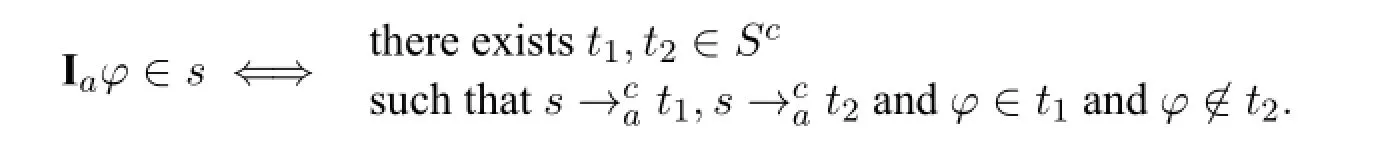
DefineΓa(s)={ψ|Kwaψ∧Kwa(φ→ψ)∈s}.By Prop.16,Γa(s)isa theory. Since neitherφnor¬φis in Γa(s),by Prop.15 both Γa(s)+φand Γa(s)+¬φare consistent theories and Γa(s)∪{φ}⊆Γa(s)+φand Γa(s)∪{¬φ}⊆Γa(s)+¬φ. By Lindenbaum’s Lemma,there existst1∈Scsuch that Γa(s)+φ⊆t1,and also there existst2∈Scsuch that Γa(s)+¬φ⊆t2.Therefore{ψ|Kwaψ∧Kwa(φ→ψ)∈s}∪{φ}⊆t1and{ψ|Kwaψ∧Kwa(φ→ψ)∈s}∪{¬φ}⊆t2,as desired.□

We tend to find our proof of‘Left-to-right’simpler than the corresponding part in[15,Prop.29].

Lemma 2(Truth lemma)For allφ∈GALI,for alls∈Sc,we have

ProofRecall that≺is a well-founded strict partial order between formulas.We show the statement by≺-induction onφ.In what follows we only show the cases involving[Gi]operator.Other cases can be shown as in[15,Lem.30],except that for each case,we use induction hypothesisforaformula,ratherthan forformulastherein.

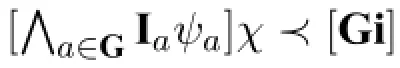
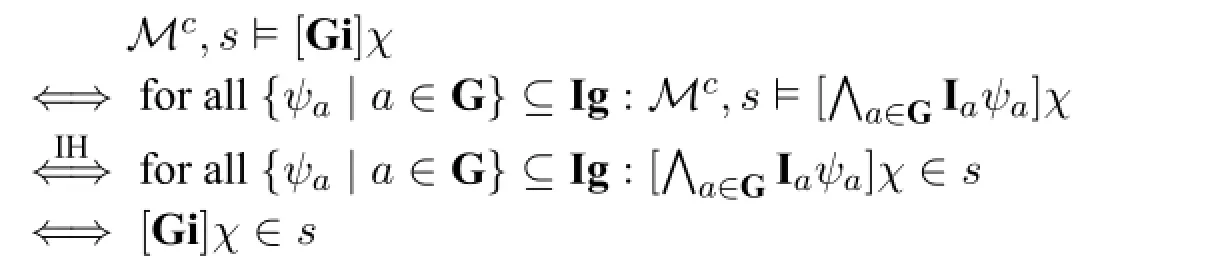
The last equivalence is due to Axiom GI and the fact thatsis closed under R(G)for the admissible form♯.□

Proposition 18(Completeness)GALI is complete with respect to the class of all frames.

ProofAssume thatφ/∈Thm,we want to show⊭φ.One may easily verify thatThmis a theory.By assumption,¬¬φ/∈Thm.Using Prop.15,we have thatThm+{¬φ}is a consistent theory containingThm∪{¬φ}.By Lindenbaum’s Lemma (Lem.1),there is as∈Scsuch that¬φ∈s,i.e.φ/∈s.Then applying to the truth lemma(Lem.2),we obtain thatMc,s⊭φ,thus⊭φ.□

7 Discussion and conclusion

In thispaper,we have proposed a group announcementlogic forignoranceGALI, which is an extension of the logic of ignorance with announcementsIgAand a group announcement operator for ignorance.We have established an expressive hierarchy forGALI,IgAand some related variations,on bothKandS5.In particular,we have shown that,GALIisnotatleastasexpressive asGALonK(Prop.6),andGALisnotat least as expressive asGALIonS5 in multi-agent setting(Prop.9).This implies thatGALandGALIare incomparable onKin multi-agent setting(Coro.2).We have given the frame undefinability results for our logicGALI.We have presented a complete infinitary axiomatization forGALI,with some revisions of the method in the literature.We can also investigate various extensions on special frame classes for this logic(see[15,Sec.5]).

As for future research,we hope to find a finitary axiomatization forGALI(similar to open questions forAPAL,GALandAIgA),and show the Conjectures 1 and 2,thereby completing the expressive hierarchy of the various languages aforementioned.Besides,as we have shown in Props.1 and 2,our[Gi]operator has many distinct properties from itsGALcounterpart[G],thus we can also explore other properties of the new operator.For example,does it satisfy the Church-Rosser property,that is,is〈Gi〉[Gi]φ→[Gi]〈Gi〉φvalid for allφ∈GALI?How about its generalized version〈Gi〉[Hi]φ→[Hi]〈Gi〉φ?And what about their converses [Gi]〈Gi〉φ→〈Gi〉[Gi]φand[Hi]〈Gi〉φ→〈Gi〉[Hi]φ?As far as we know,one such variation[Gi]〈Gi〉φ→〈Gi〉[Gi]φis invalid(in comparison with the fact that it is unknown whether[G]〈G〉φ→〈G〉[G]φis valid or not[1,p.68]),as illustrated with a simple modelMthat have only one worlds:in this model,all formulas of the formIaφare false,so[Gi]〈Gi〉φ→〈Gi〉[Gi]φisnotvalid ifG={a},and therefore neither is its generalized version[Hi]〈Gi〉φ→〈Gi〉[Hi]φ.Besides,we conjecture that the model checking problem forGALIis PSPACE-complete;that is,this decision problem is in PSAPCE and also PSAPCE-hard.We also leave it for future work.

[1]T.Ågotnes,P.Balbiani,H.van Ditmarsch and P.Seban,2010,“Group announcement logic”,Journal of Applied Logic,8:62–81.

[2]M.Aloni,P.Égré and T.Jager,2013,“Knowing whether A or B”,Synthese,190(14): 2595–2621.

[3]M.Attamah,H.van Ditmarsch,D.Grossiand W.van der Hoek,2014,“Knowledge and gossip”,Proceedings of 21st European Conference on Artificial Intelligence,Springer.

[4]J.Baier,B.Mombourquette and S.McIlraith,2014,“Diagnostic problem solving via planning with ontic and epistemic goals”,Proceedings of the Fourteenth International Conference Principles of Knowledge Representation and Reasoning,pp.388–397.

[5]P.Balbiani,2015,“Putting right the wording and the proof of the truth lemma for APAL”,Journal of Applied Non-Classical Logics,25(1):2–19.

[6]P.Balbiani and H.van Ditmarsch,2015,“A simple proof for the completeness of APAL”,Studies in Logic,8(1):65–78.

[7]P.Balbiani,A.Baltag et al.,2007,“What can we achieve by arbitrary announcements? A dynamic take on Fitch’s knowability”,in D.Samet(ed.),Proceedings of TARK XI, pp.42–51,Presses Universitaires de Louvain.

[8]P.Balbiani,A.Baltag et al.,2008,“‘Knowable’as‘known after an announcement’”,Review of Symbolic Logic,1(3):305–334.

[9]P.Blackburn,M.de Rijke and Y.Venema,2001,Modal Logic,Cambridge:Cambridge University Press.

[10]S.Bromberger,1992,On What We Know We Don’t Know:Explanation,Theory,Linguistics,and How Questions Shape Them,Chicago:The University of Chicago Press.

[11]I.Ciardelli,2014,“Modalities in the realm of questions:Axiomatizing inquisitive epistemic logic”,Advances in Modal Logic,Vol.10,pp.94–113,College Publications.

[12]I.Ciardelliand F.Roelofsen,2011,“Inquisitive logic”,JournalofPhilosophicalLogic,40(1):55–94.

[13]I.Ciardelli and F.Roelofsen,2015,“Inquisitive dynamic epistemic logic”,Synthese,192(6):1643–1687.

[14]M.Cresswell,1988,“Necessity and contingency”,Studia Logica,47:145–149.

[15]H.van Ditmarsch and J.Fan,2016,“Propositional quantification in logics of contingency”,Journal of Applied Non-Classical Logics,26(1):81–102.

[16]H.van Ditmarsch,W.van der Hoek and B.Kooi,2007,Dynamic Epistemic Logic, Berlin:Springer.

[17]H.van Ditmarsch,J.Fan etal.,2014,“Some exponentiallowerbounds on formula-size in modal logic”,Advances in Modal Logic,Vol.10,pp.139–157.

[18]J.Driver,1989,“Virtues of ignorance”,The Journal of Philosophy,86:373–384.

[19]J.Driver,2001,Uneasy Virtue,Cambridge:Cambridge University Press.

[20]J.Fan and H.van Ditmarsch,2015,“Neighborhood contingency logic”,in M.Banerjee and S.Krishna(eds.),Proceedings of the Sixth Indian Conference on Logic and Its Applications,LNCS,Vol.8923,pp.88–99,Springer.

[21]J.Fan,Y.Wang and H.van Ditmarsch,2014,“Almost necessary”,Advances in Modal Logic,Vol.10,pp.178–196.

[22]J.Fan,Y.Wang and H.van Ditmarsch,2015,“Contingency and knowing whether”,The Review of Symbolic Logic,8(1):75–107.

[23]S.Firestein,2012,Ignorance:How It Drives Science,New York:Oxford University Press.

[24]O.Flanagan,1990,“Virtue and ignorance”,The Journal of Philosophy,87(8):420–428.

[25]T.French and H.van Ditmarsch,2008,“Undecidability for arbitrary public announcement logic”,in C.Areces and R.Goldblatt(eds.),Advances in Modal LogicVol.7, Proceedings of the seventh conference“Advances in Modal Logic”,pp.23–42,College Publications.

[26]R.Goldblatt,1982,AxiomatisingtheLogicofComputerProgramming,Springer-Verlag.

[27]A.Goldman and E.Olsson,2009,“Reliabilism and the value of knowledge”,in A. Haddock,A.Millar and D.Pritchard(eds.),Epistemic Value,pp.19–41,Oxford:Oxford University Press.

[28]N.Gulley,1968,The Philosophy of Socrates,New York:St.Martin’s Press.

[29]S.Hart,A.Heifetz and D.Samet,1996,“Knowing whether,knowing that,and the cardinality of state spaces”,Journal of Economic Theory,70(1):249–256.

[30]S.Hedetniemi,S.Hedetniemi and A.Liestman,1988,“A survey of gossiping and broadcasting in communication networks”,Networks,18:319–349.

[31]A.Heifetz and D.Samet,1993,Universal Partition Structures,Tel Aviv University.

[32]J.Hintikka,1962,Knowledge and Belief,Ithaca,NY:Cornell University Press.

[33]W.van der Hoek and A.Lomuscio,2003,“Ignore at your peril–Towards a logic for ignorance”,Proceedings of 2nd AAMAS,pp.1148–1149,ACM.

[34]W.van der Hoek and A.Lomuscio,2004,“A logic for ignorance”,Electronic Notes in Theoretical Computer Science,85(2):117–133.

[35]L.Humberstone,1995,“The logic ofnon-contingency”,NotreDameJournalofFormal Logic,36(2):214–229.

[36]K.Konolige,1982,“Circumscriptive ignorance”,AAAI-82:Proceedings of the Second AAAI Conference on Artificial Intelligence,pp.202–204,AAAI Press.

[37]S.Kuhn,1995,“Minimal non-contingency logic”,Notre Dame Journal of Formal Logic,36(2):230–234.

[38]L.B.Kuijer,2016,“Unsoundness of R([])”,Manuscript,available online at http: //personal.us.es/hvd/APAL_counterexample.pdf.

[39]B.G.Kyle,2015,“The new and old ignorance puzzles:How badly do we need closure?”,Synthese,192(5):1–31.

[40]J.McCarthy,1979,“First-order theories of individual concepts and propositions”,Machine Intelligence,9:129–147.

[41]T.Miller,C.Muise,P.Felli,A.R.Pearce and L.Sonenberg,2016,“‘Knowing whether’in proper epistemic knowledge bases”,AAAI-16:Proceedings of the 30th AAAI Conference on Artificial Intelligence,AAAI Press.

[42]H.Montgomery and R.Routley,1966,“Contingency and non-contingency bases for normal modal logics”,Logique et Analyse,9:318–328.

[43]P.L.Morvan,2010,“Knowledge,ignorance,and true belief”,Theoria,76:309–318.

[44]P.L.Morvan,2011,“On ignorance:A reply to Peels”,Philosophia,39(2):335–344.

[45]P.L.Morvan,2012,“On ignorance:A vindication of the standard view”,Philosophia,40(2):379–393.

[46]P.L.Morvan,2013,“Why the standard view of ignorance prevails”,Philosophia,41(1):239–256.

[47]Y.Moses,D.Dolev and J.Halpern,1986,“Cheating husbands and other stories:A case study in knowledge,action,and communication”,Distributed Computing,1(3): 167–176.

[48]E.J.Olsson and C.Proietti,2016,“Explicating ignorance and doubt:Apossible worlds approach”,in R.Peels and M.Blaauw(eds.),The Epistemic Dimensions of Ignorance, pp.81–95,Cambridge University Press.

[49]M.Pauly,2002,“A modal logic for coalitional power in games”,Journal of Logic and Computation,12(1):149–166.

[50]R.Peels,2010,“What is ignorance?”,Philosophia,38:57–67.

[51]R.Peels,2011,“Ignorance is lack of true belief:A rejoinder to Le Morvan”,Philosophia,39(2):344–355.

[52]R.Peels,2012,“The new view on ignorance undefeated”,Philosophia,40:741–750.

[53]R.Petrick and F.Bacchus,2004,“Extending the knowledge-based approach to planning with incomplete information and sensing”,Knowledge Representation and Reasoning,pp.613–622.

[54]J.Plaza,1989,“Logics of public communications”,Proceedings of the 4th ISMIS, pp.201–216,Oak Ridge National Laboratory.

[55]R.Reiter,2001,Knowledge in Action:Logical Foundations for Specifying and Implementing Dynamical Systems,Cambridge,MA:The MIT Press.

[56]R.B.Scherl and H.J.Levesque,1993,“The frame problem and knowledge-producing actions”,AAAI-93:Proceedings of the Eleventh National Conference on Artificial Intelligence,pp.689–695,AAAI Press.

[57]C.Steinsvold,2008,“A note on logics of ignorance and borders”,Notre Dame Journal of Formal Logic,49(4):385–392.

[58]P.Unger,1975,Ignorance:A Case for Skepticism,Oxford:Oxford University Press.

[59]G.Vlastos,1985,“‘Socrates’disavowal of knowledge”,The Philosophical Quarterly,35(138):1–31.

[60]Y.Wang,2016,“Beyond knowing that:A new generation of epistemic logics”,in H. van Ditmarsch and G.Sandu(eds.),Jaakko Hintikka on Knowledge and Game Theoretical Semantics,Springer.

[61]M.Zimmerman,2008,Living with Uncertainty:The Moral Significance of Ignorance, Cambridge:Cambridge University Press.

[62]E.Zolin,1999,“Completeness and definability in the logic of noncontingency”,Notre Dame Journal of Formal Logic,40(4):533–547.

宣告群组的无知来消除主体的无知——基于无知的一个群组宣告逻辑

范杰
北京师范大学哲学学院
fanjie@bnu.edu.cn

本文提出一个基于无知的群组宣告逻辑，该逻辑是带有宣告算子的无知逻辑加上一个基于无知的群组宣告算子的扩展，用以表达群组中的每个主体宣告他们各自的无知后什么东西为真。我们对比这一逻辑和文献中相关逻辑的相对表达力，并研究该逻辑的框架可定义性问题。另外，我们也提出一个公理化系统并证明它的完全性。

Received2016-06-15

*This research is funded by China Postdoctoral Science Foundation(2016M590061)and partly funded by National Social Science Key Project of China(15AZX020).We thank Louwe Kuijer for communicating an unsoundness proof to us(see footnote 4).We thank Hans van Ditmarsch and a reviewer of the journal for their insightful comments.