数学实验:让学生进入真学习
2017-01-19徐长凤
徐长凤
【摘要】曾几何时,数学实验进入了我们的视野,本学期,我校针对规律探究这类数学实验课开展了专门的研究。研究中发现,很多课堂上出现了走过场现象,本文以笔者执教的《和与积的奇偶性》为例,试述数学实验教学中,从问题的提出,实验设计,到实验开展、结论得出,都不忘记让学生进入一种真学习的状态中。
【关键词】数学实验 教学思考
《和与积的奇偶性》是苏教版数学五年级下册新增的内容,是一节综合实践课。课堂主要通过举例猜想验证,让学生来探究和与积的奇偶性规律。听过几节这样的课,很多因为课堂时间短,常常是通过几个例子发现规律,再举几个例子验证一下,便得出结论,虽然流畅,但常常给人一种蜻蜓点水、一带而过,感性有余、理性不足的感觉。
这也是一节数学实验课。因为数学实验不能仅局限于物化的实践操作,像这种内在的数式运算的规律研究过程也是一种特殊的数学实验。这样的课堂上,“怎么样在数学实验中避免匆匆走过场,让学习真正发生,把学生带入深度探究中”成了我在备课时主要思考的问题。
首先,我准备放慢脚步,将一课时改为两课时,第一课时,在老师指导下,让学生充分探究和的奇偶性,积累数学实验的活动经验;第二课时,由学生自主探究积的奇偶性,并交流分享;同时,蹲下身子,从读懂学生开始,课前用一个作业单对学生的现状做一深入了解,课堂以学生为师,让数学实验伴随着学生的奇思妙想展开,把学生的数学活动经验、数学思维带向更深处……
一、课前调查:让经验真唤醒
片段一:
师:请判断屏幕上出现的是奇数还是偶数?(12、9、215、30)
生:12、30是偶数,9、215是奇数。
师:怎么判断的?
生:个位是0、2、4、6、8的数是偶数,个位是1、3、5、7、9的数是奇数。
生:是2的倍数是偶数,不是2的倍数是奇数。
师:如果n是不为0的自然数,2n呢?
生:偶数。2的倍数是偶数。
师:这些学生画的呢?
生:偶数。
师:想想他们画出的奇数会是什么样的呢?大家判断一个数是奇数还是偶数,都有两种方法,既可以看个位,也可以看是否是2的倍数。
美国教育心理学家奥苏伯尔说过:“影响学生学习的最重要的原因是学生已经知道了什么,我们应当根据学生原有的知识状况进行教学。”
课前,我用一个作业单,了解了学生对数的奇偶性的已有经验。
调查中发现,全班学生对于判断一个数是奇数还是偶数,虽然知道两种方法,但都喜欢看表面,根据个位去判断,而不喜欢想实质,根据是否是“2的倍数”来判断。因此,开始的热身环节,我采用多种形式让学生判断,一方面,提高了学生兴趣,另一方面,唤醒了学生对奇数偶数的本质的理解。
二、课中实验:让学习真发生
1.实验方案引起学生自己讨论
片段二:
师:几个数的和到底是奇数还是偶数,和的奇偶性到底有什么规律呢?我们可以怎么研究呢?我们一起想想办法。
生:举例子。
师:举例是个不错的方法。那我们就从举例开始,你们准备先举几个数的和?
生:两个。
师:为什么?
生:最简单。
师:是,古人云,天下难事必做于易,遇上复杂的问题,我们可以从简单的入手开始研究。
师:怎么研究呢?出示:任意选两个数,算出他们的和,再看看和是奇数还是偶数。你有疑问吗?
生:有,不是任意选几组,这里选的应该有代表性,奇加奇,奇加偶,偶加偶。
师:对,学习数学应该严谨,你是说举例子要全面。如果有序看,两个数相加到底有几种呢,好像有四种:奇+奇,奇+偶,偶+偶,偶+奇。
生:“奇+偶,偶+奇”重复了,算同一种,学习过加法交换律了。
师:不错,有理有据,能主动把学过的知识运用起来,那我们至少举3个例子。
学生对举例、猜想、验证的方法并不陌生。因此,教师在这里放手让学生讨论实验方案,让学生真正参与进来。同时,在适当的时候加以点拨、评价,借用一句“天下难事必做于易” 既给了学生鼓励,同时,也让学生在经历自己讨论实验方案的过程中,体会到化复杂为简单的数学思想;对教材中“任意”二字的质疑,给学生积累了学习数学要严谨、举例既要全面又要有序的数学活动经验。从而,真学习在学生的真讨论中开始了。
2.实验过程引导学生全程参与
片段三:
探究实验活动
师:拿出探究表格,每人举三个例子,并算出和,看看有什么发现,再小组交流。
师生交流板书:奇+奇=偶,偶+偶=偶,奇+偶=奇
师:这些只是我们观察几个例子后发现的,只能算是猜想,到底对不对呢?还需要(生:验证)?怎么验证?(举例)
师:好的,每人再任意举个例子验证一下,再跟同桌具体说说符合不符合我们的猜想?
师:有不符合的反例吗?
生:有。我的奇数加奇数没有等于偶数。
师:太好了。我们都知道,反例只要找到一个,我们就能下结论。
师展示3+3=9。
生:噢,是我算错了。
这一环节,从让学生填写表格的方式举例,发现猜想,全班交流,到再举例,同桌验证,再到寻找反例,一波三折,初步让学生经历了举例、猜想、验证这一实验过程。特别是寻找反例的过程,让学生体会到“证伪”在数学学习中的价值。同时,也给了学生举例要细心、严谨的体验。
3.实验结果引发学生深度思考
片段四:
师:每个人举得都符合吗?
生:是。
师:能下结论了吗?
生:能。
师:能了呀,这样的例子举得完吗?
生:举不完。
师:虽然我们全班已经举了几百个例子,可是万一出现不符合的呢?再举一个,试试?还想再举吗?
生:不想,太多了。
师:怎么办?万一有一个不符合呢?还能有别的方法验证说明吗?
生:奇数和偶数个位的情况都只有五种,可以分别将个位的每种情况都列举出来。
师:只关注个位,确实可以大大减少列举的数量。应该是个可行的方法。师:同学们大多喜欢从数的角度去思考,还可以怎么思考呢,看下面一段话对你是否有启发,出示“形无数时难入微,数无形时少直观,数形结合百般好,数形分离万事休——华罗庚”。
生:噢,数形结合,画图。
师:前面看了很多同学画的图,能根据我们班孙峰和孔雨老师的提示,画个图表示偶数或奇数吗?
师展示:
师:能用画图的方法证明刚才的三个猜想一定是正确的吗?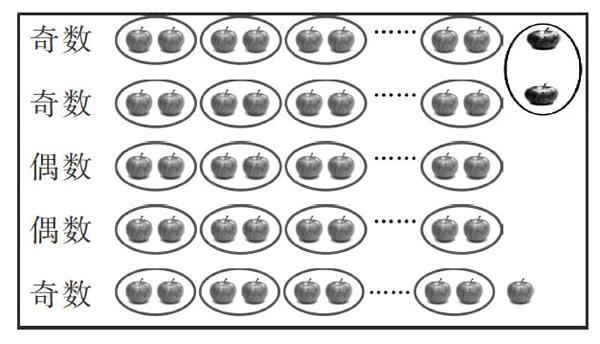
生:能。偶数加偶数,所有的苹果都成双,也就是一定是2的倍数。奇数加奇数也一样。
师:奇数加偶数呢?
生:一定是奇数。因为还会有一个苹果落单,也就不是2的倍数。
师:有了图,现在我们能下结论了吗?
生:能。
郞建胜老师说,追求本质,不厌其深。这里,老师首先让学生一再举例验证,学生最后都不想再举,可是,一个“万一”将学生带入知道要跳出举例,可又不知怎么办的“不愤不悱”状态,在眼看要得出结论的时候,不仅没有停下脚步,反而又让学生陷入深度思考。此时,抛出的华罗庚的数形结合思想给学生指明了方向,两个来自同伴中的小老师的话,给学生打开了又一扇窗。图形的出现,既形象直观,又让学生的猜想验证向前迈出了一大步,从关注现象到关注本质,用另一种形式说明,刚才举不完的例子不用再举,结论一定正确。更让学生体验到,严谨的数学思考带来的乐趣。
三、课尾拓展:让研究真开展
片段五:
师:接下来,你还想研究什么?
生:三个数、四个数和的奇偶性。
师:“奇+奇+…+奇+偶+偶+…+偶”这道式子的奇偶性你能研究吗?
生:用图就可以说明。偶数无论多少个出现都是成双成对的,奇数的个数也成双时,和就是偶数,奇数的个数落单时,和就是奇数。
师:厉害,你继续用刚才学到的方法来证明,虽然没画出来,根据你的回答,我们仿佛看到了你头脑中的图。
生:跟偶数的个数没关系,刚才已经证明偶数加偶数等于偶数,无论再加多少个偶数,都得偶数。只要看算式中奇数的个数就可以了,奇数个奇数,和是奇数,偶数个奇数,和为偶数。
师:同学们很棒,那么复杂的问题被你们变简单了,照这样说,几个数的和,只要数出其中奇数的个数就可以了。
师出示所编顺口溜:和的奇偶篇,只要一招鲜,奇数成了对,和是偶数吃遍天。
师:回顾今天的研究过程,我们从举例发现开始,猜想、举例、画图验证,最后得出了几个数的和的奇偶性结论。你还可以研究什么?
生:几个数的积的奇偶性。
师:带上这节课的研究经验,独立去研究,下节课分享。
……
生1:我从举例开始,从所举例子中,初步猜想奇×奇=奇,奇×偶=偶,偶×偶=偶。
画图后发现,奇×奇就是奇数个奇数相加,一定落单,积一定是奇数。同样,奇×偶和偶×偶都是偶数个数相加,积一定是偶数。
生2:我没有用画图,2n可以表示偶数,奇×偶,偶×偶,两个式子中都与2n相乘,一定是2的倍数。反之,奇×奇,结果不是2的倍数,一定是奇数。
课尾,简单的回顾,将本节数学实验课的活动经验留到了学生脑海中,在研究数学的过程中,做复杂想简单的数学思想,又一次给学生带来了数学的简洁美。更重要的是,这样的种子种到了孩子们的心中,他们在独立研究积的奇偶性时, 像模像样,不仅能根据举例、猜想、验证、再猜想、再证明的思路去展开研究,还自觉地用上了已知的结论或画图等多种方法来证明,让研究不再是走过场。
