解开函数及其图像的面纱
2017-01-19马爱平
马爱平
函数及其图像是初中数学的核心知识,是中考的重点内容,常考考点主要有:
考点1 直角坐标系与点的坐标特征
例1 (2016·甘肃)已知点P(0,m)在y轴的负半轴上,则点M(-m,-m+1)在( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限
【解析】因为点P(0,m)在y轴的负半轴上,所以m<0,所以-m>0,-m+1>0,所以点M在第一象限,故选择A.
【点评】解决这类问题要掌握点的横、纵坐标的取值与点所在象限(或坐标轴)的对应关系以及点的坐标特征.
考点2 确定函数自变量的取值范围
例2 (2016·四川内江)在函数y=[x-3x-4]中,自变量x的取值范围是( ).
A.x>3 B.x≥3
C.x>4 D.x≥3且x≠4
【解析】由题意,得x-3≥0且x-4≠0,∴x≥3且x≠4,故选择D.
【点评】求函数自变量的取值范围就是确定使函数解析式有意义的自变量的取值.此外,要注意“或”与“且”的区别.
考点3 用函数图像描述有关信息
例3 (2016·山东菏泽)小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度,图1是小明离家后他到学校剩下的路程S关于时间t的函数图像,那么符合上面行驶情况的图像大致是( ).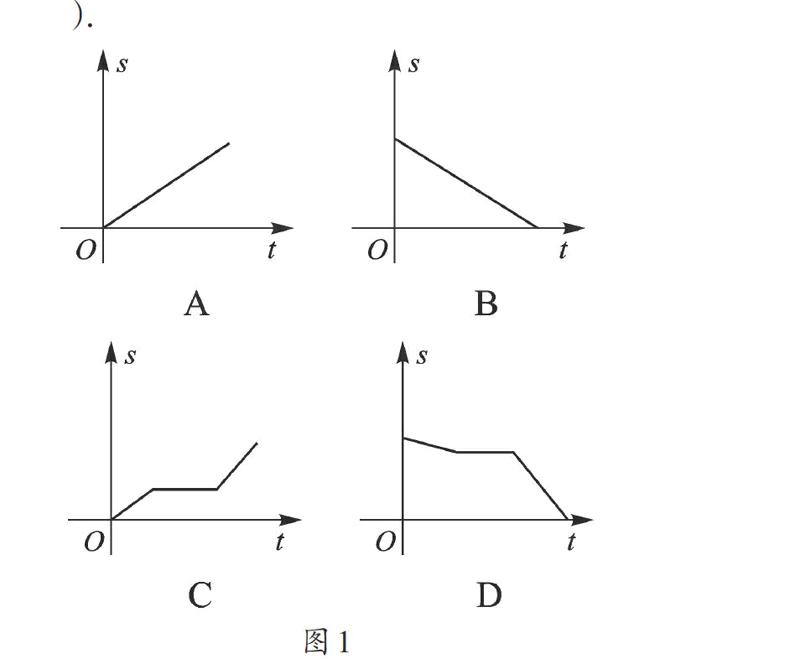
【解析】S是小明离家后到学校剩下的路程,即t=0时,S最大,到达学校时S=0,途中修车时间在变,而S不变,所以选D.
【点评】解答与日常生活相关的问题,要充分利用生活经验来帮助思考.
考点4 一次函数的图像及其性质
例4 (2016·广西玉林)关于直线l:y=kx+k(k≠0),下列说法不正确的是( ).
A.点(0,k)在l上
B.l经过定点(-1,0)
C.当k>0时,y随x的增大而增大
D.l经过第一、二、三象限
【解析】直接根据一次函数的图像与性质选择不正确的选项即可.当x=0时y=k,即点(0,k)在l上,故选项A正确;当x=-1时y=-k+k=0,故选项B正确;当k>0时y随x的增大而增大,故选项C正确;不能确定l经过第一、二、三象限,此选项错误.故选D.
【点评】本题主要考查了一次函数的性质,解题的关键是掌握一次函数的性质.
考点5 一次函数的应用
例5 (2016·吉林)甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙才出发.y甲、y乙与x之间的函数图像如图2所示.
(1)甲的速度是 km/h;
(2)当1≤x≤5时,求y乙关于x的函数解析式;
(3)当乙与A地相距240km时,甲与A地相距 km.
【解析】(1)根据图像得:360÷6=60(km/h);
(2)当1≤x≤5时,设y乙=kx+b,把(1,0)与(5,360)代入可解得k=90,b=-90,则y乙=90x-90;
(3)令y乙=240,得到x=[113],则甲与A地相距60×[113]=220(km).
【点评】本例(1)也可通过方程求解.(2)为(3)的求解做了铺垫,(3)是(2)的特殊情形,即求函数值是240时自变量的值.
考点6 反比例函数的图像及其性质
例5 (2016·黑龙江大庆)已知A(x1,y1)、B(x2,y2)、C(x3,y3)是反比例函数y=[2x]上的三点,若x1 A.x1·x2<0 B.x1·x3<0 C.x2·x3<0 D.x1+x2<0 【解析】∵反比例函数y=[2x]中,2>0,∴在每一象限内,y随x的增大而减小,∵x1 【点评】本题考查反比例函数图像上点的坐标特征,解题的关键是熟知反比例函数的增减性.本题是反比例函数性质的逆用,有一定的难度. 考点7 反比例函数的应用 例7 (2016·浙江湖州)湖州市菱湖镇某养鱼专业户准备挖一个面积为2000平方米的长方形鱼塘. (1)求鱼塘的长y(米)关于宽x(米)的函数表达式; (2)由于受场地的限制,鱼塘的宽最多只能挖20米,当鱼塘的宽是20米时,鱼塘的长为多少米? 【解析】(1)由长方形面积为2000平方米,得到xy=2000,即y=[2000x]; (2)当x=20(米)时,y=100(米),则当鱼塘的宽是20米时,鱼塘的长为100米. 【点评】反比例函数应用题一般难度不大,解题中要规范解题过程,不因容易而失分. 考点8 一次函数与反比例函数综合题 例8 (2016·四川广安)如图3,一次函数y1=kx+b(k≠0)和反比例函数y2=[mx](m≠0)的图像交于点A(-1,6)、B(a,-2). (1)求一次函数与反比例函数的解析式; 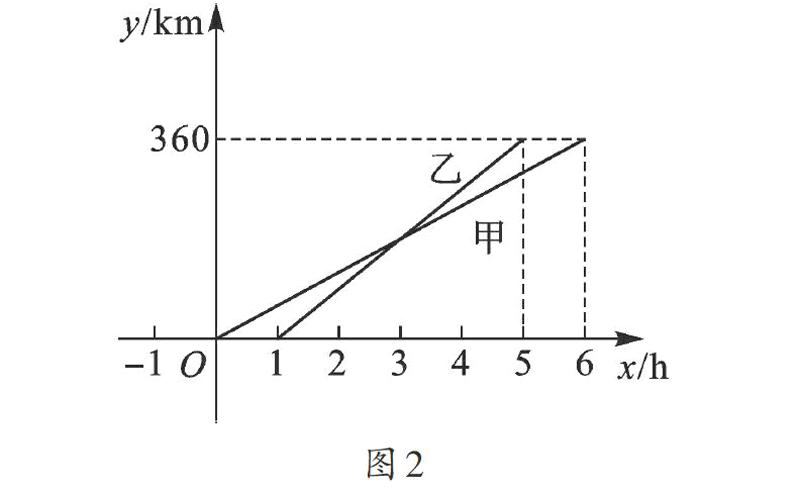
(2)根据图像直接写出y1>y2时x的取值范围.
【解析】(1)将A(-1,6)代入y2=[mx],得m=
-6.∴y2=[-6x].将B(a,-2)代入y2=[-6x],得a=3.∴B(3,-2).将A(-1,6)、B(3,-2)代入y1=kx+b,得[-k+b=6,3k+b=-2.]∴[k=-2,b=4.]∴y1=-2x+4.
(2)由图3可知,x<-1或0 【点评】求反比例函数解析式需要确定图像上一个点的坐标,求一次函数的解析式需要确定直线上两个点的坐标. 考点9 二次函数的图像及其性质 例9 (2016·广东广州)对于二次函数y=[-14]x2+x-4,下列说法正确的是( ). A.当x>0时,y随x的增大而增大 B.当x=2时,y有最大值-3 C.图像的顶点坐标为(-2,-7) D.图像与x轴有两个交点 【解析】将二次函数解析式配方得y=[-14] ·(x-2)2-3,其顶点坐标为(2,-3),选项C错误;∵a<0,∴抛物线开口向下,顶点为最高点,当x=2时,y有最大值-3,选项B正确;由抛物线开口向下,对称轴为x=2可知,当x>2时,y随x的增大而减小,选项A错误;一元二次方程[-14]x2+x-4=0中,Δ=-3<0,∴这个抛物线与x轴没有交点,选项D错误.故选B. 【点评】本题考查了二次函数的性质,根据抛物线解析式做出图像,答案便一目了然了. 考点10 二次函数、方程、不等式的应用题 例10 (2016·湖北襄阳)为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元,超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可卖出700盒,每盒售价每提高1元,每天要少卖出20盒. (1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式; (2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少? (3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒? 【解析】(1)y=700-20(x-45)=-20x+1600,(x≥45); (2)P=(x-40)(-20x+1600)=-20x2+2400x -64000=-20(x-60)2+8000.∵x≥45,a=-20<0,∴当x=60时,P有最大值,最大值为8000元.即当每盒售价定为60元时,每天销售的利润最大,最大利润为8000元; (3)由题意,得-20(x-60)2+8000=6000,解这个方程得x1=50,x2=70.∵抛物线P=-20(x-60)2+8000的开口向下,∴当50≤x≤70时,每天销售粽子的利润不低于6000元.又∵x≤58,∴50≤x≤58.∵在y=-20x+1600中,k=-20<0,∴y随x的增大而减小,∴x=58时,y有最小值。最小值y=-20×58+1600=440.即超市每天至少销售粽子440盒. 【点评】用好数量关系“利润=售价-进价”和“每天销售的利润=每盒的利润×每天的销量”是建立函数解析式的关键. 考点11 函数综合题 例11 (2016·山东泰安)如图4,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B. (1)求二次函数y=ax2+bx+c的表达式; (2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积; (3)若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标. 【解析】(1)设抛物线y=a(x-2)2+9,把A(0,5)代入得a=-1,∴y=-(x-2)2+9; (2)当y=0时,-(x-2)2+9=0,解得x1=-1,x2=5,∴E(-1,0),B(5,0),设直线AB的表达式为y=mx+n,把A(0,5),B(5,0)代入,得m=-1,n=5,∴y=-x+5.设P(x,-x2+4x+5),则D(x,-x+5),PD=-x2+4x+5+x-5=-x2+5x.∵AC平行于x轴,∴yA=yC=5,∴-x2+4x+5=5,得xC=4,∴AC=4,∴S四边形APCD=2(-x2+5x)=-2x2+10x,∵-2<0,∴当x=2.5时,四边形APCD的面积最大,最大面积为12.5; (3)过M作MH垂直于对称轴,垂足为H,∵MN∥AE,∴△HMN≌△OEA,∴HM=OE=1,NH=OA=5,∴M点的横坐标为x=1或3;当x=1时,M的纵坐标为8;当x=3时,M的纵坐标为8;N的纵坐标为3或13.∴M点的坐标为(1,8)时,N的坐标为(2,13)或M点的坐标为(3,8)时,N的坐标为(2,3). 【点评】二次函数的综合题涉及的知识点一般较多,有抛物线与坐标轴的交点坐标求法,几何图形的面积,三角形全等、相似,圆等,综合性较强,有一定难度.在解决有关平行四边形顶点问题时,通常应用平行四边形对边平行且相等,用平移法可找到相邻顶点间的联系.解题中常用到数形结合、分类及方程等思想方法. (作者单位:江苏省兴化市戴泽初级中学) 
