晶粒正常生长的Monte Carlo模拟
2017-01-19徐宗畅张耀予林一歆
王 岗,刘 艳,徐宗畅,肖 岗,张耀予,谭 凯,林一歆,
晶粒正常生长的Monte Carlo模拟
王 岗1,刘 艳1,徐宗畅1,肖 岗2,张耀予1,谭 凯2,林一歆1,2
1华中科技大学中欧清洁与可再生能源学院,武汉 4300742华中科技大学能源与动力工程学院,武汉 430074
本文建立了晶界能各向同性情况下晶粒生长的二维Monte Carlo模型,并对等温情况下的晶粒生长过程进行了模拟。在模拟过程中,对传统Monte Carlo方法中能量与概率统计方法进行了改进。为了更加直观地显示出晶粒生长过程中系统能量的变化,统计了在整个晶粒生长过程中能量的变化趋势,结果与晶粒尺寸变化相符合。模拟得到的晶粒生长指数在0.35 ~ 0.45之间,与理论值相符,证明了改进方法的可靠性。
计算机模拟;晶粒生长;Monte Carlo方法
Monte Carlo (MC) 方法是研究晶粒生长以及其相关过程的一种有效方法。使用MC方法研究晶粒生长的模型实际上是从Ising模型和Potts模型演化出来的,这两种方法最初被用于研究铁磁体系统。使用MC方法研究晶粒生长实际上就是将不同取向的晶体赋予不同的取向数,根据概率性原则来决定晶粒生长这一传播过程。
最早将MC方法运用到微观结构演化过程的人是Anderson等人[1]。后来,Anderson等人又将这种方法应用到晶粒生长[2]、含有杂质粒子时的晶粒生长[3],异常晶粒生长[4-6]等过程。随后,Q-state Potts模型开始被用于研究两相晶粒生长的机理[7,8]、晶粒生长过程中晶体结构的变化[9]以及外部条件对晶粒尺寸分布的影响[10]等。近年来,关于晶粒生长的MC模拟的研究主要着眼于对传统晶粒生长模型的修改以使其更加贴合实际的晶粒生长过程,例如:Mason等人[11]对模型中Hmiltonian函数以及转换概率进行了修改,模拟了动力学各向异性晶粒生长;Fang等人[12]运用新的模拟算法模拟了单相和两相陶瓷材料在烧结过程中材料组织结构的演化;Wang等人[13]通过改进的MC算法模拟了晶体的初次再结晶过程和退火孪晶现象;Allen等人[14]运用统计学方法,量化晶粒各向异性的程度,然后通过MC方法模拟了单相材料的各向异性生长。
国内学者对晶粒生长MC模拟的研究也取得了一些显著的进展。秦湘阁等人[15]运用MC方法对单相多晶体各向同性颗粒组织进行了三维建模并模拟其生长过程;钟晓征等人[16,17]运用MC方法模拟了多晶材料晶粒生长,并模拟了正常晶粒生长和异常晶粒生长两种情况;张继祥等人[18]提出了一种“择优转换”方法对MC方法进行了改进,模拟了晶粒的生长过程;王海东等人[19]根据晶粒生长机理建立改进的转换概率模型模拟焙烧过程中的晶粒生长,并对不同温度,不同焙烧时间以及不同激活能条件下的晶粒生长过程进行了模拟;王浩等人[20]运用MC方法对3种现存的三维个体晶粒生长速率拓扑依赖性方程进行了仿真验证;马非等人[21]采用改进的MC模拟方法对不同烧结温度和保温时间下的晶粒生长演化过程进行计算机模拟,并使用多孔Al2O3陶瓷烧结实验过程中的晶粒生长数据对模型进行了验证。
在实际应用中,传统的MC方法存在效率低下的问题,这是因为在传统MC方法中,格点取向改变范围是在1 ~之间取一随机数作为转变取向。在实际的晶粒生长过程中,晶粒生长实际上只受其相邻格点影响,其余格点对其取向转变影响微乎其微。如果将所有格点取向都考虑进去,难免会造成计算效率低下的情况。因而,本文根据实际情况对晶粒取向转变的算法进行了改进,在格点重新定向时,不再考虑所有的取向值,而仅考虑其邻近格点的取向值,这样就大大缩减了计算时间,提高了计算的准确率。
1生长动力学
1952年,Burke发现晶粒的平均尺寸与晶粒生长时间之间存在一定的关系:

(1)
式中,1是一个与温度和晶界移动率有关的常数,0是系统在初始时刻的平均晶粒尺寸,是晶粒生长指数。关于晶粒生长指数的取值历来都有争议,因为在不同实验条件、不同模型条件下模拟出的结果都不相同,一般而言,在不考虑二相粒子以及晶粒纯度对于晶粒生长的影响的条件下,值一般趋近于2。
晶粒生长速率与晶粒尺寸之间的关系是由Hillert[22]提出的,其关系式如下:

(2)
其中,是一个与晶界迁移率和晶界能有关的常数,是单个晶粒的半径,cr是临界半径。
晶界全都是高能量区域,晶界的存在会增加系统的自由能,从而使系统处于一种亚稳定的状态[23]。当外界提供一定的能量波动 (例如退火过程),系统中的晶界就会通过自身调节,使晶界处于新的(亚) 稳定状态,从而降低整个系统的能量。
按具体形貌讨论总的晶界能可以更简单地讨论每一个晶界对结合点的作用力,从而获得晶界结合点的平衡条件。如图1所示,晶界结合点的平衡条件可以表示为:
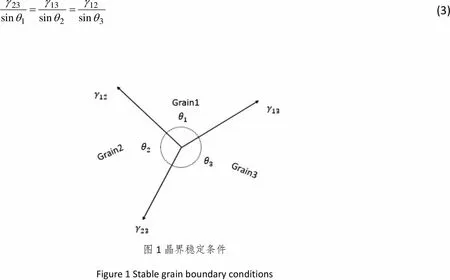
(3) 图1晶界稳定条件Figure 1 Stable grain boundary conditions
晶界张力在三叉点处的平衡使晶界发生弯曲。在弯曲界面上存在一个指向界面曲率中心的力,作用在单位面积上的力用表示,在这里称为晶界移动驱动力,大小由Laplace's方程给出:

(4)
其中,1和2为晶界的两个主曲率半径,为界面张力。在二维系统中,2®¥,故上式可简化为:

(5)
设在驱动力作用下,晶界移动一段距离,则能量变化D为

(6)
其中为晶界迁移方向与方向的夹角。
假设系统中界面张力为常数,由于驱动力的作用,晶粒长大过程中晶界将始终朝其曲率中心方向移动,所以具有内凹型晶界的晶粒将长大,晶界外凸的晶粒将缩小,而平直晶界因其曲率半径无限大,驱动力等于零,将静止不动。
图2所示为一系列等边长的边型晶粒。由图2可见,大于六边的结构具有内凹边界,他们在退火过程中会不断长大;而小于六边的为外凸晶界,在退火过程中不断减小。这就是所谓的-6规则。Mullins[24]指出晶体面积的变化率与其拓扑关系存在如下的线性关系:

(7)
其中是指定晶粒的边界数,是一个与晶界迁移率和晶界能成比例的常数。式 (7) 表明,当晶粒边界数大于6时,晶粒长大;相反,当小于6时,晶粒将收缩;当边界数等于6时,晶粒将不生长。
图2晶粒拓扑结构
Figure 2 Grain topological structures
2模拟方法
MC-Potts模型是一种离散的统计方法。因为它十分适用于多相系统 (例如固相与液相),所以它被广泛应用于扩散、离子传输、相变等现象的模拟研究。
利用Potts模型模拟晶粒生长时,首先应把晶粒形貌离散化,如图3所示[25]。每一个离散格点都被赋予1 ~之间的数值,这个数值对应于晶粒在微观下的取向。研究表明,的取值应当大于32[25],因为只有这样才能减少取向数对于模拟结果的影响。
Figure 3 Discrete structure
晶界的能量由不同格点之间的相互作用给出,用Hmiltonian方程来描述:
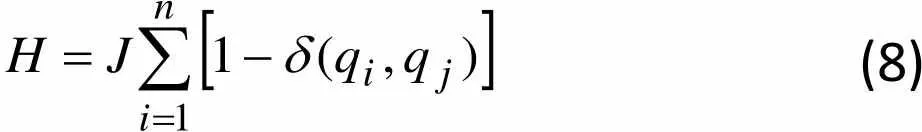
(8)
式中,是克罗内克符号,是相邻格点之间的作用力,是周围格点总数 (本文我们取如图3所示点阵,因此任意一个格点周围有8个邻接格点),q表示选定格点取向,q表示相邻格点的取向。
在MC-Potts模型模拟晶粒生长的过程中,我们首先随机选取一个格点,计算该格点取向与相邻格点是否发生转变,转变概率由式 (9) 给出:

(9)
其中,D表示取向改变过程中能量的变化,由式 (10c) 计算得出,是玻尔兹曼常数,是绝对温度。
在传统的MC方法中,能量变化是这样计算的:首先随机选取一个格点,已知这个格点的取向值为,那么,我们就在除了以外的1 ~个取向中随机选取一个取向,根据下列公式计算出该格点取向变为相邻取向后,系统能量差值的变化D,进而求出其转换概率:

(10a) (10b) (10c)
但是在实际的晶粒生长过程中,我们所选取的格点生长方向实际上只与其相邻晶粒有关。传统MC方法将所有的晶粒取向作为格点可能将要转变的方向显然是不合适的。在本文中,对于所选取的格点,其转变取向必然要在其相邻8个格点中选取。为了更符合实际情况,我们将这8个格点的取向都加以考虑,分别计算出取向转变后的能量改变 (D1~D8),比较这8个能量差值的大小,选取绝对值最大的D(即取向转变后系统能量损失最大) 对应的取向作为转变取向,再根据式 (9) 求出其转换概率。
3 模拟流程
对晶粒生长的Monte Carlo模拟流程如下 (图4):
(1) 输入模拟初始数据 (取向数、格点数、模拟步数MCS等);
(2) 建立晶粒初始形貌,将其离散到格点上;
(3) 对每一个格点随机赋予取向数,代表该格点处的晶粒取向;
(4) 随机选取一个格点,根据式 (8) 计算格点能量;
(5) 计算该格点取向转变为相邻取向后的能量;
(6) 计算结点取向数改变前后能量差Δ;
(7) 根据式 (9) 计算转换概率;
(8) 在模拟过程中产生[0,1] 之间的随机数,比较和,判断取向改变是否被接受:w³时接受;<时不接受。
(9) 如果取向改变被接受,则该格点取向数改变为其相邻格点,晶粒长大;反之,如果改变未被接受,该晶粒则没有长大;
(10) 一个MCS步完成;
(11) 再重新选取一个格点,按照(4) ~ (9) 的步骤模拟,直至完成所有循环。
按照上述模拟流程使用Matlab软件编写了软件,并对模拟结果进行了后处理。模拟采用的点阵为100´100,取向值设定为32,模拟步数MCS为1000。
Figure 4 Flow diagram of the simulation process
4模拟结果与分析
图5所示为模拟建立的晶粒初始形貌,图6则给出了晶粒生长过程中晶粒形貌随时间的演化情况。可以看出,在= 0 MCS ~ 250 MCS之间,晶粒生长迅速,尺寸变化明显,大晶粒吞并小晶粒,晶界交点处多为120度,证明该模拟很好地符合了实验现象。而在250 MCS后,晶粒尺寸变化并不明显,于是我们统计了晶粒平均尺寸等参数来进行比较分析。
图5晶粒初始形貌 (= 0)
Figure 5 The initial grain morphology (= 0)
晶粒平均尺寸的变化规律如图7所示。可以看出,晶粒快速生长发生在0 MCS ~ 200 MCS这个阶段;进入400 MCS后,晶粒尺寸基本保持稳定。
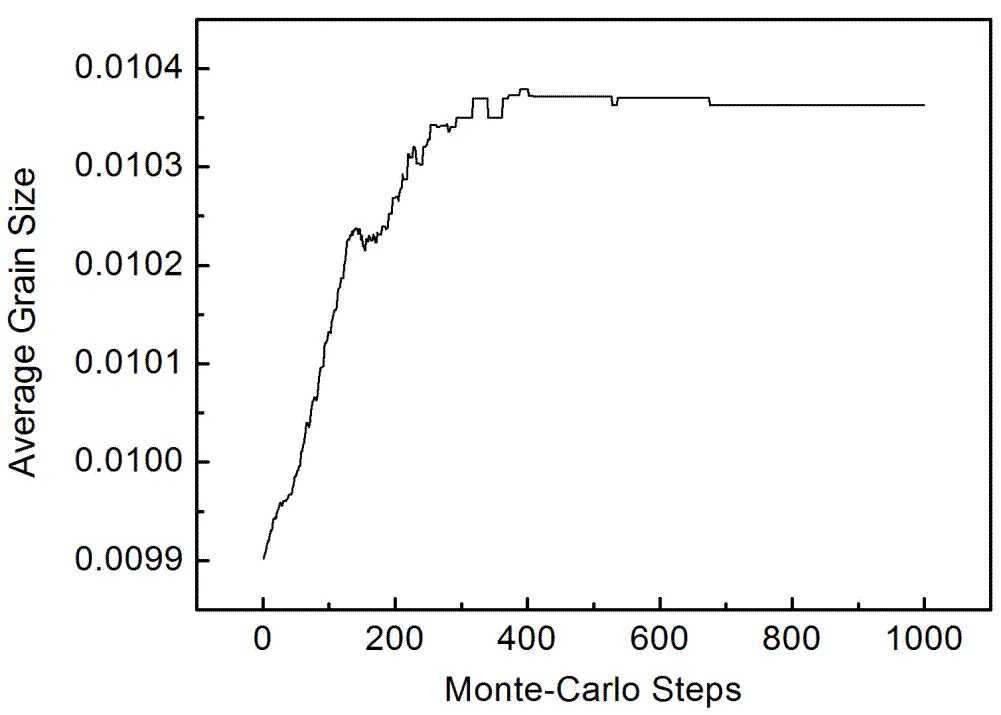
图7晶粒平均尺寸随模拟时间的变化
Figure 7 Variation of average grain size with simulation time
为了进一步研究晶粒生长过程,我们统计了每一个MCS步时整个晶粒所储存的能量,以便清楚地显示出晶粒长大过程中整个系统的能量变化,结果如图8所示。可以看出,晶粒生长过程实际上就是晶粒晶界储能减少的过程,随着晶粒储能的减少,晶粒生长。在0 MCS ~ 200 MCS之间储能急剧下降,对应于图7中晶粒尺寸的急剧上升;400 MCS后,晶粒尺寸保持稳定,晶粒储能基本不变。
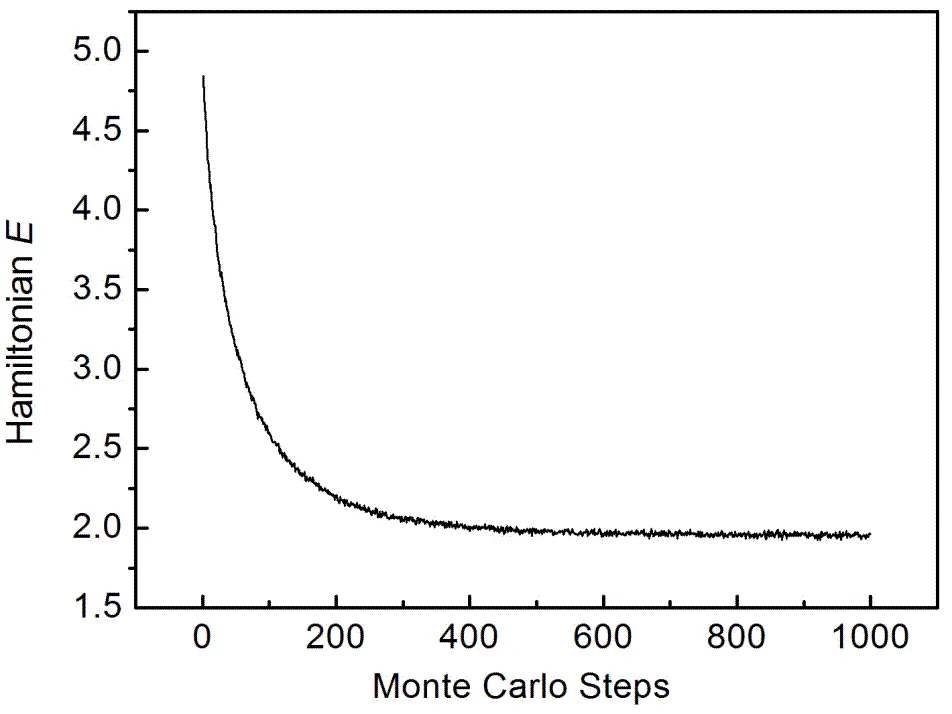
图8 系统总能量随模拟时间的改变
Figure 8 Variation of total system energy with simulation time
根据模拟结果,我们可以得到晶粒生长曲线如图9所示:晶粒生长指数在0 MCS ~ 200 MCS之间有一个较大的变化,但最后稳定在0.35 ~ 0.45之间,这与理论值0.5差别不大。研究表明,理论值0.5只是针对理想状况,实际上由于杂质、间隙等因素的影响,大部分材料晶粒生长指数应当在0.1 ~ 0.4之间,这与我们的模拟结果相符。
图9晶粒生长指数随时间的变化
Figure 9 Variation of grain growth exponent with simulation time
5结论
本文根据传统晶粒生长的Monte Carlo模型,提出了格点重新取向过程中新的随机提取方法。模拟分析证明了该改进算法的可靠性。将晶粒平均尺寸与系统能量相比较,验证了晶粒长大过程对应于系统能量减少这一现象。模拟得到的晶粒生长指数在0.35 ~ 0.45之间,与使用传统Monte Carlo方法模拟得到的结果 (= 1/3[26]) 相比,更加贴近于理论结果。
[1] ANDERSON MP, SROLOVITZ DJ, GREST GS, et al. Computer simulation of grain growth: I, kinetics [J]. Acta Metallurgica, 1984, 32 (5): 783-791.
[2] SROLOVITZ DJ, ANDERSON MP, SAHNI PS, et al. Computer simulation of grain growth: II, grain size distribution, topology, and local dynamics [J]. Acta Metallurgica, 1984, 32 (5): 793-802.
[3] SROLOVITZ DJ, ANDERSON MP, GREST GS, et al. Computer simulation of grain growth: III, influence of a particle dispersion [J]. Acta Metallurgica, 1984, 32 (9): 1429-1438.
[4] SROLOVITZ DJ, GREST GS, ANDERSON MP. Computer simulation of grain growth: V, abnormal grain growth [J]. Acta Metallurgica, 1985, 33 (12): 2233-2247.
[5] ROLLETT AD, SROLOVITZ DJ, ANDERSON MP. Simulation and theory of abnormal grain growth: isotropic grain boundary energies and mobilities [J]. Acta Metallurgica, 1989, 37 (4): 1227-1240.
[6] ROLLETT AD, MULLINS WW. On the growth of abnormal grains [J]. Scripta mETALLURGICA ET mATERIALIA, 1996, 36 (9): 975-980.
[7] OKUDA K and rollett AD. Monte Carlo simulation of elongated recrystallized grains in steels [J]. Computational Materials Science, 2005, 34 (3): 264-273.
[8] COUTURIER G, DOHERTY R, MAURICE C, et al. 3D finite element simulation of the inhibition of normal grain growth by particles [J]. Acta Materialia, 2005, 53 (4): 977-989.
[9] IVASISHIN OM, SHEVCHENKO SV, VASILIEV NL, et al. 3D Monte-Carlo simulation of texture- controlled grain growth [J]. Acta Materialia, 2003, 51 (4): 1019-1034.
[10] ZOLLNER D, STREITENBERGER P, RIOS PR. Shedding some light on the early grain growth regime: about the effect of the initial microstructure on normal grain growth [J]. Computational Materials Science, 2016, 113: 11-20.
[11] MASON JK, LIND J, LI SF, et al. Kinetics and anisotropy of the Monte Carlo model of grain growth [J]. Acta Materialia, 2015, 82: 155-166.
[12] FANG B, HUANG C, XU C, et al. Numerical simulation of microstructural evolution of ceramic tool materials [J]. Computational Materials Science, 2008, 44 (2): 707-715.
[13] WANG W, HELBERY AL, BRISSET F, et al. Monte Carlo simulation of primary recrystallization and annealing twinning [J]. Acta Materialia, 2014, 81: 457-468.
[14] ALLEN JB, CORNWELL CF, DEVINE BD, et al. Simulations of anisotropic grain growth in single phase materials using Q-state Monte Carlo [J]. Computational Materials Science, 2013, 71: 25-32.
[15] 秦湘阁, 刘国权. 多晶体晶粒尺度三维组织建模及可视化[J]. 北京科技大学学报, 2001, 23 (6): 519-522.
[16] 钟晓征, 陈伟元, 王豪才, 等. 多晶材料晶粒生长的Monte Carlo计算机模拟方法:Ⅰ, 模拟正常晶粒生长[J]. 功能材料, 1999, 17 (3): 9-12.
[17] 钟晓征, 陈伟元, 王豪才, 等. 多晶材料晶粒生长的Monte Carlo计算机模拟方法:Ⅱ,模拟异常晶粒生长[J]. 功能材料, 999, 17 (3): 13-15.
[18] 张继祥, 关小军, 孙胜. 一种改进的晶粒长大Monte Carlo模拟方法[J]. 金属学报, 2004, (5): 457-461.
[19] 王海东, 张海, 李海亮, 等. 焙烧过程晶粒生长的Monte Carlo模拟[J]. 中国有色金属学报, 2007, 17 (6): 990-996.
[20] 王浩, 刘国权, 秦湘阁. 三维晶粒长大速率方程的大尺度Potts模型Monte Carlo仿真验证[J]. 金属学报, 2008, 44 (1): 13-18.
[21] 马非, 申倩倩, 贾虎生, 等. 用改进的Monte Carlo算法模拟多孔Al2O3陶瓷烧结过程中的晶粒生长[J].人工晶体学报, 2011, (5): 1299-1304.
[22] HILLERT M. On the theory of normal and abnormal grain growth [J]. Acta Metallurgica, 1965, 13 (3): 227-238.
[23] 毛卫民, 赵新兵. 金属的再结晶与晶粒长大[M]. 北京: 冶金工业出版社, 1994.
[24] MULLINS WW. Two-dimensional motion of idealized grain boundaries [J]. Journal of Applied Physics, 1956, 27 (8): 900-904.
[25] ZHANG D, WENG G, GONG S, et al. Computer simulation of grain growth of intermediate- and final-stage sintering and Ostwald ripening of BaTiO3-based PTCR ceramics [J]. Materials Science and Engineering B, 2003, 99 (1): 428-432.
[26] 叶日晴, 赵建华, 何陵辉. 退火过程中晶粒生长的二维计算机模拟[J]. 无机材料学报, 2001, (1): 122-128.
Monte Carlo Method for Normal Grain Growth Similation
WANG Gang1, LIU Yan1, XU Zong-Chang1, XIAO Gang2, ZHANG Yao-Yu1, TAN Kai2, LIN Yi-Xin1,2
1China-EU Institute for Clean and Renewable Energy, Huazhong University of Science&Technology, Wuhan 430074, China2School of Energy and Power Engineering, Huazhong University of Science&Technology, Wuhan 430074, China
A two-dimensional Monte Carlo model for the grain growth in under the isotropic condition was established and used to simulate the normal grain growth process. In the simulation process, some changes in the part of energy calculation and probability statistics in the traditional Monte Carlo method were made. The simulation results confirmed that the energy evolution of the system is corresponding to the grain size change. The obtained grain growth exponent,= 0.35 ~ 0.45, is close to its theoretic value, proving the reliability of the improved method.
Computer simulation; Grain growth; Monte Carlo method
TB34
1005-1198 (2016) 06-0434-08
A
10.16253/j.cnki.37-1226/tq.2016.07.002
2016-06-20
2016-10-31
国家自然科学基金 (21203069)。
王 岗 (1991-), 男, 河南汤阴人, 硕士研究生。E-mail: wanggangty44@gmail.com。
林一歆 (1982-), 女, 湖北武汉人, 副教授。E-mail: yixinlin@hust.edu.cn。
