波形钢腹板组合曲线箱梁横隔板间距研究

田宝升，丁汉山

（东南大学，江苏 南京 210096）

波形钢腹板组合曲线箱梁横隔板间距研究

田宝升，丁汉山

（东南大学，江苏 南京 210096）

波形钢腹板组合曲线箱梁腹板具有手风琴效应，纵向弹性模量很小，相比混凝土腹板箱梁，容易发生畸变变形，因此需要设置一定数量的横隔板减小截面畸变的影响。文章采用有限元Ansys模拟分析曲线箱梁高宽比、曲率半径对横隔板间距的影响，按截面翘曲正应力与弯曲正应力之比≤10%的原则，拟合出横隔板合理间距计算公式，对实际工程应用具有一定的参考价值。

波形钢腹板；曲线箱梁；横隔板；翘曲正应力

波纹钢腹板组合曲线箱梁是近年发展起来的一种旨在降低自重、增大预应力效率的新桥型，该桥型相比混凝土箱梁桥自重降低，甚至达到20%［1-2］，而且避免了混凝土腹板易开裂的现象。

波纹钢腹板由于其手风琴效应，纵向弹性模量很小，在相同的扭转荷载作用下，相比混凝土腹板箱梁，截面更容易发生畸变变形和纵向翘曲变形，同时产生不可忽略的横向弯曲正应力和畸变翘曲正应力［3-4］。横隔板不仅可以有效限制截面畸变变形，而且可以提高箱梁的抗扭刚度，有利于荷载横向分布及应力的均布分布［5］。

然而横隔板的设置不仅会增加施工难度，还会增大箱梁自重，因此国内外很多学者对箱梁横隔板的合理设置进行了系统研究，如李宏江［6］针对波纹钢腹板直线箱梁，研究了跨高比对横隔板间距的影响，提出横隔板合理间距估算公式；Park N［7］针对不同畸变翘曲应力与弯曲应力比例，研究了圆心角、高宽比、跨度和跨数对平钢-混组合曲线箱梁横隔板设置间距的影响，绘制了相应的合理横隔板间距图表。

本文基于有限元Ansys模拟，通过应力分解计算曲线箱梁翘曲正应力与弯曲正应力的比例，分析箱梁高宽比H/B、曲率半径R对波形钢腹板曲线箱梁的横隔板间距影响，提出横隔板合理间距估算公式，为实际工程提供一定的参考。

1 板壳单元的应力分解

采用Ansys板壳单元分析曲线箱梁应力时，在结果中只能提取节点的总应力，而曲线箱梁由于弯扭耦合，总应力包括弯曲应力和翘曲应力。如图1所示，底板与腹板交界处内、外侧（以下简称内、外侧）总正应力σin、σout，为了将耦合的应力进行分离，笔者不考虑曲率半径对剪力滞系数λ的影响，即内外侧弯曲应力大小相等σMin=σMout=λσM，弯矩产生的弯曲应力λσM沿截面呈对称分布；扭转产生的翘曲正应力σωT（包括扭转正应力σω和畸变正应力σD） 沿截面反对称分布。因此底板内、外侧总应力σin、σout可用弯曲正应力λσM、翘曲正应力σωT表示，见式（1）。

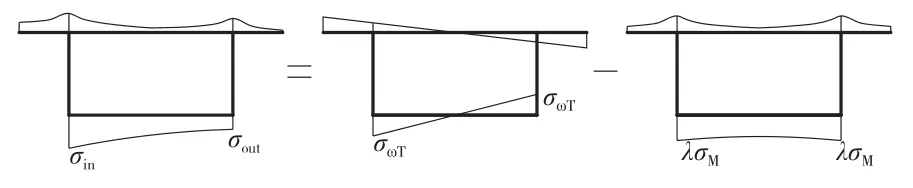
图1 底板应力分解示意图

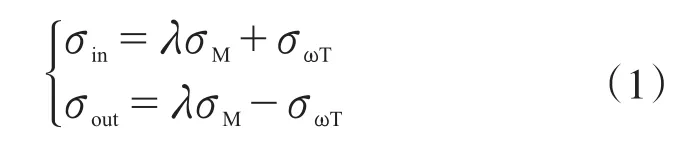
底板的耦合的弯曲正应力λσM、扭转翘曲正应力σωT也可用内、外侧总应力σin、σout来表示：

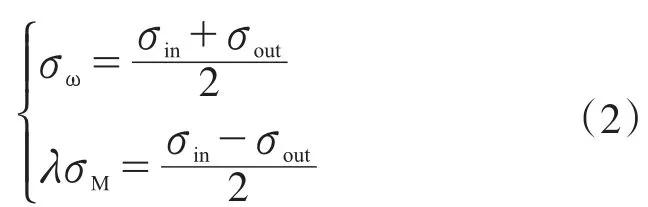
对于顶板有限元应力结果，弯扭应力分解方法同样适用；对于波纹钢腹板，由于纵向弹模很小可忽略不计，因而腹板所承受的弯曲正应力和翘曲正应力均为0。

2 有限元模型

为了研究横隔板对波纹钢腹板翘曲正应力变化的影响，采用有限元Ansys模拟， 模型尺寸如图2所示，跨径51.6 m，曲率半径R=200 m，高跨比为1/17，圆心角15°，波纹钢腹板采用1200型，尺寸如图3所示。

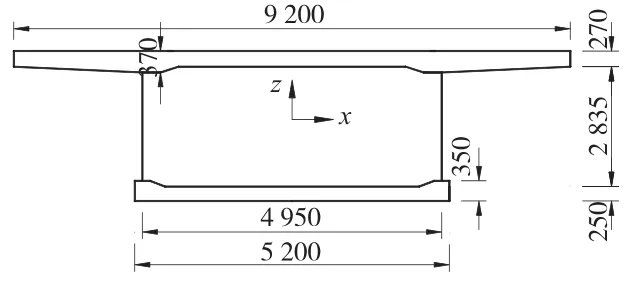
图2 跨中截面几何尺寸（单位：mm）

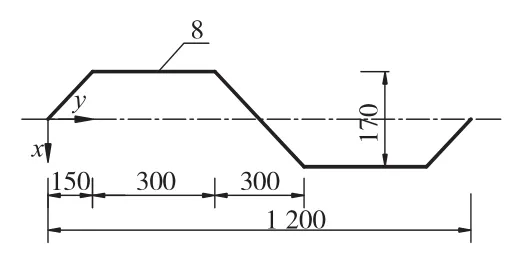
图3 波形钢腹板几何尺寸（单位：mm）

（1）材料参数：顶、底板采用C50混凝土，弹性模量Ec=3.45×104MPa，泊松比υ=0.2；腹板采用波纹钢腹板，钢板弹性模量Es=2.1×105MPa，泊松比υ=0.3；横隔板采用C50混凝土，端横隔板厚300 mm，中横隔板厚200 mm。

（2）边界条件：一端为固定铰支承，限制底板与腹板相交节点上的3个平动自由度，包括径向ux、切线uy、竖向uz；另一端为活动铰支承，仅限制底板与腹板相交节点上竖向平动自由度uz。

（3）单元类型：曲线箱梁采用壳单元SHELL93建模，而横隔板采用SHELL63单元进行建模。

（4）中横隔板布置：中横隔板数量为N，横隔板等间距布置，LD=L/（N+1）。

（5）荷载：恒载包括自重和二期恒载，活载是根据《公路桥涵通用设计规范》中最不利车道荷载，按最大弯矩等效集中荷载进行取值。当N为偶数时，偏心荷载P施加在跨中内侧腹板与顶板交点，当N为奇数，荷载施加在跨中附近两个横隔板中间处交点上，如图4所示。

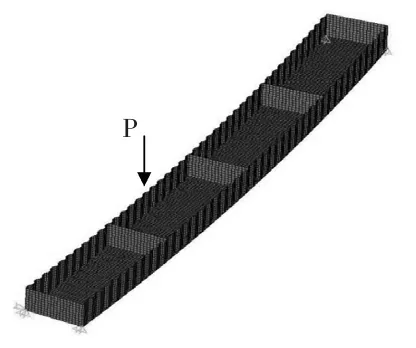
图4 有限元模型示意图

3 数值分析

在偏载和恒载作用下，翘曲正应力最大值一般出现在荷载施加位置截面底板与腹板交界点处，因此取加载截面底板与内侧腹板交点处作为控制点。AASHTO规范等［8-10］给出了横隔板设置一般原则为：将控制点处的翘曲正应力与弯曲正应力的比值控制在10%以内。

横隔板合理间距计算过程如表1所示。从表中可以得出：曲线箱梁随着横隔板数量N=0（LD=51.6 m）增加至N=7（LD=6.5 m），翘曲正应力与弯曲正应力的比值σωT/σMT从20%递减到9%，因此上述算例横隔板合理间距LDR=7.4 m。

波纹钢腹板箱梁合理横隔板间距主要取决于翘曲应力中畸变正应力，对于直线箱梁畸变正应力的影响因素［11］主要有：箱梁外形尺寸及波纹钢腹板尺寸，对于曲线箱梁还需考虑曲率半径变化。因此本文分析了箱梁高宽比H/B、曲率半径R对横隔板间距影响，其中H/B取2/5、1/2、3/5、5/7、4/5，半径取100 m、200 m、300 m、500 m、1 000 m、∞。将波纹钢腹板曲线组合箱梁的合理横隔板间距LDR与H/B、1/R的关系如图5、图6所示。

从图5可知：随着H/B的变大，梁高增加，截面抗弯惯性矩Ix迅速增大，弯矩作用下产生的弯曲正应力迅速减小，而翘曲应力减小幅度相比弯曲应力较小，需要设置的横隔板数量有所增加。合理横隔板间距LDR与H/B可以用线性函数模拟如式（3）所示：

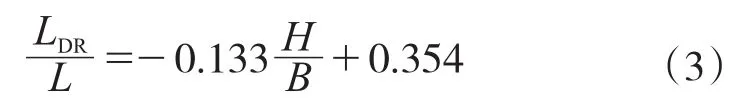
从图6中得出：半径R对波形钢腹板曲线箱梁横隔板合理间距LDR的影响很大，随着R变大，弯扭耦合效应更加明显，无论是在自重作用下还是内侧偏心荷载作用下，扭转产生的翘曲应力将占到弯曲应力的很大比例，需要设置的横隔板数量迅速增加。合理横隔板间距LDR与R可以用指数函数模拟：

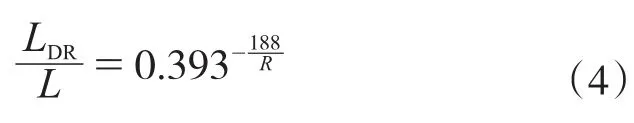
合并公式（3）和公式（4），可得：

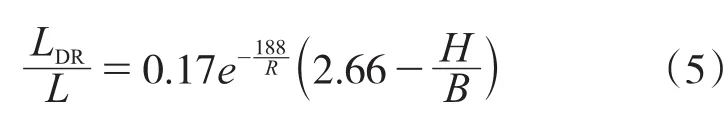
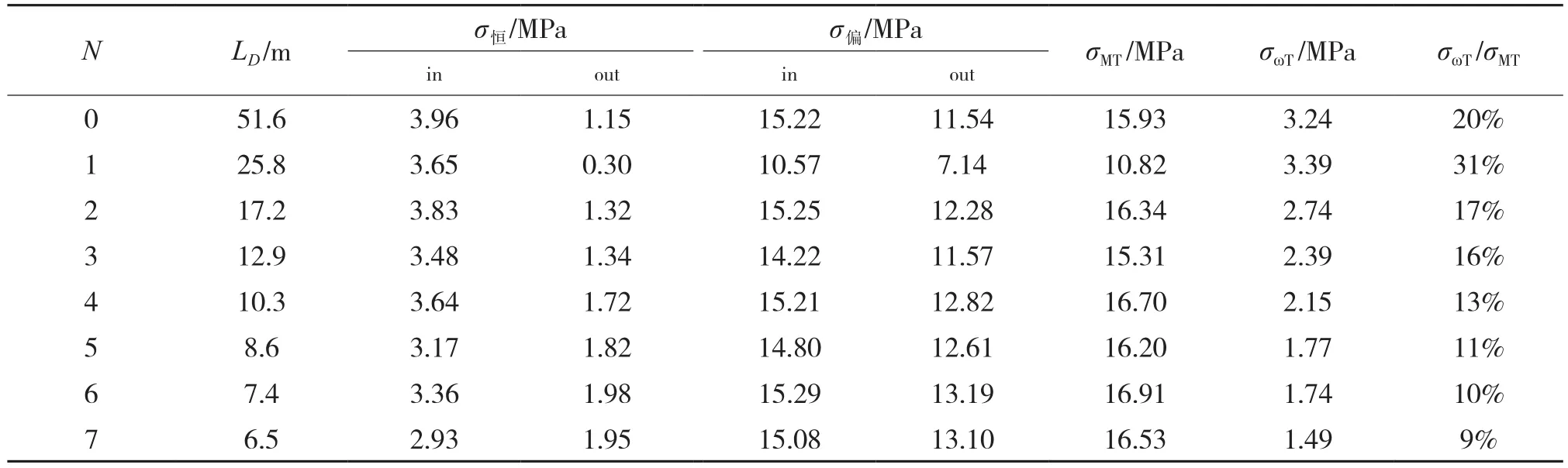
表1 控制点处σωT/σMT随横隔板间距LD变化表

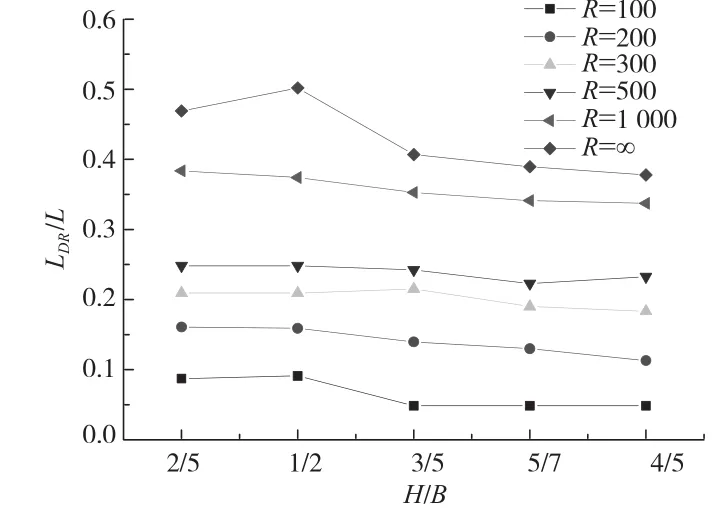
图5 合理横隔板间距LDR与H/B关系图

4 对比分析

为了验证横隔板合理间距估算公式的适用性和安全性，将本文所拟合的经验公式计算结果与实桥横隔板间距对比，结果如表2所示。

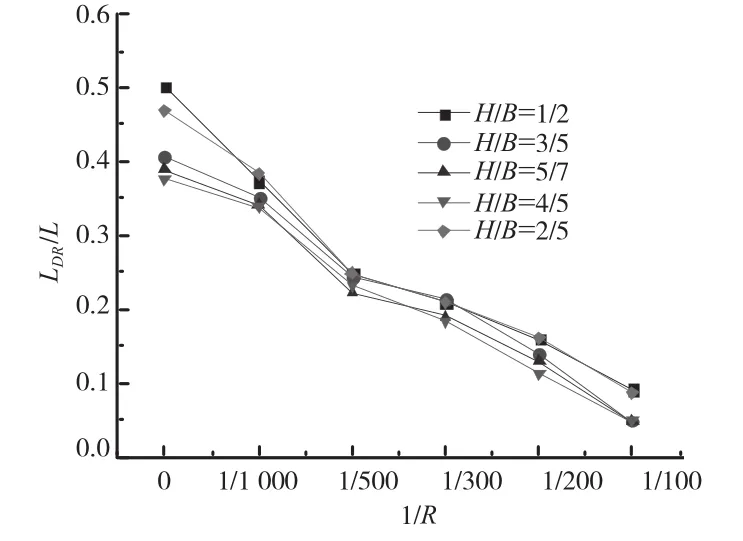
图6 合理横隔板间距LDR与R关系图

表2 实桥横隔板合理间距估算值与实际值对比

对比结果表明：根据式（5）得出的横隔板间距估算值LDR估与实际值LDR实较为接近或者更为保守。其中鱼窝头匝道桥合理横隔板间距估算值LDR估=3.4 m，而实际值LDR实=8.0 m，这是由于单跨圆心角达到26°，弯扭耦合效应明显，产生较大的翘曲正应力，因此需要设置较多数量的横隔板才能将σωT/σMT控制在10%以内，综上所述，按式（5）计算所得的合理横隔板间距安全性、适用性较高。

5 结论

针对波纹钢腹板曲线箱梁相比混凝土箱梁更容易发生畸变变形的问题，采用有限元Ansys进行模拟，通过限制翘曲正应力与弯曲正应力的比值在10%以内，研究曲线箱梁高宽比、曲率半径对横隔板合理间距的影响，模拟出估算公式；对比实桥横隔板合理间距估算值与实际值，结果表明估算公式安全性、适用性较高，可供设计时参考。

［1］侯艳红.波纹钢腹板组合梁的发展及应用［J］.交通科技，2010（6）：1-4.

［2］陈宝春，黄卿维.波形钢腹板PC箱梁桥应用综述［J］.公路，2005（7）：45-53.

［3］李宏江，叶见曙，万水，等.波形腹板箱梁的扭转与畸变分析及试验研究［J］.桥梁建设，2003（6）：1-4.

［4］杨丙文，黎雅乐，万水，等.波形钢腹板箱梁畸变应力分析［J］.东南大学学报(自然科学版)，2011（5）：1065-1069.

［5］韩皓，李彬，瞿尔仁，等.曲线箱梁桥横隔板的加劲作用研究［J］.合肥工业大学学报(自然科学版)，1999（4）：55-59.

［6］李宏江，叶见曙，万水，等.波形钢腹板箱梁横隔板间距的研究［J］.公路交通科技，2004（10）：51-54.

［7］NH Park，YJ Choi，YJ Kang. Spacing of intermediate diaphragms in horizontally curved steel box girder bridges［J］. Finite Elements in Analysis & Design，2005，41（9）：925-943.

［8］余茂峰，刘君波，叶建龙.曲线开口钢箱的扭转变形及横隔板合理间距分析［J］.公路交通技术，2011（4）：63-65.

［9］刘小渝，孙童龄.横隔板对钢箱梁受力畸变的分析［J］.重庆交通大学学报(自然科学版)，2007（5）：9-12.

［10］Manual HS. American association of state highway and transportation officials（AASHTO）［J］. Washington，DC. 2010.

［11］聂细锋，张清华.波形钢腹板组合箱梁扭转及畸变效应关键影响因素研究［J］.四川建筑科学研究，2014（5）：46-49.

Diaphragm Spacing Study of Composite Curved Box-girder with Corrugated Steel Web

Tian Baosheng, Ding Hanshan
（Southeast University, Nanjing 210096, China）

Because the webs of curved box girder with corrugated steel webs have accordion effect, the longitudinal elastic modulus is small. Compared to the concrete box girder, the cross-section with corrugated steel webs may be more prone to distortion deformation, so numbers of diaphragm should be set to reduce cross-sectional distortion. Based on the ratio of sectional warping normal stress to bending stress ratio less than 10%, the influence of the aspect ratio and radius to the diaphragm spacing was studied by Ansys software, fitting the reasonable formula. It has a certain reference value for practical application.

corrugated steel webs; curved box girder; diaphragm; warping normal stress

U443.35

A

1672-9889（2016）06-0036-03

2016-03-09）

国家自然科学基金项目（项目编号：51378106）

田宝升（1990-），男，山东临沂人，硕士，研究方向伟为波形钢腹板组合箱梁扭转性能。