基于CEEMDAN的黄河源区年径流量多时间尺度变化特征研究
2017-01-17丁志宏张金萍赵焱
丁志宏,张金萍,赵焱
(1.天津市中水科技咨询有限责任公司,天津300170;2.郑州大学水利与环境学院,河南郑州450001;3.黄河水利科学研究院水资源研究所,河南郑州450003)
基于CEEMDAN的黄河源区年径流量多时间尺度变化特征研究
丁志宏1,张金萍2,赵焱3
(1.天津市中水科技咨询有限责任公司,天津300170;2.郑州大学水利与环境学院,河南郑州450001;3.黄河水利科学研究院水资源研究所,河南郑州450003)
基于EMD、EEMD和互补EEMD方法的不足之处,将CEEMDAN方法应用于黄河源区唐乃亥水文站1956—2015年的年径流量序列多时间尺度分析,采用纳什效率系数定量评价了各阶模态的重构信号对年径流量序列模拟精度的贡献程度,指出了提高年径流量预测精度的工作方向,揭示了黄河源区水文水资源系统变化的复杂年际特征,解释了20世纪90年代至21世纪初黄河连续枯水时段的成因。
黄河源区;唐乃亥;CEEMDAN;年径流量;多时间尺度;纳什效率系数;枯水时段
DOI
黄河是中华民族的母亲河,以占全国河川径流总量2.2%的天然径流量支撑着全国总人口的12%、耕地总面积的15%,除了承担着本流域的供水任务外,还承担着向流域外的河北省和天津市引黄供水的任务,黄河水资源量的变化对于相关区域社会经济发展具有重大影响。
黄河源区是指黄河从河源至唐乃亥水文站之间的高寒草甸草原区,唐乃亥水文站控制流域面积12.19万km2。黄河源区以占黄河流域面积13%的汇水面积贡献了黄河年径流量的33%,是黄河流域最重要的产流区,素有“黄河水塔”之称,该区域径流量的变化对于整个黄河流域水资源的变化具有至关重要的影响和控制性作用。
径流量的年际变化过程具有多时间尺度性。所谓多时间尺度性,是指径流量的变化在某一时间段内不是只以一种固定的频率(周期、时间尺度)在运动,而是同时包含着各种频率(周期、时间尺度)的变化和局部波动,是包括气象、水文、土壤、植被、社会等各子系统在内的多种动力学机制同时发挥作用的结果,是径流量在时域中呈现复杂变化的根本原因。
综上所述,为深入分析黄河源区年径流量的多时间尺度波动特征,本文运用CEEMDAN方法对黄河源区的控制性水文站——唐乃亥水文站1956—2015年的年径流量序列进行分解,探讨其在各个时间尺度层次上的波动特征,以期为黄河水资源的合理开发、高效利用、有效保护、科学调度等工作提供技术参考和科学依据。
1 CEEMDAN基本理论
为了克服小波变换的诸多不足之处,Huang等人于1998年提出了经验模态分解(Empirical Mode Decomposition,简称EMD)[1]。EMD是一种可以用于分析非线性系统产生的非平稳序列的数据驱动型的适应性方法,它将一个序列分解为局部的、完全数据驱动的、具有快速和慢速波动周期的一系列分量,这些幅度和频率经过调制的分量被称为本征模态函数(Intrinsic Mode Function,简称IMF)。EMD已在水文水资源领域得到了广泛应用[2-4]。
但是,EMD算法的局部特性可能会产生一种被称为模态混淆(混频)的现象:在一个模态中存在具有完全不同的尺度的波动或者在不同的模态中产生具有相似尺度的波动,而理想的情况是每一个模态中的尺度是相似的。为了减轻EMD的模态混淆现象,Huang等人于2009年提出了集合经验模态分解[5](EnsembleEmpiricalModeDecomposition,简称EEMD),该方法是对带有噪声的原始序列的集合进行EMD分解。所谓集合,即是添加了白噪声的原始序列的若干副本,通过求集合的平均值来得到最终分解结果。通过添加白噪声来减少模态混淆是利用了EMD的二值滤波器组特性以及遍布整个时间—频率空间的噪声[6],以此来求得更多的在整个时间跨度内具有相似尺度的更规则的模态。尽管EEMD被证明可以大幅减少混频现象并在水文水资源等领域得到了广泛应用[7-9],然而,该方法在解决旧问题的同时也产生了新问题:在EEMD的重构序列(即所有模态之和)中存在着残留噪声,另外,EEMD的每一次EMD分解所产生的模态的个数可能是不同的,这使得最终在求集合平均值时变得困难。为了解决EEMD存在的问题,Huang等人于2010年提出了互补EEMD[10](Complementary Ensemble Empirical Mode Decomposition,简称互补EEMD),即通过使用互补噪声对(即增加和减去相反的白噪声)减轻了重构序列存在的噪声残留问题。然而,互补EEMD的数学完整性不能被证明,而且最终在求集合平均值时存在的问题依然没有得到解决,因为互补EEMD依旧会产生每一次EMD分解所产生的模态的个数可能会不同这一问题。
2011年,Torres等人提出了具适应性噪声的完全集合经验模态分解[11](Complete Ensemble Empiri⁃cal Mode Decomposition with Adaptive Noise,简称CEEMDAN),对EEMD进行了重要改进,解决了EEMD存在的上述两个问题并在多个领域得到了应用[12-14]。2014年,Torres等人又对CEEMDAN进行了改进[15],完美解决了CEEMDAN初始算法[11]所存在的个别模态包含残留噪声以及分解早期可能存在虚假模态等两个问题。
综上所述,CEEMDAN是在EMD和EEMD的基础上发展而来的,本文按照技术发展历程来对CEEMDAN[15]的基本理论介绍如下:
EMD是把1个序列分解为若干数目的IMF,而IMF必须满足2个条件:①极值点(极大值和极小值)的个数和跨零点的个数必须相等或者至多相差1个;②局部平均值,即上包络线和下包络线的平均值,必须为0。EMD算法具体参见文献[1]。
EEMD把相应的IMF的平均值定义为“真实”模态,这些IMF是通过向原始序列中添加白噪声后再进行EMD分解而得到的。设x() t为待分解序列,EEMD算法可描述如下:
在进行EMD分解时,均需进行不同次数的迭代,迭代终止与否的判断指标采用限制标准差SD,SD定义为[1]:式中:h1l(t)为EMD分解时第l次筛选所得的数据;h1(l-1)(t)为EMD分解时第l-1次筛选所得的数据;T为序列长度。

SD的值一般取0.2~0.3,即满足0.2<SD<0.3时分解过程即可结束。采用此标准的物理考虑是:既要使得d(i)k足够接近IMF的要求,又要控制分解的次数,从而使得所得IMF分量保留原始序列中的幅值调制信息。
值得指出的是,在EEMD中,每个x(t)(i)都是独立地被分解,对每一个x(t)(i)来说,每一次实现中的每一个分解阶段得到的都是独立的,其间没有关联。
使用噪声辅助技术改进EMD的主要思想是往序列中添加一些可控噪声,以创造新的极值点。使用这种方式,局部平均值被“强迫”吸引在原始序列中的新极值点被创造出来的那些部分,而同时原始序列中的没有新的极值点被创造出来的那些部分没有被改变,即该算法被强迫聚焦到尺度—能量空间的一些特别点上。取平均值就是为了更好地估计局部均值,这些局部均值在原始序列添加噪声后的各个实现中是略有不同的。
然而,EEMD通过取平均值来估计的是模态而不是局部均值。这是因为EEMD是独立地分解每一个具噪声的原始序列,所以在每一次分解的第1个阶段有1个局部均值和1个模态,则真实模态就是具噪声原始序列的EMD分解所求得的模态的平均,这其中就包含着一些残余噪声。这就造成EEMD存在以下问题:①分解是不完全的,即存在重构误差;②每一次所得的模态个数可能会不同,造成最后求集合的平均值时存在困难。
在互补EEMD中,噪声是成对地被添加到原始序列上(一个是正的,一个是负的),由此产生2个集合:式中:y(i)为具噪声的原始序列的具有互补性的2个副本;x(t)和w(i)同前。

尽管这一方法显著减小了重构序列中的残余噪声,但是仍然不能保证和会产生相同数目的模态,使得最后的求平均值还是存在困难,同时模态中仍然存在噪声残余。
CEEMDAN的具体算法为:令Ek(⋅)为通过EMD产生第k阶模态的算子,令M(⋅)为产生将要被进行分解的序列的局部均值的算子,令w(i)为均值为零、方差为1的白噪声,是在实现中求取平均值的算子,可以看出E1(x)=x-M(x),则:
(1)使用EMD计算x(i)=x+β0E1(w(i))(即x的第i次实现)的局部均值,以求得第1个残差:

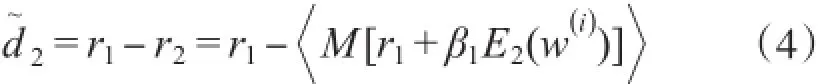
(4)对于k=3,…,K,计算第k个残差:

(5)计算第k阶模态:

(6)返回第4步计算下一个k。
重复进行第4步至第6步直到所求得的残差满足以下条件之一为止:①不能被EMD进一步分解为止;②满足IMF条件;③局部极值点的个数小于3个。
综上,经CEEMDAN重构,最终残差满足:

K是模态的总阶数。因此,原始序列x可以表达为:

上述分解过程确保了CEEMDAN的完整性并因此保证了原始序列得以准确重构。模态的最终阶数只取决于原始序列数据和停止准则。系数βk=εkstdrk允许在每一个阶段进行信噪比(SNR)选择。在EEMD中,噪声和残差之间的信噪比SNR随着阶数k的增加而增加,这是因为当k>1时,第k阶残差中的能量只是在计算开始时所添加的噪声能量的若干分之一。为了模拟这种现象,CEEMDAN将ε0设置为初始噪声和原始序列的理想信噪比SNR的倒数:若将SNR表达为标准差的商数,则有β0=ε0std(x)/std[E1(w()i)],为了获得后续分解阶段中的具有较小波动幅度的噪声实现,在剩余模态中,直接使用其前一步通过EMD进行分解时得到的噪声,不用其标准差来进行归一化处理,即βk=ε0std(rk),k≥1。
所有EMD类方法的由细到粗进行筛分的理论本质决定了其分解所得到的第1阶模态所揭示的是原始序列中变化最快(频率最高、周期最短)的序列分量。
2 实际应用
2.1 基本资料选用
本文分析选用唐乃亥水文站1956—2015年的年径流量序列,如图1所示。
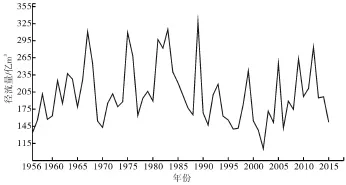
图1 唐乃亥站年径流量序列
2.2 年径流量的CEEMDAN分解
运用CEEMDAN方法[15]对图1所示的唐乃亥站年径流量序列进行多时间尺度分解,实现次数取200,限制标准差SD的取值为0.25,分解结果如图2—5所示。
由图2—5可知:
(1)CEEMDAN将唐乃亥站1956—2015年的年径流量序列分解为4阶模态,其中包括3个IMF分量(图2—4)和1个趋势项Res分量(图5),反映了黄河源区产汇流系统变量演化的复杂多时间尺度性。
(2)第1阶模态IMF1是振幅最大、周期最短、频率最高的一个波动,依次下去的其他各阶模态的振幅逐渐减小、周期逐渐变长、频率逐渐降低。
(3)第1阶模态IMF1具有准2~7 a波动周期,以准2~4 a波动周期为主,在60 a的观测时段内其平均振幅34.35亿m3,最大振幅75.19亿m3,最小振幅1.90亿m3。

图2 唐乃亥站年径流量序列的IMF1分量

图3 唐乃亥站年径流量序列的IMF2分量
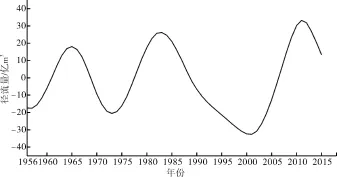
图4 唐乃亥站年径流量序列的IMF3分量
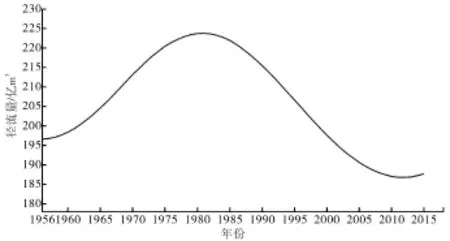
图5 唐乃亥站年径流量序列的Res分量
(4)第2阶模态IMF2具有准5~10 a波动周期,以准7 a波动周期为主,在60 a的观测时段内其平均振幅36.79亿m3,最大振幅57.27亿m3,最小振幅2.64亿m3;自1967—1982年为高幅振荡时段,平均振幅51.86亿m3,最大振幅57.27亿m3,最小振幅44.37亿m3;自1982—1998年为低频振荡时段,最大波动周期为准10 a。
(5)第3阶模态IMF3具有准18 a和准28 a波动周期,在60 a的观测时段内其振幅呈增加趋势,平均振幅26.40亿m3,最大振幅33.59亿m3,最小振幅18.74亿m3。
(6)第4阶模态Res分量显示的是唐乃亥站年径流量的整体变化趋势,1977和2008年是Res曲线的2个拐点,1951—1977年唐乃亥站年径流量整体呈增加趋势,增幅为14.36%;1977—2008年唐乃亥站年径流量整体呈减小趋势,减幅为16.54%;自2008年开始唐乃亥站年径流量整体又呈增加趋势,进入新一轮的增长周期。按照目前所展现出来的半个波动周期(1977—2008年)推论,Res分量具有准62 a波动周期。
(7)20世纪90年代至21世纪初,黄河源区出现的、进而导致黄河流域出现的连续枯水时段主要是由于第3阶模态IMF3的异常波动造成的,这是因为若按照90年代之前的波动周期为准18 a的波动规律,该模态应该在1993年出现谷值、2002年出现峰值,但是却在1993年之后继续下行直至在2002年出现谷值,形成一个完整的“逆峰”,又与Res分量的同期下降趋势相叠加,导致黄河出现长达10 a左右的枯水期。
2.3 模态重构精度评价
根据CEEMDAN的分解理论及实际计算,图2—5所示的4阶模态可以完全重构图1所示的实测径流量序列。为了定量评价各阶模态在重构中的作用,采用纳什效率系数(Nash-Sutcliffe efficiency co⁃efficient,简称NSE)来表征不同模态组合和实测径流量序列之间的模拟精度,纳什效率系数的定义为:

NSE的取值范围为负无穷至1,E越接近1,表示模拟质量越好,模型可信度越高;E等于1,表示模型模拟值与实测值完全一致,误差为0;E越接近0,表示模拟结果越接近观测值的平均值水平,即模型总体结果可信,但过程模拟误差大;E远远小于0,则表明模型的模拟结果是不可信的。
以图1所示径流量序列作为实测值、图2—5所示的4阶模态的依次组合作为模拟值,分别计算其NSE值,结果如图6—8所示。

图6 唐乃亥站年径流量实测值与2、3、4阶模态重构值的比较

图7 唐乃亥站年径流量实测值与3、4阶模态重构值的比较

图8 唐乃亥站年径流量实测值与模态4的比较
从图6—8可知:
(1)第2、3、4阶模态重构所得的序列与实测径流量序列之间的NSE为0.56,则第1阶模态对重构实测值的模拟精度贡献率为0.44。
(2)第3、4阶模态重构所得的序列与实测径流量序列之间的NSE为0.27,则第2阶模态对重构实测值的模拟精度贡献率为0.29。
(3)第4阶模态与实测径流量序列之间的NSE为0.06,则第4阶模态对重构实测值的模拟精度贡献率为0.06,同时也说明第4阶模态作为实测径流量序列的平均值是有统计意义的,符合NSE的定义,证明CEEMDAN分解理论和计算结果的正确性。
(4)周期越短、振幅越大、频率越高的模态在重构中的作用越是突出,对模拟精度的提高贡献越大;但是,必须指出的是,这种贡献的作用是相对的,是建立在作为平均值的第4阶模态得以准确模拟的基础之上的,若无第4阶模态以及第3阶模态作为基础,第1阶和第2阶模态等高频模态对原始序列的模拟精度将会出现数量级的误差。由此可知,高频模态是刻画序列变化的细节和局部,低频模态则掌控着序列变化的全局和趋势。
3 结语
在分析EMD、EEMD和互补EEMD方法不足之处的基础上,将CEEMDAN方法应用于黄河源区唐乃亥水文站1956—2015年的年径流量时序的多时间尺度分析并采用纳什效率系数定量评价了各阶模态在模拟实测径流信号的重构中的精度贡献率,结果表明唐乃亥站年径流量分别具有准2~7 a、准5~10 a、准18 a、准28 a、准62 a的波动周期;黄河源区在20世纪90年代至21世纪初的连续枯水时段是由于第3阶模态的异常波动造成的;在掌握序列趋势变化的基础上提高第1阶模态的预测精度是提高唐乃亥站年径流量预测精度的工作方向;按照各阶模态的周期和振幅所显示的变化趋势,预计自21世纪10年代至中叶的这一时期内,唐乃亥站年径流量将呈现在波动中增加的趋势,黄河源区将进入丰水期,这对于黄河流域水资源开发、利用与保护工作是有利的。
具适应性噪声的完全集合经验模态分解(Com⁃plete Ensemble Empirical Mode Decomposition with Adaptive Noise,简称CEEMDAN)作为EMD和EEMD的最新改进方法,是具有分解完整性、模态精准性等优点的一种全新的非线性、非平稳序列多时间分辨率分析方法,在水文水资源领域的分析、建模和预测中具有广阔的应用前景。
[1]Huang N E,Shen Z,Long S R,et al.The empirical mode de⁃composition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society A:Mathematical,Physical and Engineering Sci⁃ences,1998,454:903-995.
[2]冯平,丁志宏,韩瑞光,等.基于EMD的降雨径流神经网络预测模型[J].系统工程理论与实践,2009,29(1):152-158.
[3]Zhang Jinping,Ding Zhihong,Yuan Wenlin,et al,Research on the relationship between rainfall and reference crop evapo⁃transpiration with multi-time scales[J].Paddy and Water En⁃vironment,2013,11(1-4):473-482.
[4]赵文刚,邢旭光,马孝义.基于EMD方法的土壤入渗空间异质性及其影响因素研究[J].灌溉排水学报,2016,35(3):61-67.
[5]Wu Z,Huang N E.Ensemble empirical mode decomposition: a noise-assisted data analysis method[J].Advances in Adap⁃tive Data Analysis,2009,1(1):1-41.
[6]Flandrin P,Rilling G,Goncalvès P.Empirical mode decompo⁃sition as a filter bank[J].IEEE Signal Process,LETT,2004,11(2):112-114.
[7]王兵,李晓东.基于EEMD分解的欧洲温度序列的多尺度分析[J].北京大学学报(自然科学版),2011,47(4):627-635.
[8]安学利,潘罗平,张飞.基于EEMD和近似熵的水电机组摆度去噪方法[J].水力发电学报,2015,34(4):163-169.
[9]Ouyang Qi,Lu Wenxi,Xin Xin,et al.Monthly Rainfall Fore⁃castingUsingEEMD-SVRBasedonPhase-SpaceReconstruc⁃tion[J].WaterResourcesManagement,2016,30:2311-2325.
[10]Yeh J R,Shieh J S,Huang N E.Complementary ensemble empirical mode decomposition:a novel noise enhanced data analysis method[J].Advances in Adaptive Data Analysis,2010,2(2):135-156.
[11]Torres M E,Colominas M A,Schlotthauer G,et al.A com⁃plete ensemble empirical mode decomposition with adaptive noise[A].Prague,Czech:IEEE International Conference on Speech and Signal Processing(ICASSP),2011:4144-4147.
[12]Antico Andrés,Torres María E,Diaz Henry F.Contributions of different time scales to extreme Paraná floods[J].Clim⁃mate Dynamics,2016,46:3785–3792.
[13]Han J,Bann M.Van der.empirical mode decomposition for seismic time-frequency analysis[J].Geophysics,2013,78(2):9-19.
[14]韩庆阳,孙强,王晓东,等.CEEMDAN去噪在拉曼光谱中的应用研究[J].激光与光电子学进展,2015,52(11):274-280.
[15]Colominas M A,Schlotthauer G.,Torres M.E.Improved com⁃plete ensemble EMD:A suitable for biomedical signal pro⁃cessing[J].Biomedical Signal Processing and Control,2014,14(11):19-29.
TV121
A
1004-7328(2016)06-0001-06
2016—07—12
国家自然科学基金项目(51309202);水利部公益性行业科研专项经费项目(201101016)
丁志宏(1979—),男,博士,高级工程师,主要从事水文水资源研究与咨询工作。
