模糊数学综合评价法在潘家口水质评价中的应用

赵建河，高峰，刘英英，段龙飞，吕艳

（1.海河水利委员会引滦工程管理局，天津300393；2.天津武警后勤学院数学教研室，天津300309）

模糊数学综合评价法在潘家口水质评价中的应用

赵建河1，高峰1，刘英英2，段龙飞1，吕艳1

（1.海河水利委员会引滦工程管理局，天津300393；2.天津武警后勤学院数学教研室，天津300309）

以潘家口水库潘坝上断面为例，利用模糊综合评价模型对该断面2014年全年的5个重要水污染因子进行评价分析，避免了在水质评价中因单因子评价法经常会遇到的亦此亦彼的模糊概念及单因子评价过高而影响整体水质评价过高的问题，为制定潘家口水库水环境保护政策和水污染防治规划提供借鉴。

水质评价；综合评价法；潘家口水库

1 引言

潘家口水库位于河北省迁西县城北27 km处，是滦河干流上游第一座大型水库，是天津、唐山两市重要的饮用水源地，担负着向津、唐地区提供工农业用水和人民生活用水任务，为津、唐地区的经济发展和人民生活水平的提高作出了重大贡献。随着水库上游地区的快速发展以及水库网箱养鱼数量日益增多等多方面因素影响，潘家口水库水质状况日趋下降，水体富营养化程度逐年升高，从而对水体评价造成极大影响。笔者以潘家口水库潘坝上断面为例，利用模糊数学中的隶属度概念，重新对潘家口水库水体进行评价，以解决因单因子评价过高而出现的影响整体评价的问题。

2 模糊数学综合评价法及其主要步骤

模糊综合评价法是一种基于模糊数学的综合评价方法。该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象作出一个总体的评价。

2.1 建立因子集

影响水质的因素有很多，根据潘家口水库水质影响的实际情况及监测条件，选取潘家口水库潘坝上断面的COD、氨氮、总氮、总磷、六价铬作为主要因子，建立如下因子集：{U=COD,氨氮,总氮,总磷,六价铬

2014年各因子监测数据，见表1。

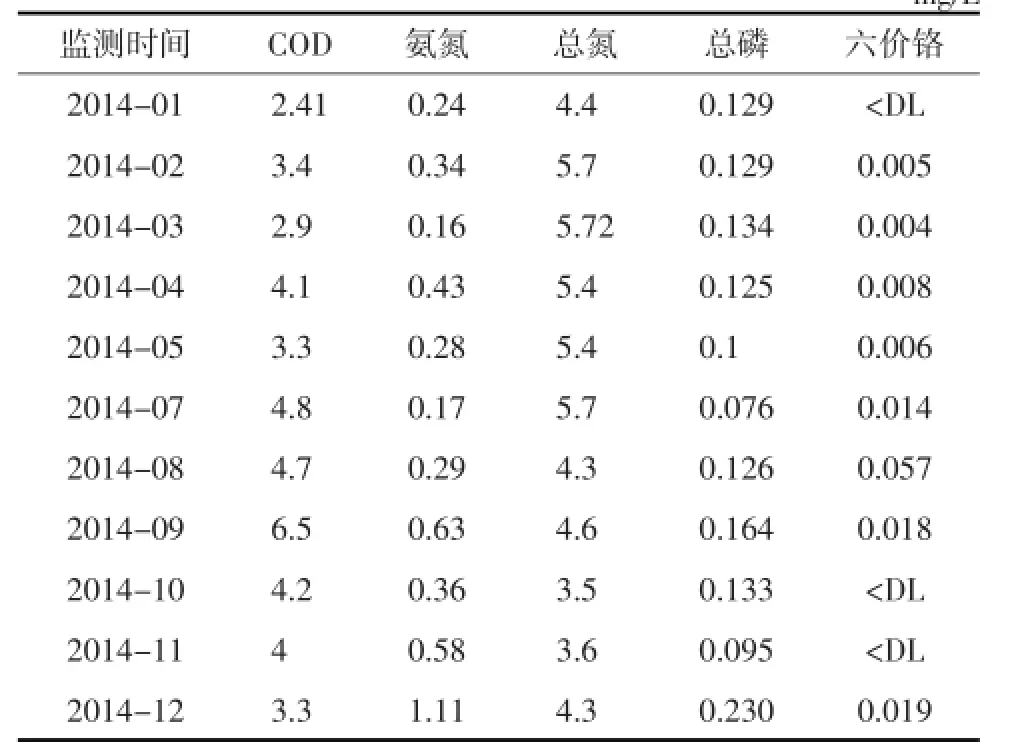
表12014年各因子监测数据

2.2 建立评价集

在模糊数学中，评价集一般可表示为：V={v1,v2,…,vn}。根据地表水质量评价等级以及潘家口水库水质评价实际情况，分为如下5个模糊等级：，各项指标参考值见表2。

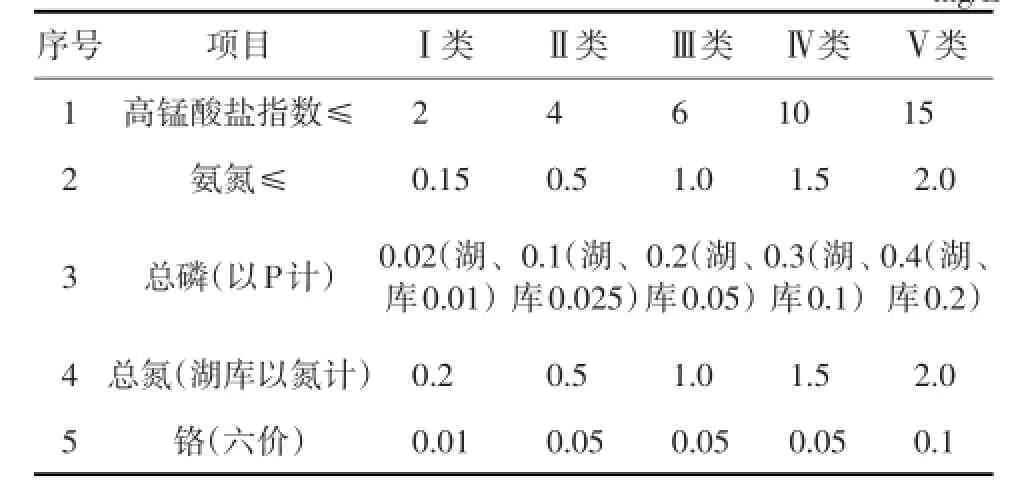
表2 地表水环境质量标准基本项目标准限值

2.3 建立隶属函数和模糊关系矩阵

水污染情况是一个模糊数学问题，隶属函数是模糊数学综合评价法的一项重要内容，直接影响到评价结构的准确性。确定隶属函数的方法很多，笔者选取降半梯形分布函数法来确定隶属函数，其一般表达式如下：

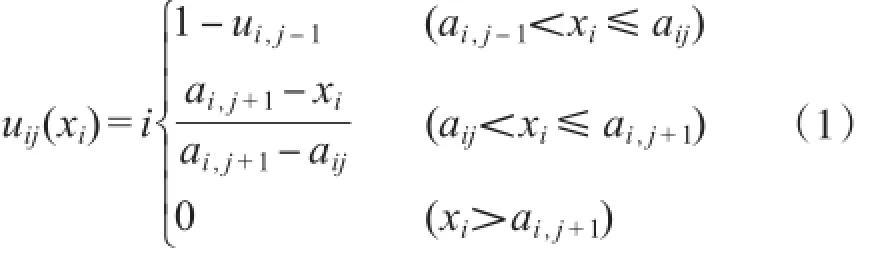
式中：xi为第i个评价因子的监测值；aij为第i个评价因子所对应的第j级评价标准值；i,j=1,…,5。对于xi，当xi≤ai1时，ui1(xi)=1；其余条件下，uij(xi)=0。

计算各评价因子隶属度，建立评价矩阵：

2.4 确定各因素的权重

一般来说，各个因子在评价中有不同的重要性，因此对各因子ui按其重要程度赋予不同的权重，组成权数矩阵：，其中ωi为第i个评价因子的权重。对于数值越大污染越严重的因子，对于数值越小污染越重的因子，在将矩阵W标准化后得到矩阵A。

2.5 建立水质评价模型，计算评价结果

模糊综合评价结果为：Y=A·R=(Y1,Y2,Y3,Y4,Y5)。

这是评价等级集合上的一个模糊子集。经计算，得出模糊数学法计算结果，见表3。

表3 模糊数学法计算结果

3 结语

由表3可以看出，利用模糊数学评价法可以更加直观地看出污染物因子在各因子中所占的权重比，也符合传统评价法对水质评价的整体趋势，同时还充分考虑了多个因子对水体的影响，在一定程度上避免了水污染程度的模糊性带来的人为主观判断以及单个因子过高引起的水质评价过高的问题。

X824；TV62+2

A

1004-7328（2016）06-0063-02

10.3969/j.issn.1004-7328.2016.06.020

2016—07—25

水利部科技推广项目（SF-201605）

赵建河（1962—），男，高级工程师，主要从事水利工程运行管理和水资源保护工作。