四元数矩阵右特征值的范围估计
2017-01-17韩俊佳畅大为叶绒绒
韩俊佳,畅大为,叶绒绒
(陕西师范大学 数学与信息科学学院,陕西 西安 710119)
四元数矩阵右特征值的范围估计
韩俊佳,畅大为,叶绒绒
(陕西师范大学 数学与信息科学学院,陕西 西安 710119)
讨论一个n×n阶四元数矩阵的所有右特征值的范围.对已有圆盘定理的条件加以改进,从而得到对于任意一个右特征值λ,只要存在η∈[λ],且有|λ-aii|=|η-aii|,则所有右特征值都在圆盘的并集内.另外还给出了四元数矩阵的所有右特征值或者所有主对角线元素都是实数情况下的结论.数值例子说明所得定理结论对一般情况仍成立.
四元数;四元数矩阵;右特征值;特征向量
0 引 言
1843年,爱尔兰数学家汉密尔顿在将复数推广到更高维数时提出了四元数的概念.四元数在计算机科学和量子力学等领域起着重要的作用.因为四元数能表示四维空间中的量,因而也常用于机械视觉以及视频游戏和控制航天器中[1-2].
近年来,四元数问题备受学者关注并得到广泛研究[3-7].而研究四元数和四元数矩阵的主要问题就是四元数乘积的不可交换性[8-9].一个四元数问题的结果、解决方案或结论与复数情况时有很大不同[10-12].例如,对于复数矩阵不区分左、右特征值,实际上它们是相等的.而对于四元数矩阵就要分别讨论其左、右特征值,在一般的情况下它们区别很大.文献[8] 中的四元数矩阵的一个左特征值不是它的右特征值且四元数矩阵的左右特征值的个数不相等.
文献[13-17]给出的适用于2×2四元数矩阵的所有左特征值的圆盘定理,在大多数情况下并不适用于右特征值;而给出的适用于四元数矩阵右特征值的圆盘定理并不能包含四元数矩阵的所有右特征值,只是说明由所有右特征值构成的集合与n个圆盘的并集有交集.本文在此基础上,加上一个条件,使得满足条件的四元数矩阵的所有右特征值都在n个圆盘的并集内,得到一个应用范围更广的结论.
1 预备知识
一般地,C、R分别表示复数集、实数集.设四元数集
H={a0+a1i+a2j+a3k:a0,a1,a2,a3∈R},
其中i2=j2=k2=ijk=-1.
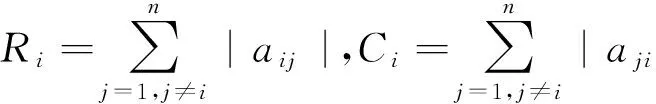
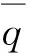
定理1[8]设x为任意四元数,那么有
(2) x*=x当且仅当x∈R.
(3) ∀x∈H,有ax=xa当且仅当a∈R.
(4) 若x≠0,称x*/|x|2为x的逆,记作x-1,且|x-1|=1/|x|.
(5) 任意的四元数x可以被写成x=a1+a2j,其中a1,a2∈C.
定义2[8]对于两个四元数x,y,如果存在一个非零四元数q,使得q-1xq=y,则称x与y 是相似的,记作x~y.
记所有与x相似四元数组成的集合为[x],称为[x]的相似类.若x与y相似,则有|x|=|y|.

例如,i与-j相似,存在q=i-j,使得-j=q-1xq,则有-j∈[i].
特别地,对于任意四元数x,x与x*相似.
定义3[8]设A=(aij)∈Hn×n,A可以写成A=A1+A2j,A1,A2∈Cn×n,称φA为四元数矩阵A 的复伴随矩阵.其中

定义4[8]设A=(aij)∈Hn×n,对于一个四元数λ,如果存在一个非零四元数列向量Y=(y1,y2,…,yn)T,使得AY=Yλ,则称λ为矩阵A的一个右特征值.
特别地,若λ是矩阵A的一个右特征值,则∀q∈[λ]也是A的右特征值.
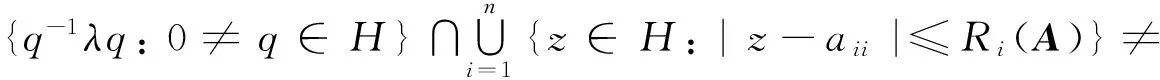
2 主要结论及证明
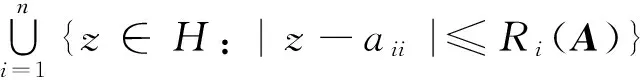
证明 令λ为A 的任意一个右特征值,0≠ X=(x1,x2,…,xn)T∈Hn×1是对应于λ的特征向量,即AX=Xλ.设|xt|=max|xi|,i=1,2,…,n,则有|xt|≠0.若存在η, 使得ηxt=xtλ,就有η∈[λ].因此由AX=Xλ得
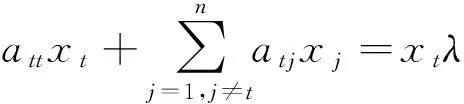
则有
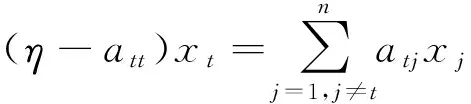
从而有
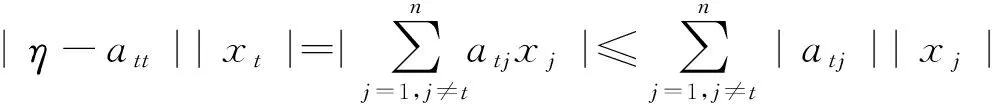
因此
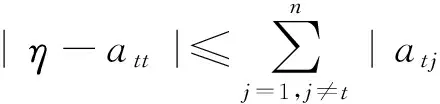
又由|λ-aii|=|η-aii|得
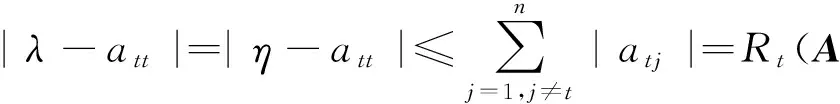
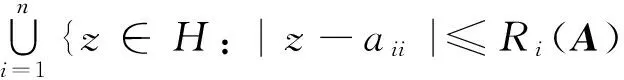
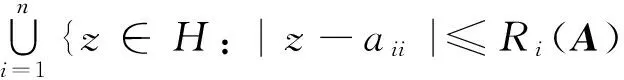
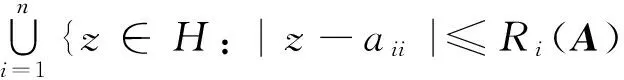
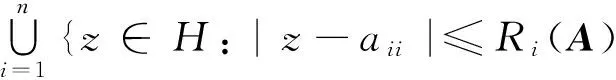
证明 若矩阵A的每一个右特征值λ,都有λ∈R,则∀γ∈[λ],都有|λ-aii|=|γ-aii|.因此由定理4知结论成立.
注 推论1与推论2为定理3的两个特殊情况.定理3给出了能包含四元数矩阵所有右特征值的一个集合,比文献[13]中定理7的结论更好.
定义5[18]对于两个矩阵A∈Hn×n和B∈Hn×n,如果存在P∈Hn×n,使得A=P-1BP,则称A与B相似,记作A≈B.
引理2[18]设A∈Hn×n,则有A≈ A*.
引理3[18]设A∈Hn×n和B∈Hn×n,若A与B相似,则它们有一样的右特征值.
由上面的引理,可得如下定理.
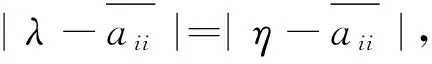
证明 设λ为A的任意一个右特征值,由引理2和引理3知,λ也为A*的一个右特征值.设0≠X=(x1,x2,…,xn)T∈Hn×1为矩阵A*的对应与λ的一个特征向量,即A*X=Xλ.令|xt|=max|xi|,i=1,2,…,n,则|xt|≠ 0.于是有
令ηxt=xtλ,η∈[λ],则
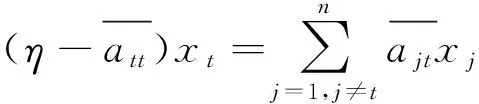
就有

即
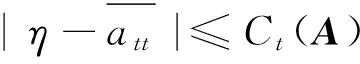
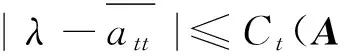
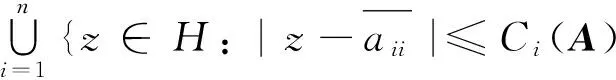
同理可得以下结论.
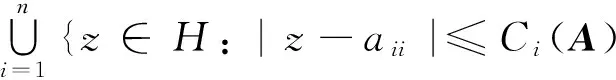
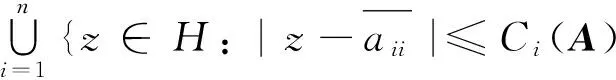
证明 若矩阵A的每一个右特征值λ,都有λ∈R,则∀γ∈[λ],都有|λ-aii|=|γ-aii|.因此由定理5知结论成立.
注 推论3和推论4为定理5的两个特殊情况.定理5给出了能包含四元数矩阵所有右特征值的一个集合比文献[18]中定理3.2的结论要好一些.
以上推论分别为定理4和定理5的特殊情况,下面举例说明定理4和5对于一般情况仍然成立.
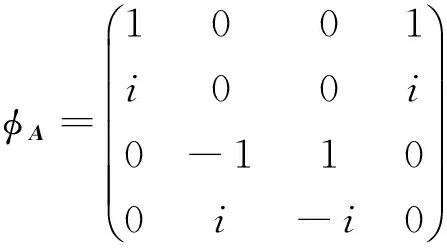
由det(λI-φA)=0得,A的右特征值为0和{q-1(1+i)q: q∈H}.
对于一个右特征值λ=1+i,存在η=1+j∈[λ],使得|1+i-1|=|1+j-1|,|1+i-k|=|1+j-k|,|1+i+k|=|1+j+k|. 此处R1=1,R2=1,C1=1,C2=1则有1+i∈{z∈H: |z-1|≤1}∪{z∈H: |z-k|≤1},1+i∈{z∈H:|z-1|≤1}∪{z∈H:|z+k|≤1}.
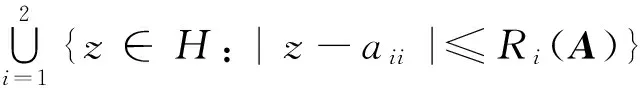
3 结束语
本文对四元数矩阵的右特征值加以条件限制,即对四元数矩阵的任意一个右特征值,只要存在一个四元数与其相似且他们与矩阵的任意一个主对角线元素之差的模相等,则四元数矩阵的所有右特征值都在n个圆盘的并集内.另外本文讨论的四元数矩阵的阶数是有限的,目前只能准确地计算出2×2阶四元数矩阵的左、右特征值,而3×3阶或者更高阶的四元数矩阵的左、右特征值的精确值计算方法还有待进一步研究.
[1] FINKELSTEIN D R,JAUCH J M,SCHIMINOVICH S,et al.Foundations of quaternion quantum mechanics[J].Journal of Mathematical Physics,1962,3(2):207-220.
[2] ADLER S L,FINKELSTEIN D R.Quaternionic quantum mechanics and quantum fields[M].New York:Oxford University Press,1995:58-60.
[3] HUANG Liping,SO Wasin.Quadratic formulas for quaternions[J].Applied Mathematics Letters,2002,15(15):533-540.
[4] NIVEN Ivan.Equations in quaternions[J].American Mathematical Monthly,1941,48(10):654-661.
[5] WOOD R M W.Quaternionic eigenvalues[J].Bulletin of the London Mathematical Society,1985,17(2):137-138.
[6] WU Junliang,ZOU Limin,CHEN Xiangping,et al.The estimation of eigenvalues of sum,difference, and tensor product of matrices over quaternion division algebra[J].Linear Algebra and its Applications,2008,428(11/12):3023-3033.
[7] HUANG Liping.On two questions about quaternion matrices[J].Linear Algebra and its Applications,2000,318(1):79-86.
[8] ZHANG Fuzhen.Quaternions and matrices of quaternions[J].Linear Algebra and its Applicayions,1997,251(2):21-57.
[9] FARENICK Douglas R.The spectral theorem in quaternions[J].Linear Algebra and its Applications,2003,371(2):75-102.
[10] FARID F O,WANG Qingwen,ZHANG Fuzhen.On the eigenvalues of quaternion matrices[J].Linear and Multilinear Algebra,2011,59(4):451-473.
[11] SO Wasin.Quaternionic left eigenvalue problem[J].Southeast Asian Bulletin of Mathematics,2005,29(3):555-565.
[12] HUANG Liping,SO Wasin.On the left eigenvalues of a quaternionic matrix[J].Linear Algebra and its Applications,2001,323(1):105-116.
[13] ZHANG Fuzhen.Gergorin type theorems for quatrnionic matrices[J].Linear Algebra and its Applications, 2007,424(1):139-153.
[14] WU Junliang.Distribution and estimation for eigenvalues of real quaternion matrices[J].Computer and Mathematics with Application,2008,55(9):1998-2004.
[15] WU Junliang,ZHANG Yan.Estimate for the lower bound of rank and the upper bound of eigenvalues norms' sum of given quaternion matrix[J].Computer and Mathematics with Application,2010,59(9):3160-3166.
[16] AHMAD Sk Safique,ALI Istkhar.Localization theorems for eigenvalues of quaternion matrices[J].Mathematics,arXiv:1502.08014[math.RA].
[18] ZOU Limin,JIANG Youyi,WU Junliang.Location for the right eigenvalues of quaternion matrices[J].Journal of Applied Mathematics and Computing,2012,38(1):71-83.
编辑、校对:师 琅
Location for the right eigenvalues of quaternion matrices
HANJunjia,CHANGDawei,YERongrong
(School of Mathematics and Information Science, Shaanxi Normal University, Xi′an 710119, China)
The location for all the right eigenvalues of an×nquaternionic matrix is discussed.According to the Geršgorin type theorem that has been given,it gets a better conclusion that for every right eigenvalueλ,all the right eigenvalues are containned in the union of the Geršgorin balls if there exists a quaternionη∈[λ] and |λ-aii|=|η-aii|.In additon,the conclusions when all the right eigenvalues or the elements of main diagonal of a quaternionic matrix are given.Finally,it gives a numerical examples to prove the conclusion to be correct in general.
quaternion;quaternion matrices;right eigenvalue;eigenvector
1006-8341(2016)04-0491-05
10.13338/j.issn.1006-8341.2016.04.013
2016-05-21
国家自然科学基金资助项目(60671063)
畅大为(1963—),男,陕西省西安市人,陕西师范大学副教授,研究方向为数值线性代数.
E-mail:dwch@sina.com
韩俊佳,畅大为,叶绒绒.四元数矩阵右特征值的范围估计[J].纺织高校基础科学学报,2016,29(4):491-495.
HAN Junjia,CHANG Dawei,YE Rongrong.Location for the right eigenvalues of quaternion matrices[J].Basic Sciences Journal of Textile Universities,2016,29(4):491-495.
O 241.6
A
