M-矩阵性质的注记

张瑞霞,任芳国

(陕西师范大学 数学与信息科学学院,陕西 西安 710062)

M-矩阵性质的注记

张瑞霞,任芳国

(陕西师范大学 数学与信息科学学院,陕西 西安 710062)

首先利用M-矩阵的基本性质,讨论了M-矩阵乘积及凸组合特性,获得关于M-矩阵乘积及凸组合的相关结论;随后通过比较矩阵及非负矩阵的性质,探讨了矩阵的逆及行列式性质,推导出了M-矩阵的不等式关系.

M-矩阵;非负矩阵;比较矩阵;行严格对角占优阵

1 引言及预备知识

M-矩阵是一类重要的特殊矩阵,它在经济学、运筹学等领域有着广泛的应用.M-矩阵是由Ostrowski在1937年首次提出的,作为矩阵理论的一个研究分支和方法,关于M-矩阵的研究一直备受关注[1-3].文献[4-8]讨论了M-矩阵的性质，得出了一些关于M-矩阵的不等式，文献[9-13]讨论了逆M-矩阵的不等式及其相关不等式,文献[14-16]研究了非负矩阵和M-矩阵之间的关系.文献[17-18]研究了M-矩阵以及逆M-矩阵的主子式的问题.在此基础上,本文主要讨论M-矩阵的乘法性质及凸组合性质,得出关于M-矩阵的一些结果.

为了叙述方便,对符号进行如下约定:Mn(R)表示实数域R上的所有n×n阶矩阵的集合;AT表示矩阵A的转置,|A|表示n阶方阵(|aij|),ρ(A)表示矩阵A的谱半径,其中A=(aij)∈Mn(R);设A=(aij)∈Mn(R),如果aij≥0,则称A为非负矩阵,记作A≥0;设A=(aij)n,B=(bij)n∈Mn(R),如果B-A≥0,称B控制A,记作A≤B.其他未加说明的符号参见文献[1].

下面是与本论文有关的几个定义及引理.

定义1[1]设Zn={A=(aij)∈Mn(R)|aij≤0,i≠j,i,j=1,2,…,n},称Zn中的矩阵A为Z-矩阵.

定义2[1]若A∈Zn,如果A是正稳定矩阵,称A是M-矩阵.

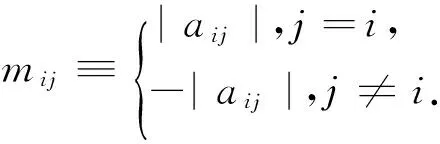
定义4[1]设A∈Mn(R),如果A的比较矩阵M(A)是M-矩阵,称A是H-矩阵.

引理1[1]若A∈Zn,则下列条件互相等价:

(1) A是M-矩阵;

(2) A=αI-P,P≥0,α>ρ(P);

(3) A是非奇异的,且A-1≥0;

(4) 存在正对角矩阵D,使得DA+ATD正定;

(5)A的主对角元素是正的且存在正对角矩阵D,使得AD是行严格对角占优阵;

(6) 存在正向量x>0,使得Ax>0;

(7) AT是M-矩阵.

引理2[1]A,B∈Zn是给定的矩阵,假设A=[aij]是M-矩阵,且B≥A.则

(1) B是M-矩阵;

(2) A-1≥B-1≥0;

(3) detB≥detA>0.

引理3[2]设A=(aij)n,B=(bij)n∈Mn(R)且B是非负矩阵,如果A≤B,则有ρ(A)≤ρ(B).

2 主要结果

定理1 设A∈Mn是M-矩阵,D∈Mn(R)是正对角矩阵,则DA和AD也是M-矩阵.

证明 (1) 首先证DA是M-矩阵.由于A∈Mn是M-矩阵且D是正对角矩阵,则DA∈Zn.由于A是M-矩阵,则由引理1中(4)知,存在一个正对角矩阵E,使得EA+ATE正定.此外对于正对角矩阵D,显然ED-1也是正对角矩阵,且有(ED-1)(DA)+(DA)T(ED-1)=EA+ATE正定,于是由引理1中(4)可得,DA是M-矩阵.(2)其次证AD是M-矩阵.设A∈Mn是M-矩阵,由引理1中(7)可知,AT也是M-矩阵.由已证得(1)可知DAT是M-矩阵,因此由引理1中(7)得,(DAT)T=ADT=AD是M-矩阵.综上可知,DA和AD都是M-矩阵.

定理2 设A,B∈Mn是M-矩阵,则

(1) AB是M-矩阵当且仅当AB∈Zn;

(2) 如果A,B是2阶方阵,则AB是M-矩阵.

证明 (1) 若AB是M-矩阵,显然有AB∈Zn;若AB∈Zn,因为A,B∈Mn是M-矩阵,由引理1中(3)得A和B都是非奇异矩阵,且A-1≥0,B-1≥0.因此,(AB)-1=B-1A-1≥0,于是由引理1(3)知,AB是M-矩阵.

注 一般地,两个M-矩阵的乘积不一定是M-矩阵,如

定理3 设A,B∈Mn(R)是M-矩阵,α∈[0,1],则

(1) 若αA+(1-α)B是M-矩阵,则B-1A没有负的实特征值;

(2) 如果B-1A是M-矩阵,则A和B的凸组合是M-矩阵;

(3) B-1A是M-矩阵当且仅当B-1A∈Zn.

证明 (1)假设B-1A有负的实特征值-λ,其中λ>0,即

det(-λI-B-1A)=(-1)ndet(λI+B-1A)=0,

这与αA+(1-α)B是M-矩阵矛盾,因此B-1A没有负的实特征值.

(2) 因为αA+(1-α)B=B(αB-1A+(1-α)I),且A,B都是M-矩阵,所以A∈Zn,B∈Zn,αA+(1-α)B∈Zn.又B-1A是M-矩阵,所以αB-1A+(1-α)I,α∈[0,1]是M-矩阵.又B是M-矩阵,αA+(1-α)B=B(αB-1A+(1-α)I)∈Zn,由定理2知,αA+(1-α)B是M-矩阵.

(3) 必要性.设B-1A是M-矩阵,显然有B-1A∈Zn.

充分性.由于A是M-矩阵,由引理1中(6)知,存在正向量x>0,使得Ax>0.再由B是M-矩阵,知B-1≥0,显然B-1的每一行至少有一个是正数,所以B-1Ax>0,故由引理1中(6)知,B-1A是M-矩阵.

定理4 设A,B∈Zn,且A是M-矩阵,且B≥A,则

(1) B-1A≤I且AB-1≤I,

(2) B-1A和AB-1都是M-矩阵,

(3) 对于所有的α∈[0,1],αA+(1-α)B是M-矩阵,

(4) ∀α∈[0,1],αC+(1-α)I是M-矩阵,其中C=B-1A或C=AB-1,

(5) (αA+(1-α)B)-1≤αA-1+(1-α)B-1,∀α∈[0,1].

证明 (1) 由引理2(1)知,B是M-矩阵,则 B-1≥0,于是由B≥A知,B-1(B-A)≥0且(B-A)B-1≥0,因而有B-1A≤I,且AB-1≤I.

(2) 由已证得(1)知B-1A∈Zn,AB-1∈Zn,此外由于B≥A,即B-A≥0,以及A是M-矩阵知,(B-A)A-1≥0且A-1(B-A)≥0,即A-1B≥I,BA-1≥I,因而A-1B,BA-1都是非负矩阵,再由于(B-1A)-1=A-1B,(AB-1)-1=BA-1及由引理1中(3)知,BA-1与AB-1都是M-矩阵.

(3) 因为A∈Zn,B∈Zn,所以∀α∈[0,1],αA+(1-α)B∈Zn,又因为A≤B,于是有A≤αA+(1-α)B≤B,由引理2中(1)知,αA+(1-α)B是M-矩阵.

(4) 因为C是M-矩阵,所以∀α∈[0,1],αC+(1-α)I∈Zn且有αC+(1-α)I≥αC.当α=0时,显然αC+(1-α)I=I是M-矩阵,当α≠0时,由引理2(1)知,αC+(1-α)I是M-矩阵.

(5) 令G=AB-1,∀α∈[0,1],由于

及B,G,αG+(1-α)I都是M-矩阵且I-G≥0，可知B-1≥0,C-1≥0,(αC+(1-α)I)-1≥0,于是就有αA-1+(1-α)B-1-(αA+(1-α)B)-1≥0,因此(αA+(1-α)B)-1≤αA-1+(1-α)B-1.

定理5 设A,B=[bij]∈Mn(R),如果A是M-矩阵,且M(B)≥A,则有

(1) B是H-矩阵;

(2) B与|B|都是可逆矩阵;

(3) 0≤|B-1|≤A-1;

(4) 0

证明 (1) 由于M(B)∈Zn,又M(B)≥A,则由引理2中(1)知,M(B)是M-矩阵,因此B是H-矩阵.

(2) 因为M(B)是矩阵M-矩阵,由引理1中(5),存在正对角矩阵D使得M(B)D是行严格对角占优.由于

所以BD与|B|D都是行严格对角占优,因而BD与|B|D是可逆矩阵.再由D是可逆阵知,B与|B|都是可逆矩阵.

[1] HORN R A,JOHNSON C R.Topics in matrix analysis[M].Cambridge:Cambridge University Press,1991:112-133.

[2] HENRY M.Nonnegative matrices[M].New York:Wiley-Interscience Publication,1988:36-39；141-163.

[3] BERMAN A,PLEMMONS R J.Nonnegative matrices in the mathematical sciences[M].New York:Academic Press,1994:132-161.

[4] POOLE G,BOULLION T.A Survey onM-matrices[J].SIAM Review,1974,16(4):419-427.

[5] ANDOT.Inequalities forM-matrices[J].Linear and Multilinear Algebra,1980，67(8):291-316.

[6] 张晓东，杨尚骏.M-矩阵的行列式不等式[J].工程数学学报，1996，13(3):107-111.

ZHANG Xiaodong,YANG Shangjun.Inequalities for determinants ofM-matrices[J].Journal of Engineering Mathematics,1996,13(3):107-111.

[7] 杜吉佩,杨尚骏.可逆M-矩阵两个问题的讨论[J].沈阳师范大学学报，2004，22(3):165-168.

DU Jipei,YANG Shangjun.Discuss on two questions of inverseM-matrices[J].Journal of Shenyang Normal University:Natural Science,2004，22(3):165-168.

[8] 赵建中，杨传胜，周本达.M-矩阵的性质与Hadamard-Fisher不等式的注记[J].大学数学 ，2008，24(2):113-117.

ZHAO Jiaozhong,YANG Chuansheng,ZHOU Benda.The properties ofM-matrices and notes aboutM-matrix′s Hadamard inequuality[J].College Mathematics,2008，24(2):113-117.

[9] LEWIN M,NEUMANN M.On the inverseM-matrix problem for (0,1) matrices[J].Linear Algebra and its Applications,1980,30:41-50.

[10] JOHNSON C R.InverseM-matrices [J].Linear Algebra and its Applications,1982,47:195-216.

[11] CHEN Shencan.Inequalities forM-matrices and iverseM-matrices[J].2007，426(2/3):610-618.

[12] NEUMAN M,NUNG Sing Sze.On the inverse mean first passage matrix problem and the inverseM-matrices problem[J].Linear Algebra and its Applications,2011,434(7):1620-1630.

[13] JOHNSON C R,SMITH R L.InverseM-matrices II[J].Linear Algebra and its Applications,2011,435:953-983.

[14] PENA J M.M-matrices whose inverses are totally positive[J].Linear Algebra and its Applications,1995,221:189-193.

[15] MARKHAM T L.Nonnegative matrices whose inverse areM-matrices[J].Proceedings of American Mathematical Society,1972,36(2):326-330.

[16] 朱辉华，刘建州.非负矩阵是逆M-矩阵的充要条件及其[J].湖南理工学院学报，2009，22(2):13-15.

ZHU Huihua,LIU Jianzhou.The necessary and sufficient condition of inverseM-matrices[J].Journal of Hunan Institute of Science and Technology,2009，22(2):13-15.

[17] JOHNSON C R,SMITH R L.Almost principal minors of inverseM-matrices[J].Linear Algebra and its Applications,2001,337:253-265.

[18] BIERKENS J,RAN A.A singularM-matrix perturbed by a nonnegative rank one matrix has positive principal minors; is it D-stable?[J].Linear Algebra and its Applications,2014,457:191-208.

编辑、校对：师 琅

Notes on the properties ofM-matrices

ZHANGRuixia,RENFangguo

(School of Mathematics and Information Science,Shaanxi Normal University,Xi′an 710062,China)

The products and convex combination ofM-matrices are discussed on the base ofM-matrix basic properties, to some conclusion and some properties in these special operations are obtained. The inverse and determinant of matrix are investigated by using the characterization of comparison matrix and nonnegetive matrix,some inequality relationship ofM-matrix are presented.

M-matrix; nonnegative matrix;comparison matrix;strictly row diagonally dominant matrix

1006-8341(2016)04-0419-05

10.13338/j.issn.1006-8341.2016.04.001

2016-07-08

国家自然科学基金资助项目(11471200)

任芳国(1969—),男，陕西省乾县人，陕西师范大学副教授，研究方向为矩阵论.

E-mail:rfangguo@snnu.edu.cn

张瑞霞,任芳国.M-矩阵性质的注记[J].纺织高校基础科学学报,2016,29(4)：419-423.

ZHANG Ruixia,REN Fangguo.Notes on the properties ofM-matrices[J].Basic Sciences Journal of Textile Universities,2016,29(4):419-423.

O 152.21

A