Normality Criterion Concerning Hayman’s Conjecture

Wang Jianping

(Department of Mathematics,Shaoxing University, Shaoxing, Zhejiang 312000)

Normality Criterion Concerning Hayman’s Conjecture

Wang Jianping

(Department of Mathematics,Shaoxing University, Shaoxing, Zhejiang 312000)

In this paper,we investigate the normality and shared value for meromorphic functions related to Hayman’s conjecture and prove a normal criterion which improves some of the previous results of Pang and Zalcman, Hu and Meng, etc.

normal family; shared value; meromorphic function; Nevanlinna’s theory

Chinese Library Classification: O174.5 Document code:A Article D:1008-293X(2016)09-0024-04

1 Introduction and Results

It is assumed that the reader is familiar with the standard notations such asm(r,f)，N(r,f),T(r,f),…,etc, and the classical results of R. Nevanlinna’s theory of meromorphic functions as found in [1, 2]. In particular, for a non-constant meromorphic functionf, we denote byS(r,f)any quantity satisfyingS(r,f)=o(T(r,f)) asr→+∞, possibly outside a set of valuerof finite linear measure. Throughout this paper, we denote by C the complex plane and byDa domain in C.

Letf，gbe non-constant meromorphic functions andcbe a finite complex number. We say thatfandgshare the valueciff-candg-chave the same zeros(see [2]).

In his inferential paper [3] on meromorphic functions and their derivatives,W.K.Hayman proved that iffis transcendental and meromorphic in C andnis an integer, thenfnf′ assumes every finite non-zero value infinitely often forn≥3 and that the same conclusion remains valid forn≥2 iffis entire.Hayman subsequently conjectured [4]that the same result still holds forn≥1 andftranscendental meromorphic. Since then,Hayman’s conjecture and its various versions have been studying by a lot of authors (see [5-15], etc). Finally, this Hayman conjecture was proved completely by W.Bergweiler and A.Eremenko [6],H.H.Chen and M.L.Fang [7],independently.

In 1993,C.C.Yang,L.Yang and Y.F.Wang[14] investigated an extended version of the above Hayman’s Conjecture and proved that iffis a transcendental entire function, andk,n(≥2) are positive integers, thenf(f(k))ntakes every finite non-zero value infinitely often. They also pointed out that the same conclusion holds forn=1 which is still open.

According to Bloch’s principle (see [17], p.222), it is natural to consider the normal family analogues of Haymam’s conjecture and Yang’s problem. In this direction,X.C.Pang and L.Zalcman,D.W.Meng and P.C.Hu proved the following results.

Inthispaper,westudythenormalityandsharedvalueformeromorphicfunctionsrelatedtoHayman’sconjectureandtheYang’sproblemandprovethefollowingresults.

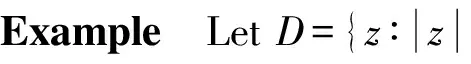
Theorem1.2 Let k≥2 be a positive integer and let f be a transcendental meromorphic function in C.If f has only zeros of multiplicity at least k and poles of multiplicity at least 3,then f f(k)assumes every finite non-zero complex number infinitely often.

2 Lemmas

Lemma2.2[13] Let k≥2 be a positive integer and let c be a non-zero constant. Suppose that f is a rational function but not a polynomial and that f has only zeros of multiplicity at least k and poles of multiplicity at least 2, then f f(k)-c has at least two distinct zeros.

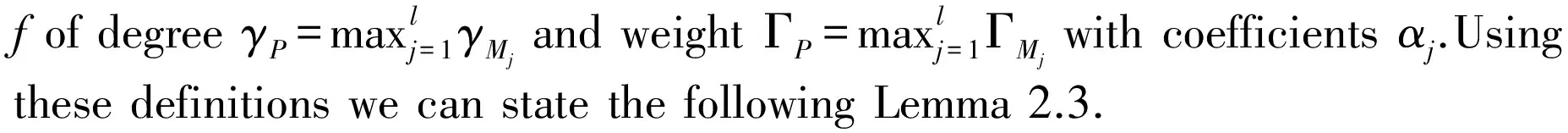
Lemma 2.3[19]Letfbeanon-constantmeromorphicfunctionandletQ1[f],Q2[f]bedifferentialpolynomialsinf.LetnbeapositiveintegerandfnQ1[f]=Q2[f].IfγQ2≤n,thenm(r,Q1[f])=S(r,f),whereγQ2isthedegreeofQ2[f].

3 Proof of Theorem 1.2

Letcbe a finite non-zero complex number.We write

(3.1)

By (3.1) we have

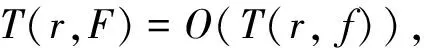
(3.2)

fφ=(-c)F′/F.

(3.3)

where

(3.4)

WeshallshowthatFisnotaconstant.Otherwisewehavef f(k)≡bforsomeconstantb.Sincefhasonlyzerosofmultiplicityatleastk,wefindb≠0andthusf≠0,whichmeansthatthefunctionb/f2mustbeentire.Thistogetherwiththefirstfundamentaltheoremyields

2T(r, f)+O(1)=T(r,b/f2)=

m(r,b/f2)=m(r, f(k)/f)=S(r, f),

sothatfisaconstant.Itisimpossible.

Nowwecanderivefrom(3.3)thatφ≢0.ByapplyingLemma2to(3.3)andnoting(3.2)weobtain

(3.5)

From(3.1)weseethatanypoleoffmustbeasimplepoleofF′/F,whichand(3.3)meansthatanypoleoffwithmultiplicitym(≥3)mustbeazeroofφwithmultiplicitym-1.Thuswehave

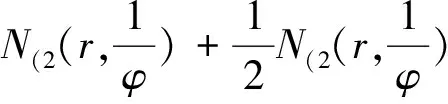
(3.6)

Ifz0is a zero offwith multiplicityn(≥k+1),then we see from (3.1) thatF′ has zeros atz0with multiplicity at leastnand,so isF′/Fsimply notingF(z0)=-c.From this and (3.3) it follows thatz0will never be a pole ofφ.Therefore,we deduce from (3.4) thatφcan only have poles at the zeros ofFand the zeros offwith multiplicity at mostk.This and (3.4) gives

(3.7)

From (3.2),(3.3) and the first fundamental theorem, we have

m(r, f)≤ m(r,1/φ)+S(r, f)=

T(r,φ)-N(r,1/φ)+S(r, f).

(3.8)

Sincefhas only poles with multiplicity at least 3, from (3.5)-(3.8)

T(r,f)=m(r,f)+N(3(r,f)≤T(r,φ)-

(3.9)

whichleadsto

Therefore,Fhas infinitely many zeros sincek≥2.Theorem 1.2 is proved.

4 Proof of Theorem 1.1

We first assert thatff(k)-chas at least two distinct zeros for every constantc≠0.

Suppose thatfis a polynomial.Thenff(k)is also a polynomial with degree at leastksincefhas only zeros of multiplicity at leastk,and thusff(k)-chas at least one zero.Ifff(k)-chas exactly one zero,sayz0,then there exist a non-zero constantλand a positive integermsuch thatff(k)=c+λ(z-z0)m,which,however,must have only simple zero sincec≠0 andm≥k.This is impossible becausefis a polynomial and all its zeros have multiplicity at leastk≥2.

We now suppose thatfis rational but not a polynomial,then our assertion follows from Lemma 2.2 immediately.Finally,iffis transcendental,then by Theorem 1.2 we know thatff(k)-cassumes zero infinitely often. So our assertion holds.

(4.1)

locally uniformly in C with respect to the spherical metric,wheregis a non-constant meromorphic function.By Hurwitz’s theorem,we see that all zeros ofghave multiplicity at leastkand all poles ofghave multiplicity at least 3.By (4.1) we get

(4.2)

spherically uniformly on every compact subset of C.

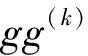
2T(r,g)+O(1)=T(r,c/g2)=

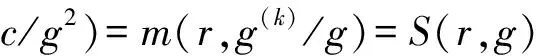
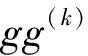
where

and

(4.3)

(4.4)

[1]HAYMAN W K.Meromorphic Functions [M].Oxford:Clarendon Press,1964.

[2]YANG C C,Yi H X.Uniqueness Theory Of Meromorphic Functions[M].Dordrecht,Beijing,New York:Kluwer Academic Publishers and Science Press,2003.

[3]HAYMAN W K.Picard values of meromorphic functions and their derivatives[J].Ann of Math,1959,70(1):9-42.

[4]HAYMAN W K.Research Problems In Function Theory[M].London:Athlone Press,1967.

[5]ALOTAIBI A.On the zeros of af(f(k))n-1 forn≥2[J].Comput.Methods Funct.Theory,2004,4(1):227-235.

[6]BERGWEILER W,EREMENKO A.On the singularities of the inverse to a meromorphic function of finite order[J].Rev Mat Iberoamericana,1995,11(2):355-373.

[7]CHEN H H,FANG M L.On the value distribution offnf′[J].Sci China,Ser A,1995,38(7):789-798.

[8]CLUNIE J.On a result of Hayman[J].J London Math Soc,1967,42(1):389-392.

[9]JIANG Y.A note on the value distribution off2(f′)nforn≥2[J].Bull Korean Math Soc,2016,53(2):365-371.

[10]MUES E.Uber ein problem von Hayman[J].Math Z,1979,164(3):239-259.

[11]PANG X C,ZALCMAN L.On theorems of Hayman and Clunie[J].New Zealand J Math,1999,28(1):71-75.

[12]WANG J P.On the zeros offn(z)f(k)(z)-c(z)[J].Complex Var Elliptic Equ,2003,48(8):695-703.

[13]WANG J P.Normal family of meromorphic functions[J].Bull Korean Math Soc,2014,51(3):691-700.

[14]YANG C C, YANG L, WANG Y F.On the zeros off(f(k))n-a[J].Chin Sci Bull,1993,38(24):2125-2128.[15]YANG P,QIAO L.Derivatives of meromorphic functions and polynomial functions[J].Complex Var Elliptic Equ,2016,61(6):791-802.

[16]SCHIFF J L.Normal Families[M].New York, Berlin,Heidelberg:Springer,1993.

[17]ZALCMAN L.Normal families:New perspectives[J].Bull Amer Math Soc(N.S.),1998,35(3):215-230.

[18]MENG D W,HU P C.Normality criteria of meromorphic functions[J].J Math Anal Appl,2011,381(2):724-731.

[19]DOERINGER W.Exceptional values of diffieretial polynomials[J].Pacific J of Math,1982,98(1):55-62.

(责任编辑 邓 颖)

涉及海曼猜测的正规定则

王建平

(绍兴文理学院 数理信息学院，浙江 绍兴312000)

研究涉及海曼猜测的亚纯函数的正规性和分担值，证明了一个正规定则，改进了庞学诚，Zalcman等人的结果.

正规族;分担值;亚纯函数;Nevanlinna 理论

Foundation item:This work was supported by the National Natural Science Foundation of China(No.11401387,No.11501374) and the Natural Science Foundation of Zhejiang Province,China(No.LQ14A010007, No.LQ14A010006)

10.16169/j.issn.1008-293x.k.2016.09.05

Received date: 2016-08-15

Biography:Wang Jianping(1958- ),Male;Born in Shaoxing,Zhejiang,Ph.D.,Professor;Research field is complex analysis.