埋深对压气储能内衬洞室稳定性影响的定量分析

夏才初 赵海斌 梅松华 周舒威 张平阳 周 瑜

(1.绍兴文理学院 土木工程学院，浙江 绍兴312000；2.同济大学 隧道及地下建筑工程系，上海 200092；3.中国电建集团中南勘测设计研究院有限公司 水能资源利用关键技术湖南省重点实验室，湖南 长沙410014)

埋深对压气储能内衬洞室稳定性影响的定量分析

夏才初1,2赵海斌3梅松华3周舒威2张平阳2周 瑜2

(1.绍兴文理学院 土木工程学院，浙江 绍兴312000；2.同济大学 隧道及地下建筑工程系，上海 200092；3.中国电建集团中南勘测设计研究院有限公司 水能资源利用关键技术湖南省重点实验室，湖南 长沙410014)

采用热力耦合数值模型定量分析埋深对压气储能内衬洞室稳定性的影响.通过建立洞室内空气能量和质量守恒方程、洞室传热控制方程以及热弹性受力变形控制方程，从而建立压气储能内衬洞室热力耦合计算模型.对不同埋深时的压气储能洞室其受力变形特征进行模拟，对一个周期内的应力及变形进行分析，获得了不同埋深对压气储能内衬洞室稳定性的影响.数值模拟结果表明：埋深对密封层第一主应力和第三主应力影响不大.埋深越大，衬砌拉应力越小，而压应力越大；埋深只影响衬砌一个周期内前几个小时以及后几个小时的第三主应力值，对其余阶段应力影响不大.埋深越大，围岩压应力越大，第一主应力波动幅度越小；埋深增加，第三主应力增加.埋深越大，水平位移越小.每个时间节点洞顶竖向位移均随埋深的增加而减小.

压气储能：内衬洞室；第一主应力；第三主应力；环向应变；洞壁位移

0 引言

压气空气储能CAES(Compressed Air Energy Storage)是一种利用压缩空气作为介质来储存能量和发电的技术[1].压气储能系统蓄能时利用风能等富余的电量驱动压气机将空气压缩并储存在储气库中；发电时，释放储气室的压缩空气，将压缩后的高压空气送入燃烧室与喷入的燃料混合燃烧产生高温、高压燃气，进入燃气透平机中膨胀做功，带动发电机发电，供电网使用.迄今，世界上仅建成了两座商业化运行的压气储能电站，即1978年建成的德国Huntorf电站(290 MW)[1]和1991年建成的美国阿拉巴马McIntosh电站(110 MW)[2].此外，美国多个州[3-4]、日本[5]、以色列[6-7]、韩国[8]等国正在建设和计划建设以岩盐溶腔、地下含水层、岩石内衬洞室为地下储气构造物的压气储能电站.

作为压缩空气储能电站主要组成部分，地下储气构造物是压气蓄能电站选址的决定因素，也是其运行性能和可靠性的技术关键.压气储能电站地下洞室的规模大(数十万m3到数千万m3)、空气压力高(5～10 MPa或更大)、密封性要求严(24 h泄漏率不大于1.0%～0.5%)，而且压气储能电站在储能和发电过程中，压缩空气是反复循环作用在洞室内壁.因此，压气储能电站建设中急需解决高内部气压下地下洞室围岩稳定性这一基本问题.

这个问题可以借助计算机的强大运算能力，运用数值模拟进行深入探讨.对此，Allen等[9]采用有限元法，考虑了洞室尺寸、间距和侧压力系数对开挖后压气储能洞室围岩塑性区的影响.Zimmels等[7]用FLAC针对侧压力系数0.75、衬砌厚度1m的压气储能圆形洞室的围岩塑性区进行计算，分析了埋深、开挖半径、内压、洞室间距等因素对洞室稳定性的影响.但这些模拟尚没有考虑热力效应，进一步的数值模拟应充分考虑该效应.

我国目前正在西北以及华中地区进行压气储能内衬洞室选址工作，这要求对影响稳定性的各种敏感因素进行深入细致的分析.洞室埋深作为一个基本的因素，目前尚未有埋深对压气储能内衬洞室稳定性影响的细致报道.因此，本文通过建立热力耦合数值模型，对不同埋深下的洞室受力变形情况进行定量分析.

1 数值模型的建立

1.1 压气储能洞室内压及温度场控制方程

为了计算方便，本文采用了一种压气储能的概念模型，略去与天然气储库类似的构造(如排水区和滑动层等)，只关注与稳定性密切相关的部分，最终考虑洞室稳定系统由密封层、衬砌和围岩组成(如图1).

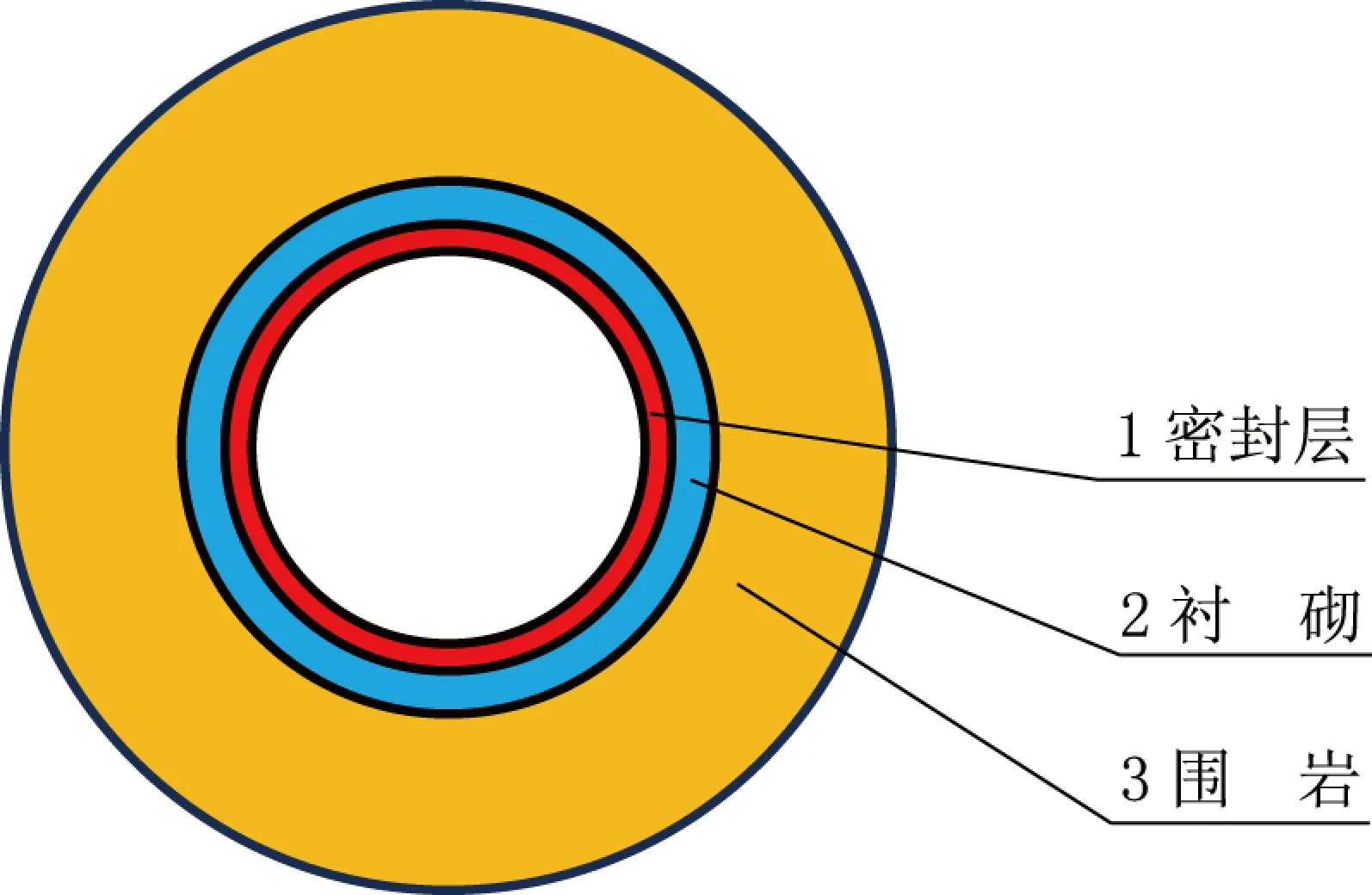
图1 传热模型示意图

对于岩石内衬洞室，在密封层、衬砌和围岩内，满足传热控制方程：

(1)

式中：ρj、cpj、kj和Tj分别为第j层介质的密度、比定压热容、导热系数和温度，同时j=1,2,3分别代表密封层、衬砌和围岩；rj-1和rj分别为第j层介质的内边界半径和外边界半径.

式(1)的边界条件：

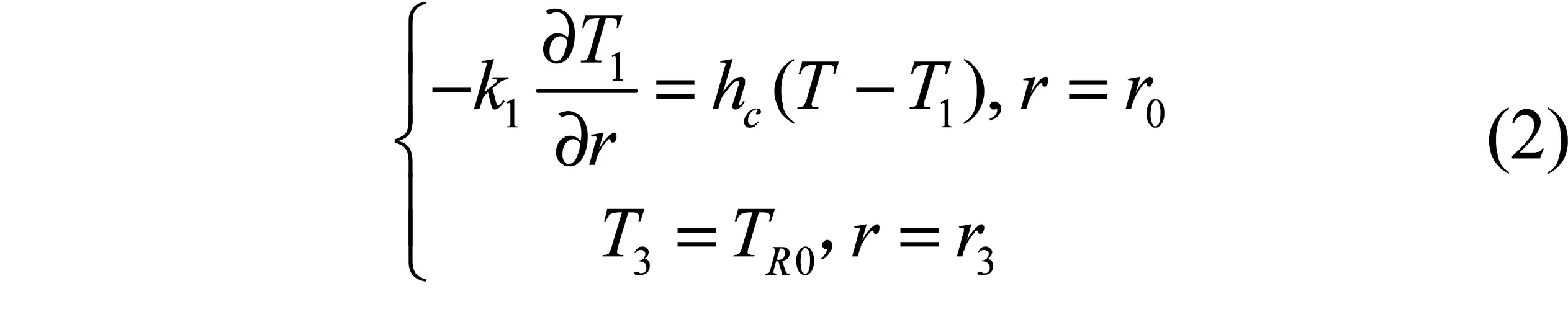
式中：T为洞室内空气温度，hc是密封层与空气的平均传热系数，TR0为围岩外部恒温层温度.

式(1)需要的连续性条件有：

(3)

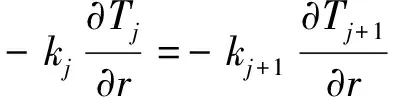
(4)

在进行洞室内气体抽放循环前，密封层、衬砌和围岩内的温度相等，在压气储能开始工作时的温度初始条件如下：

(5)

由式(2)可知，要求解密封层、衬砌以及围岩的温度，必须知道洞室内的气体温度变化情况，因此需建立洞室内气体温度的数学求解模型.由于密封层的密封性以及衬砌的低渗透率，洞室内气体泄露对气压以及温度的影响可以忽略不计.以温度、密度作为气体状态变量，由洞室内气体的质量守恒可以得到[10]：

(6)

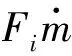
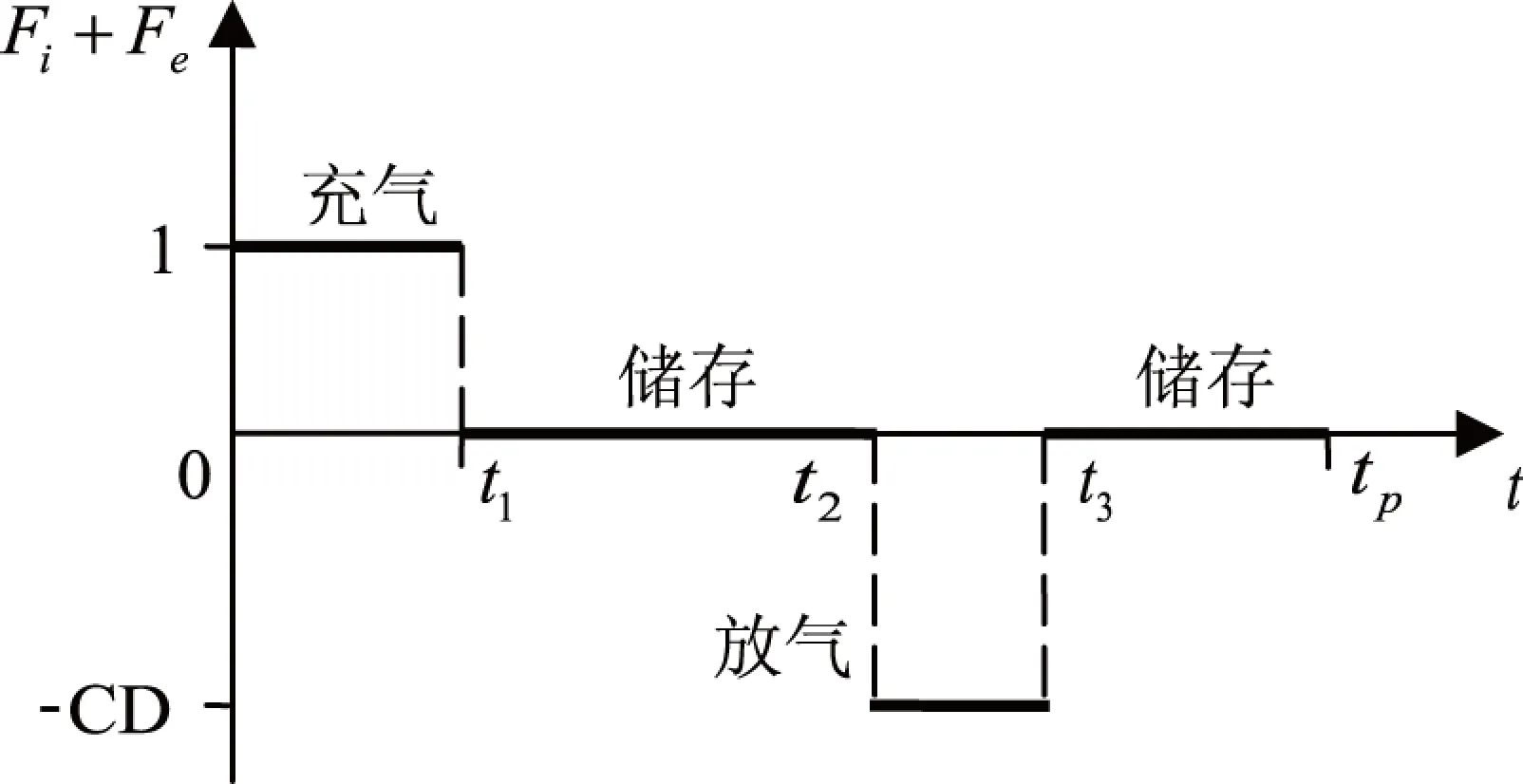
图2 Fi+Fe在一个典型的压气储能循环中的变化

1.2 压气储能内衬洞室热力耦合数值模型

根据传统CORDIC算法的原理，把初始相位角转换到[0,π/4]范围内，则可以跳过n=0级的迭代.设初始向量经过CORDIC算法N次迭代后，此时向量的坐标为(XN,YN)，则幅度可表示为相位可表示为θ=ZN+arctan(YN/XN).因此，可定义幅度修正因子剩余未旋转角度Δθ=arctan(YN/XN).由于剩余未旋转角度可表示为易知其最大值为：

压气储能洞室运营期间，洞室周围衬砌以及围岩的应力场由洞室开挖形成的初始应力场和洞室内高压气体以及温度场变化引起的应力场组成.因此采用COMSOL软件进行模拟，建立高内压和温度反复耦合作用下压气储能内衬洞室热力耦合数值模型.首先，为了对数值模型进行验证，采用某一洞室初步设计尺寸(r0=8.0 m,r1=8.1 m，V=3×105m3)及典型的洞室断面进行建模.图3给出了模型的网格布置，其中洞室由密封层、混凝土衬砌以及围岩组成.同时该图还给出了详细的洞室尺寸，模型的上下边界以及右边界到洞室内表面的距离为6r0，整个模型总共包含15 221个二次离散的三角形单元.

在对模型进行离散后，进行压气储能内衬洞室温度场和应力场的求解，主要过程如下：

1)建立固体力学模块，得到初始地应力场，该模块的边界条件以及荷载条件如图3所示，控制方程为弹性力学基本方程；

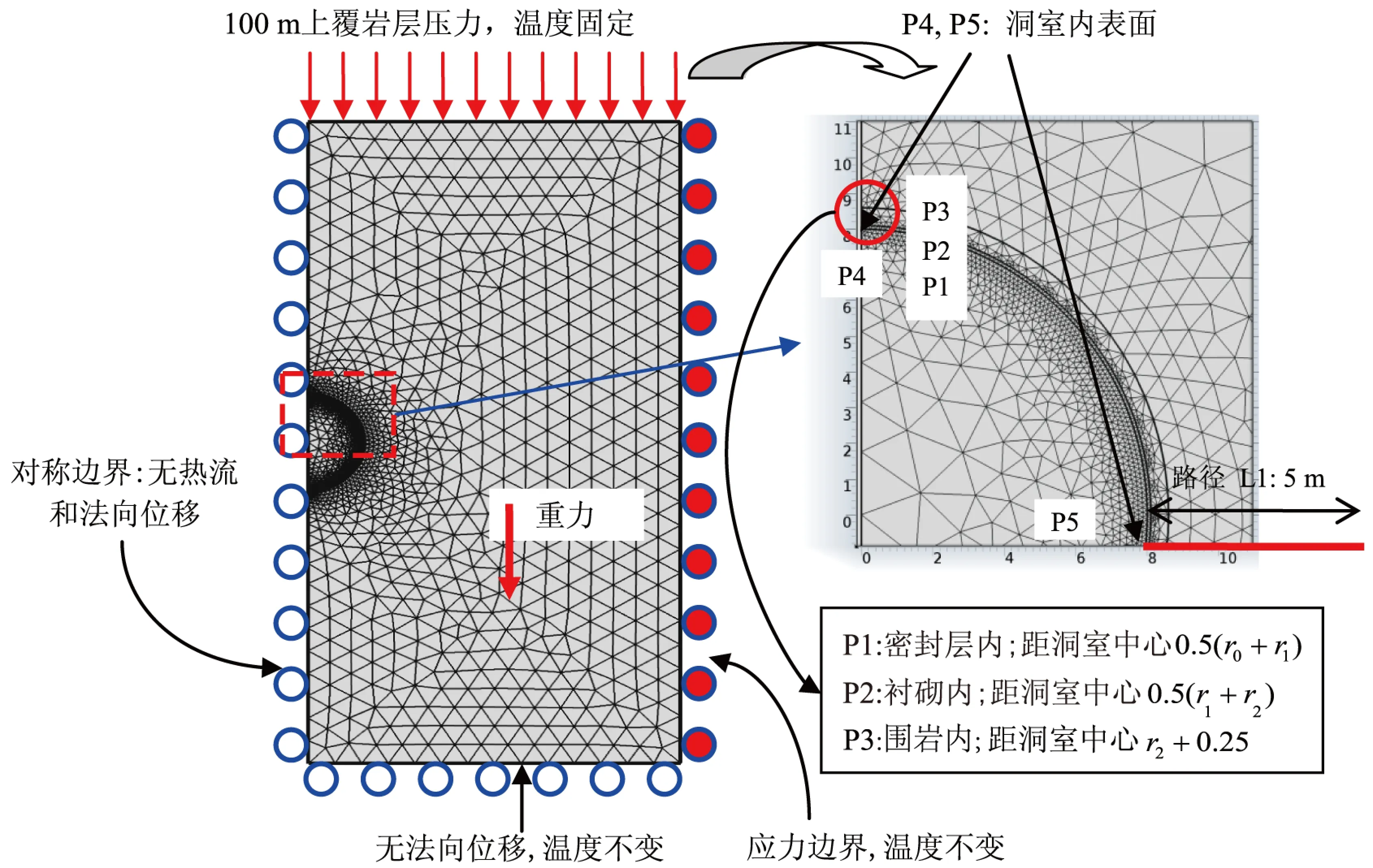
图3 模型网格和边界条件

2)求解洞内气体状态,将其作为一个独立的模块，该模块囊括了洞室内气体温度、压强和密度求解所需的所有控制方程；

3)建立由密封层、衬砌和围岩组成的传热模块和热弹性模块；

4)洞内气体与传热模块、热弹性模块、初始地应力模块之间的关系如图4所示.4个模块之间进行耦合求解；

5)设定好计算时间以及初始状态，然后进行计算.

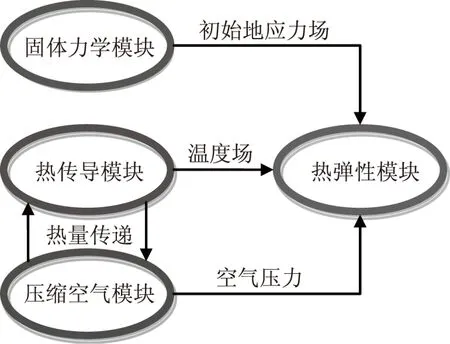
图4 模块之间的相互关系

2 埋深对第一主应力的影响

图5 不同埋深时充气后第一主应力

图6为不同埋深时密封层、衬砌以及围岩第一主应力变化情况.从图6可以看出，埋深对密封层第一主应力影响不大；埋深增加对衬砌的受力情况有较大的影响，埋深越大，拉应力越小,而压应力越大；同时,埋深越大，围岩压应力越大，第一主应力的波动幅度越小.

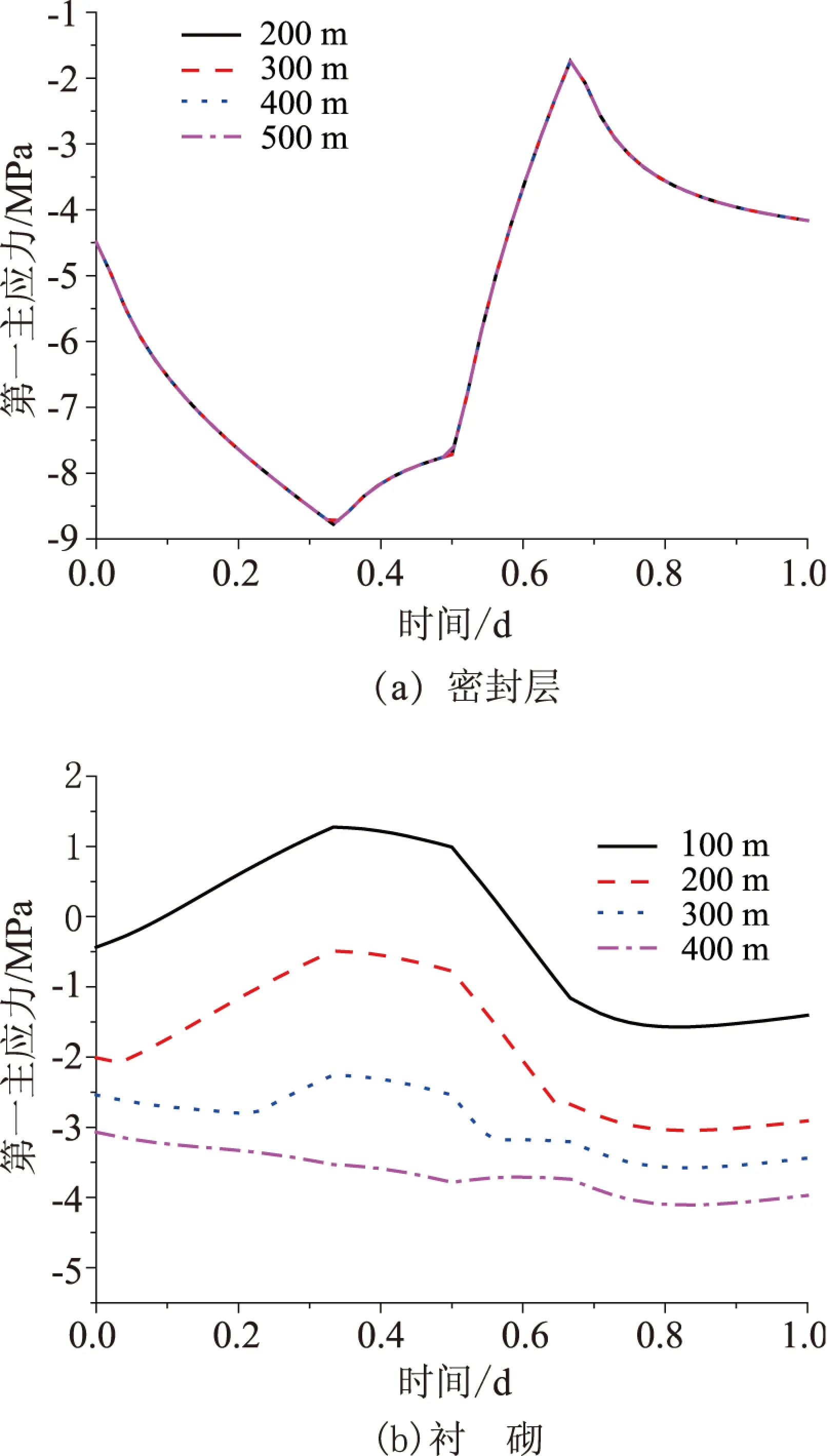
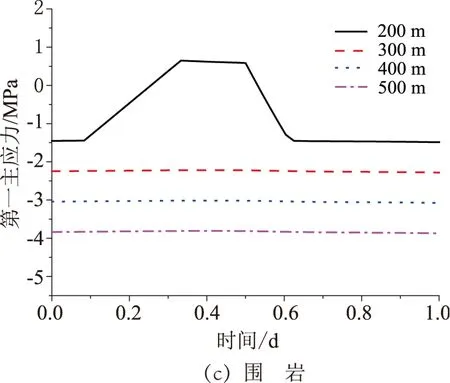
图6 不同埋深时一个周期内第一主应力

3 埋深对第三主应力的影响

图7给出了不同埋深时洞室周围的第三主应力情况，从中可以看出，埋深对洞周第三主应力的最大值和最小值影响很小.

图8、图9和图10分别为不同埋深时密封层、衬砌和围岩的第三主应力变化情况.从图8可看出，埋深对密封层第三主应力几乎没有影响.

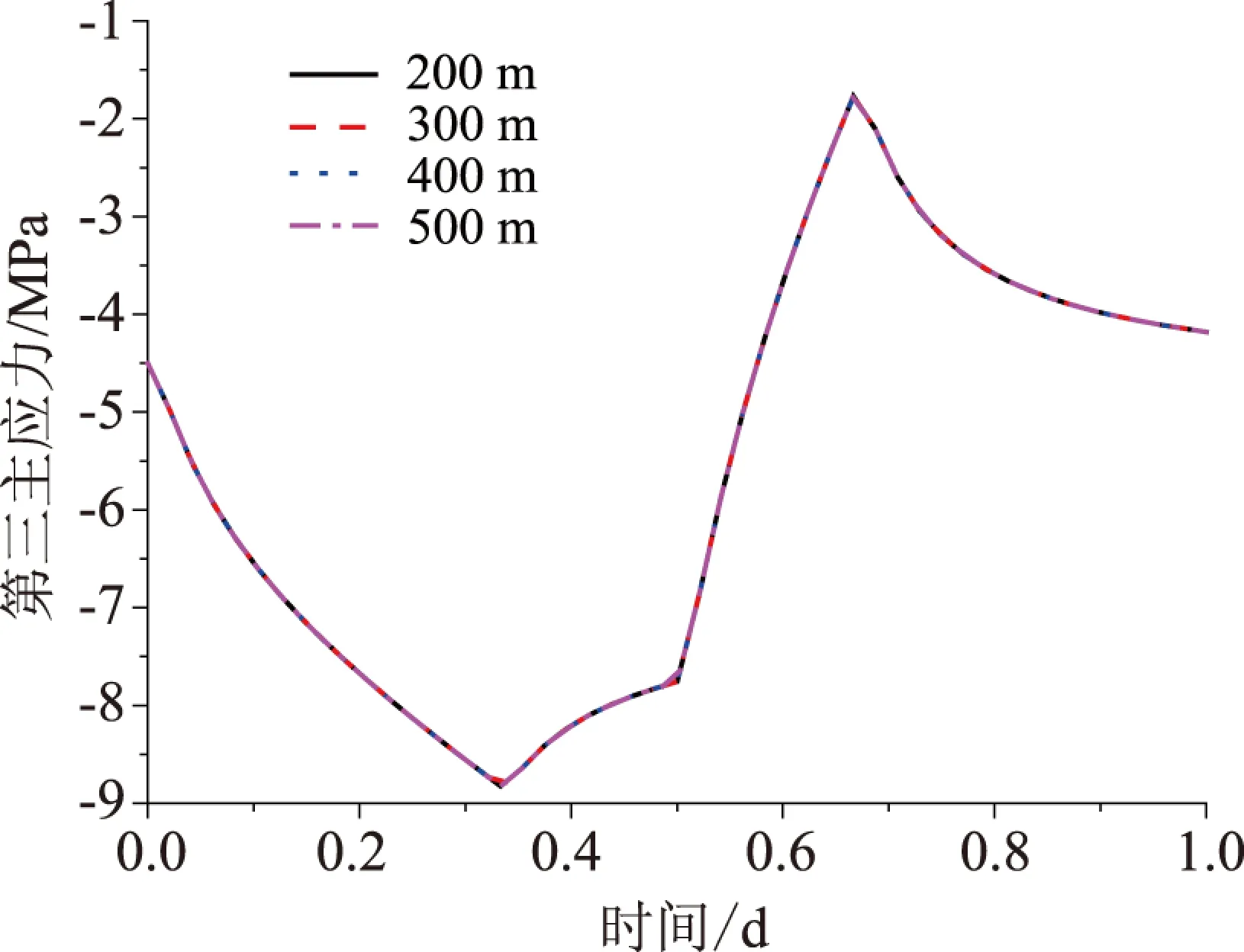
图8 不同埋深时一个周期内密封层第三主应力

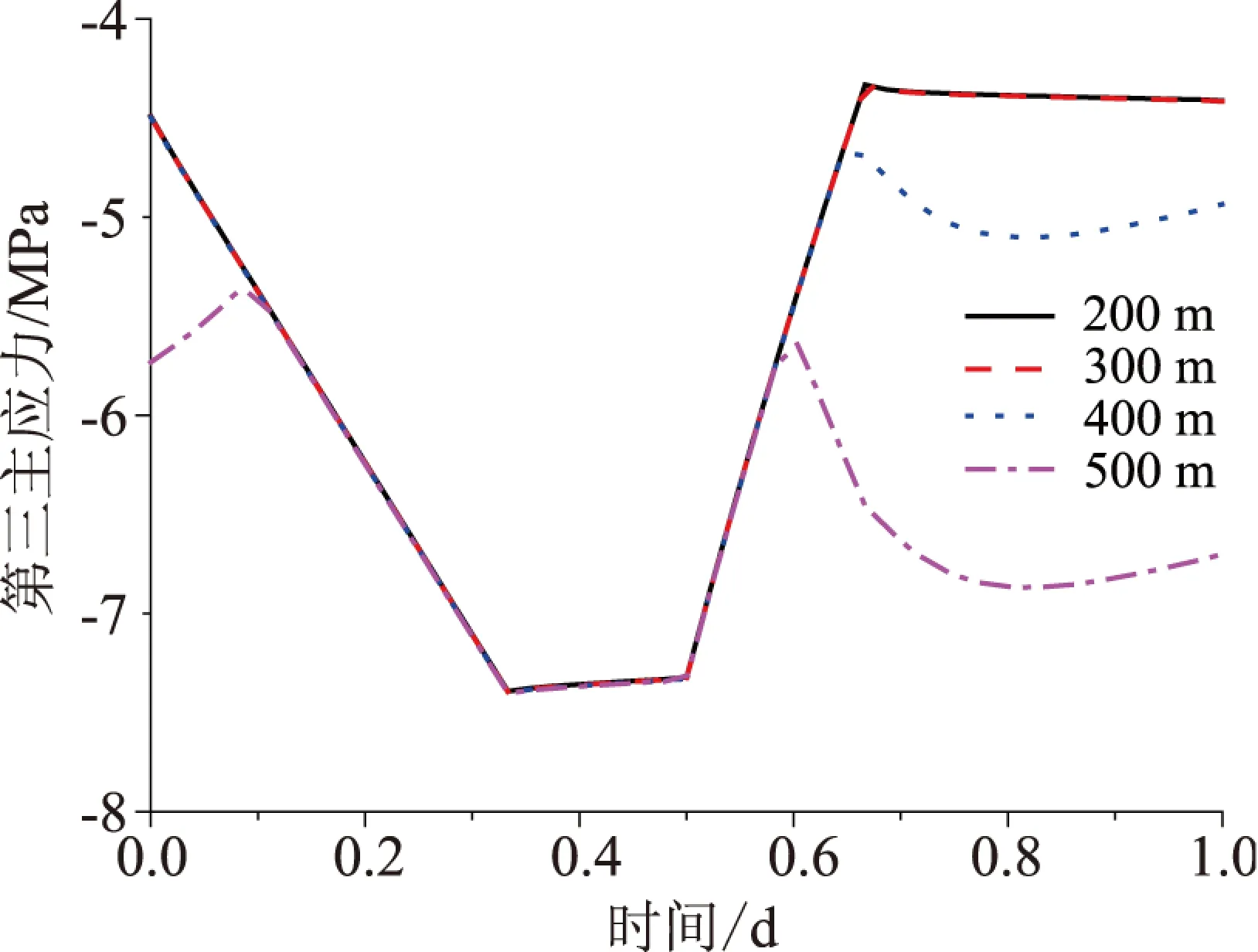
图9 不同埋深时一个周期内衬砌第三主应力

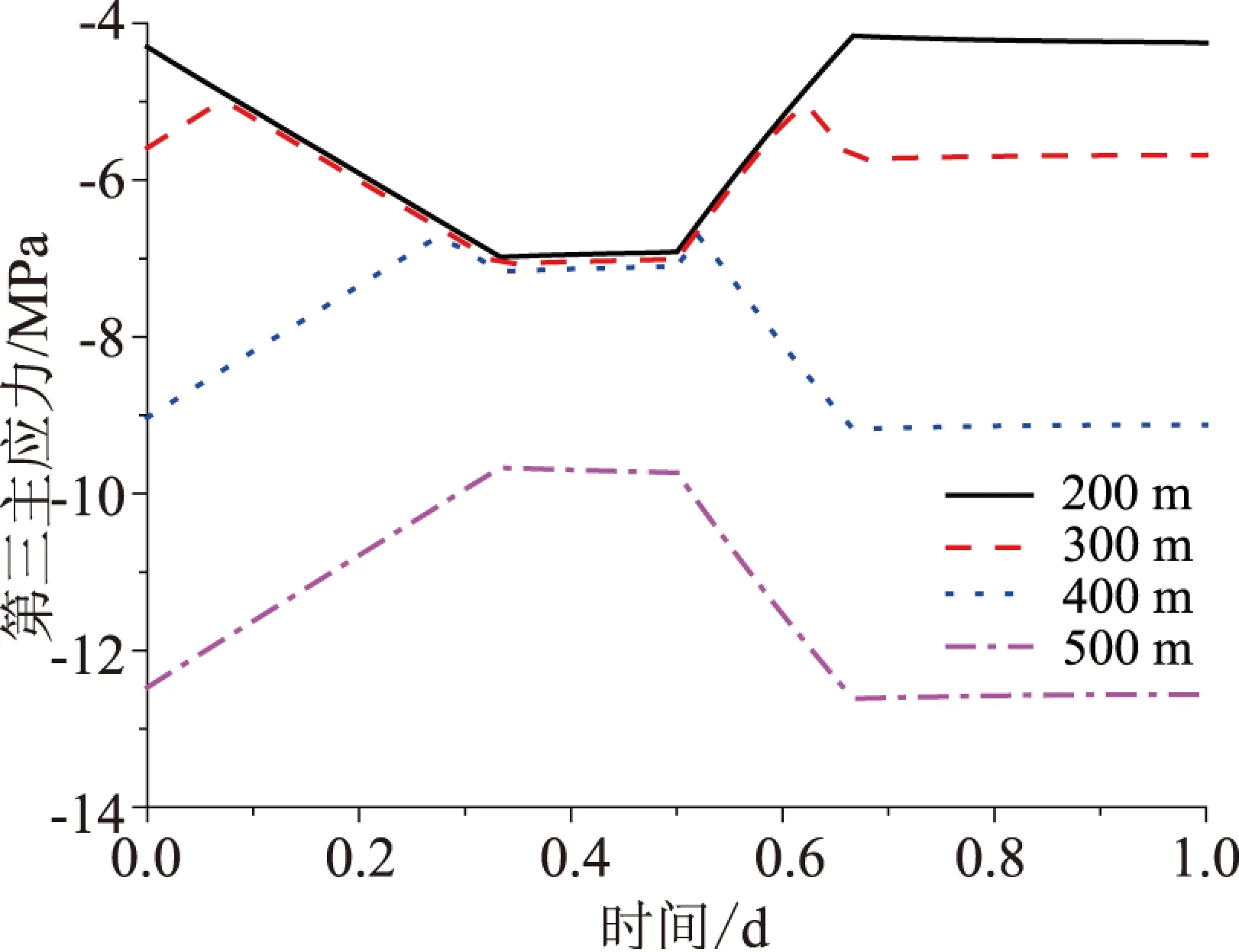
图10 不同埋深时一个周期内围岩第三主应力

从图9可以看出，埋深只影响衬砌一个周期内前几个小时以及后几个小时的第三主应力值，对其余阶段应力影响不大.从图10围岩内表面第三主应力变化情况可以看出，埋深增加时第三主应力的变化趋势发生改变，埋深200 m时一个周期内为“上升—下降—上升—下降”(应力绝对值)；而埋深为400 m和500 m时，围岩应力变化为“下降—上升—上升—平稳”.总体而言，埋深增加，第三主应力增加.

4 埋深对环向应变的影响

图11为衬砌内表面环向应变变化情况.由图11可见，衬砌环向受拉，拉应变经历“上升—下降—下降—上升”过程.埋深变化时衬砌环向应变变化很大，埋深增加时衬砌的环向应变减小.

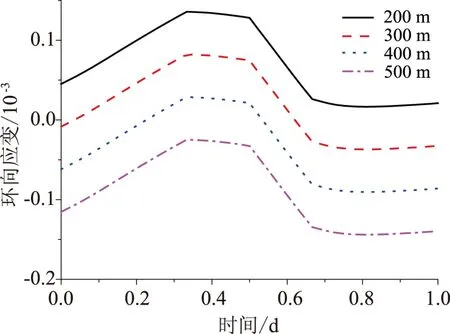
图11 不同埋深时一个周期内衬砌环向应变

围岩内表面环向应变变化情况如图12所示.由图12可见，围岩环向应变规律与衬砌一致：埋深增加时，围岩环向应变减小.

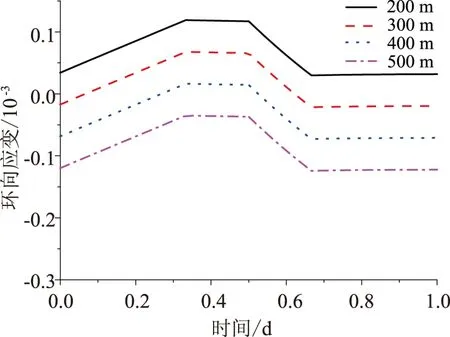
图12 不同埋深时一个周期内围岩环向应变

5 埋深对洞壁位移的影响

图13给出了不同埋深时洞室周围水平位移情况.由图13可见，埋深分别为200 m、300 m、400 m和500 m时，水平位移最大值分别为2.19 mm、1.66 mm、1.19 mm和0.73 mm.埋深越大，水平位移越小.

图14给出了不同埋深时洞室周围竖向位移情况.由图14可见，当埋深为200 m、300 m、400 m和500 m时，竖向位移最大值分别为1.45 mm、0.81 mm、1.53 mm和2.25 mm.

图13 不同埋深时充气后水平位移

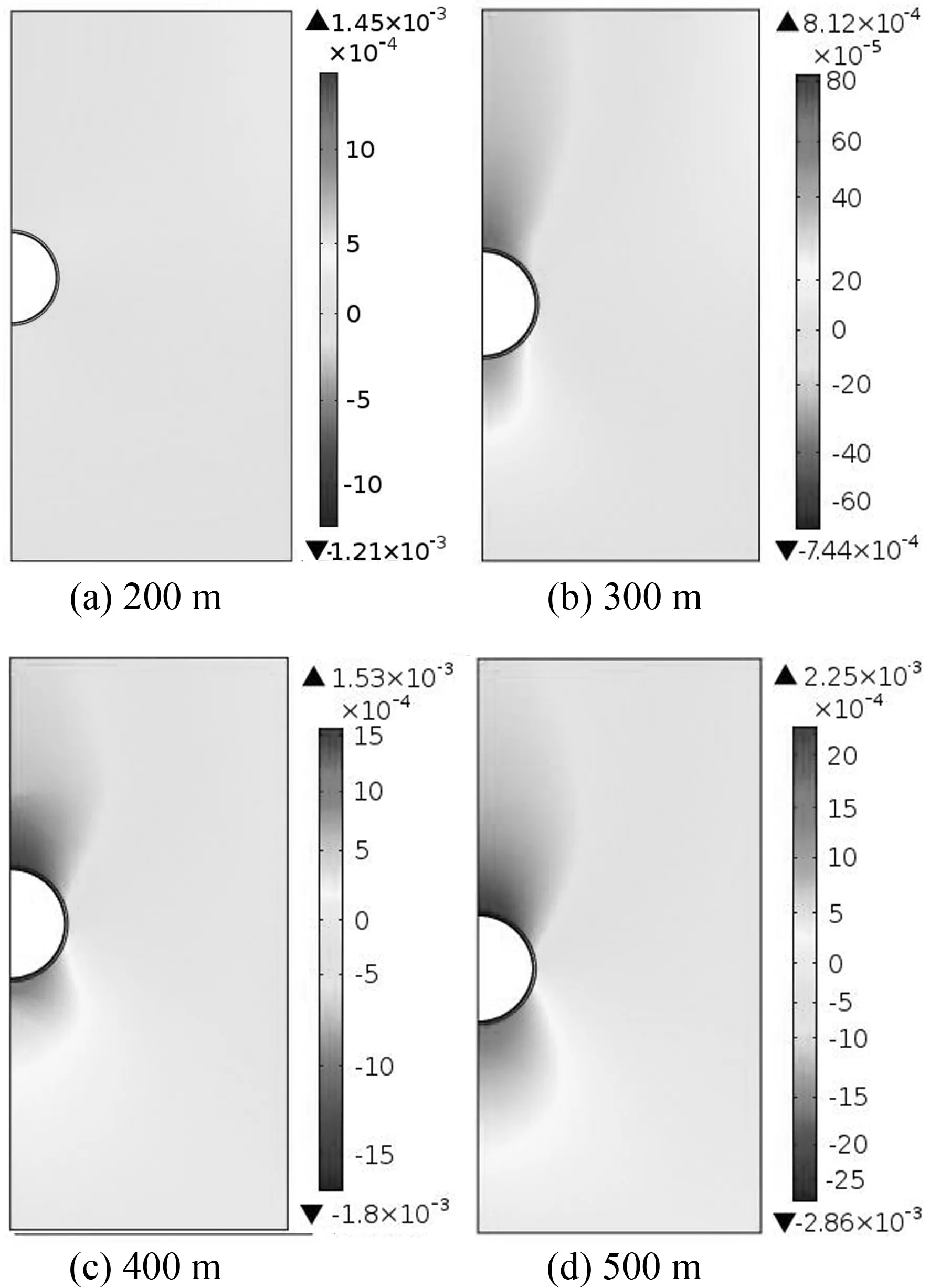
图14 不同埋深时充气后竖向位移

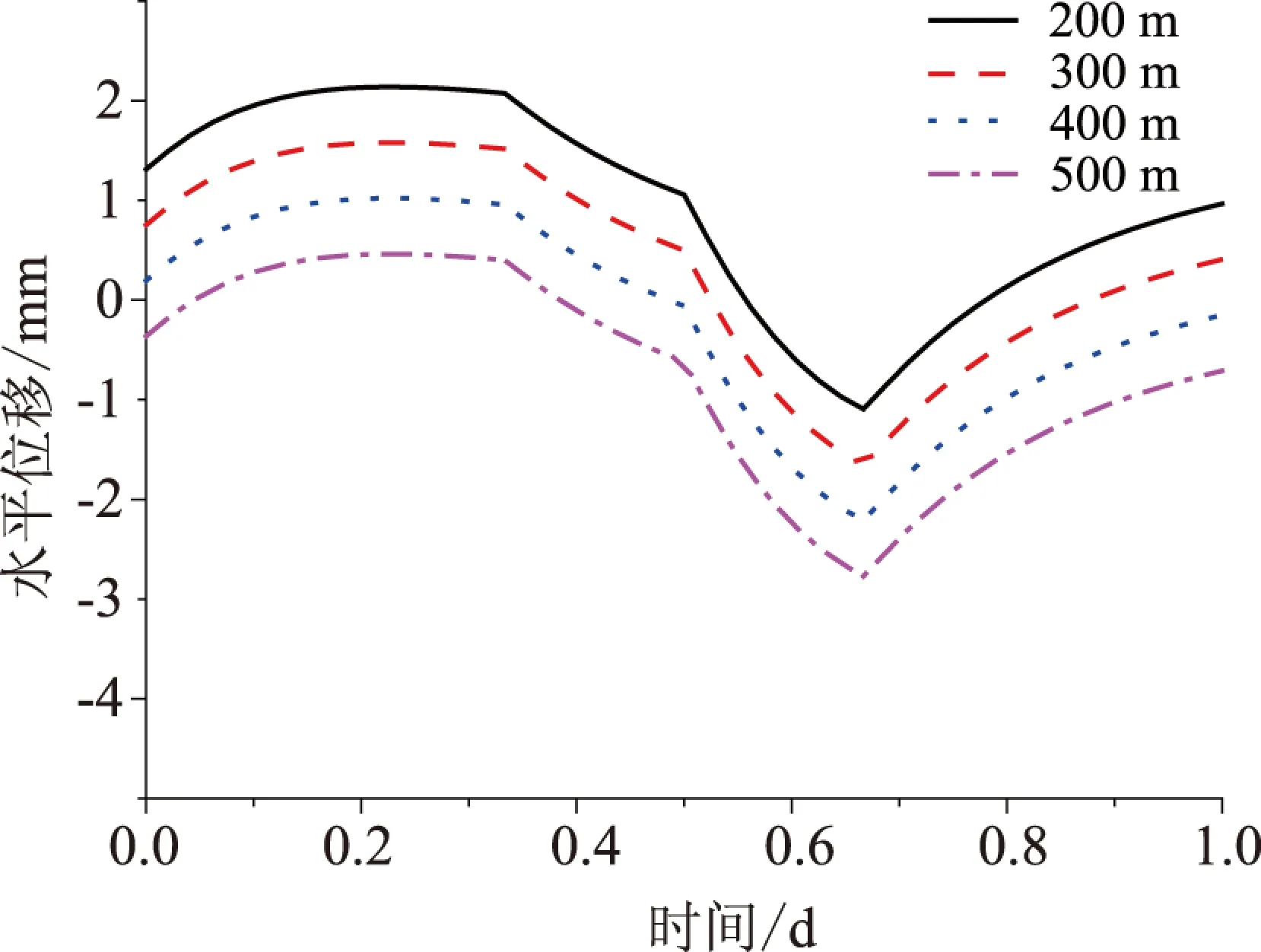
图15 不同埋深时一个周期内洞侧水平位移

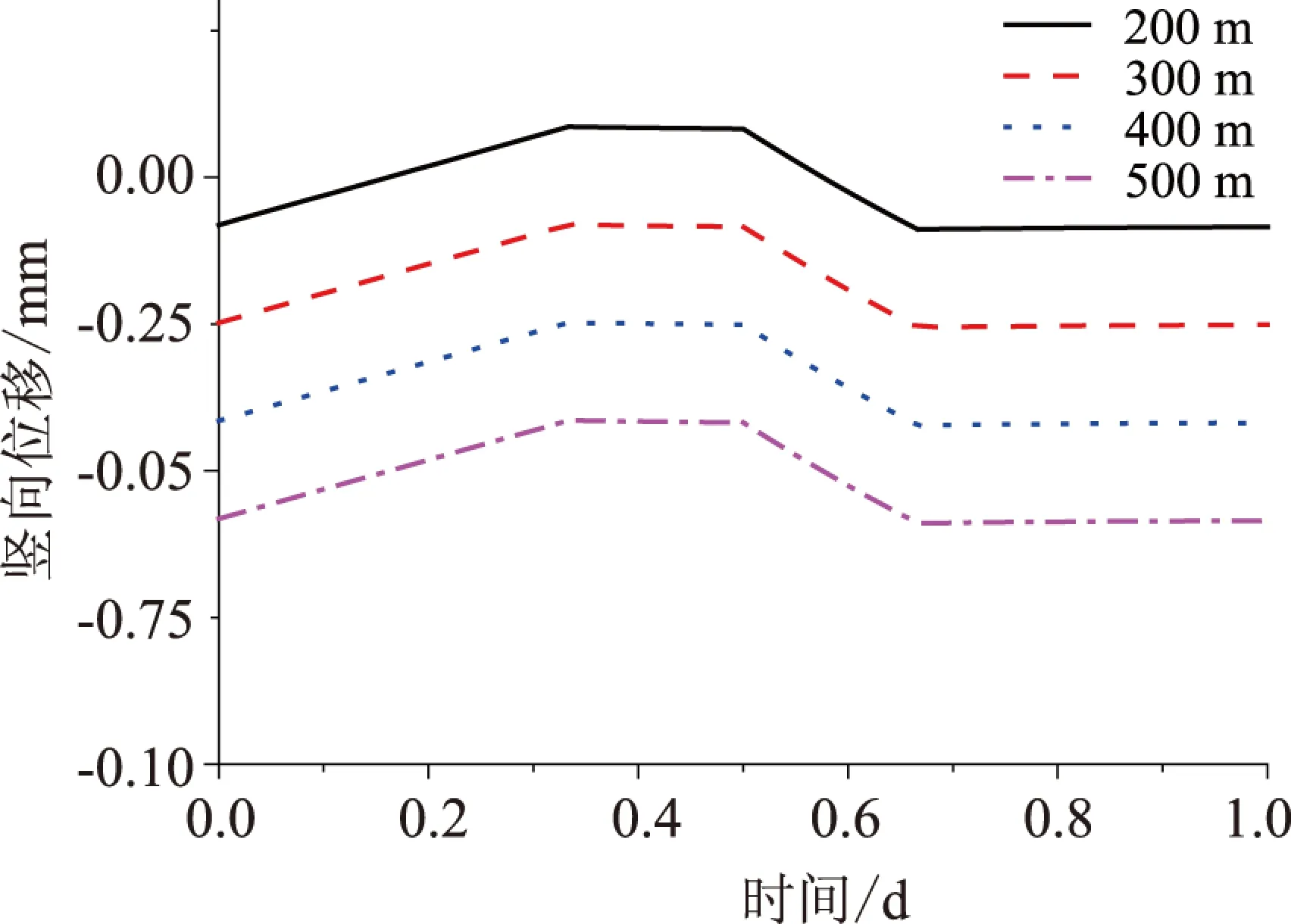
图16 不同埋深时一个周期内洞顶竖向位移

图15给出了不同埋深时洞侧水平位移的变化情况.从图15可以看出，埋深减少时洞侧水平位移增大.

图16为洞顶竖向位移变化情况.从图16可以看出，在每个时间节点，洞顶竖向位移均随埋深的增加而减小.

6 结论

通过洞室内空气能量和质量守恒方程、洞室传热控制方程以及热弹性受力变形控制方程，建立了压气储能内衬洞室热力耦合计算模型，对不同埋深时压气储能洞室的受力变形特征进行模拟，对一个周期内的应力及变形进行分析，获得不同埋深对稳定性的影响.主要结论有：

1)埋深对密封层第一主应力和第三主应力影响不大.

2)埋深越大，衬砌拉应力越小而压应力越大.埋深只影响衬砌一个周期内前几个小时以及后几个小时的第三主应力值，对其余阶段应力影响不大.

3)埋深越大，围岩压应力越大，第一主应力波动幅度越小.埋深增加，第三主应力增加.

4)埋深越大，水平位移越小.每个时间节点洞顶竖向位移均随埋深的增加而减小.

[1]CROTOGINO F,MOHMEYER K U,SCHARF R.Huntorf CAES:More than 20 years of successful operation[J].Orlando,Florida,USA,2001.

[2]DAVIS L,SCHAINKER R.Compressed air energy storage (CAES):Alabama electric cooperative Mcintosh plant-overview and operational history[C]//Electricity storage association meeting:energy storage in action,Knoxville,TN.2006.

[3]SCHULTE R H,CRITELLIJR N,HOLST K,et al.Lessons from Iowa:development of a 270 megawatt compressed air energy storage project in Midwest independent system operator[J].Sandia National Laboratories,Albuquerque,2012.

[4]SUCCAR S,WILLIAMS R H.Compressed air energy storage:theory,resources,and applications for wind power[R].Princeton:Princeton Environmental Institute,2008.

[5]HAYASHI M.Rock mechanics of compressed air energy storage and super magnetic energy storage in Japan[C]//Rock Mechanics in Japan,1991,Vol.6,pp.50-57.Tokyo:Japanese Committee for ISRM,1991.

[6]KUSHNIR R,DAYAN A,ULLMANN A.Temperature and pressure variations within compressed air energy storage caverns[J].International Journal of Heat and Mass Transfer,2012,55(21-22):5616-5630.

[7]ZIMMELS Y,KIRZHNER F,KRASOVITSKI B.Design criteria for compressed air storage in hard rock[J].Energy &Environment, 2009,13(6):851-872.

[8]SONG W K,RYU D W,LEE Y K.Stability analysis of concrete plugs in a pilot cavern for compressed air energy storage[C]//12th ISRM Congress.International Society for Rock Mechanics,2011.

[9]ALLEN R D,DOHERTY T J,FOSSUM A F.Geotechnical issues and guidelines for storage of compressed air in excavated hard rock caverns[J].NASA STI/Recon Technical Report N,1982,82:33872.

[10]ZHOU S W,XIA C C,DU S G,et al.An analytical solution for mechanical responses induced by temperature and air pressure in alined rock cavern for underground compressed air energy storage [J].Rock Mechanics and Rock Engineering,2015,48(2):749-770.

(责任编辑 邓 颖)

Quantitative Analysis of Impact of Cover Depth on Stability of a Lined Rock Cavern for Compressed Air Energy Storage

Xia Caichu1,2Zhao Haibin3Mei Songhua2Zhou Shuwei2Zhang Pingyang2Zhou Yu2

(1.School of Civil Engineering, Shaoxing University, Shaoxing, Zhejiang 312000;2. Department of Geotechnical Engineering, Tongji University, Shanghai 200092;3. Hunan Provincial Key Laboratory of Key Technology on Hydropower Development,Hydro China Zhongnan Engineering Corporation, Changsha, Hunan 410014)

An quantitative analysis of the impact of cover depth on the stability of a lined rock cavern for compressed air energy storage (CAES) was made using the coupling thermo-mechanical numerical simulation. The mass and energy conservation for air in the cavern, governing equations for heat transfer and thermo-elastic loading and deformation were set up, which were coupled to constitute the model for compressed air energy storage in a lined rock cavern. The stress and deformation characteristics of the lined rock cavern for CAES under different cover depths were simulated and stress and deformation in a typical cycle were analyzed to take the effect of depth into account. The numerical simulation shows that the cover depth has a negligible effect on the first and third principal stresses of sealing layer. Lager cover depths result in a lager compressed stress and a smaller tensile stress in the concrete. The depth just affects the third principal stress in the first few hours and the last few hours in one cycle for the concrete, however, it affects the stresses less at other stages. A lager cover depth causes a larger compressive stress and smaller amplitude of first stress for the rock. In addition, the third principal stress for rock increases with the increase in depth. The vertical displacement at the top of the cavern at each time node decreases when the cover depth increases.

compressed air energy storage; lined rock cavern; first principal stress; third principal stress; hoop strain; displacement of the cavern wall

2016-11-07

夏才初(1963- )，男，浙江杭州人，博士，教授，研究方向：岩石力学、隧道与地下建筑工程.

10.16169/j.issn.1008-293x.k.2016.09.01

TU93

A

1008-293X(2016)09-0001-07