静电场求解的三种方法研究

郭福强 张保花 王俊珺

（昌吉学院物理系 新疆 昌吉 831100）

静电场求解的三种方法研究

郭福强 张保花 王俊珺

（昌吉学院物理系 新疆 昌吉 831100）

本文从实际静电问题出发，利用静电场基本特点以及静电场满足的微分表达式、几种不同类型边值条件下的边值关系，从中总结规律，提出比较简单的求解静电场问题的三种方法，即分离变量法、镜像法、格林函数法，分析三种方法求解静电场的基本原理、步骤和特点，使其学生更好地应用方法解决实际问题，并且通过研究可以使学生获得本领域内分析和处理一些基本静电问题的初步能力。

静电场分离变量法镜像法格林函数法

1 引言

静电场问题是《电磁学》和《电动力学》所研究的关键问题，在《电磁学》中，求解静电场问题大多是利用高斯定理求解静电场，而在实际生活和生产中高度对称性的问题很少，而是更加一般的静电问题，很难利用高斯定理求解。那么，通过《电动力学》的学习，提出了求解一般情况下静电场的三种方法：分离变量法、镜像法、格林函数法，本文通过对这三种方法的介绍，比较这些方法的特点和适用条件，为后期学生学习静电场的求解提供指导，并能利用这些方法解决一些更为实际的静电问题。

2 静电场的特点

静电场是静止的电荷所产生的场，它具有以下特点：

对于非均匀介质而言，介质内部存在束缚电荷ρp。

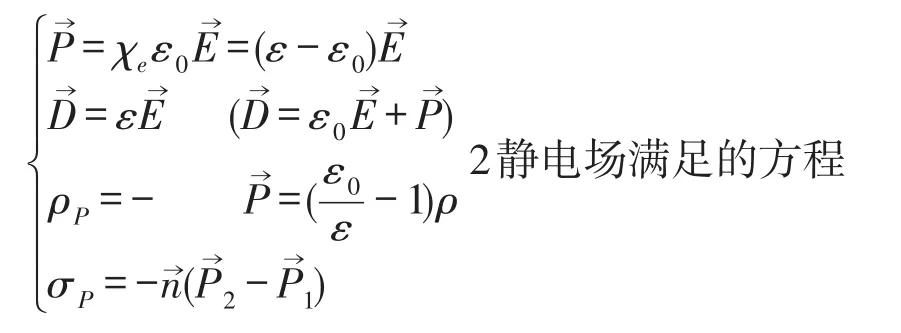
（1）均匀各向同性线性介质[1]：

（2）静电平衡时的导体：

3 求解静电场问题的三种方法

3.1 分离变量法

3.1.1 基本原理

在许多实际问题中，静电场是有带电导体决定的。例如，电容器内部的电场是由作为电极的两个导体板上所带电荷决定的[2]。而这些问题的特点是：空间中没有自由电荷分布，而自由电荷只出现在一些导体的表面上，因此，如果选择这些导体表面作为区域V的边界，则在V内部自由电荷密度ρ=0，因而泊松方程化简为比较简单的拉普拉斯方程[3]：

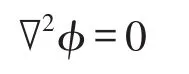
即产生静电场的电荷都分布于区域V的边界上，它们的作用通过边界条件反映出来。因此，这类静电场问题的解法是求拉普拉斯方程的满足边界条件的解。

3.1.2 基本步骤

A:判断求解区域内是否有电荷分布：如果没有电荷，可利用拉普拉斯方程求解；

B:拉普拉斯方程：∇2ϕ=0的通解为

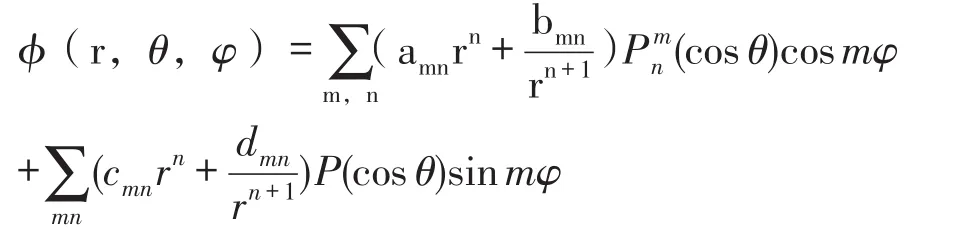
式中：amn；bmn；cmn；dmn为任意常数，由边界条件确定。

C:方程的解依赖于所求解区域的对称性，包括轴对称和球对称两种情况，

D:确定通解中的待定系数，依赖于求解区域的边界条件、边值关系，它对于求解静电场问题十分重要，大致有以下几种类型：

（2）给出导体上的电势，导体面上的边界条件为ϕ=ϕ0（给定常数）

（3）给出导体所带总电荷Q，在导体面上的边界条件为

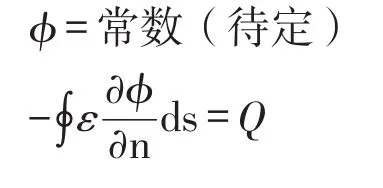
E:利用以上边界条件、边值关系，可以求解出通解中的待定系数，即可求得在特殊区域下的静电场电势的特解；

3.2 分离变量法的优点

分离变量法的优点是求解静电场时适用于考虑求解区域内没有自由电荷分布的区域，只有在界面形状比较简单的几何曲面时，这类问题的解才能以解析解形式给出，而且视不同区域的对称性和边界条件情况而定[4]；分离变量法求解静电场解题步骤思路比较清晰，学生在学习的过程中容易掌握；在利用边值关系和边界条件求解待定系数时，边界条件不多，学生很容易结合以上条件求解出特解。

4 镜像法

4.1 基本原理

在一些特殊情形下，如区域内只有一个或几个点电荷，区域边界是导体或介质界面，这类问题通常采用镜像法求解。在求解过程中提前设想存在某一个假想的点电荷来代替导体或介质表面的感应电荷或极化电荷，注意在这种替换下不能改变空间中的电荷分布，关键是在于能否满足边界条件。

4.2 基本步骤

（1）:判断是否符合镜像法求解的条件；

（2）:是否存在假想的电荷，初步估计它所在的位置；

（3）:通过满足的边界条件和边值关系以此来确定假想电荷的所带的电荷量和具体位置；

（4）:利用点电荷的电势公式，求解几个点电荷（已知点电荷和假想的点电荷）在空间区域内的电势；

4.3 镜像法求解的优点

镜像法的优点是适用于考虑求解区域内没有自由电荷分布的区域[5]，只在区域内有几个点电荷和导体或介质，假想点电荷的电荷量与位置依赖于边界条件情况而定；镜像法求解静电场关键是找出边界条件，学生依赖于分离变量法中涉及到的边界条件，在求解过程中很容易找出；利用假想的点电荷代替导体面的感应电荷和介质表面上的极化电荷，使复杂问题简单化，直接转换为点电荷电势的求解，学生对于点电荷电势的求解掌握的比较好，所以利用镜像法很容易求解出电势。

5 格林函数法

5.1 基本原理

求解一个点电荷的边值问题在静电学中有着重要的意义，因为这不仅意味着有关该点电荷的特殊问题得到了解决，而且还意味着有更广的一类边值问题可以借此而得到解决。如果边界条件是给定S上的电势ϕs，这类边值问题称为第一类边值问题；如果给定S上的，这类边值问题称为第二类边值问题。这些边值问题，都是怎样借助于有关点电荷的较简单的边值问题而得到解决的[6]，因此，须先引入点电荷密度δ函数的数学表达式，然后利用格林公式把一般边值问题和有关点电荷的相应问题联系起来，通过格林公式把静电场的边值问题转化为求解相应的格林函数问题，即此方法为格林函数法。

5.2 基本步骤

（1）:是否能满足δ函数；

δ函数定义如下：

δ(x)=0,当x≠0

∫vδ(x)dv=1，若积分区域V包含x=0点；

（3）:判定是否给定边界条件：ϕs或；

其中ϕ替换为G函数

E:在δ(x-x′)=0,当x≠x′，满足拉普拉斯方程；

在∫vδ(x-x′)dx=1,当x′∈V满足泊松方程；

则可利用分离变量法和镜像法求解结果将ϕ替换为G函数即可。

5.3 格林函数法的特点

利用格林函数法求解过程中，关键是看ρ(x)是否能满足δ函数的定义，将其改为ρ(x)=δ(x-x′)；如果满足边界条件，即可将ϕ替换为G函数，利用格林函数法求解。

6 结语

在近现代物理学中关于静电场问题的研究占有十分重要的地位，通过本文的论述分析，可以使学生掌握求解静电场问题的三种方法，充分了解三种方法求解静电场的基本原理、解题的基本步骤和特点。通过学习静电场这部分知识，既加深了对静电场的概念、定理及基本规律的理解，又获得了分析和处理一些静电问题的初步能力，为以后解决实际静电问题打下基础，更为以后进行求解静电场问题的教学研究夯实了基础，具有一定的指导意义。

［1］［2］郭硕鸿.电动力学（第三版）［M］.高等教育出版社,2008.

［3］尹真.电动力学（第二版）［M］.科学出版社,2006.

［4］陈世民.电动力学简明教程［M］.高等教育出版社,2004.

［5］虞福春，郑春开.电动力学［M］.北京大学出版社,1992.

［6］郑春开.电动力学解题指导［M］.北京大学出版社,2004.

O481.2

A

1671-6469（2016）-06-0106-04

2015-10-09

昌吉学院教研课题（14jyyb006）；新疆维吾尔自治区《探秘电和磁》视频公开课（新教高【2013】16号）。

郭福强（1980-），男，河南周口人，昌吉学院物理系副教授，研究方向：教学改革研究。