二维风险模型带交易费用的最优分红
2017-01-16岳毅蒙李江涛
岳毅蒙,王 欣,李江涛
(1.商洛学院数学与计算机应用学院,陕西商洛 726000;2.商洛学院经济与管理学院,陕西商洛 726000; 3.西安武警工程大学理学院,陕西西安 710086)
二维风险模型带交易费用的最优分红
岳毅蒙1,王 欣2,李江涛3
(1.商洛学院数学与计算机应用学院,陕西商洛 726000;2.商洛学院经济与管理学院,陕西商洛 726000; 3.西安武警工程大学理学院,陕西西安 710086)
研究带交易费用的二维风险模型的最优分红问题。以最大化分红与注资的折现之差为目标,利用随机控制理论,通过求解哈密尔顿-雅克比-贝尔曼(HJB)方程,得到了相应的最优分红策略。
注资;分红;HJB方程
二维风险模型是由Chan等[1]在2003年首次提出并给出了关于破产概率的一些重要结论。文献[2]中研究了二维风险模型的生存概率,文献[3]中研究了动态比例再保险和近似二维复合泊松风险模型的破产概率,文献[4]中研究了二维风险模型的最优分红和脉冲控制,文献[5]中研究了带注资的二维复合泊松模型的最优分红。结合文献[6-9],在前人研究的基础上,讨论带最小盈余约束和交易费用情况下,二维风险模型的最优分红与注资策略。
1 模型建立
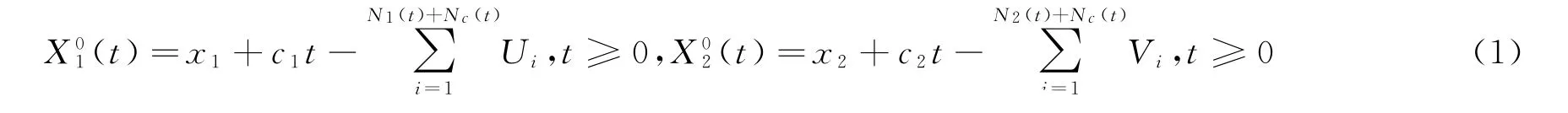
其中:x1x2为初始准备金;c1,c2(>0)为保费收入率;{N1(t)}t≥0、{N2(t)}t≥0、{Nc(t)}t≥0分别表示独立的强度为λ1、λ2、λc的Poisson过程;适应最小的右连续域流{F}t≥0;{Ui}、{Vi}分别表示一列正的、相互独立同分布的变量序列。在原模型基础上引入策略π={(Dt,Zt)},其中Dt{}和Zt{}分别表示0~t时刻的累积分红和累积注资。一个策略称为可行策略需满足:Dt{}是右连左极的,增的适应的过程,且满足D0-=0;{Zt}是左连右极的,增的适应的过程,且满足Z0=0。记所有可允许策略集为
则受控的盈余过程转化为
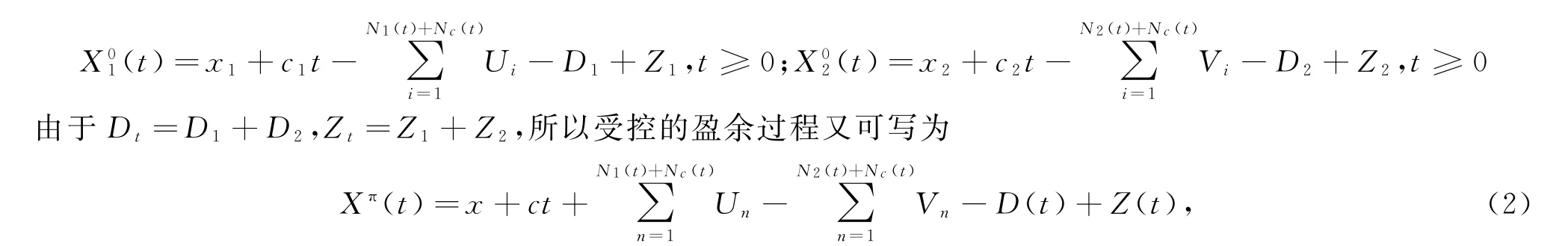
其中:x=x1+x2,c=c1+c2。
假设保险公司有最低盈余要求m>0,如果赤字太大,注资不合理,破产时刻定义为
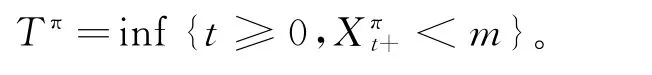
2 HJB方程和最优策略
引理1值函数V(x)在[m,∞)单调递增且对0≤y≤x有V(x)-V(y)≥β(x-y),且
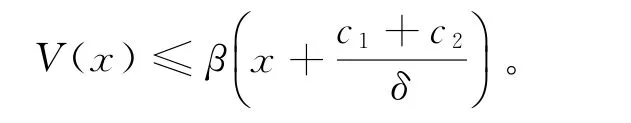
引理2若V(x)在[m,∞)为凹的,则最优注资上限a=m。
类似于文献[6]中的讨论,对x≥m及任意停时τ,有如下动态规划原理成立:
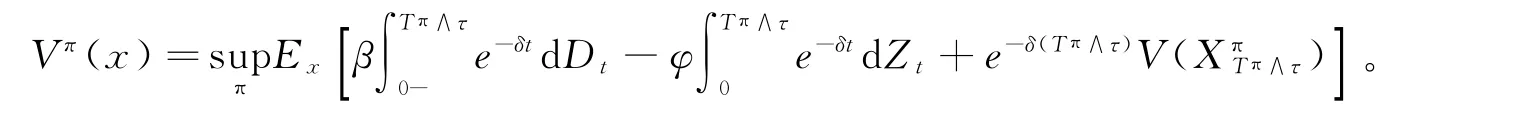
类似于文献[5]可得V(x)在[m,∞)上满足的HJB方程:
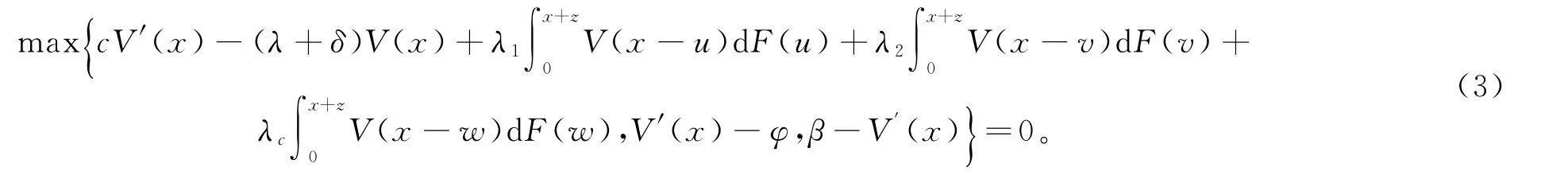
可以定义最优分红限b:=inf{x:V′(x)≤β}和最优注资上限a:=sup{x:V′(x)≥φ}∨m。现在定义策略如下:
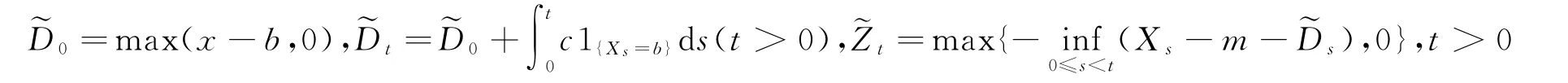
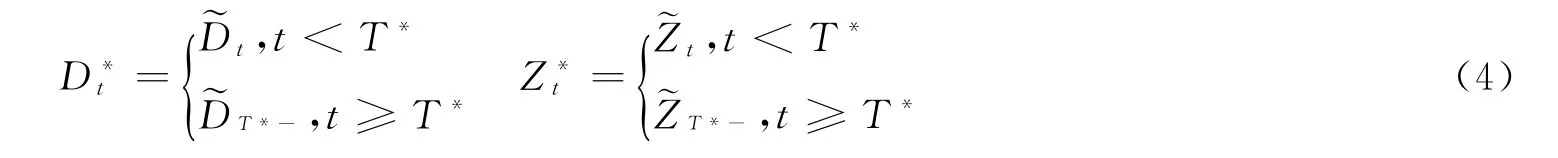
定理1若V(x)在[m,∞)是凹的,则策略(4)是最优策略,即Vπ∗(x)=V(x)。
证明设X∗(t)是策略(4)下的受控过程,当X∗(t)=b有V′(X∗(t))=1;当X∗(t)<b有V′(X∗(t))>1。运用It^o公式,有
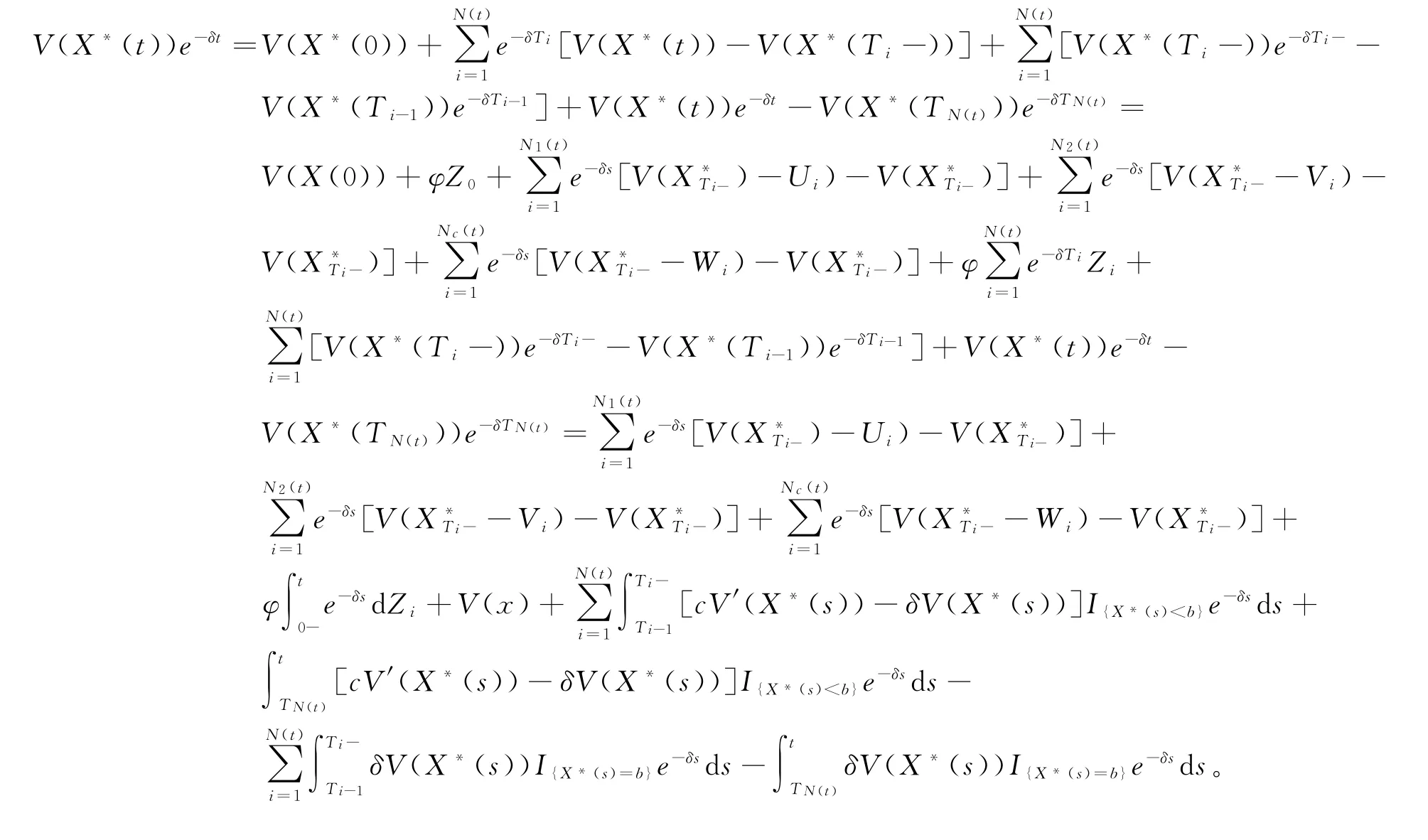
理赔到达时,有
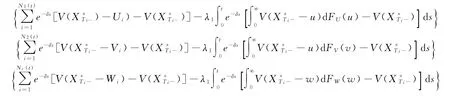
为均值为0的鞅。等价地,过程
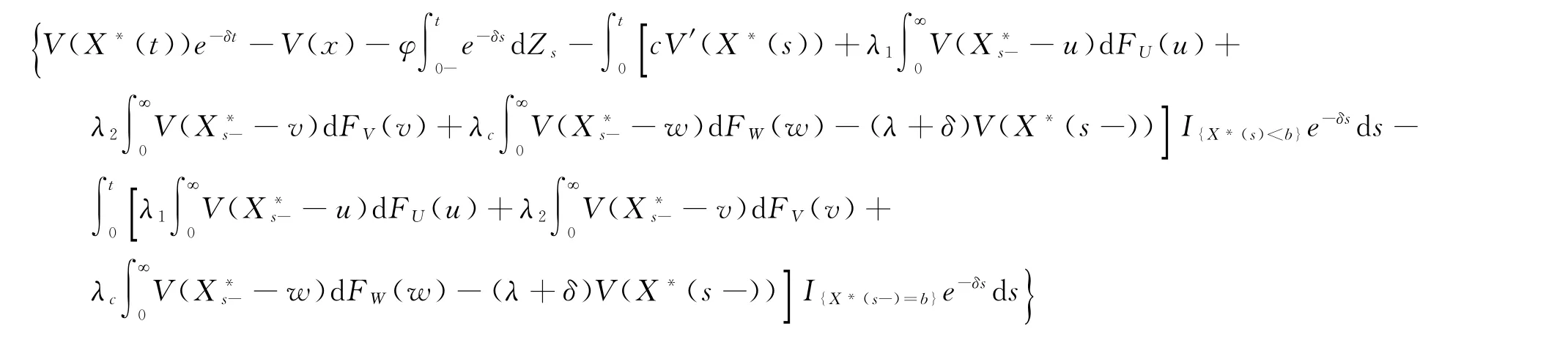
为鞅。又V(x)为凹的且左右可导。进一步我们假设FU,V(u,v)连续,因此V(x)满足式(3),且连续可微。
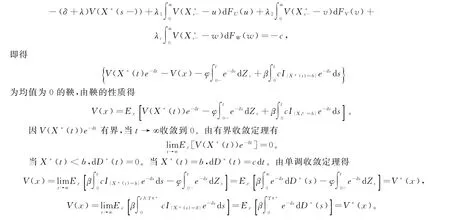
3 解的特征
定理2V(x)是HJB方程(3)的最小非负解。
证明设f(x)是HJB方程的非负解,那么f(x)递增。令X∗为最优策略下的受控过程,由定理1得
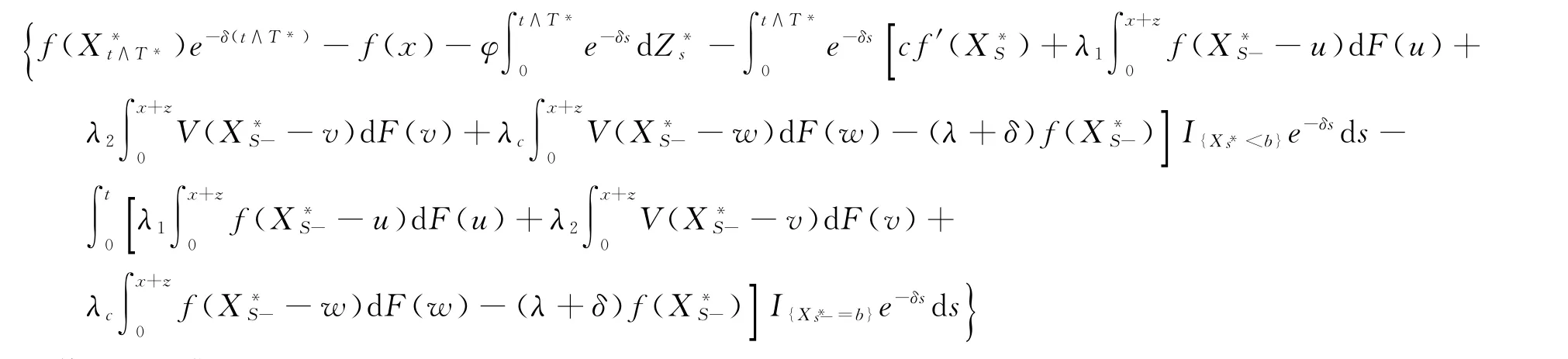
为均值为0的鞅。由HJB方程得
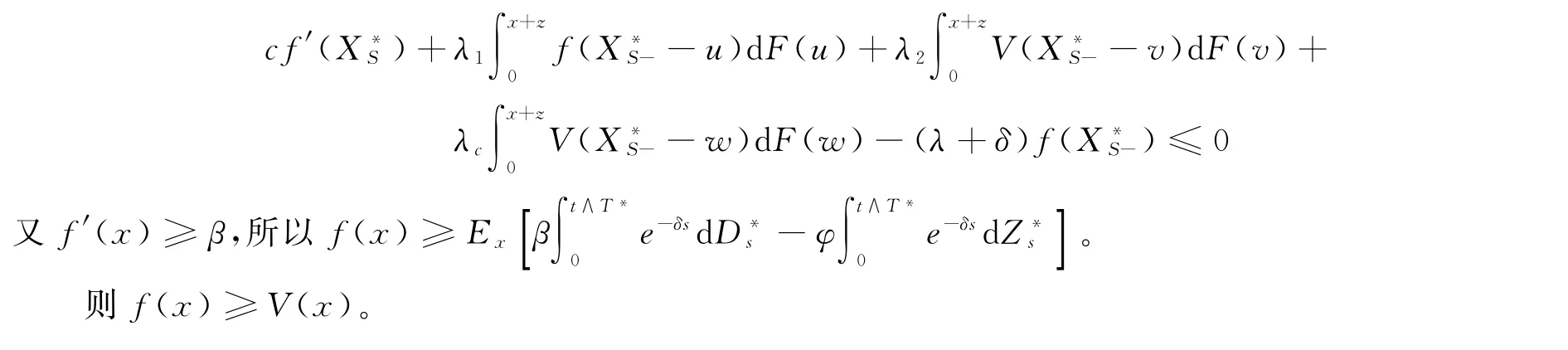
[1] Chan W C,Yang H L,Zhang L Z.Some Results on Ruin Probabilities in a Two-dimensional Risk Model[J].Insurance:Mathematics and E-conomics,2003,32(3):345-358.
[2] Dang L F,Zhu N,Zhang H M.Survival Probability for a Two-dimensional Risk Model[J].Insurance:Mathematics and Economics,2009,44 (3):491-496.
[3] Corporation H P.Dynamic Proportional Reinsurance and Approximations for Ruin Probabilities in the Two-dimensional Compound Poisson Risk Model[J].Discrete Dynamics in Nature&Society,2012,12(12):1 951-1 965.
[4] Czarna I,Palmowski Z.De Finetti's Dividend Problem and Impulse Control for a Two-dimensional Insurance Risk Process[J].Stochastic Models,2011,27(2):220-250.
[5] Zhang S Q.Optimal Dividend Payments of the Two-dimensional Compound Poisson Risk Model with Capital Injection[J].Operations Research Transactions,2012,16(3):119-131.
[6] Azcue P,Muler N.Optimal Reinsurance and Dividend Distribution Policies in the Cramer-Lundberg Model[J].Math.Finance,2005,15(2): 261-308.
[7] Bayraktar E,Kyprianou A E,Yamazaki K.Optimal Dividends in the Dual Model under Transaction Costs[J].Insurance:Mathematics and Economics,2014,54:133-143.
[8] Eisenberg J,Schmidli H.Minimising Expected Discounted Capital Injections by Reinsurance in a Classical Risk Model[J].Scandinavian Actuarial Journal,2011,3:155-176.
[9] 岳毅蒙.最小盈余约束下风险模型的最优分红策略[J].甘肃科学学报,2015,27(2):19-24.
Optimized Participation in Profit of Transaction Expenses in Two-dimension Risk Model Region
Yue Yimeng1,Wang Xin2,Li Jiangtao3
(1.School of Mathematics and Computer Application,Shangluo University,Shangluo726000,China; 2.School of Economics and Management,Shangluo University,Shangluo726000,China; 3.College of Sciences,Engineering University of CAPF,Xi’an710086,China)
Study the problem of the optimized participation in profit of transaction expenses in two-dimension risk model region.Aiming for the difference between the optimized participation in profit and discounting of capital injection,the corresponding strategy of the optimized participation in profit can be got by stochastic control theory and solve HJB equation.
Capital injection;Participation in profit;Hamilton Jocabi Bellman equation
O211.6
:A
:1004-0366(2016)05-0026-04
2015-08-07;
:2015-10-08.
陕西省教育科学“十二五”规划课题(SGH13406);商洛学院科研项目(15SKY011).
岳毅蒙(1984-),男,陕西富平人,硕士,讲师,研究方向为金融数学.E-mail:18740586401@126.com.
Yue Yimeng,Wang Xin,Li Jiangtao.Optimized Participation in Profit of Transaction Expenses in Two-dimension Risk Model Region[J].Journal of Gansu Sciences,2016,28(5):26-29.[岳毅蒙,王欣,李江涛.二维风险模型带交易费用的最优分红[J].甘肃科学学报,2016,28(5):26-29.]
10.16468/j.cnkii.ssn1004-0366.2016.05.007.
