伪Smarandache无平方因子函数与Euler函数的两个方程
2017-01-16王曦浛李国蓉
王曦浛,高 丽,李国蓉,薛 阳
(延安大学数学与计算机科学学院,陕西延安 716000)
伪Smarandache无平方因子函数与Euler函数的两个方程
王曦浛,高 丽,李国蓉,薛 阳
(延安大学数学与计算机科学学院,陕西延安 716000)
对任意的正整数n,著名的伪Smarandache无平方因子函数Zw(n)定义为最小的正整数m使得n|mn,利用初等方法以及伪Smarandache无平方因子函数Zw(n)和Euler函数φ(n)的性质,研究了方程Zw(φ(n))=φ(Zw(n))的可解性,证明了该方程有无穷多个正整数解。同时讨论了方程Zw(n)+φ(n)=2n的可解性,并求出了该方程的正整数解为n=1。
伪Smarandache无平方因子函数;Euler函数;正整数解
对任意的正整数n,著名的伪Smarandache无平方因子函数Zw(n)[1]定义为最小的正整数m使得n|mn,即Zw(n)=min{m∶n|mn,m∈N}。这个Zw(n)函数是由美籍罗马尼亚著名的数论专家Smarandache教授在他所著的《Only Problems, Not Solutions!》一书中提出来的,并建议人们研究其性质。而Euler函数φ(n)定义为不大于n且与n互素的正整数的个数。对于这两个函数许多学者对其进行了研究,并得出了有意义的结论[2-7],如文献[2]中研究了方程Zw(Z(n))-Z(Zw(n))=0的可解性,并证明了该方程有无穷多个正整数解,文献[3]中研究了方程Zw(n)=φ(n)与Zw(n)+S(n)=2n的可解性问题,文献[4]中讨论了Sk(n)=φ(n)的可解性,并给出该方程的所有正整数解,文献[5]中讨论了两个数论函数方程φ(n)=Z(nk)与Z(n)+φ(n)=2n的可解性问题,并给出所有的正整数解,文献[6]中讨论了关于Smarandache函数和Euler函数的三个方程的可解性问题并求出所有正整数解。
我们利用初等方法研究了方程Zw(φ(n))=φ(Zw(n))与Zw(n)+φ(n)=2n的可解性问题,并给出方程所有的正整数解。
1 相关引理
引理1对于素数p与α≥1,有φ(pα)=pα-1(p-1)[8]。
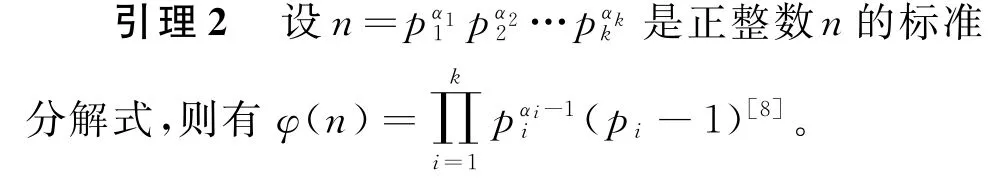
引理3设n是任意的正整数,有Zw(n)≤n,特别当n是无平方因子数时,则Zw(n)=n[9]。
引理4如果p为素数且k≥1,则Zw(pk)=p[]。
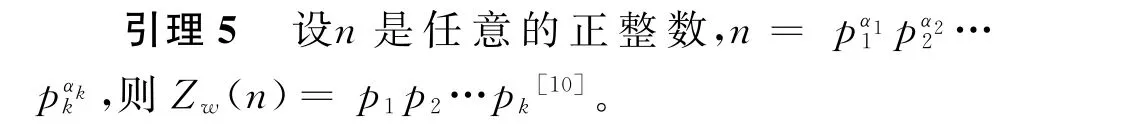
引理6若(m,n)=1,则Zw(m,n)=Zw(m)·Zw(n)[9]。
2 主要结论及其证明
定理1对任意的正整数n,方程
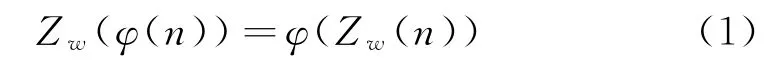
有无穷多个正整数解。
证明(1)显然当n=1时,Zw(φ(1))=1,φ(Zw(1))=1,故方程(1)成立。
(2)当n=p时,由引理1和引理4可知:Zw(φ(p))=Zw(p-1),φ(Zw(p))=φ(p)=p-1。若方程(1)成立,则Zw(p-1)=p-1。显然当p-1为无平方因子数时,Zw(p-1)=p-1成立,所以当n=p且p-1为无平方因子数即为方程(1)的解。
(3)当n=pα时,由引理1和引理4可知,Zw(φ(pα))=Zw(pα-1(p-1)),φ(Zw(pα))=φ(p)=p-1。此处对p分两种情况讨论:
(ⅰ)当p是奇素数时,α≥2,∵(pα-1,p-1)=1。由引理6可知:Zw(φ(pα))=Zw(pα-1(p-1))=Zw(pα-1)·Zw(p-1)=p·Zw(p-1)。若方程(1)成立,则p·Zw(p-1)=p-1,即Zw(p-1)=1-经检验方程(1)无解。
(ⅱ)当p=2时,有Zw(φ(2α))=Zw(2α-1),φ(Zw(2α))=φ(2)=1。若方程(1)成立,则Zw(2α-1)=1,即α=1。故当α=1,p=2,n=2,方程(1)成立。
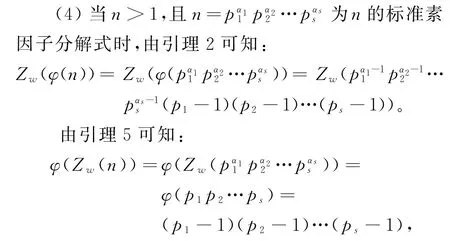
当α1,α2,…,αs全都为1时,显然有
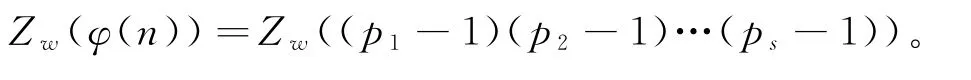
若式(1)成立,则
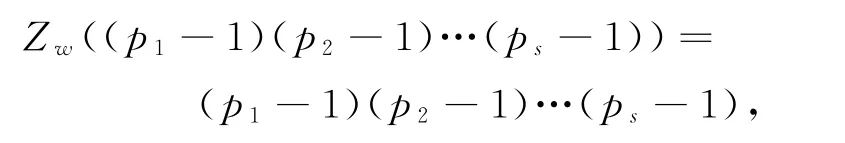
结论与引理3矛盾,因此方程(1)无解。
当α1,α2,…,αs不全为1时,又可以分两种情况讨论:
(ⅰ)当p1,p2,…,ps全为奇素数时,由引理2和
引理6可知:
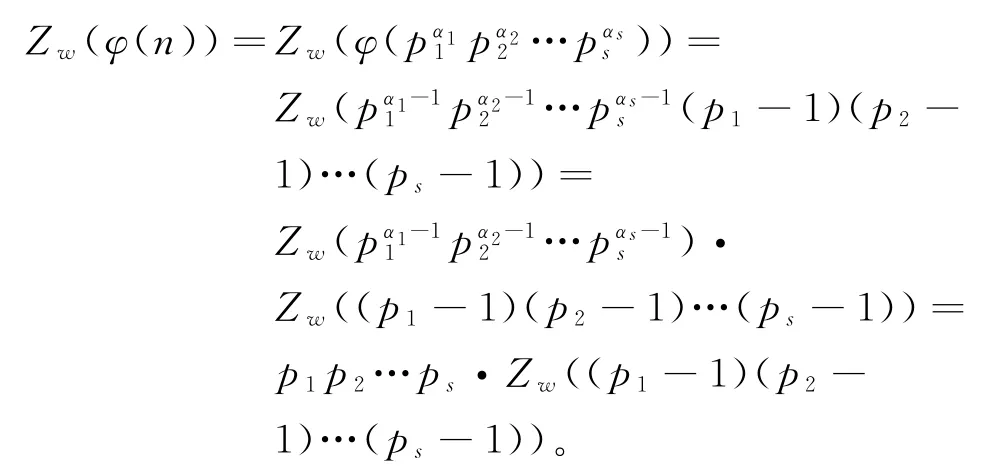
由引理5可知:
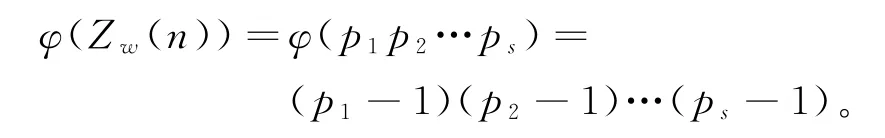
若方程(1)成立,则
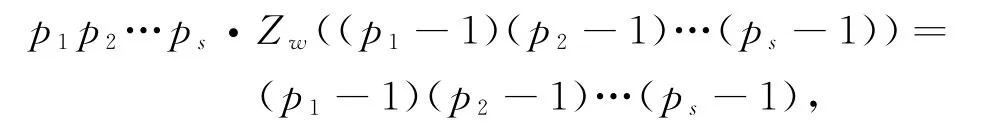
化简得
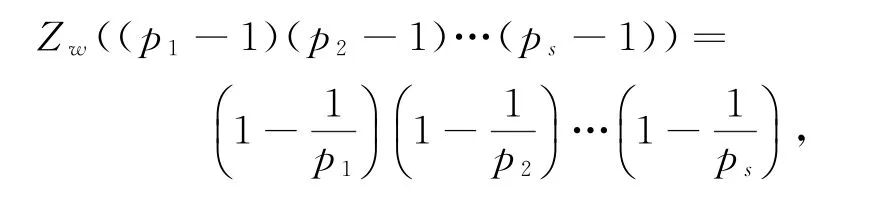
结论与引理3矛盾,则方程(1)无解。
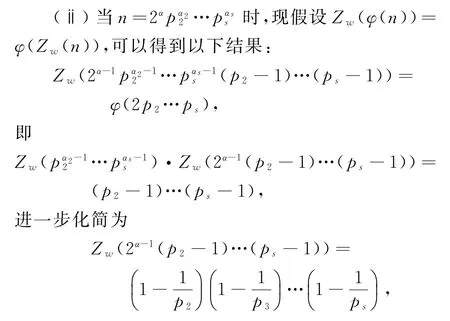
结论与引理3矛盾,则方程(1)无解。
综上所述,得到方程(1)有无穷多个正整数解。
定理2对任意的正整数n,方程
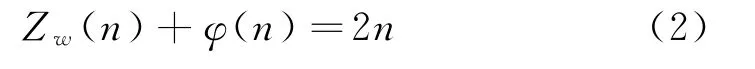
仅有正整数解n=1。
证明(1)当n=1时,由函数Zw(n)、φ(n)的定义,有Zw(1)=1、φ(1)=1,所以Zw(1)+φ(1)=2。
(2)当n=p时,由引理1和引理4可知
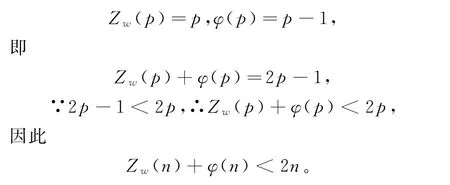
(3)当n=pα时,由引理1和引理4可知:Zw(pα)=p,φ(pα)=pα-1(p-1),则Zw(pα)+φ(pα)=p+pα-1(p-1)。此处对p分两种情况讨论:
(ⅰ)当p是奇素数时,α≥2有p+pα-1(p-1)<2pα,即Zw(n)+φ(n)<2n。
(ⅱ)当p=2时,有Zw(2α)=2,φ(2α)=2α-1,则Zw(2α)+φ(2α)=2+2α-1,∵2+2α-1<2·2α=2α+1,∴Zw(n)+φ(n)<2n。
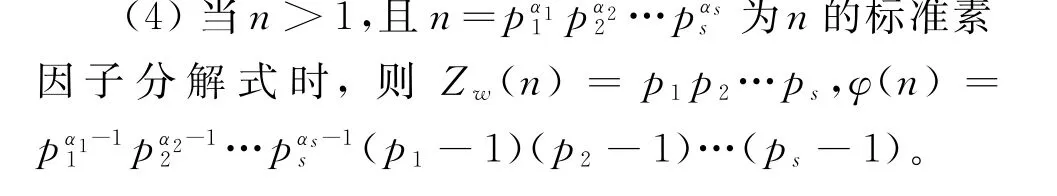
当α1,α2,…,αs全都为1时,显然有p1p2…ps+(p1-1)(p2-1)…(ps-1)<2p1p2…ps,即Zw(n)+φ(n)<2n。
当α1,α2,…,αs不全为1时,又可以分两种情况讨论:

综上所述,方程(2)仅有正整数解n=1。证毕。
[1] Smarandache F.Only Problems,Not Solutions[M].Chicago: Xiquan Publishing House,1993.
[2] 关文吉,郑亚妮.关于伪Smarandache函数的一个方程[J].纺织高效基础科学学报,2008,21(2):151-153.
[3] 王春萍.与Smarandache函数相关的一些方程[D].西安:西北大学,2010.
[4] 朱敏慧.一个包含Euler函数及k阶Smarandache Ceil函数的方程及其正整数解[J].纯粹数学与应用数学,2009,25(2): 414-416.
[5] 高丽,鲁伟阳,郝虹斐.包含伪Smarandache函数与Euler函数的两个方程[J].陕西科技大学学报,2013,31(6):163-165.
[6] 范盼红.关于F.Smarandache函数和欧拉函数的三个方程[J].黑龙江大学自然科学学报,2012,29(5):626-628.
[7] 祁兰,赵院娥.关于Smarandache Ceil函数的一个混合均值[J].甘肃科学学报,2014,26(3):12-13.
[8]Tom M.Apostol.Introduction to Analytic Number Theory [M].New York:Spring-Verlag,2012.
[9]Felice Russo.A Set of New Smarandache Functions,Sequences and Conjectures in Number Theory[M].Lupton USA:American Research Press,2000.
[10] Le Maohua.On the Pseudo-Smarandache Squarefree Function [J].Smarandache Notions Journal,2002,13(1-2-3):229-236.
Two Equation of Fake Smarandache Square-free Factor Function and Euler Function
Wang Xihan,Gao Li,Li Guorong,Xue Yang
(College of Mathematics and Computer Science,Yan’an University,Yan’an716000,China)
For any positive integern,the famous fake Smarandache square-free factor functionZw(n)is defined as positive integerm,n|mn,with primary method and fake Smarandache square-free factor functionZw(n)and Euler functionφ(n),this text studies solvability of equationZw(φ(n))=φ(Zw(n)),and proves that this equation has infinitely many integer solutions.Meanwhile,it discusses the solvability ofZw(n)+φ(n)=2n,giving its positive integer solution thatn=1.
Fake Smarandache square-free factor function;Euler function;Positive integer solution
O156.4
:A
:1004-0366(2016)05-0023-03
Wang Xihan,Gao Li,Li Guorong,et al.Two Equation of Fake Smarandache Square-free Factor Function and Euler Function[J].Journal of Gansu Sciences,2016,28(5):23-25.[王曦浛,高丽,李国蓉,等.伪Smarandache无平方因子函数与Euler函数的两个方程[J].甘肃科学学报,2016,28(5):23-25.]
10.16468/j.cnkii.ssn1004-0366.2016.05.006.
2016-04-13;
:2016-05-26.
陕西省科技厅科学技术研究发展计划项目(2013JQ1019);延安大学校级科研计划项目-引导项目(YD2014-05);延安大学研究生教育创新计划项目.
王曦浛(1990-),女,陕西乾县人,硕士研究生,研究方向为数论.E-mail:648034259@qq.com.
高丽.E-mail:yadxgl@163.com.
