光大生物质发电厂取水工程对通航影响的数学模型研究
2017-01-16许莎莎
许莎莎
(安徽省交通勘察设计院有限公司,安徽 合肥 230011)
光大生物质发电厂取水工程对通航影响的数学模型研究
许莎莎
(安徽省交通勘察设计院有限公司,安徽 合肥 230011)
基于有限单元方法,建立了平面二维水流数学模型,对取水口边界条件进行了研究。利用该模型计算了光大生物质发电厂取水工程建设前、后取水建筑物及其附近航道的流速、流向和水位等水流特性,分析了典型控制水位下,取水口建筑物及其取水对航道通航条件的影响,结果表明:取水工程不会对通航产生影响。
有限体积;数学模型;取水口;通航条件
对于取水工程对水动力条件影响的数学模型研究,已经在实际中得到了一些应用,数值模拟在工程建设影响论证方面已经成为一种趋势,但是目前取水工程的建设对通航的影响的数学模型研究仍然较少,对取水口边界条件的研究也有待深入。本研究建立了一个二维水流数值模型对取水口附近水域水流流态进行计算,利用该模型对光大生物质电厂取水口工程对通航的影响进行了研究,定量分析了取水口附近航道工程前、后水流流速和流向变化情况。
1 数学模型基本理论和方法
数学模型有一维、二维和三维之分,一维模型无法模拟出局部的水流条件,在使用上很受限制;三维模型的计算较为复杂耗时,且在实际应用中,对于复杂的边界处理及资料验证仍有较大的困难。对于只需要了解取水口取水对通航的影响,不需要充分了解取水口附近水体的三维流动特性时,用平面二维模型来模拟河道的流动特性应是最好的选择。
1.1 控制方程
大部分河流湖泊都是浅水水流,满足以下假定:① 具有自由表面;② 以重力为主要的驱动力,以水流和固体边界之间及水流内部摩阻力为主要的耗散力;③ 水平流速沿水深近似成均匀分布;④ 垂向流速和垂向加速度可忽略,水压接近静压分布。基于以上假定,对三维水流的运动方程沿水深进行积分,可得二维浅水水流控制方程:
(1)连续性方程。
(1)
(2)动量方程。
(2)
(3)
1.2 定解条件
(1)初始条件:给定初始时刻t=0时,计算域内所有计算变量(u,v,ξ)的初始值。
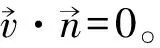
1.3 离散方法
本次采用非结构有限体积法离散控制方程。有限体积法中使用的非结构网格通常由三角形或四边形网格构成,为了准确的逼近水下地形,这里仅采用三角形网格。
2 模型验证
2.1 取水工程概况
(1)取水河段情况。光大怀远生物质发电厂工程位于于安徽省怀远县城西侧,电厂取水口位于涡河南岸,位于蒙城闸下,具体位置为北纬32.96°,东经117.01°。距离上游控制节点为蒙城闸约71km,下游水位受下游蚌埠闸水利枢纽控制,距离蚌埠闸约18km,取水口距离何巷闸约8km。
(2)取水设计方案。水泵房设置在光大怀远生物质发电厂内东北角。利用设在河床中的取水头部和自流引水管取水至泵房。取水建(构)筑物包括取水头、自流引水管和补给水泵房。
取水头拟采用钢混箱式,取水头上设格栅。箱式取水头部伸入河道深处,尺寸为4.5m×1.5m×1.45m。为满足95%枯水位的取水要求,箱式取水头部内顶标高约15.0m,底标高13.55m,自流引水管中心线标高约14.30m,采用钢管桩架固定。设计取水流量0.3m3/s,取水方式为双管单侧取水。
2.2 研究内容
选用平面二维水流数学模型对目标河段进行模拟计算,并具体分析:① 工程实施前后水面线变化;② 工程实施前后航道附近流速变化。分析采用最不利工况进行模拟,即枯水期取水断面处设计最低通航水位15.67m,对应流量为0。
2.3 模型范围及网络概化
根据河道特性及取水口位置,本次计算将二维模型的研究范围确定为取水口上游3km至下游2km之间河段。为较好地反映河道地形及岸线的变化,模型采用非结构三角网格,网格空间步长约30m。为较好的反映工程实施后取水口附近的流场变化,取水口附近网格加密至1m左右。取水口概化为点源。为较好的反映河道当前的地形条件,选取2015年实测地形为模型计算地形。本次计算根据河道实际情况,并参考文[5],将河段主槽糙率选定为0.026,滩地为0.04。
2.4 模型计算及分析
(1)水面线变化。对工程实施前后各工况条件下水面线进行模拟计算,提取分析取水断面上下游50m范围内河道纵向水面线的变化。如图1所示,为工程实施前后,取水断面上下游50m范围内水面线对比图。从图中可看出,工程实施以后枯水期工况水位几乎无变化。
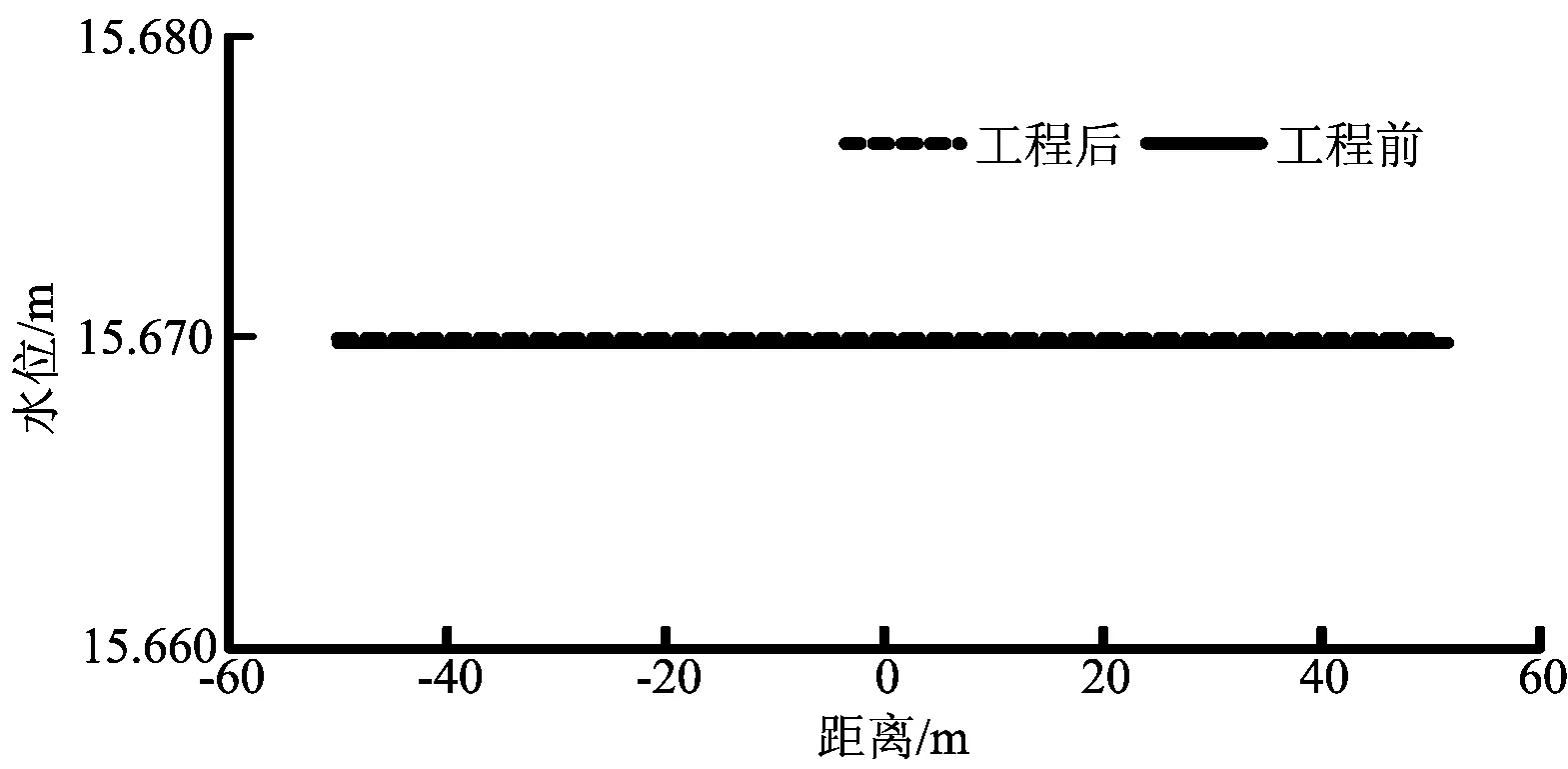
图1 枯水期工况取水断面上下游50m范围内纵向水面线变化
(2)流场计算。对工程实施前后取水断面附近河段流场进行模拟计算,分析水流流场特点。
工程实施后,取水口附近出现明显的横向水流,但流速较小。取水口附近3m范围内,流速值在0.13m/s~0.05m/s之间;距取水口3m~10m范围内,流速值在0.05m/s~0.01m/s之间;距取水口10m以外水域,流速值小于0.01m/s。在该工况条件下,最大纵向流速0.01m/s,最大横向流速0.06m/s。
3 结 论
本研究得到结论如下:① 从取水对通航影响的角度来看,当水位越低,流量越小,取水所造成的影响就越大。② 取水口周围50m范围内,取水口抽水对水位不产生影响,因此对河道通航水深不产生影响。③ 取水过程中,会改变取水口附近的流场,形成横流和回流结构,对整个河段的流场流态影响较小,横向流速在绝大部分范围内不超过0.03m/s,只有在取水口局部很小(小于10m内)的范围影响稍大些,但也不超过0.06m/s。④ 该取水工程取水时不会对航道正常的通航产生影响,本研究建立的平面二维数学模型能够较好地用于取水工程对航道通航条件影响的研究。
[1] 钟伟华.论取水口通航论证的重要性[J].珠江水运,2007,(12):45-46.
[2] 汪建乐,刘明俊,张景程,等.取水口对船舶通航环境的影响 [J].交通信息与安全,2009,(27):57-59.
[3] 贲鹏,虞邦义,倪晋.淮河干流正阳关至吴家渡段水动力数学模型及应用[J].水利水电科技进展, 2013,(5):42-46.
[4] 虞邦义,杨兴菊,倪晋 淮河干流行洪区泄流能力研究[J].水动力学研究与进展,2014, (1):125-130.
[5] 刘玉年,何华松,虞邦义. 淮河中游河道特性与整治研究[M].北京:中国水利水电出版社,2012.
(责任编辑 陈化钢)
Mathematical model of the influence of intake project on navigation in Everbright biomass power plant
XU Sha-sha
(Anhui Provincial Communications Survey and Design institute Hefei 230011;China)
Based on the finite element method, a two-dimensional flow mathematical model for water intake boundary conditions are studied. Using the model to calculate the flow characteristics including flow velocity and water level ,before and after Everbright biomass power plant intake project building and its nearby. Focuses on the analysis of typical control water level and water intake structures on channel navigation condition the influence scope and degree. The results show that the water diversion project will not affect the navigation.
finite volume;mathematical model;intake;navigation condition
2016-05-28;
2016-09-01
许莎莎(1987-),女,安徽合肥人,助理工程师 ,从事水运工程项目管理。
10.3969/j.issn.1671-6221.2016.04.003
TM743
A
1671-6221(2016)04-0007-03
