盲人探路负梯度方向法
2017-01-16李春明
李春明
(中国石油大学(华东)胜利学院,山东东营 257061)
盲人探路负梯度方向法
李春明
(中国石油大学(华东)胜利学院,山东东营 257061)
负梯度方向法作为一个常用的优化方法在机械工程领域发挥着重要作用,但是,因其锯齿现象而具有计算量大、计算效率低的缺点。一维盲人探路寻优思想总结为:根据探测点与极值点相对位置的三种情况采取三种处理方案。基于此,将负梯度方向法进行了改进,提出了新的寻优方法——折线负梯度方向法。算法分为四部分:初始步长检验阶段;步长加倍探测阶段;暂不减半步长阶段;步长减半探测阶段。第三部分考虑了探测点远未及极值点的情况。提供了寻优思想流程图和完整的C语言子程序。通过与负梯度方向法的比较,证明了折线负梯度方向法具有计算量小、寻优效率大的特点。考虑远跨过极值点的情况,提出了走一步退半步探的算法。通过对不进行退半步探运算和退半步探时不减半步长两种情况的比较,证明了折线负梯度方向法的适用范围较广。
优化方法;负梯度方向法;盲人探路寻优思想;计算量
目前,优化方法在机械、冶金、石油、化工、电机、建筑、铁路、交通、航空、航天、航宇、国防、造船、纺织、轻工、机床、汽车、自动控制系统、电力系统、电子、电器、管理等工程设计领域均发挥着重要的作用,在数值仿真等领域也体现出优化理念,如三维数字化工艺模型、数字成像技术[1]、系统可靠性分析[2]等。即使是最简单的一维优化方法(单目标优化),也在机械行业得到了广泛的应用,如淬火工艺参数的确定和以可靠性为中心的预防性维修计划[3]。基于其他理论的优化方法也有较深入的研究,如遗传算法、广义鞍点问题[4]。
自外点惩罚函数法(土堆法)的有效性获得认可以来,优化方法已经发展成一个理论性强、系统性强的学科,其理论体系主要包括一维优化方法、多维无约束优化方法、多维有约束优化方法、线性优化方法、多目标优化方法、离散变量优化方法、基于生理学理论的优化方法、基于物理学理论的优化方法等。其中一维盲人探路优化方法[5]对一维优化方法的补充和多维优化方法的改进起到了重要作用[6]。
负梯度方向法利用当前点的局部信息获得目标函数下降量最大的方向作为寻优方向,当寻优点接近于极值点时,由于相邻寻优方向相互垂直,在每个寻优方向上所求得极值点与初始点的距离逐渐减小,并且每个寻优方向仍须采用一维优化方法获得最优点,须至少探测初始步长与收敛精度值之商的若干倍,也就是说,寻优效率逐渐变小,这称为锯齿现象。目前国内外的研究不仅应用范围较广[7-9],而且多主要集中在共轭梯度上[10,11]。负梯度方向法的深入研究也较多。研究将一维盲人探路优化方法的寻优思想推广应用于多维优化问题,根据负梯度方向法的寻优方向确定方法,提出了折线负梯度方向法。
1 一维盲人探路优化算法
在单峰假设(目标函数在寻优方向上有且只有一个极值点)下,从当前点开始,每一步所得探测点如果优于当前点,则将其置为当前点。从初始当前点出发,以初始步长向前探测,如果探点不如当前点好,则转身探测,如果探点仍不好,则说明极值点在单步范围之内,否则,每探一步加倍步长,直到探测点不如当前点好为止。此时,极值点在单位步长范围之内。减半步长探测,如探测点不好,可转身探测,如果探测点还不好,则减半步长探测与转身探测交替进行,直到探测点优于当前点为止,然后减半步长探测。重复以上过程,直到步长足够小时结束寻优。图1为该算法的流程图。图2为该算法寻优思想的流程图。

图1 一维盲人探路法的程序流程Fig.1 One-dimensional pathfinding program flow chart

图2 盲人探路法寻优思想流程Fig.2 Optimizing thoughts flow chart for blind person exploring way
2 基于盲人探路的折线负梯度方向法
2.1 寻优思想
每一步探测均沿当前点的负梯度方向进行。在每一个寻优方向上,均探测一个比当前点好的点,利用效率较大,符合渐进寻优特点。在一维盲人探路法的基础上增加以下三点:
(1)考虑到在新的寻优方向上探测点远未及极值点的情况,当极值点可能在单步步长之内时,暂采用上一个寻优方向上的寻优步长,如果探测点好则设置为当前点。因为新寻优方向上的极值点与前一寻优方向上的极值点不会在以当前点为圆心的同一个圆上,如果直接减半步长则容易失去捕捉极值点的机会。
(2)在暂不减半步长阶段,更新当前点之前,退半步探测,以避免探测点远跨过极值点而降低寻优效率。
(3)更新当前点之后,确定目标函数在该点处的负梯度方向,并将其单位化。寻优方向单位化在优化方法当中非常重要,可以保证在设计空间中探测点与当前点之间的距离为当前点步长。寻优方向通常用方向向量表示,表现为列阵的形式。如果不进行方向单位化,则会出现初始步长过大或过小的情况,从而导致算法失效。
寻优算法可分四个阶段:初始步长检验阶段;步长加倍探测阶段;暂不减半步长阶段;步长减半探测阶段。由于寻优方向为当前点的负梯度方向,只须步长的减半和加倍,而不须寻优方向的反向,所以,折线盲人探路法比一维盲人探路法的算法更加简洁。
2.2 算法流程图
根据盲人探路寻优思想及上述改进算法,改进的负梯度方向法流程如图3所示。

图3 折线负梯度方向法的寻优思想流程图Fig.3 Optimizing thoughts flow chart of broken line negative gradient direction method
2.3 算法步骤
(1)选定初始点x(1)为当前点,初始步长h=h0,收敛精度值ε(<h/10),计算当前点的目标函数值y1=f(x(1)),令寻优方向为当前点的负梯度方向s(1)。
(2)取探测点为x(2)=x(1)+hs(1),计算探测点的目标函数值y2=f(x(2))。
(3)如y1<y2,则令h=0.5h,如果h足够小,则取当前点为最优点,结束寻优,否则转步骤(2)。
(4)令h=h+h,y1=y2,x(1)=x(2),令寻优方向为当前点的负梯度方向s(1),取探测点x(2)=x(1)+hs(1),计算其目标函数值y2=f(x(2))。
(5)如y1≥y2,则转步骤(4);否则,令h=0.5h。
(6)产生新的探测点x(2)=x(1)+h,计算其目标函数值y2=f(x(2))。如果满足收敛条件则结束寻优。
(7)如y1≥y2,则令y1=y2,x(1)=x(2),退半步探,根据探测点决定是否再次更新当前点,寻优方向为当前点的负梯度方向s(1),转步骤(6);否则,令h=0.5h。
(8)产生新的探测点x(2)=x(1)+h,计算其目标函数值y2=f(x(2))。如果h足够小,并且x(2)与x(1)两点的目标函数值之差满足收敛准则,则取当前点与探测点的较好点为最优点,结束寻优。
(9)如y1≥y2,则令y1=y2,x(1)=x(2),h=0.5h,令寻优方向为当前点的负梯度方向s(1),转步骤(6);否则,令h=0.5h,转步骤(8)。
上述算法步骤中,(1)、(2)、(3)为初始步长检验阶段,(4)、(5)为步长加倍探测阶段,(6)、(7)为暂不减半步长阶段,(8)、(9)为步长减半探测阶段。
2.4 计算子程序部分代码


3 算例分析
对于无约束优化问题

取收敛精度值ε为1.0×10-5,采用负梯度方向法寻优,以[-10 8]T为初始点,采用目标函数值落差收敛准则和目标函数梯度准则均获得最优点为[2.499 9 2.500 1]T,最优解为7.207 9×10-8,最优点梯度为[0.000 5 -0.000 6]T的寻优结果,目标函数调用517次[12]。
取同样的初始点和收敛精度值,采用目标函数值落差和寻优步长均小于收敛精度值的收敛准则,采用基于盲人探路寻优思想的折线负梯度方向法,不进行走一步退半步测的步骤,寻优结果为:最优点[2.500 0 2.500 0]T;最优解3.326 0×10-10;最优点处的梯度[-2.379 9×10-54.872 3×10-5]T;目标函数调用次数为68。与负梯度方向法相比,经过47次寻优方向确定和57次目标函数调用即超过其寻优精度,可见,其计算量大大地减小,计算精度大大地提高。
图4和图5为寻优过程,其中曲线及数字表示目标函数等值线及其目标函数值,折线表示寻优过程,宝石形的点表示依次更新的当前点。可见,合理地增倍和减半寻优步长,有效地逼近了极值点。由于横坐标与纵坐标的刻度不一致,寻优步长并不代表实际长度。
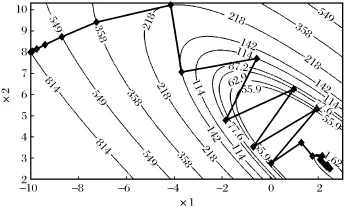
图4 不进行退半步探的寻优过程Fig.4 Optimizing process of non back half step

图5 接近于极值点的寻优过程Fig.5 Optimizing process on the verge of extreme point
从寻优过程可见,第三部分对于探测点在寻优方向上远未及极值点的情况可起到加大寻优效率的作用,但是对于探测点在寻优方向上越过极值点的情况考虑不足。如果在步长减半之前反向探半步,即走一步退半步探,则可以弥补上述不足。但是对于本例,其他条件不变,则增加了计算量;经过58次寻优方向确定、64次当前点更新和101次目标函数调用超过了负梯度方向法的寻优精度;最终经过69次寻优方向确定、76次当前点更新和119次目标函数调用获得寻优结果为:最优点[2.500 0 2.500 0]T、最优解6.759 9×10-10、最优点处的梯度[-3.209 5× 10-57.116 8×10-5]T。寻优过程如图6所示。可见寻优方向过早地减半会影响寻优效果。

图6 增加“走一步退半步探”的寻优过程Fig.6 Optimizing process of adding“up one step and back half step”
如果在退半步探之后步长不减半,则寻优过程如图7所示。

图7 退半步探时不减半步长的寻优过程Fig.7 Optimizing process without reduced half step length when backing half step
4 结论
通过对不进行退半步探运算和退半步探时不减半步长两种情况的比较,验证了以上所提出方法的有效性。对于具体问题,三种情况的计算量不同,在解决实际优化问题时,可根据要求适当地选用计算步骤,但是,寻优结果将是相同的。虽然基于盲人探路思想的折线负梯度方向法比负梯度方向法的计算量小,但是仍然是越接近于极值点寻优效果越差,这是由负梯度方向表示目标函数局部特性的事实所决定的。
[1] 赵娟娟.数字图像边缘检测方法的对比分析及优化[J].甘肃科学学报,2012,24(3):143-146.
[2] 李冬娜,张民悦,张霞.系统可靠性模糊方法优化问题[J].甘肃科学学报,2013,25(2):28-30.
[3] 王灵芝,徐宇工,张家栋.基于设备有效度和可靠度的预防修经济优化模型[J].机械工程学报,2010,46(4):163-168.
[4] 刘丽华,马昌凤,唐嘉.求解广义鞍点问题的一个新的类SOR算法[J].计算数学,2016,38(1):83-95.
[5] Li Chunming.Blind-walking Optimization Method[J].Journal of Networks,2010,5(12):1 458-1 466.
[6] 李春明.随机方向法改进及其验证[J].计算机仿真,2009,26 (1):189-192.
[7] Krejic,Nataša.A Gradient Method for Unconstrained Optimization in Noisy Environment[J].Applied Numerical Mathematics,2013,70(1):1-21.
[8] Narushima,Yasushi.Global Convergence of a Memory Gradient Method for Unconstrained Optimization[J].Computational Optimization and Applications,2006,35(3):325-346.
[9] Zheng Yue.A New Variant of the Memory Gradient Method for Unconstrained Optimization[J].Optimization Letters, 2012,6(8):1 643-1 655.
[10] Ezzati,Ghasem.A New Reliability Analysis Method Based on the Conjugate Gradient Direction[J].Structural and Multidisciplinary Optimization,2015,51(1):89-98.
[11] Narushima,Yasushi.Conjugate Gradient Methods Based on Secant Conditions that Generate Descent Search Directions for Unconstrained Optimization[J].Journal of Computational and Applied Mathematics,2012,236(17):4 303-4 317.
[12] 李春明.优化方法[M].南京:东南大学出版社,2009.
Negative Gradient Direction Method for Blind Person Exploring the Way
Li Chunming
(Shengli College,China University of Petroleum,Dongying257061,China)
Negative gradient direction method,a common used optimizing method,plays important effect in mechanical engineering field,but,it has the disadvantages of huge calculating amount and low calculating efficiency due to sawtooth phenomenon.One-dimensional blind person pathfingding and optimizing thoughts can be summed as:take three measurements according to 3 situations in relative position of probe point and extreme point.Based on this,improve the negative gradient direction method and give new optimizing method-broken line negative gradient direction method.The algorithm is classified into four parts: initial step length inspecting period;inspecting period for double step lengths;the period for temporarily not reducing step length;probing period for half step length.In third part,probe point far end and extreme point are considered.This text offers optimizing thought flow chart and complete C language subprogram.Compared with negative gradient direction method,broken line negative gradient direction method has the advantage of little calculating amount and high optimizing efficiency.Thinking about the situation of striding extreme point,this text gives the algorithm of up one step and back half step.By comparing algorithms of non back half step and non reduced length with back half step,it proves that broken line negative gradient direction method is widely used.
Optimizing method;Negative gradient direction method;Optimizing thoughts for blind person exploring way;Calculating amount
O224;TP202
:A
:1004-0366(2016)05-0116-07
2016-03-31;
:2016-05-04.
李春明(1971-),男,山东夏津人,博士后,副教授,研究方向为创新方法、优化方法、机械工程等.E-mail:lchming@126.com.
Li Chunming.Negative Gradient Direction Method for Blind Person Exploring the Way[J].Journal of Gansu Sciences,2016,28(5):116-122.[李春明.盲人探路负梯度方向法[J].甘肃科学学报,2016,28(5):116-122.]
10.16468/j.cnkii.ssn1004-0366.2016.05.026.
