M-QAM OFDM系统功放非线性分析*
2017-01-16樊小琴
樊小琴,王 菊,吉 磊
(中国电子科技集团公司第三十研究所,四川 成都 610041)
M-QAM OFDM系统功放非线性分析*
樊小琴,王 菊,吉 磊
(中国电子科技集团公司第三十研究所,四川 成都 610041)
M-QAM调制的OFDM系统峰均比较高,而放大器的非线性会导致系统性能的下降。分析放大器非线性对M-QAM调制的OFDM系统性能的影响,将非线性影响总结为两类:星座图旋转和非线性噪声。采用训练序列来估计星座图的旋转角度,并仿真非线性噪声的统计特性和不同静态工作点条件下的误码率曲线,最后给出一种输出功率与信噪比损失的权衡方法。工程应用中,当已知功放的特性曲线和调制参数时,可依照该方法快速计算链路的解调信噪比损失和总体性能损失,并确定功放的最佳静态工作点。
M-QAM OFDM;功率放大器;最佳静态工作点;星座图
0 引 言
由于频谱效率高,M-QAM调制的正交频分复 用(Orthogonal Frequency Division Multiplexing,OFDM)已在LTE(Long Term Evolution)[1]﹑数字视频广播(DVB)[2]﹑电力线通信[3]﹑高清数字电视(HDTV)[4]等领域得到广泛应用。但是,M-QAM调制的OFDM存在较高的峰均比[5],会由于功放的非线性,给M-QAM OFDM系统带来性能损失。
文献[4]将功放非线性建模为软限幅器,分析了限幅对多分辨率(MR)64-QAM OFDM误码率的影响,指出0.1%的限幅概率对MR 64-QAM OFDM造成的信噪比损失可以忽略。文献[6-7]将非线性干扰建模为加性白高斯噪声,推导了在非线性失真和相位噪声共同影响的循环前缀OFDM误码率。值得注意的是,文献[6-7]采用了高斯近似的方法,推导的理论曲线与仿真曲线存在差别,信噪比越高,差别越大。
本文将功放的非线性影响归结为两类:星座图旋转和非线性噪声。星座图旋转采用训练序列的方式估计后再补偿,仿真绘制出非线性噪声的概率密度函数,并与高斯近似的概率密度函数对比,分析了高斯近似和理论误码率差别的原因,同时给出了选择功放最佳静态工作点的方法,从而为工程应用提供理论依据。
1 M-QAM OFDM系统模型
1.1 M-QAM OFDM信号模型
受放大器非线性影响的M-QAM OFDM等效基带模型见图1。
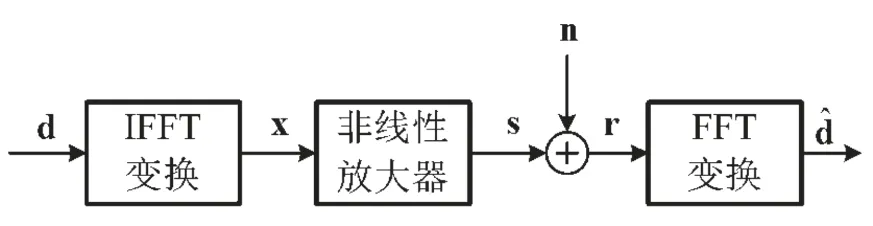
图1 M-QAM OFDM系统模型
第k帧接收信号等效基带矢量rk可以表示为:
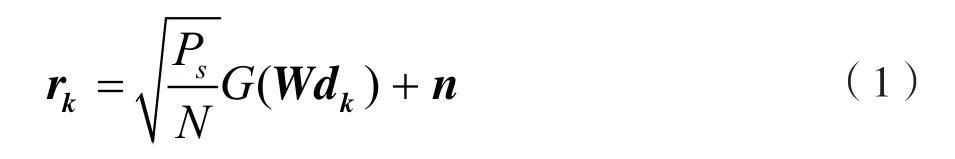
式中,Ps为发端功率,N为OFDM子载波的个数,表示第k帧中第i个M-QAM基带调制数据,n=[n0,n1,…,nN-1]是方差为N0T/2的加性白高斯噪声矢量,N0/2是双边功率谱密度,T是单个OFDM符号的有效持续时间,G(·)是功放的非线性传递函数,W是离散傅里叶反变换矩阵:
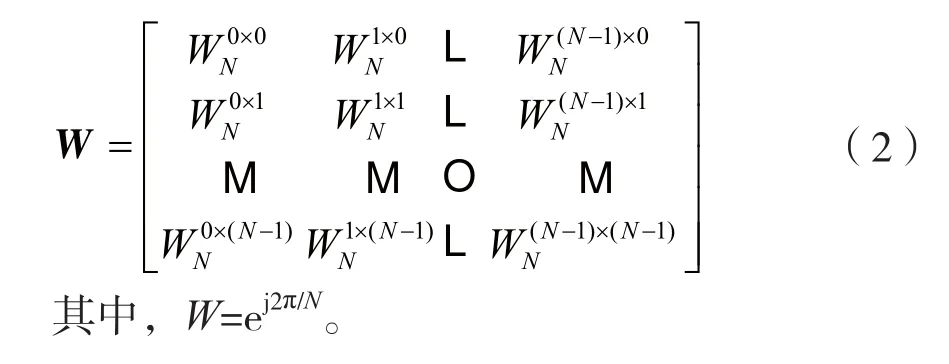
1.2 功放归一化模型
归一化的非线性功放传递函数模型可以表示为:
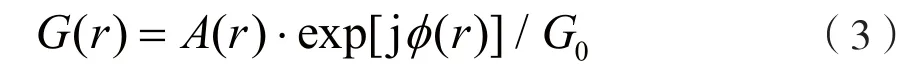
其中,A(r)是非线性功放的幅度对幅度(AMAM)响应;φ(r)是非线性功放的幅度对相位(AMPM)响应;G0是一个常数因子,使得G(r)的数学期望E[|G(r)|2]=1。
行波管功放(Travelling Wave Tube Amplifier,TWTA)和固态功放(Solid State Power Amplifier,SSPA)的AM-AM模型分别为[7]:

其中,αa,βa,υ,p是调节因子,由功放本身物理特性决定。
TWTA和SSPA的幅度对相位(AM-PM)模型分别为[7]:
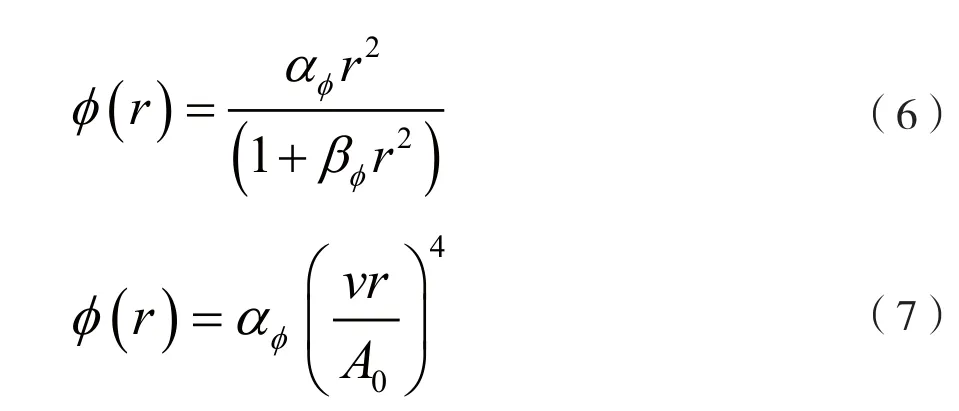
如果功放输入信号为非恒包络信号,功放的静态工作点就不能实现最大功率输出,即功率回退。功率回退有两种定义:输入功率回退(IBO)和输出功率回退(OBO)。
功放的输入功率回退定义为[7]:

其中,Pmax_in为最大允许的输入功率,Pi为当前的输入平均功率。
功放的输出功率回退定义为[7]:

其中,Pmax_out为输出功率最大值,Po为当前输出平均功率。IBO和OBO的关系,可以根据功放AM-AM表达式计算得出。
2 功放最佳静态工作点分析
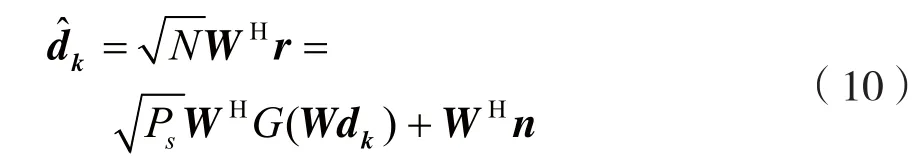
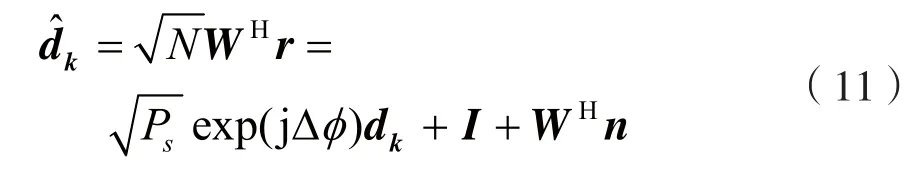
其中,Δφ是由于功放非线性带来的相位偏移,I是由于功放非线性带来的非线性噪声,WHn是加性白高斯噪声矢量。
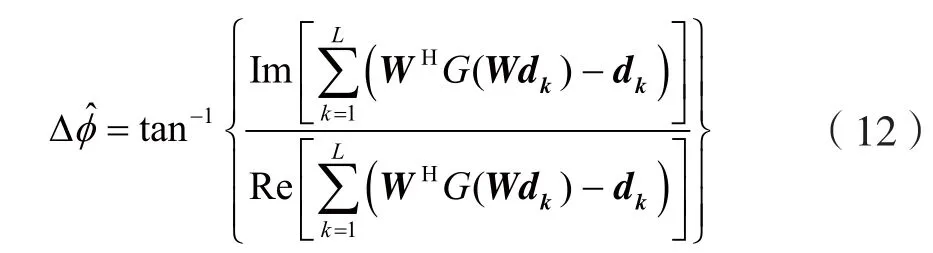
其中,Re[·]表示实部,Im[·]表示虚部,tan-1{·}是反正切函数。
在实际工程中,需要选择恰当的功放工作点。功率回退过多,线性度更好,却不能有效发挥功放的性能;功率回退过少,功放的有效输出功率变大,但解调性能却变差,需要折中权衡。
为了满足某个误码率指标,例如10-4,系统总体性能损失(Total Degradation,TD)定义为:

其中,SNR'是受非线性影响的链路要满足误码率指标对应的信噪比,SNR是理想链路要满足误码率指标对应的信噪比。使得TD最小的OBO,就是功放的最佳静态工作点。
3 仿真结果及分析
仿真设置子载波个数为256,M-QAM的调制阶数M=64,训练帧数L=1 000。TWTA功放参数为αa=1,βa=0.25,αφ=π/6,βφ=0.25;SSPA功放参数为:v=1,p=2,A0=1,αφ=π/3。
3.1 IBO和OBO关系仿真
根据式(5)﹑式(6)﹑式(8)﹑式(9),绘制出IBO和OBO曲线见图2。由于功放特性差异,同一输入IBO,对应了不同的输出OBO。

图2 IBO和OBO关系
3.2 星座图仿真
经过TWTA功放的64QAM星座图见图3。可以看出,TWTA功放带来了噪声和星座点的相位旋转。
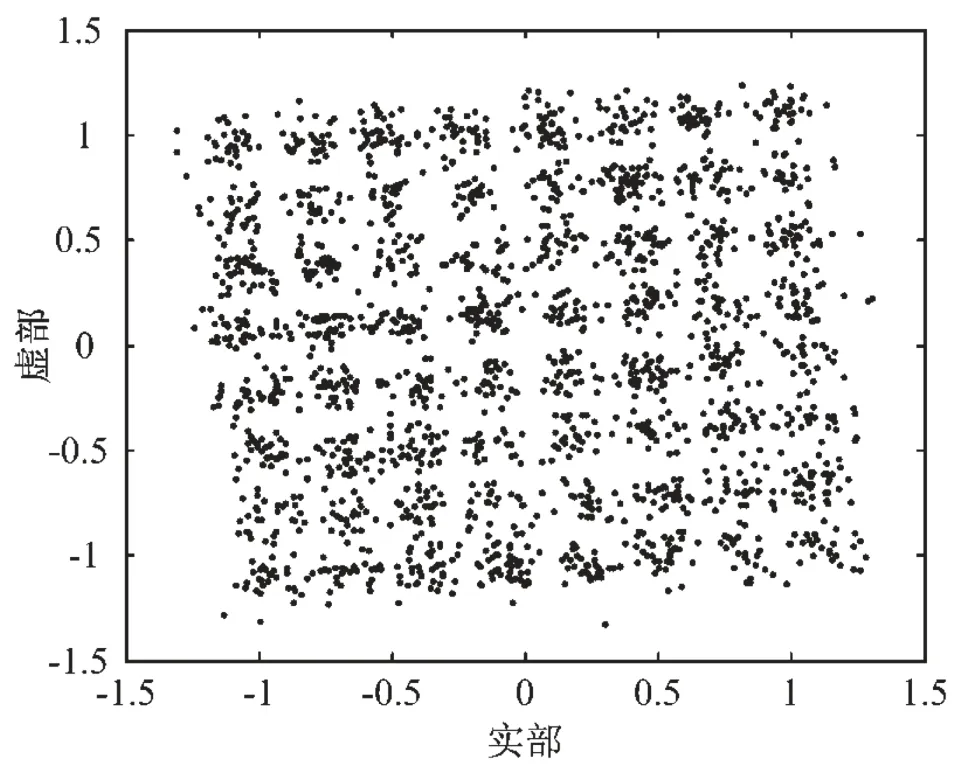
图3 经TWTA功放的64QAM星座(OBO=4.8 dB)
3.3 非线性噪声分析
OBO=4.3 dB时,SSPA功放带来的非线性噪声的概率密度函数见图4。与同方差的高斯概率密度相比,高斯概率密度的两边衰减更快。假如采用高斯建模的方法模拟非线性噪声,则其和实际仿真会有偏差。所选的误码率观察点越低(例如10-5),差别会越大。
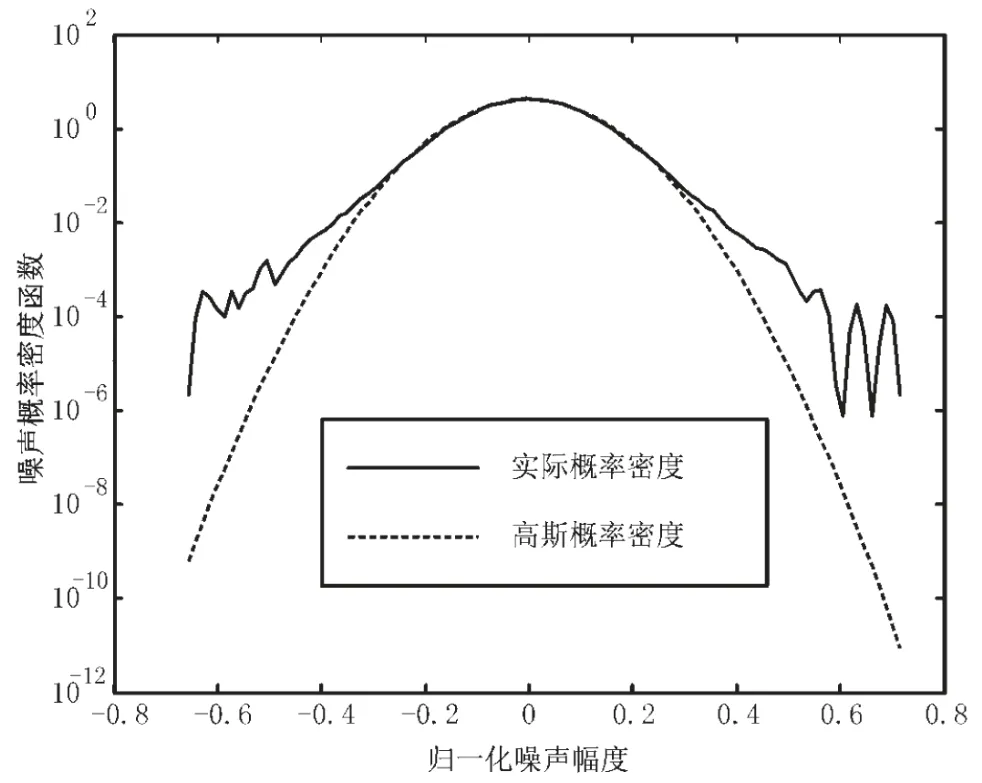
图4 OBO=4.3 dB,SSPA功放带来的非线性噪声概率密度函数
3.4 M-QAM OFDM性能仿真
不同SSPA功放输出功率回退条件下的64QAM误码率曲线,见图5。从图5可以看出,OBO越大,性能越好。在OBO=5.7 dB和6.1 dB时,随着比特信噪比Eb/N0的增大,出现了平层现象。这是由于功放带来的非线性噪声引起的。与理想64QAM在误码率10-4处相比,OBO为6.6 dB﹑7 dB时分别损失信噪比0.8 dB﹑3.4 dB。

图5 经过SSPA非线性功放的64QAM性能曲线
不同TWTA功放输出功率回退条件下的64QAM误码率曲线,见图6。从图6可以看出,OBO越大,性能越好。在OBO为6.1 dB时,随着比特信噪比Eb/N0的增大,出现了平层现象。这是由于功放带来的非线性噪声引起的。与理想64QAM在误码率10-4处相比,OBO为6.5 dB﹑7 dB﹑7.4 dB时分别损失信噪比4.9 dB﹑5 dB﹑7.5 dB。
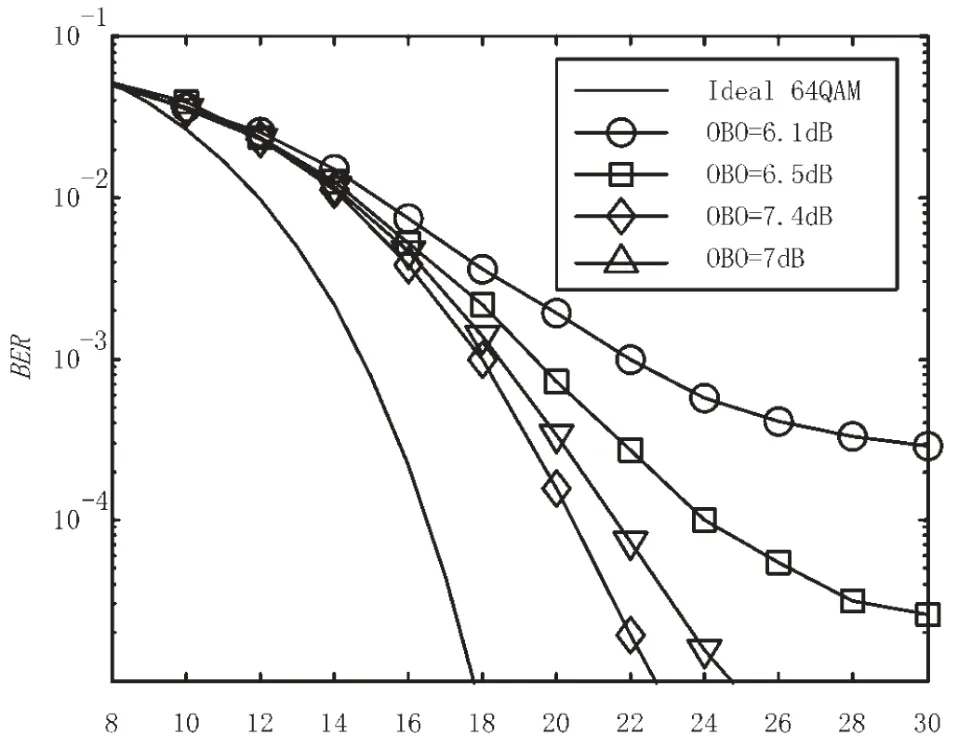
图6 经过TWTA非线性功放的64QAM性能曲线
按照式(13),不同功率回退OBO条件下的性能损失曲线见图7。可以看出,TWTA功放和SSPA功放都存在最佳的静态工作点,即OBO=6.9 dB (SSPA)和OBO=7.9 dB(TWTA),使得系统总体性能损失(TD)最小。可以发现,M-QAM OFDM系统中,即使OBO回退16 dB,也与理想功放相差2.6 dB。这是由于多载波OFDM对功放的线性度非常敏感造成的。
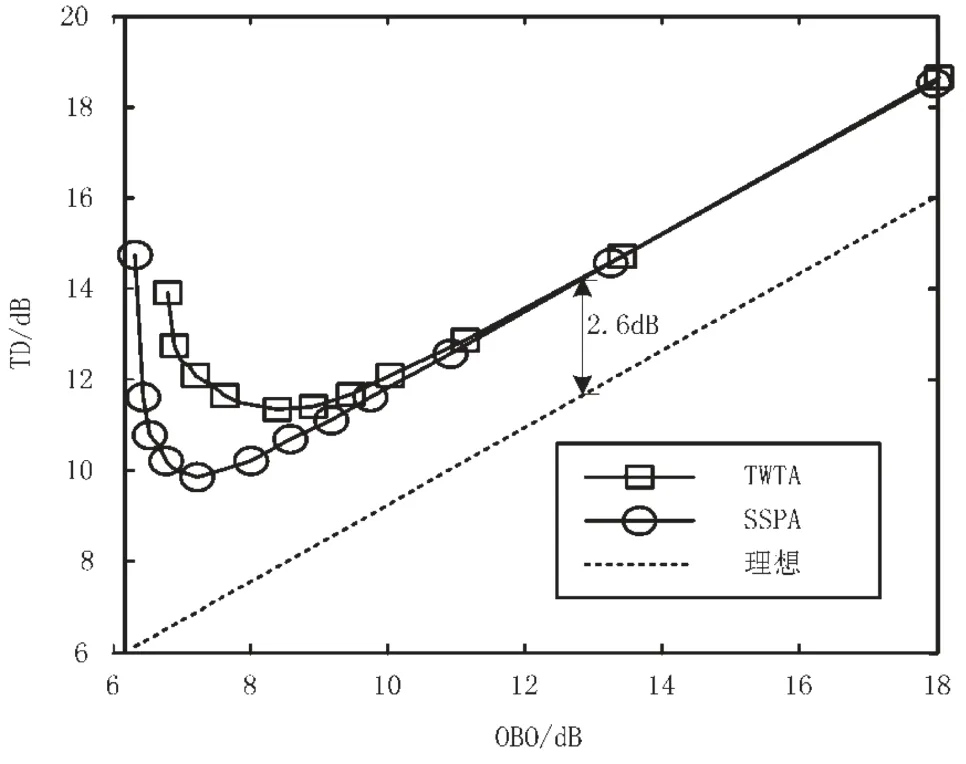
图7 不同功率回退下的系统总体性能损失曲线
4 结 语
本文仿真了功放非线性对M-QAM OFDM性能的影响。将非线性影响归结为两类:星座图旋转和非线性噪声。通过训练序列估计的方式,矫正星座图旋转角度;仿真了非线性噪声的概率密度函数,并与高斯近似的概率密度函数做对比;给出了选择功放静态工作点的方法,为相关工程应用提供参考。
[1] 李丹,柯峰.高速移动环境下基于OFDM的LTE系统ICI消除技术综述[J].重庆邮电大学学报:自然科学版,2013,25(03):292-299.
LI Dan,KE Feng.CI mitigation Techniques for OFDM based LTE System over Highly Mobile Environment:a Su rvey [J].Jou rnal of Chongqing University of Posts and Telecommunications(Natural Science Edition),2013,25(03):292-299.
[2] 张克,李洋,刘阳等.RS-Turbo级联码在DVB-T信道中的仿真分析[J].通信技术,2008,9(41):44-46.
ZHANG Ke,LI Yang,LIU Yang,et.al.Simulation Analysis of RS-Turbo Concatenated Code over Dvb-t Channel[J]. Communications Technology,2008,9(41):44-46.
[3] 刘鲲.OFDM电力线载波远程智能抄表技术[J].电力系统通信,2009,30(204):9-13.
LIU Kun.PLC Smart Metering based on OFDM[J]. Te lecomm un ica tion s fo r E lec tr ic Pow e r System,2009,30(204):9-13.
[4] 李光球.M R64QAM/OFDM传输系统中的非线性分析[J].上海交通大学学报,1999,33(01):32-35.
LI Guang-qiu.Nonlinear Analysis of MR 64QAM OFDMTransmission System[J].Journal of Shanghai Jiaotong University,1999,33(01):32-35.
[5] 康弘俊,许从方.基于脉冲成形技术降低OFDM峰均比[J].通信技术,2012,45(02):35-38.
KANG Hong-jun,XU Cong-fang.Reduction of OFDM PAPR based on Pulse Shaping[J].Communications Technology,2012,45(02):35-38.
[6] 郑紫微,杨知行,朱义胜等.存在非线性失真和相位噪声影响的CP-OFDM与TDS-OFDM数字电视地面广播传输系统的性能分析[J].电子学报,2004,32(10):1625-1629.
ZHENG Zi-wei,YANG Zhi-xing,ZHU Yi-sheng,et al.Performance Analysis of the CP-OFDM-based and the TDS-OFDM-based Digital Television Terrestrial Broadcasting Transmission Systems in the Presence of Nonlinear Distortions and Phase Noise[J].Acta Electronica Sinica,2004,32(10):1625-1629.
[7] ELENA COSTA,SILVANO PUPOLIN.M-QAM-OFDM System Performance in the Presence of a Nonlinear Amplifier and Phase Noise[J].IEEE Transactions On Comm unications,2002,50(03):462-472.
Analysis on am p lifier nonlinearity of M-QAM m odulated OFDM system
FAN Xiao-qin, WANG Ju, JI Lei
(The 30th Research Institute of CETC, Chengdu Sichuan 610041, China)
PAPR (Peak to Average Power Ratio) of M-QAM modulated OFDM is usually high, and the nonlinearity of amplifier may cause the performance degradation. In this paper, the impact of amplifier nonlinearity on M-QAM modulated OFDM is discussed. The impact of nonlinearity is summarized as two types, i.e., constellation rotation and nonlinear noise, the constellation rotation may be estimated with training sequence, while the statistics of nonlinear noise and BER (Bit Error Ratio) curves with different static operating point of amplifier are simulated. And finally a trade-off of between the output power and the SNR loss is given. In engineering applications, both the signal-to-noise ratio loss and total performance loss can be calculated quickly in accordance with the method when the characteristic curve and the modulation parameters are known, and the optimal static operating point of the power amplifier could thus be determined.
M-QAM OFDM; power amplifier; the optimum static operating point; constellation

TN911.22
A
1002-0802(2016)-11-1552-05
10.3969/j.issn.1002-0802.2016.11.026
樊小琴(1982—),女,硕士,高级工程师,主要研究方向为通信与信号处理;
王 菊(1986—),女,硕士,工程师,主要研究方向为通信与信号处理;
吉 磊(1984—),男,硕士,工程师,主要研究方向为通信与信号处理。
2016-07-09;
2016-10-08 Received date:2016-07-09;Revised date:2016-10-08
