有序探寻优化思维
2017-01-13谢辉兰
谢辉兰
《包装的学问》是北师大版《数学》五年级下册“数学好玩”领域的内容,如何遵循学生的认知规律,引导学生有序探寻,让学生经历多样化的包装方法,体验策略的多样化,然后有效对比,发现 “重叠面积越大越节约包装纸”的规律,发展优化思想呢?
一、活用经验
一盒糖果的成功包装是后续包装多盒的基础。教学中,笔者创设问题情境:儿童节快到了,班上的玲玲同学想用一张精美的包装纸把一盒糖果(长是20厘米、宽是15厘米、高是5厘米)包装起来,当作神秘的礼物送给“手拉手”栏目线下的一个小朋友,你能帮忙算算需要多少包装纸吗?有学生根据经验算出该长方体的表面积是(20×15+20×5+15×5)×2=950平方厘米,得出需要950平方厘米的包装纸。这时有学生提出质疑,因为实际包装过程中会产生接头,所用的包装纸的表面积会大于950平方厘米。经过讨论,师生达成一致意见:为方便计算,所需包装纸的面积一律按长方体的表面积计算,且根据同一长方体中各个面的面积大小,将三个面依次命名为大面(20×15)、中面(20×5)、小面(15×5)。
此处,教师有意识将解决生活中需要多少包装纸与长方体的表面积联系起来,让学生意识到所用包装纸的实际面积比糖果盒的表面积大,在接口处不计的前提下,包装纸的面积就是糖果盒的表面积。这不仅为探寻怎样包装最节约包装纸扫清了认知障碍,而且为后面交流包装方式(重叠了哪个面)做了必要的铺垫。
二、操作演算
通过以上铺垫,笔者引导学生继续思考:如果将这样的两盒糖果包成一包(接口处不计),怎样包装才能节约包装纸?学生运用学具,分组合作探究两盒糖果包成一包的包装方法,发现共有三种方法:大面重叠;中面重叠;小面重叠。笔者让学生猜想:哪种方法最节约包装纸呢?为什么?学生指出大面重叠最节约包装纸,因为这种方法被遮住的面积最大。如何验证这一猜想呢?学生想到了计算两盒叠放后长方体的表面积,要么先求出每个新的长方体的长、宽、高,再计算出它的表面积;要么利用露在外面的面求出它的表面积,比如大面重叠,露在外面的就有4个中面,4个小面和2个大面,把这些面的面积加起来就是大面重叠后新的长方体的表面积;要么用两个长方体的表面积之和减去两个重叠面的面积之和。计算过程中,学生发现第三种算法最简便,并列式计算出大面重叠后新长方体的表面积是1300平方厘米(950×2-20×15×2);中面重叠是1700平方厘米(950×2-20×5×2);小面重叠是1750平方厘米(950×2-15×5×2)。计算比较后,学生发现确实是大面重叠最节省包装纸。究其原因,是因为大面重叠减去的面积多,剩下的面积少,而小面重叠减去的面积少,剩下的面积多,所以大面重叠最节约包装纸。要知道怎样最节约包装纸,只要看重叠的面积。
面对三种包装策略,从节约包装纸的角度来寻求最优的方法,需要学生凭借经验合理猜测,然后通过计算进行验证对比。而计算的方法是多样化的,教师引导学生侧重关注了“总面积减去重叠面积”这种方法,采用追问的方式引导学生分析计算结果,然后反观其过程,使学生聚焦重叠面积的大小与表面积大小之间的关系,体验到重叠大面最节约包装纸,由表及里地把学生的思维引向深入,优化了思考问题的途径,发展了推理能力和反思能力,为后续探究道路指明了方向。
三、破除定势
学生知道包装两盒重叠大面最节约后,笔者让学生思考,包装三盒怎样最节约呢?根据先前的经验,刚开始学生发现共有三种方法:4个大面重叠、4个中面重叠和4个小面重叠,其中,4个大面重叠最节约包装纸。之后,为了让学生意识到两个中面之和与一个大面相等的情况下还可以有另外包装的方式,于是拿出事先准备好的大面(20×10)、中面(20×5)、小面(10×5)相同的3个盒子,询问学生除了大家想到三种方式,还可以怎样摆?学生很快意识到还可以先重叠其中2个大面,再让另1个大面与2个中面重合的包装方式。这样看起来就重叠了3个大面,2个中面,不同于前三种包装方式,那么是不是这种方法比前面三种方法更节约包装纸呢?再让学生想一想、算一算,学生在观察、思考、演算中发现2个中面之和与1个大面正好重合,相当于还是重叠了4个大面。这样,大面重叠最节约包装纸的经验对于包装盒个数多的情况不是唯一的,有些情况下还可能不成立。
把重叠大面最节约包装纸的经验和方法迁移到解决三个糖果盒包一包的问题上来,具有一定的可取性,但也是片面的。如何让学生深刻认识到重叠面积越大越节约包装纸而不是重叠大面最节约包装纸呢?教师设计了三个特殊包装盒包成一包,演示了常见的三种方式和特殊的包装方式(重叠3个大面,2个中面),打破了学生既有的“重叠大面最节约包装纸”的思维定势,让学生不断调整思路,逐层深入,优化方法,把握问题的核心,关注重叠面积的大小。
四、分析推理
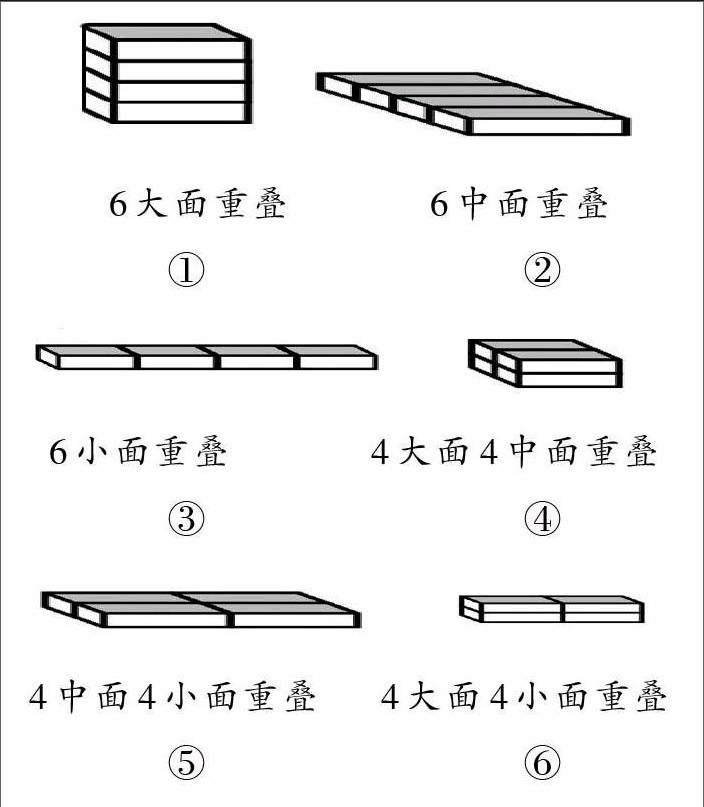
在探讨四盒糖果的包装方案时,学生分析出六种方案(如下图):①6个大面重叠;②6个中面重叠;③6个小面重叠;④4个大面4个中面重叠;⑤4个中面4个小面重叠;⑥4个大面4个小面重叠。
根据图示和先前经验,学生发现最先排除的是方案②③⑤⑥,方案1中重叠了6个大面,方案4中重叠了4个大面和4个中面,不好判断哪种方案更合理。经过分析,学生发现方案①和方案④中都有四个大面,只需比较剩下的2个大面和4个中面,最终可转化成比较1个大面和2个中面的面积大小。如果1个大面的面积大于2个中面的面积,那么方案①最佳;如果1个大面的面积等于2个中面的面积,这两种方案都可行;如果1个大面的面积小于2个中面的面积,那么方案④最佳。笔者让学生结合以上操作经验,谈谈自己在节约包装方面的体会。经过讨论,学生发现:重叠面积越大越节约包装纸,首先考虑大面的多次重叠,其次是重叠的面数尽量多。
(作者单位:宜都市实验小学)
