利用三次样条改进蚁群算法的无人机航路规划

程 琪，荆 涛，于志游

（中国民航大学航空自动化学院，天津 300300）

利用三次样条改进蚁群算法的无人机航路规划

程 琪，荆 涛，于志游

（中国民航大学航空自动化学院，天津 300300）

针对无人机在二维平面自动飞行中转弯角度过大、路径规划困难的问题，研究了蚁群算法在复杂环境下航路规划中的应用，利用链接图简洁的特点建立空间模型，对无人机的飞行环境和航迹代价进行了描述，并结合三次样条插值函数与蚁群算法，提出了改进蚁群算法，对无人机飞行路径进行优化，并给出算法软件流程；利用MATLAB进行了仿真实验，得出了最优的航路，算法具有较好的稳定性和鲁棒性，对轨迹中不可飞的尖角进行了平滑处理，使得航路为曲线轨迹，满足无人机工作的性能要求，减少无人机在飞行中的代价损耗，验证了该优化算法在无人机航路规划中的可行性。

蚁群算法；三次样条插值函数；航路规划；链接图；Dijkstra算法

0 引言

随着物流业的快速发展，无人机低成本和三维飞行能力使其在货物投递方面优于人工投递，其中无人机在已知固定区域进行最优航路规划（Path Planning）是无人机任务规划中的重要内容。

目前较常见的航路规划算法有Dijkstra算法，A*算法、人工势场法等，其中Dijkstra算法是一种经典的单源点的路径规划算法，具有简单便捷的特点，易于无人机软件实现。A*算法可以保证距离上的最短，但是无法兼顾例如转弯半径等其他性能指标。蚁群算法（Ant Algorithm）是一种基于种群寻优的概率搜索算法，是众多蚂蚁协同搜寻后得出一条最优路径，蚁群算法正反馈的特点使其具有较好的鲁棒性和全局规划能力。三次样条插值函数具有二阶连续导数，可以解决如飞机外形的理论模型、舶体放样等型值线等要求的二阶光滑度［1］，在路径规划中可以作去除尖角处理。

无人机路径规划由于约束条件的复杂性和任务的风险代价而成为无人机飞行任务中的难题，目前国内外学者大多采用图论将复杂的环境用几何图形构建的模型来进行研究，但基于几何图形的路径存在折角或在路径中有不可飞的尖角，不满足无人机本身的机动性能。文献［2］在路径的折角处利用圆弧拟合，通过构造角平分线为辅助线，以固定点为圆心作弧，与折角的两边相切，实现圆滑处理，该算法简单但缺乏整体性，在折角较大的地方很难实现较好的拟合；文献［3］中利用MATLAB的样条工具箱和最优化工具箱，取相邻路径段中点为两边节点，通过序列二次规划求得中点节点的最优解，连接3个节点绘制曲线来拟合路径中的尖角，但构造二次规划的函数过于复杂，求解过程繁琐。本文在文献［2］和文献［3］的基础上，针对无人机投递中对象区域固定，通过构建链接图（MAKLINK空间模型），提出了一种将三次样条插值函数和蚁群算法相结合的改进算法。在Dijkstra算法构建的粗略最短路径基础上，利用蚁群算法将空间模型中的航路点离散化，指引搜索下一段航路，并通过追赶法求解方程组，整理出三次样条插值函数，将蚁群搜索出的航路点带入三次样条插值函数重新求解，绘制曲线，将航路中的尖角平滑，从而满足无人机飞行的转弯半径要求，最后在仿真实验中证明了改进蚁群算法具有较好的可行性。

1 飞行环境描述

1.1 建立MAKLINK图

无人机在执行空中投递任务时，飞行高度可近似为保持不变，认为无人机在飞行过程中保持恒速飞行。定义环境中横向X方向和纵向Y方向，并以一定单位量m进行等量划分，则可以得到（X／m）×（Y／m）的网格图。在网格中标注固定区域的顶点坐标，并用链接线相连，就构成了威胁区域，为保证无人机能够成功完成飞行任务，需要在航路规划中规避威胁区域。以多边形的威胁区域为基准，将网格区域划分为N个包括威胁区域在内的凸多边形，相邻区域之间用链接线隔开，用迭代法计算出链接线的中点坐标。投递任务中设定飞行起点S、终点T和中途停留点P，依据设定点所属区域的划分，相同区域内的链接线中点之间相互连接，构成MAKLINK图，其中的链接线组成了可选航路段集合，各中点和设定点组成了可选航路点集合。在MAKLINK图中，起点S连接的第一个航路段规定无人机的初始航向，终点T连接的最后一个航路段规定无人机的终止航向。

1.2 航迹代价描述

由于飞行环境的多样性，无人机在完成飞行任务的过程中需要考虑不同因素对航迹优劣程度的影响［4］。根据威胁区域在MAKLINK图中的分布以及可选航路段的特征，可以将航迹规划的优劣程度用航迹代价来表征，航迹代价J［5］可分为受威胁区域影响的威胁代价Jthreat和受航路段距离影响的路程代价Jdist。

二维环境模型中的威胁区域均为多边形，无人机在飞行过程中距离威胁区域边界越近，受威胁的程度越大，威胁代价与航路段上的点到威胁区域边界的垂直距离d［（x，y），（m，n）］的成反比：

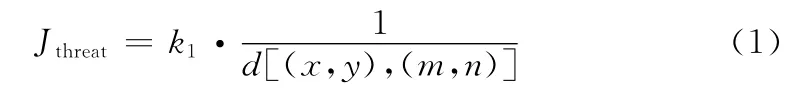
无人机在匀速飞行的过程中，会产生燃油消耗，随着飞行距离的增加，燃油消耗也相应地增加，因此路程代价与航路段的长度Li成正比：

综合考虑航路轨迹的优劣程度，航迹代价J表示为：

式中，k1和k2分别代表威胁代价和路程代价的权重，且k1＋k2＝1；M为航路段的数量，N为一条航路段上计算威胁代价的航路点的数量；在d（（x，y），（m，n））中，（x，y）为航路段上点的坐标，过（x，y）点作与航路段垂直的辅助线，（m，n）为辅助线与威胁区域边界的交点。

利用航迹代价将MAKLINK图构造成带权无向网络图G＝（V，E，W），其中V为所有航路点的集合，E为每段航路的集合，W为每段航路的权值：

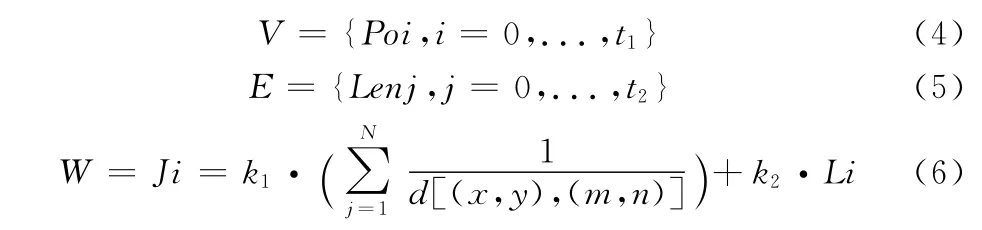
2 Dijkstra算法规划粗略路径

在飞行区域的链接图中利用Dijkstra算法找出粗略的最短路径［6］，Dijkstra算法基本步骤如下：

1）在带权无向网络图中，把集合V分为集合S和集合T，S存放已标记点，T存放未标记点。

2）初始化时，S中元素为s，T中元素为s以外的所有点。

3）源点s到集合T中的所有航路点的最小权值总和记录在数组dist中，i为数组dist中最小值dist［i］的航路点，把点i从集合T中取出放入集合S中。

4）更新数组dist中的值。

5）当所有的航路点都被标记时，即S中包含所有的航路点时算法结束，否则继续步骤3）。当算法结束时，可以求得一条航迹代价最小的粗略最短路径。

3 改进蚁群算法

利用经典蚁群算法对粗略最短路径进行优化，通过改变航路点的分布，搜索出新的航路点，并通过三次样条插值函数对新的航路点重新求解，绘制曲线对折线段的尖角进行平滑处理。

3.1 基本蚁群算法

已知航路点对应的链接线为leni（i＝1，2，...，d），对leni按照一定的比例系数k进行分割，则增加了可能航路点的数量，便于Pi在leni上进行局部调整，从而得到新的航路点：

对各段链接线进行离散化处理，即进行固定距离划分［7］，划分长度为ζ，每条链接线的划分数为：

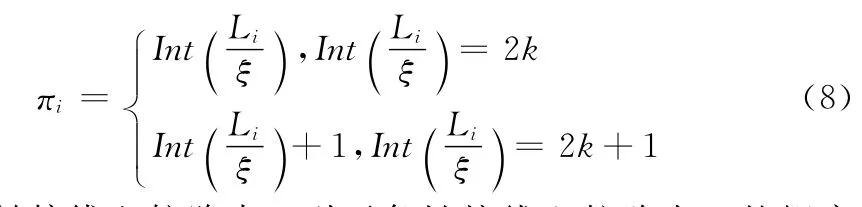
当前链接线上航路点i到下条链接线上航路点j的概率Pi，j（t）［8］为：

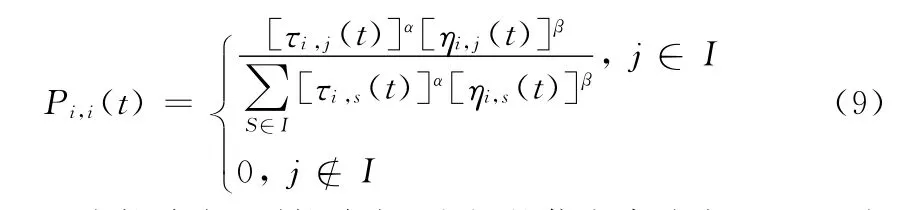
式中，τi，j（t）为航路点i到航路点j之间的信息素浓度；ηi，j（t）为启发函数，表示蚂蚁从航路点i转移到航路点j的期望程度，α表示信息素浓度对蚂蚁选择路径所起的作用，β为启发函数重要程度因子，其值越大，表示蚂蚁会以较大的概率转移到距离短的航路点。I表示蚂蚁待访问航路点的集合。

每一次选择节点后，对信息素进行更新：

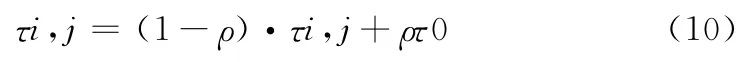
其中0≤ρ≤1，τ0为信息素的初始值。当一次完整的搜寻结束，同样要对信息素进行更新，公式同上，将τ0替换为1／Lmin，其中Lmin为最短路径值。

3.2 三次样条插值

定义被插函数y＝f（x），自变量范围x∈［a，b］，取n个节点xi∈［a，b］（i＝1，2，...，n），f（x）在这n个节点上对应的函数值为yi（i＝1，2，...，n）。若存在一个多项式函数P（x）使得P（x）＝yi，其中i＝1，2，...，d，则P （x）成为这n个节点xi的插值函数。若P（x）满足在区间［a，b］内有二阶导数，并且在每个相邻节点的区间［xi，xi＋1］（i＝1，2，...，n－1）内P（x）为三次多项式，则称P （x）为（xi，yi）的三次样条插值函数。

3.3 三次样条改进蚁群算法

3.3.1 分段三次插值［9］

函数在节点处的导数已知时，利用分段插值可写出每个相邻节点区间［xi，xi＋1］（i＝1，2，...，n－1）的样条函数：

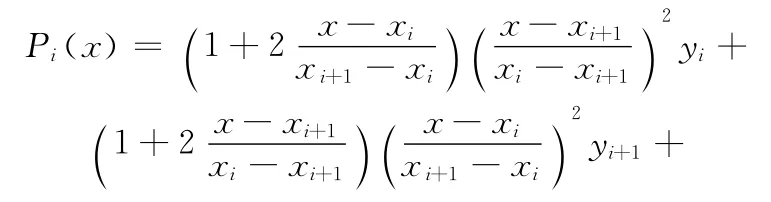
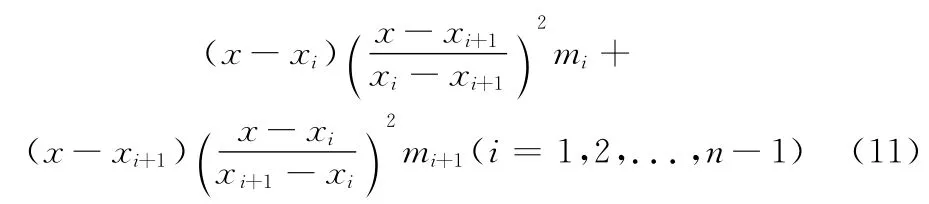
式中，mi为节点处的一阶导数值。

3.3.2 构造方程组

三次样条插值函数满足在规定区间内具有连续二阶导数，因此对P（x）求二阶导数可得到P″i（x），并使得，通过整理对节点建立方程组：

通过计算，可求出一组mi（i＝1，2，...，d），从而根据mi确定三次样条插值函数。

3.3.3 平滑曲线

基本蚁群算法依据搜索概率Pi，j（t）确定了每条链接线上的当前航路点POINT（λ），选取从起点S到终点T之间的所有航路段中点Z（λ＋1），由Z（λ＋1，1）构成节点（xi，yi）的横坐标向量组，Z（λ＋1，2）构成节点（xi，yi）的纵坐标向量组，利用三次样条插值函数对路径重新构图，得到平滑曲线，实现路径最短化，又将航路中不可飞的尖角平滑处理，满足无人机的转弯机动性能。

3.3.4 改进蚁群算法

该算法流程如图1所示。

图1 改进蚁群算法流程图

4 仿真实验

以校园内建筑平面图为例，对无人机执行任务来说，威胁区域主要是教学楼所在区域，依据此方法，在校园内某一范围内的地形平面图中，假设平面中教学楼为多边形区域，取一定高度H下的等高二维平面图，可得无人机飞行环境的威胁分布图。在Matlab2013中构造MAKLINK图，对算法进行仿真实验，试验中对经典蚁群算法的参数选择如下：

1）每条链路均离散化为10个小路段；

2）蚂蚁数量m＝10，循环次数为500次。

经典蚁群算法对粗略的最短路径进行优化，随着蚂蚁循环次数的增加，航路路径值和航迹代价值逐渐减小，优化路径如图2所示。图2中基本蚁群算法搜索出的最优航路和Dijkstra算法的粗略航路可看出明显对比。

图2 基本蚁群算法的优化航路

改进蚁群算法的程序包括参数初始化、蚁群搜索、信息素更新、追赶法求解方程组、绘制路径图等5个部分，将基本蚁群算法搜索出的新的航路点带入三次样条插值函数进行重新求解，通过增加区间节点数量，绘制出新的航路路径，如图3所示，图中标准的路径分别为Dijkstra算法的粗略航路、基本蚁群算法搜索出的航路以及三次样条插值函数改进的蚁群算法绘制出的最优航路。

图3 改进蚁群算法的最优航路

在关键航路点处的部分参数如表1所示，利用基本蚁群算法对粗略路径的路径值进行优化，航迹代价明显降低，部分航路段折角减小，经过改进蚁群算法的优化，航路段折角被曲线代替，轨迹得到平滑处理，且航迹代价保持最优状态。

可见改进后的蚁群算法在优化路径值的同时，解决了几何模型中存在路径尖角的问题，利用三次样条曲线平滑航路中的尖角，使无人机具有平滑的飞行轨迹，满足无人机本身在转弯时的机动性。

5 结论

无人机航路规划是在较复杂的飞行环境下，受多种约束条件限制的飞行任务规划，本文利用了MAKLINK图简洁明了的特点，通过以校园平面图为基础建立二维空间模型，对无人机的飞行环境进行描述，并定义了无人机在飞行过程中的航迹代价。结合了三次样条插值函数和蚁群算法，提出改进蚁群算法，利用蚁群算法的随机搜索的特点对飞行模型中的航路点进行离散化，使得蚁群能够进行全局搜索，也保证航路轨迹的最优和稳定性，并利用三次样条插值函数对航路点坐标重新取值，增加区间内节点数量，进行曲线绘制，对航路中不可飞的尖角进行平滑处理。从MATLAB仿真实验的结果来看，该方法稳定性好，航路轨迹较为平滑，各个航路点的转弯半径满足无人机的性能要求，减少无人机在飞行中的代价损耗，在最短的航程条件下完成飞行任务，对今后无人机航路规划以及其他二维空间路径规划提供参考。

［1］张德丰，等.MATLAB数值分析与应用［M］.北京：国防工业出版社，2009.

［2］曾 佳，申功璋，等.一种无人机平滑飞行轨迹规划方法［J］.系统仿真学报，2008，20：470-473.

［3］符小卫，高晓光，等.一种无人机路径规划算法研究［J］.系统仿真学报，2004，16（1）：20-21.

［4］华珊珊.无人机航路自动规划优化方法研究与仿真［J］.计算机仿真，2013，30（4）：45-48.

［5］李 猛，王道波，柏婷婷，等.基于蚁群优化算法和人工势场的无人机航迹规划［J］.应用科学学报，2012，30（2）：216.

［6］李元臣，刘维群.基于Dijkstra算法的网络最短路径分析 ［J］.微计算机应用，2004，25（3）：295-298.

［7］张美玉，黄 翰，郝志峰，等.基于蚁群算法的机器人路径规划［J］.计算机工程与应用，2005，41（9）：34-37.

［8］Glabowski M，Musznicki B，Nowak P，et al.An algorithm for finding shortest path tree using ant colony optimization metaheuristic ［J］.Advances in Intelligent Systems and Computing，2014，233：317-326.

［9］马昌凤.现代数值分析［M］.北京：国防工业出版社，2013.

［10］Khanmohammadi S，Zarrin R S.Intelligent path planning for rescue robot［J］.World Academy of Science，Engineering and Technology，2011，5（7）：607-612.

［11］Sullivan T A，Van J D.Multi-objective，multidomain genetic optimization of a hydraulic rescue spreader［J］.Mechanism and Machine Theory，2014，80：35-51.

UAV Path Planning Based on Ant Colony Optimization Improved by Cubic Spline

Cheng Qi，Jing Tao，Yu Zhiyo u

（College of Aeronautical Automation，Civil Aviation University of China，Tianjin 300300，China）

Focus on issues as the sharp of turning angle and difficulty of path planning in Automatic UAV flight in the two－dimensional plane，the paper studies the ant colony algorithm in a complex environment of UAV route planning，and establishes a space model to describe the flight environment of UAV in the use of the MAKLINK graph for the concise characteristics.The cost of the flight environment and track the UAV has been described in conjunction with cubic spline interpolation function and ant colony algorithm to optimize the UAV flight path，and algorithm software flow is shown.The optimal route which has better stability and robustness by using MATLAB simulation experiments is got，and the track route is relatively smooth，turning angle of each waypoint can meet the performance requirements of UAV，the cost of the UAV fighting is reduced corresponding，it is verified that the optimization algorithm of UAV route planning is feasible.

ant colony algorithm；Cubic spline interpolation function；path planning；MAKLINK Graph；Dijkstra algorithm

1671-4598（2016）08-0272-03

10.16526／j.cnki.11－4762／tp.2016.08.074

：TP18

：A

2016-02-29；

：2016-03-27。

国家自然科学基金（61405246）；天津市创新创业项目（201510059084）。

程 琪（1994-），男，江苏宿迁人，大学生，主要从事电气工程及其自动化方向的研究。