显微散焦粒子识别与追踪测速

赵攀杰，王昊利，汪 兵，韩威俊

（中国计量学院计量测试工程学院，杭州 310018）

显微散焦粒子识别与追踪测速

赵攀杰，王昊利，汪 兵，韩威俊

（中国计量学院计量测试工程学院，杭州 310018）

根据三孔挡板散焦成像的原理，使用高速散焦显微粒子测速装置开展三维显微粒子追踪测速研究；在粒子散焦像识别的过程中利用了其对应三角模型相似的特点，通过散焦像斑灰度呈二维高斯分布特征计算其质心；在粒子三维位置测量算法分析的过程中选择了多达29颗的样品粒子，对29组不同深度的数据采用线性拟合的方式进行粒子深度方向的标定，并用二元多项式对870组数据拟合获得了关于粒子平面位置漂移的补偿函数；针对长直微通道内雷诺数Re分别为0.05和0.1的流场进行了验证性测量，采用20×0.4显微物镜，使用高速CMOS相机对直径为2μm的粒子进行追踪；结果显示，计算出的示踪粒子速度分布与数值仿真曲线吻合良好。

散焦成像；模型识别；粒子测速；三维追踪

0 引言

在实验流体力学研究中，二维粒子图像／追踪测速系统（PIV／PTV）只能对流体进行分层测量，获取两个共面的速度分量（2D－2C），此类系统难以针对复杂三维流场进行测量。为了突破该限制开展复杂流动三维三分量（3D－3C）测量已成为实验流体力学研究人员的主要目标，其关键在于确定粒子在深度方向的位置和速度。

目前已经出现若干三维测速技术，包括：体视技术［1］可以从两个视角获得粒子图像，并通过两个图像平面计算出的位移来重建速度分量；数字全息显微镜［2］是数字全息术在显微物镜中应用的结果。通过显微物镜放大后使用图像传感器记录散射光与非散射光干涉图样作为全息图，粒子的空间位置可通过全息图像进行数值重建；波前传感器［3］和散光粒子追踪测速［4］利用一个附加的柱面透镜取代光学向场透镜来创建一个变形成像系统；利用粒子衍射模式的散焦技术［5］是基于散焦粒子图像的衍射效应。散焦粒子图像构成的同心环结构，其大小随深度间隔不同而变化，从而确定粒子的深度位置坐标。此外，有一类散焦技术利用多孔挡板使同一颗粒子在成像平面上呈现多个像斑从而形成一种特定的图样。通过图样大小随其粒子深度变化的相关关系便可计算出粒子的深度位置。这一散焦的概念由Willert和Gharib［6］首次提出，通过在图像传感器与被测实验对象之间嵌入三孔挡板的方式来成像。2006年，Yoon和Kim［7］首次将这种方法应用在了一个微尺度后台阶流动中。后来，Pereria等人［8］基于此技术而设计了一个高速三维显微散焦粒子测速系统，并提出了一种标定方法作为复杂多元化显微镜系统的一个等效光学模型来简化计算。而Tien等人［9-10］在挡板的每个孔上放置了一个可过滤不同单色光的滤色片以便容易识别散焦图像，并将其从宏观扩展到微观流速测量的运用中。

本文利用已经搭建的一套高速散焦显微粒子图像测速装置，在粒子三维空间位置标定的过程中，通过挑选更多的粒子来对其相关的测量算法进行更深一步的分析与研究。并在此基础上，针对长直微通道内Poiseuille流进行了测量，将测量结果与数值仿真的速度廓线进行了比较，验证该实验系统针对流体不同深度速度测量的有效性。

1 散焦追踪测速装置

搭建的高速散焦Micro－PTV测速系统装置，主要包括德国LaVison显微系统、MEMRECAMHX－6型CMOS高速相机（最大帧频可达5000帧／秒）、连续激光器LIF－532－5（功率为5W）、三孔挡板、注射泵、微流控装置、计算机等。

在实验中通过注射泵控制微流控装置内流体的流速，并使用20×0.4倍的显微物镜对微流场中直径为2μm的示踪粒子进行观测。利用连续激光器发射的532nm的激光可使这种示踪粒子激发出610nm的荧光，这种图像信号经过La Vison显微光学系统处理后由CMOS高速相机进行采集，在计算机显示屏中显示示踪粒子的图像。为了能够获取示踪粒子的深度信息，在LaVison显微系统的显微物镜后面嵌入了一个三孔挡板。因此，示踪粒子发生散焦现象并形成3个光斑。设计的圆形三孔挡板上3个圆孔的直径均为2 mm，三小孔圆心所构成的正三角形的几何中心位于圆形挡板的中心轴线上，其对应的外接圆直径为4 mm。其中，三小孔的边缘厚度均只有0.1 mm，且距挡板边缘间的厚度是成线性分布的。

三孔挡板利用了散焦成像的原理，示踪粒子的荧光信号通过三孔挡板成像的光路系统原理图如图1所示。示踪粒子在深度方向上的位置不同，在CMOS高速相机成像平面所成的散焦像的像径（即正三角形构型的外接圆直径）大小是不同的。当示踪粒子位于参考平面上时，所成像聚焦成一个像点，可将其像径的大小视为零。而当示踪粒子分别位于z＞0和z＜0这两个方向且距参考平面等距离处，其对应的散焦图像的像径大小相同，但方向相反。因此散焦图像能够避免粒子在焦平面两侧的深度位置产生歧义。

图1 孔板散焦成像原理简图［11］

2 三维粒子位置测量算法

2.1 粒子散焦图像识别

在粒子深度的标定过程中，当荧光粒子聚焦时所成的图像如图2所示；当其发生散焦时，所成的图像如图3所示，每个荧光粒子对应的散焦图像均为3个圆斑。为了识别出荧光粒子对应的散焦图像，采用了Yoon等人［7］提出散焦图像所成三角形构型相似的理论，其相似度公式如下：

其中：向量（r1，r2，r3）为参考三角构型（以三孔挡板的3个小孔的圆心作为其顶点）三边的矢量，向量（c1，c2，c3）为荧光粒子散焦图像所成三角形构型三边的矢量。在荧光粒子散焦图像的识别过程中，如果S≥0.99，则可把正在检测中的3个圆斑当作荧光粒子对应的散焦图像。

从图3中可以看出，每个三角形顶点处的像斑就是荧光粒子对应的散焦图像。利用像斑灰度值呈二维高斯分布的特点，能方便求出像斑的质心。这里用（X1，Y1），（X2，Y2）和（X3，Y3）分别表示荧光粒子散焦图像3个圆像斑的质心，进而可计算出由3个质心所成三角构型外接圆的直径D和圆心（X，Y）（见图4）。

图2 荧光粒子聚焦成像

图3 荧光粒子散焦成像及其识别

图4 荧光粒子散焦成像三角构型

2.2 粒子位置标定与分析

在粒子所成散焦图像像径与其深度关系的标定过程中，被测粒子由之前实验所采用的11颗粒子［11］增加到了29颗，并将标定深度由z＝－40μm增加到了z＝－70μm。把粒子群聚焦时的位置定义为参考平面（即粒子深度z＝0处），从z＝－14μm处开始，每隔2μm就用CMOS相机记录一次粒子群的散焦图像，直到z＝－70μm为止。为了减少粒子像斑测量的误差，取每个特定深度处粒子群的200张散焦图片，以其平均像径作为此深度处粒子的像径，然后再通过线性拟合的方法对粒子的29对像径与深度进行处理。从图5（a）中可以看出，粒子像径与其对应的深度有比较好的线性关系。虽然在这次的测量中粒子的像径与深度关系中也呈现出了弱非线性的特征（见图5（b）），但其斜率ΔD／Δz随粒子深度在参考线附近（图中水平虚线）上下浮动，其均方根误差（RMS）只有0.071，这与Pereira等［12］的研究结论是相一致的。

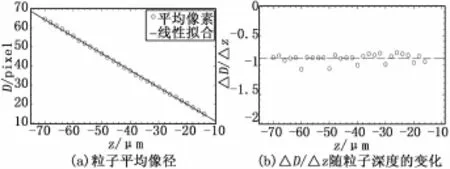
图5 粒子像经与深度图

因此，粒子像径D与深度z之间的关系式可表示为：

微通道内流体介质不同，粒子所对应的深度标定函数的系数就会发生变化。在减少重复标定工作方面，Yoon等人［13］提出了流体介质的折射率与其标定系数之间的关系式，如下：

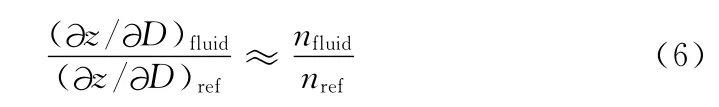
其中：nfluid和nref分别为实验溶液和参考流体的折射率，（∂z／∂D）fluid和（∂z／∂D）ref为这两种溶液对应的标定系数。

为了消除固定荧光粒子像平面中的位置（X，Y）随深度变化产生的漂移，获得补偿后粒子在水平面中的实际位置（x，y），这里，采用二元多项式补偿函数（见式（7）和式（8））［7］，通过最小二乘法对粒子群的870对三维坐标数据进行了拟合，获得了粒子在水平位置的补偿函数。

通过对任意一个选定的粒子使用水平位置x和y的补偿函数后，从图6（a）和（b）中可看到，粒子在水平面中的实际位置（x，y）获得了较好的改善，其大小随粒子深度在参考线（过粒子在z＝0处的水平位置（x，y）的虚线）附近轻微浮动。

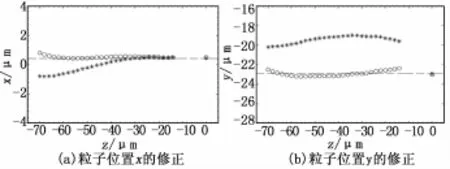
图6

图7给出的是粒子三维测量位置x／y／z的误差分析结果。从图中可以看出，29颗荧光粒子在x／y／z3个方向上的均方根误差（root mean square error，即RMSE）分别在参考线Rx＝0.1468μm、Ry＝0.1859μm和Rz＝0.4329μm附近上线变化。鉴于深度标定中的弱非线性趋势和粒子三维空间分辨率的不同等情况，粒子位置测量在z上的误差是在x与y的2～3倍。这与Pereira［12］及Yoon［13］等研究人员测量的实验结果是一致的。

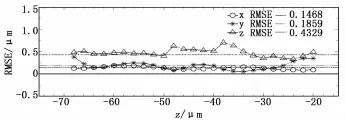
图7 粒子测量位置x／y／z误差分析

3 粒子追踪测速实验

在利用散焦粒子图像测速技术对长直微通道的速度场进行了测量，通道的截面为矩形和流向的结构见图8，其中长、宽及深度分别为5 mm、2 mm和50μm。由于宽深比达到了40 ∶1，因此可以近似地认为是两平板间流动。通道上端为玻璃板、下端由PDMS材料组成，两种材料具有良好的粘附性，制作简单，并在低速流下具有良好的密封效果。

被测流体为荧光粒子原溶液与去离子水按照1∶1 000体积比配制的水溶液，采用注射泵（格兰公司）进行驱动，流量分别设定为185.8μl／h和371.6μl／h，对应的雷诺数Re分别为0.05和0.1。测量点位于距长直微通道进口3 mm处附近，流场已经达到充分发展阶段，理论速度廓线为平板Poiseuille流。

图8 微通道矩形及流向结构截面视图

使用CMOS高速相机以1 000帧／秒的扫描速率对微通道内得流场进行拍摄，对其记录下来的序列图像通过维纳滤波去除噪声后，可得到较高质量的散焦图像。根据Yoon等人［7］提出散焦图像所成三角形构型相似的理论公式，能够识别出粒子对应的散焦图像。利用像点追踪开源软件Vide Spot Tracker v07.02对粒子3个散焦像斑进行追踪，根据像斑灰度值呈二维高斯分布的特点，求出像斑的质心，进而获得追踪粒子三像斑所构三角形外接圆的直径与圆心，即追踪粒子的散焦像径与质心。根据深度标定函数计算出粒子的实际深度位置，通过粒子水平方向上的补偿函数去对其质心位置进行修正，最终根据所追踪的示踪粒子轨迹获取粒子的速度矢量。

图9和图10分别给出了雷诺数分别为Re＝0.05和Re＝0.1的情况下，通道内部不同深度处的粒子轨迹。不同颜色代表了不同的深度，而不同深度处粒子在单位时间内移动的距离是不同的，且粒子距通道中心越近，其对应的速度越大。利用粒子轨迹分别计算出两个雷诺数下流场的速度廓线v1和v2，并分别与平板Poiseuille流的数值仿真结果进行比较，见图11和图12。可以看到实验值和数值仿真结果吻合良好，表明实验值满足平板Poiseuille流动。该实验结果验证了高速散焦Micro－PTV测速系统能够有效测量不同深度的流动速度，因此能够进一步推广至三维复杂流场的测量中。

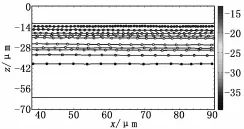
图9 Re＝0.05时长直微通道内的粒子轨迹

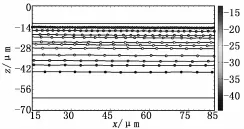
图10 Re＝0.1时长直微通道内的粒子轨迹

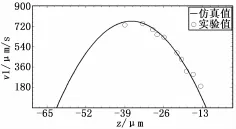
图11 Re＝0.05时粒子速度测量值与仿真值的比较

4 结束语

在已搭建的一套高速散焦显微粒子测速装置的基础上，通过增加粒子数并增大深度范围对粒子深度进行了标定，并用二元多项式对870组数据拟合计算出了关于粒子平面位置漂移的修正函数，完成了粒子三维空间位置测量算法分析与研究。针对长直微通道内流速的验证性测量中，分别对雷诺数Re＝0.05和Re＝0.1这两种不同的流速进行了测量，获取的示踪粒子速度分布与数值仿真曲线吻合良好。实验结果进一步验证了该系统装置在三维测速方面的可行性和追踪测速算法的有效性。

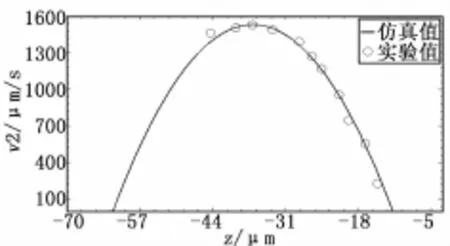
图12 Re＝0.1时粒子速度测量值与仿真值的比较

［1］Lindken R，Westerweel J，Wieneke B，et al.Stereoscopic microparticle image velocimetry［J］.Exp Fluids，2006，41（2）：161-171.

［2］Sheng J，Malkiel E，Katz J，et al.Digital holographic microscope for measuring three－dimensional particle distributions and motions ［J］.Appl.Opt，2006，45（16）：3893-3901.

［3］Angarita－Jaimes NC，McGhee E，Chennaoui M，et al.Wave front sensing for single view three－component three－dimensional flow velocimetry［J］.Exp Fluids.2006，41（6）：881-891.

［4］Cierpka C，Segura R，Hain R，et al.A simple single camera 3C3D velocity measurement technique without errors due to depth of correlation and spatial averaging for micro fluidics［J］.Meas.Sci.Technol.，2010，21（4）：045401.

［5］Park J S，Kihm K D.Three－dimensional micro－PTV using deconvolution microscopy［J］.Exp Fluids.2006，40（3）：491-499.

［6］Willert C，Gharib M.Three－dimensional particle imaging with a single camera［J］.Exp Fluids.1992，12：353-358.

［7］Yoon S Y，KimKC.3D particle position and 3D velocity field measurement in amicrovolume via the defocusing concept［J］.Meas Sci Technol.，2006，17（11）：2897-2905.

［8］Pereira F，Lu J，Castano－Graff E，et al.Microscale 3D flow mapping withμDDPIV［J］.Exp.Fluids，2007，42（4）：589-599.

［9］Tien WH，Kartes P，Yamasaki T，et al.A color coded back lighted defocusing digital particle image velocimetry system［J］.Exp Fluids，2008，44：1015-1026.

［10］Wei H，Tien D，Dabiri J，et al.Color－coded three－dimensional micro partilce tracking velocimetry and appl ication to micro backwardfacing step flows［J］.Exp.Fluids，2014，55：1684-1697.

［11］赵攀杰，王昊利.基于散焦的三维显微粒子追踪测速［J］.中国计量学院学报，2015，26（04）：428-434.

［12］Pereira F，Gharib M.Defocusing digital particle image velocimetry and three－dimensional characterization of two phase flows［J］.Meas Sci Technol.2002，13：683-694.

［13］Yoon S Y，Khim K D，Kim K C.Correlation of fluid refractive index with calibration coefficient for micro－defocusing digital particle image velocimetry［J］.Meas.Sci.Technology，2011，22：1-5.

Identification and Tracking About Three－dimensional Microscopic Defocusing Particle

Zhao Panjie，Wang Haoli，Wang Bing，Han Weijun

（College of Metrological Technology and Engineering，China Jiliang University，Hangzhou 310018，China）

According to the principle of a three－pinhole mask’s defocused imaging，a set of high－speed defocusing micro－PTV devices was employed for further research on the three－dimensional micro particle tracking velocimetry.The similar characteristics among particles’corresponding triangle models was used in the process of their defocusing images recognition，and the centroid of particle defocusing image spot was calculated by its gray in two－dimensional Gaussian distribution.As many as 29 sample particles were selected in the process of measurement algorithm analysis about particle’s three－dimensional position，and 29 different depth data were utilized for calibrating in the particles’depth direction with the method of linear fitting，and the drift compensation functions about the in－plane position of particle was acquired by quadratic polynomial fitting with 870 groups of data.A microscope objective lens of 20×0.4 and high speed CMOS camera were adopted to trace the particles of 2μm diameter in the verification measurement of a long straight micro－channel flow field whose Reynolds number were 0.05 and 0.1 respectively.The results showed that the particle velocity distribution calculated was in good agreement with the numerical simulation curve.

defocusing image；pattern recognition；particle velocity measurement；three－dimensional tracking

1671-4598（2016）08-0298-03

10.16526／j.cnki.11－4762／tp.2016.08.081

：TP317.4；0353.5

：A

2016-03-09；

：2016-03-24。

国家自然科学基金资助项目（11472261；11172287）。

赵攀杰（1988-），男，河南许昌人，硕士研究生，主要从事显微颗粒的可视化测量方向的研究。