冗余自由度工业机器人模糊自适应PID控制研究

葛 卓，罗庆生，梁冠豪

（北京理工大学机电学院，北京 100081）

冗余自由度工业机器人模糊自适应PID控制研究

葛 卓，罗庆生，梁冠豪

（北京理工大学机电学院，北京 100081）

为提高汽车生产中涂胶工序的工作效率和空间利用率，改善机器人避障性能，设计了一款具有7自由度的冗余度工业涂胶机器人，并对其控制方法开展研究；针对现有PID控制方法应用于非线性时变的多自由度多刚体串联式开链系统时，控制效果有限、难以达到系统精度要求等问题，基于传统PID控制和模糊自适应控制算法，提出了一种带有重力补偿的模糊自适应PID混合控制方法；该方法在对冗余度工业机器人进行动力学分析的基础上，基于牛顿－欧拉分析法建立了冗余度机器人动力学模型，基于动力学分析设计了带有重力补偿的模糊自适应参数整定PID控制策略，建立了控制器模型，通过Matlab仿真实验表明，具有模糊自适应参数整定PID控制较有重力补偿的传统PID控制具有更好的控制效果。

冗余自由度；工业机器人；动力学；模糊自适应

0 引言

汽车制造业是工业机器人应用较多的领域，多种类型、多个系列的工业机器人主要用于焊接、涂胶、喷漆等劳动强度大、工作环境差、重复动作多的加工过程。为了追求更为卓越的性能和外观，汽车涂胶的位置越来越变化多端。对有些特殊位置进行涂胶时，由于车窗框、工位中其他障碍物等的阻挡，普通的6自由度工业机器人无法同时实现涂胶所需要的位置和姿态，需要对车体的位置进行调整，或是需要增加改变末端姿态的节拍，导致涂胶工作无法一次性完成，大大降低了生产效率、降低了良品率。而关节空间维数大于任务空间维数的冗余自由度机器人，因其所特有的冗余特性，能够有效地解决这类问题。为了满足产业界对更高性能的工业机器人的需求，本文以一款经ABBIRB 1410工业机器人改造的7自由度涂胶机器人为研究对象，针对该冗余自由度机器人的动力学和控制问题开展研究。

传统的PID控制方法因为其控制简单易于实现，已经广泛应用于机器人、工业制造等控制领域。但由经典控制理论可知，PID控制方法面对非线性被控对象时，在整个控制区间内很难找到最佳PID参数；模糊控制器可以补偿系统中非线性因素的影响，获得良好的动态特性，但是难以消除静态误差［1］。随着智能控制理论的发展，先进的智能PID控制策略相继被提出，为复杂动态不确定机器人系统的控制提供了新的途径［2 5］。例如，任国华等针对移动机器人提出了一种多项式PD控制策略，通过Lyapunov直接法证明了闭环系统的全局稳定性［6］。胡克满针对六自由度喷涂机器人的位置控制问题，提出了一种基于BP神经网络的自适应PID控制策略，获得了较好的控制性能和应对参数变化的鲁棒性［7］。

本文将基于传统PID控制与模糊自适应控制算法的混合控制方法，在对冗余自由度工业机器人进行动力学建模的基础上，研究带有重力补偿的模糊PID控制方法，旨在探究适用于冗余自由度工业涂胶机器人这类非线性时变的多自由度多刚体串联式开链系统的控制方法，以提高系统精度，获得更佳鲁棒性和更好的控制效果。

1 冗余度涂胶机器人动力学模型

在实际中对机械臂进行控制时，人们对机械臂各关节的驱动力矩感兴趣。而对机械臂的逆动力学分析有助于构建机械臂关节期望的角位移、角速度、角加速度与关节所需驱动力矩之间的数学关系。因此，在对多刚体系统进行动力学分析时，构建系统的动力学方程是必由之路。目前，在常见的动力学分析方法中，主要有拉格朗日分析法与牛顿－欧拉分析法。根据在O.Khatib［8-9］的两篇文章表明牛顿－欧拉分析法的计算量相对较小。因此本文采用牛顿－欧拉分析法进行动力学分析。对单个机械臂连杆的力平衡分析，可以得出由关节运动计算转动型关节力矩的完整迭代算法，其由两部分组成。以第i根杆为例（i＝1，2，3，…，7），迭代算法如下：

1）从连杆1向连杆7顺序迭代计算连杆的速度和加速度；

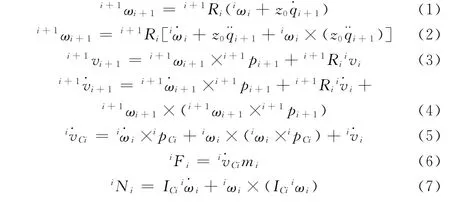
2）从连杆7向连杆1倒序迭代计算连杆间的相互作用力和力矩以及关节驱动力矩。

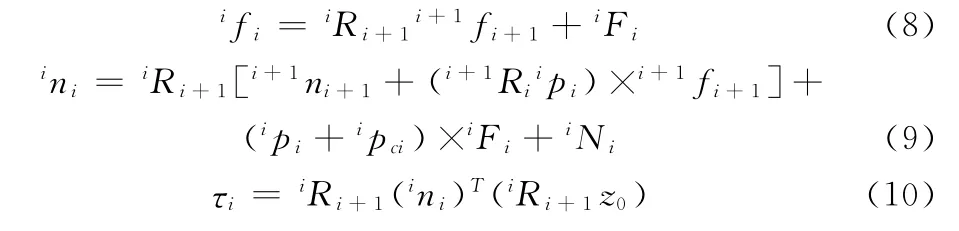
上述式中，i＋1Ri为坐标系｛i｝到坐标系｛i＋1｝的旋转矩阵；iωi和为连杆i在关节坐标系｛i｝下的角速度与角加速度；z0为任意坐标系下z轴单位矢量z0＝［001］；qi＋1，˙和¨qi＋1为关节i＋1在基坐标系下的角位移，角速度与角加速度；ivi和i˙vi为连杆i在坐标系｛i｝下的平移速度与平移加速度；为连杆i在坐标系｛i｝下的平移加速度；ipci为连杆i的质心在坐标系｛i｝下的表示；ipi为坐标系｛i－1｝原点到坐标系｛i｝原点的距离在坐标系｛i｝下的表示；iFi和ifi为作用在连杆i质心上的外力，连杆i－1作用在连杆i上的内力在坐标系｛i｝下的表示；iNi和ini为作用在连杆i上的外力矩，连杆i－1作用在连杆i上的内力矩在坐标系｛i｝下的表示；ICi为连杆i相对于其质心的转动惯量阵；τi为关节i产生的驱动力矩。

通过牛顿－欧拉分析法对冗余度涂胶机器人的分析，可以得到关于整个机械臂7个关节之间的力平衡方程组，化简以后，可以得到统一形式的动力学模型：

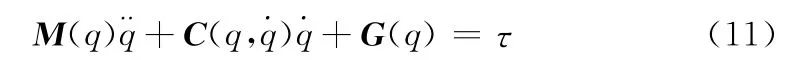
等式左侧，M（q）是冗余度涂胶机器人的7×7惯性张量矩阵，是该机械臂的科里奥利力和离心力7×7矩阵，G（q）则是一个表示该机械臂的重力项的7×1向量，而在等式右侧，τ是机械臂7个关节的驱动力矩向量。至此，在关节空间里，通过给定期望的角位移qd，角速度˙和角加速度，即可求解出机械臂各关节所需的驱动力矩τ，逆动力学问题得解。

以上文所得的所需驱动力矩τ作为已知量之一，加之以当前各关节角位移q与角速度˙作为剩余已知量，即可求解该机械臂的正运动学问题。即令式（11）中的＝［00－9.81］，则可得：

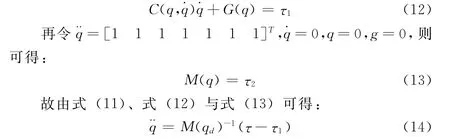
这是一种基于逆动力学解的正运动学求解算法。在文献［10］中，ShuujiKajita等得出了9自由度以下的机械臂采用这种算法可使正运动学问题的求解计算量更小。因此，本文也采用这种算法求解该机械臂的正动力学问题，并以此作为构建机械臂动力学仿真的基础，应用Robotics Toolbox for Matlab进行该机械臂的动力学建模与求解。

2 模糊自适应参数整定PID控制器设计

在工业现场，传统PID控制方法因其简单易操作性已得到了较为广泛的应用。传统PID在面对这些非线性时变的多自由度多刚体串联式开链系统时，其控制效果差强人意，难以达到系统精度要求。而模糊控制策略为改善传统PID在本文研究对象特定应用场景下的控制弱势提供了可参考的方案——模糊参数自整定PID控制策略［11 12］。

在机械臂实际运动的过程中，机械臂末端执行器的轨迹会受到自身各杆件转动惯量与重力的影响。由式（11）可知，只有当各关节驱动力矩τ可以较好模拟等式左边在输入为期望角位移qd，角速度和角加速度¨的期望输出力矩τd时，方可达到较好的控制效果。因此，在构造针对冗余度涂胶机器人的控制律u时，应该考虑添加重力补偿量g（q）。而除了重力补偿以外，摩擦力对机械臂控制精度也存在较大的影响。而一般地，在对机械臂驱动部件，如电机的内部具体参数不甚了解的情况下，较难对其摩擦力项进行准确建模。由于仅对机械臂进行动力学数值仿真，暂且忽略摩擦力对机械臂控制精度的影响。

2.1 控制的稳定性

由于对机械臂的控制最终反映到机械臂的工具坐标系即是对机械臂操作空间的控制。因此，在机械臂操作空间的模糊自适应PID控制策略中，设末端执行器的给定期望姿态常向量pd＝［xd，yd，zd，φd，ϑd，φd］T，实际姿态向量为pe，＝pd－p e＝［Δx，Δy，Δz，Δφ，Δϑ，Δφ］T作为本控制策略的控制量，控制目标是使得~p逐渐趋于零。现选择如下正定二次型的李雅普诺夫方程为：

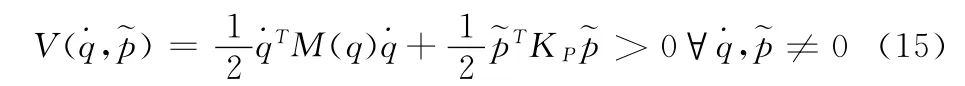
结合式（11）以及˙M（q）－2C（q，˙q）是斜对称阵的性质可得：

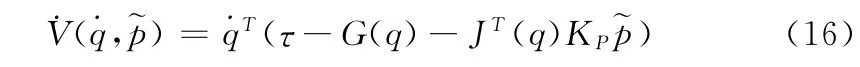
令上式中的τ用控制量u代替，可得：

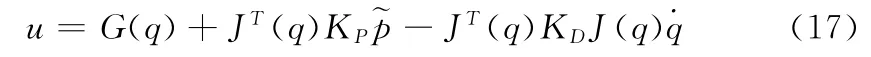
式中，KD是正定的微分增益矩阵。所以，式（16）可整理为：

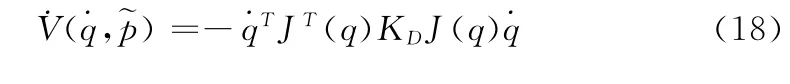
2.2 模糊自适应控制器的设计

本文的被控对象是冗余度涂胶机器人，由于对其进行位置控制是本文控制目标，所以控制系统主要针对机械臂末端执行器的空间姿态偏差量~p进行控制。

模糊自适应控制器正是利用控制系统被控制量与其对时间的微分量进行控制。在本系统中即是对空间姿态偏差量~p与空间姿态偏差量的变化率进行控制，通过对预先设置的比例微分增益值进行更新，得到比例微分增益的更新规律K′P＝ KP＋ΔKP和K′D＝KD＋ΔKD。模糊自适应控制器会根据当前的空间姿态偏差量及其变化率对系统增益进行实时更新，以期使得空间姿态偏差量及其变化率趋于零。根据此思路与前文分析所得的控制律u，设计出带重力补偿的模糊自适应PID控制系统示意图如图1所示。

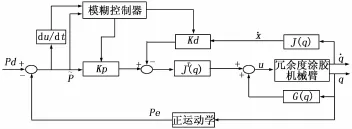
图1 重力补偿模糊PID控制示意框图

根据模糊控制理论的规范化离散论域设置规则，将误差论域设置为6个区域，即需要设置7个隶属度函数，并使其分别对应模糊化规则｛NB，NM，NS，0，PS，PM，PB｝，并完成模糊隶属度函数设置。对应ΔKP与ΔKD的模糊规则如表1与表2所示。

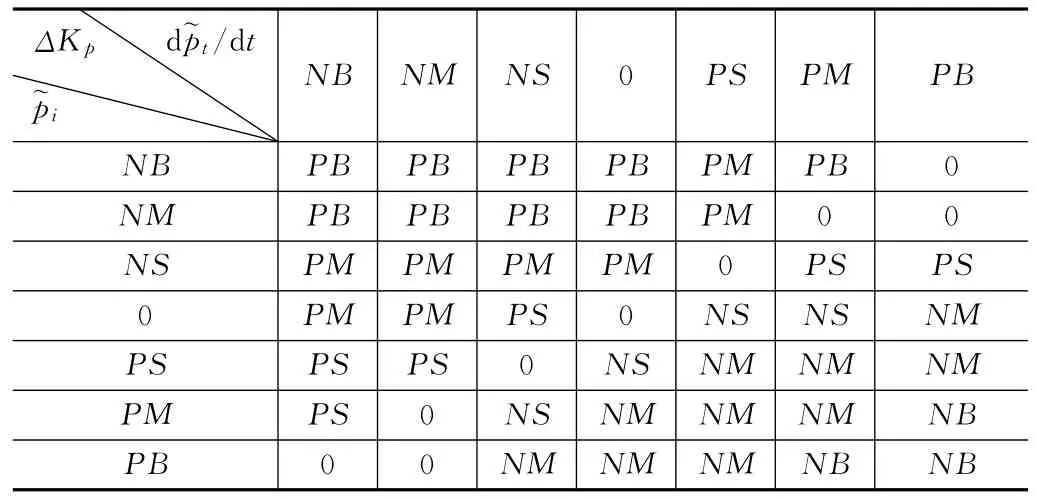
表1 ΔKp模糊规则表

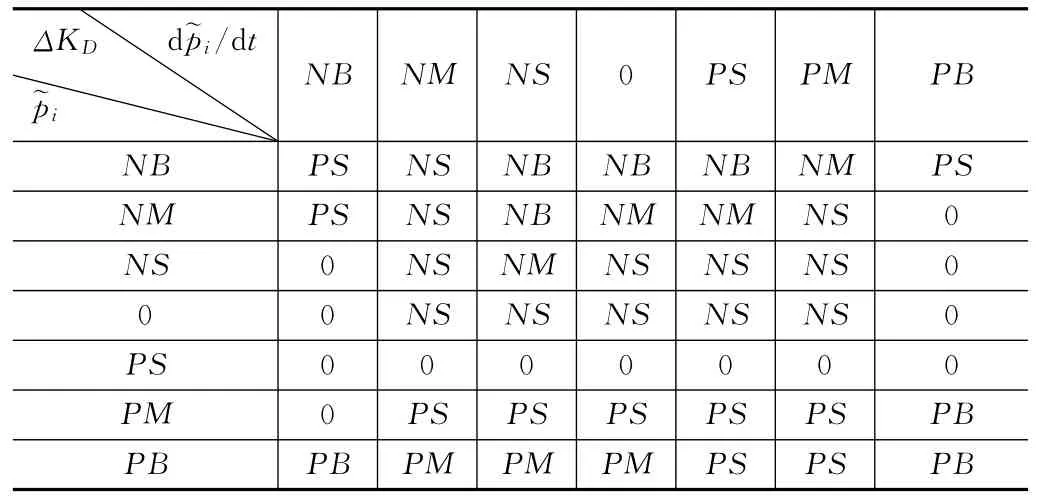
表2 ΔKD模糊规则表

图2是针对被控制量~p中的参数变化量Δx而设计的模糊控制器，该控制器分别以Δx与为输入量，并以针对Δx进行模糊控制的ΔKPx与ΔKDx为输出。其中，标号1表示本模糊控制器选择重心法为解模糊方式，标号2表示输入的范围，该范围即使用传统PID控制方法进行Matlab／Simulink仿真时Δx的变化范围。

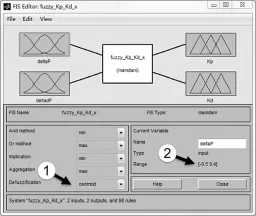
图2 参数变化量Δx模糊控制器

隶属度函数的设置，如图4所示。其中，图3（a）是对输入Δx隶属度函数的设置；图3（b）是对输出ΔKPx隶属度函数的设置，输出的范围根据传统PID控制方法进行Matlab／Simulink仿真时ΔKPx的变化范围进行估计。

图3 模糊控制器输入输出隶属度函数设置

使用上述方式设置针对Δy，Δz，Δφ，Δϑ，Δφ等参数变化量的模糊控制器可以得到如图4所示的模糊控制结构图。其中，标号1，2，3，4，5，6分别表示针对被控制量~p中的6个参数Δx，Δy，Δz，Δφ，Δϑ，Δφ分别设计的模糊控制器，7，8分别表示模糊控制器的输入向量与输出向量ΔKP，ΔKD，在Matlab／Simulink中使用subsystem（子系统）模块对该模糊控制器网络进行封装即得到本控制系统的模糊自适应控制器子系统。

图4 Matlab／Simulink模糊控制器内部结构图

3 冗余度涂胶机器人动力学仿真

根据前文的动力学分析与模糊PID控制器设计方案，利用Matlab／Simulink对冗余度涂胶机器人进行动力学控制仿真，通过与传统带重力补偿的PID控制仿真实验结果对比，

验证模糊自适应PID控制器的控制效果。

3.1 冗余度涂胶机器人的传统重力补偿PID控制动力学仿真

首先，根据前文在运动学分析中建立的冗余度涂胶机器人关节坐标系，并计算各杆件的动力学参数，建立该机械臂带重力补偿PID控制器如图5所示。图中标号1，2，3分别表示比例增益，微分增益与重力补偿模块。

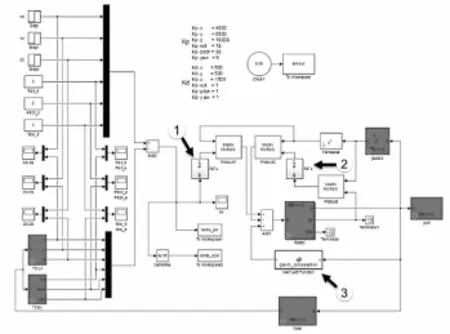
图5 冗余度涂胶机器人传统PID控制器（带重力补偿）

对系统进行仿真，设置系统仿真固定步长为0.01 s，对系统期望输入为机械臂末端工具在基坐标系下的空间姿态向量，其结构为［xd，yd，zd，φd，ϑd，φd］T，其中xd，yd，zd表示工具末端在基坐标系下的坐标，而φd，ϑd，φd分别表示工具坐标系绕基坐标系x，y，z轴的转角，对工具坐标xd，yd，zd与实际输出工具坐标xe，ye，ze进行两两对应观测。其中，仿真输入设置为阶跃信号；输入参数φd，ϑd，φd则均设置为常量0。参数设置完毕以后，对机械臂模型进行动力学仿真。通过调节PID参数，可以得出与被控量~p＝［Δx，Δy，Δz，Δφ，Δϑ，Δφ］T相对应的比例增益Kp与微分增益KD；仿真结果如图6所示。

由仿真结果可以看出系统输出能够较好地跟踪输入的信号，基本能在［1 s，2 s］的区间内达到稳定状态，消除震荡，基本消除稳态误差。

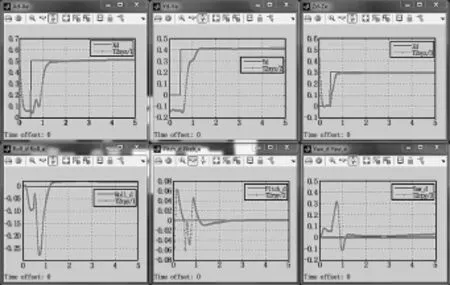
图6 冗余度涂胶机器人PID控制（带重力补偿）仿真输出图

3.2 冗余度涂胶机器人的重力补偿模糊自适应PID控制动力学仿真

利用上述仿真中对空间姿态变化量中各参数变化量Δx，Δy，Δz，Δφ，Δϑ，Δφ变化范围（误差范围）来确定模糊控制器隶属度函数误差论域阈值的设定，以此作为模糊控制器构建的参数依据，所构建的重力补偿模糊PID控制系统如图7所示。其中，标号1，2分别表示根据比例微分增益更新规律重新设计的比例、微分控制模块；3，4分别表示模糊控制器与重力补偿模块。

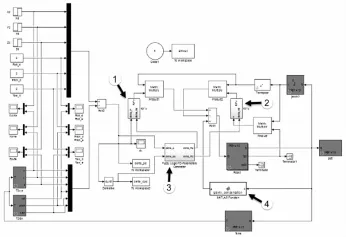
图7 冗余度涂胶机器人模糊自适应PID控制器（带重力补偿）

在相同仿真条件，相同输入的情况下，进行冗余度涂胶机器人在重力补偿的模糊自适应PID控制下的动力学仿真，仿真结果如图8所示。与图6对比，模糊PID控制下的机械臂的阶跃响应上升沿更陡，对输入的跟踪效果比传统的PID控制响应时间更短，而且稳态误差消除比传统PID控制彻底，显示出了重力补偿模糊自适应PID控制比传统PID控制更适用于本文研究的冗余度涂胶机器人。

图8 冗余度涂胶机器人模糊PID控制（带重力补偿）仿真结果图

4 结论

本文以具有7自由度工业涂胶机器人为研究对象，运用牛顿－欧拉分析法对冗余自由度涂胶机器人进行了动力学分析与建模。研究了适用于冗余度涂胶机器人的模糊参数自整定PID控制策略，建立了控制模型，并在Matlab／Simulink中运用Robotics Toolbox for Matlab工具箱对该机械臂进行了动力学建模与仿真。仿真实验以均有重力补偿的传统PID控制与模糊自适应PID控制为对比实验，实验结果表明模糊自适应PID控制方法比传统PID控制方法更适用于冗余度涂胶机器人，提高了系统精度，获得了更佳的鲁棒性，并达到更好的控制效果。

［1］咎 鹏，颜国正，于莲芝.基于自适应模糊PID控制的气动微型机器人系统［J］.仪器仪表学报，2007，9：1543-1547.

［2］Joo E M，Yang G.Robust adaptive control of robot manipulators using generalized fuzzy neural networks［J］.IEEE Transactions on Industrial Electronics，2003，50（6）：620-628.

［3］李 楠，李文鑫.改进的关节机器人神经网络PID控制器［J］.控制工程，2013，20（6）：1052-1054.

［4］刘国荣，张扬名.移动机器人轨迹跟踪的模糊PID－P型迭代学习控制［J］.电子学报，2013，41（8）：1536-1541.

［5］丁度坤，谢存禧.高速运动机器人关节神经网络PID自适应控制研究［J］.制造业自动化，2013，35（21）：18-20.

［6］任国华.移动机器人轨迹跟踪与运动控制［J］.机械设计与制造，2014，（3）：100-102.

［7］胡克满.基于改进型PID控制算法在小型仓储物流智能机器人中的应用研究［J］.物流技术，2012，（4）：24-27.

［8］Khatib O.Dynamics control of manipulator in operational space ［A］.Sixth IFTOMM Congress on Theory of Machines and Mechanisms［C］.New Delhi，1983：15-20.

［9］Khatib O.The operational space formulation in robot manipulator Control［A］.15th ISIR［C］.Tokyo，1985：11-13.

［10］Kajita S，Hirukawa H，Yokoi K，等.仿人机器人［M］.北京：清华大学出版社，2007.

［11］孙战磊，徐 开，王 栋，等.自适应模糊PID前馈补偿在机载挂飞摆扫转台控制中的应用［J］.计算机测量与控制，2015，23 （12）：4071-4074，4083.

［12］高庆吉，于婷婷，牛国臣，等.基于BP神经网络的多升降台同步控制研究［J］.计算机测量与控制，2015，23（07）：2340 -2343.

Study of Redundant Industrial Robot Control Based on Fuzzy Self－adaptation PID Control Algorithm

Ge Zhuo，Luo Qingsheng，Liang Guanhao

（School of Mechatronical Engineering，Beijing Institute of Technology，Beijing 100081，China）

In order to improve work efficiency and space utilization of gelatinizing process in automobile production line，a new type of redundant industrial robot with seven degrees of freedom was presented and a new type of control method was proposed.As it is known，the traditional PID control method had poor control effect dealing with nonlinear time－varying rigid－body series open chain system with multiple degrees of freedom.Based on the traditional PID control and fuzzy adaptive control algorithm，a parameter self－adaptation fuzzy PID control method with gravity compensation was proposed.Based on the Newton－Euler method，the dynamic model of this robot was established，and based on the dynamic model，the parameter self－adaptation fuzzy PID controller with gravity compensation was built.Several emulations used Matlab／Simulink software showed that the novel dynamic controller was a stable control system，and had better control effect comparing with PID controller.

redundant degree of freedom；industrial glue robot；dynamics；fuzzy self－adaptation

1671-4598（2016）08-0126-04

10.16526／j.cnki.11－4762／tp.2016.08.034

：TP2

：A

2016-03-16；

：2016-04-21。

北京市教育委员会科技计划面上项目（KM201310858004，KM201310858001）。

葛 卓（1988-），男，安徽马鞍山人，博士研究生，主要从事机器人控制系统设计、算法设计方向的研究。

罗庆生（1956-），男，教授，博士研究生导师，主要从事特种机器人技术、机电一体化技术方向的研究。