一类具有时滞的HIV-1型传染病模型的稳定性与Hopf分岔分析

郭少军, 寇春海, 申明圆

(东华大学 理学院, 上海 201620)

一类具有时滞的HIV-1型传染病模型的稳定性与Hopf分岔分析

郭少军, 寇春海, 申明圆

(东华大学 理学院, 上海 201620)

利用特征值理论分析了无病平衡点和地方病平衡点的局部渐近稳定性. 同时, 由于时滞τ的出现, Hopf分岔行为在系统中产生, 应用中心流形定理和规范形理论, 给出系统的分岔方向及分岔周期解稳定性计算公式. 最后, 通过数值模拟验证了理论分析结果.

传染病模型; 时滞; Hopf分岔; 稳定性

近年来, 在研究和分析HIV(艾滋病病毒)感染的动力学性态过程中, 数学模型的重要作用已被诸多研究所证明[1-3]. CD4+T细胞感染HIV模型的研究有了若干研究成果, 2014年, 文献[4]建立了一个五维系统并讨论了该系统的稳定性. 同时, 数学家对免疫时滞的病毒动力学模型也有了一些研究[5-9]. 由于从健康T细胞和病毒结合到能释放出病毒之间需要一段时间τ, 因此, 本文将在文献[4]研究的基础上考虑具有Holling II型感染率且带有时滞的HIV模型, 模型见式(1)所示. 式(1)中各参量的意义及取值见表1所示.

(1)

定义该模型的初始条件为

y1(θ)=φ1(θ), y2(θ)=φ2(θ),

y3(θ)=φ3(θ), y4(θ)=φ4(θ),

y5(θ)=φ5(θ)

(2)

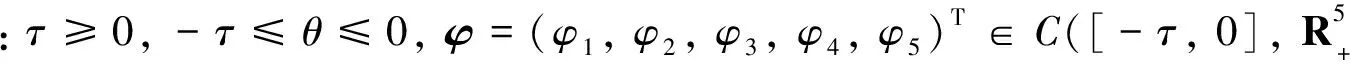
表1 各参数的含义和模拟中的取值[4]Table 1 The meaning and the simulation values of the parameters

在生物学的意义下, 假定φi(θ)≥0, θ∈[-τ, 0], i=1, 2, 3, 4, 5, 且式(1)中的所有系数均为正. 不难证明, 具有式(2)所示初始条件的式(1)模型的解总存在且为正.

1 平衡点的稳定性和Hopf分岔分析

(3)

1.1 无病平衡点E0的稳定性分析

定理1.1.1 当R0<1时, 对任意τ≥0, E0是局部渐近稳定的; 当R0>1时, E0是不稳定的．

证明: 式(1)模型在E0处的特征方程为

(4)

显然, ξ1, 2, 3=-d, -b, -h是方程式(4)的3个单重负根．考虑下面的超越方程

(5)

(1) 当τ=0时, 有

(6)

又

因此, 当τ=0时, 方程式(6)有两个负根, 即E0局部渐近稳定.

(2) 若τ>0时, 式(5)为超越方程, 设ξ=±iω为式(5)的纯虚根, ω>0, 将ξ代入式(5)得

(7)

分离实部和虚部并消去τ, 且令ω2=x, 有

(8)

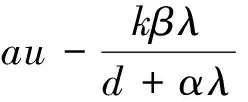
1.2 地方病平衡点E2的稳定性分析

式(1)模型在平衡点E2处的特征方程为

ξ5+p1ξ4+p2ξ3+p3ξ2+p4ξ+p5+

e-ξ τ(q1ξ3+q2ξ2+q3ξ+q4)=0

(9)

(1) 当τ=0时, 式(9)变形为

ξ5+p1ξ4+(p2+q1)ξ3+(p3+q2)ξ2+

(p4+q3)ξ+p5+q4=0

(10)

由Routh-Hurwiz判据可知, 方程(10)的根均有负实部的充要条件为

其中: a1=p1, a2=p2+q1, a3=p3+q2, a4=p4+q3, a5=p5+q4.

(2) 当τ>0时, 将ξ=iω(ω>0)代入式(9)中, 分离实部和虚部得

(11)

即

(12)

从式(12)中消去τ, 得

ω10+J1ω8+J2ω6+J3ω4+J4ω2+J5=0

(13)

m5+J1m4+J2m3+J3m2+J4m+J5=0

(14)

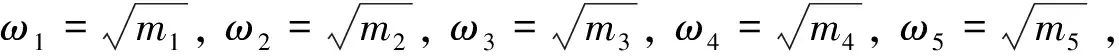
(15)

在方程式(9)中, 对τ进行微分可得

(16)

将ξ=iω0代入式(16), 有

(17)

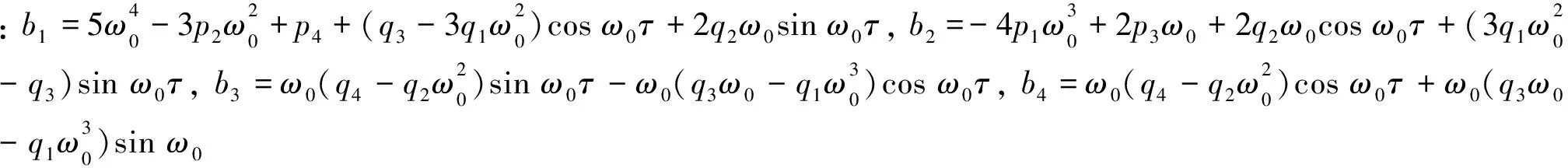
上面的分析可以得到下面定理1.2.1的结果.

定理1.2.1 当τ=τ0时, 式(1)模型在地方病平衡点E2处产生Hopf分岔.

2 Hopf分岔的方向及其稳定性

本节主要运用规范形原理和中心流形原理[10], 给出式(1)模型在分岔点τ=τ0处的准确公式, 这会决定Hopf分岔的方向、稳定性和周期解的周期性.

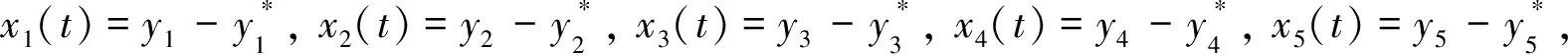
(18)

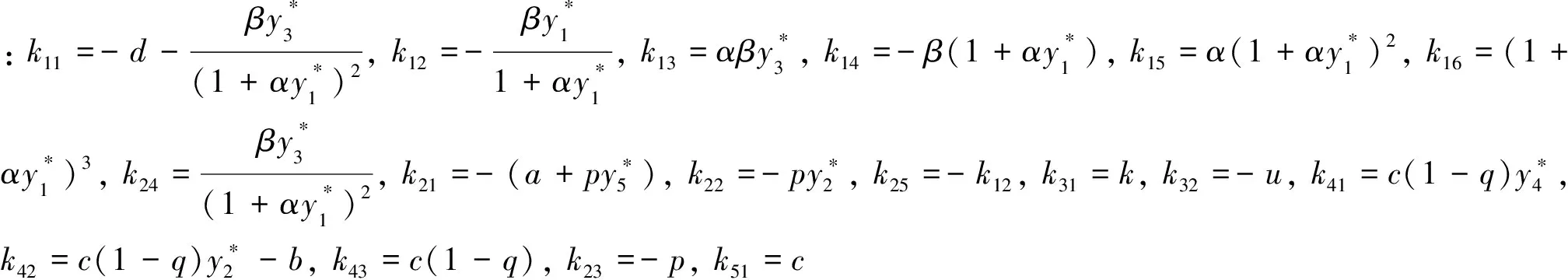
(19)

这里u(t)=(u1(t), u2(t), u3(t), u4(t), u5(t))T∈C([-τ, 0], R5), Lμ: C→R5定义为: 对φ∈C([-τ, 0], R5),

Lμφ=Q1φ(0)+Q2φ(-τ)

(20)

其中:

且

由Riesz表示引理[11]知, 存在一个5×5的有界变差矩阵函数η(θ, μ), θ∈[-τ, 0], 使得

(21)

选择

η(θ, μ)=Q1δ(θ)+Q2δ(θ+τ)

(22)

其中: δ(θ)是狄拉克函数. 因为φ∈C([-τ, 0], R5), 定义

(23)

且

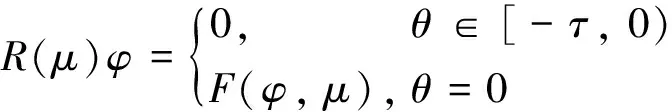
(24)

方程式(18)可以改写为

(25)

对于ψ∈C([-τ, 0], R5),A的伴随算子A*定义为

(26)

并定义双线性内积映射

(27)

(28)

由于A*的特征向量q*的表达式过长, 这里从略.

为了保证〈q*, q〉=1, 由式(27)可得

采用与文献[10]中同样的符号, 首先计算出中心流形C0在μ=0处的坐标.

定义

ut(θ)-2Re{Z(t)q(t)}

(29)

在中心流形C0上有

(30)

这里

(31)

(32)

(33)

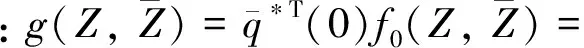
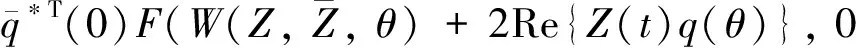
(34)

(35)

(36)

另外, 在C0上有

(37)

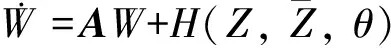
(38)

ut(θ)=(u1(t+θ), u2(t+θ), u3(t+θ),

u4(t+θ), u5(t+θ))

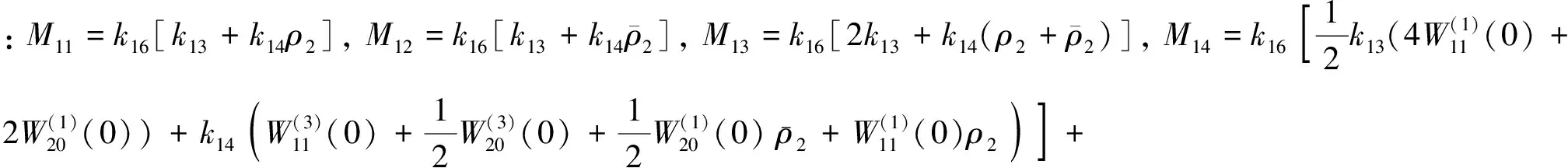
式(34)两边同乘以[k16+k15φ1(-τ)][k16+k15φ1(0)], 比较系数得

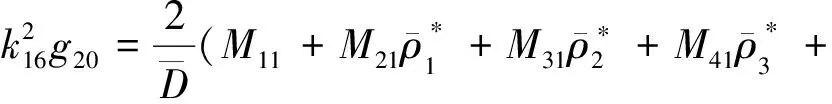
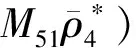
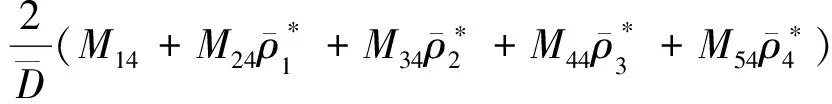
为了得到g21, 需要计算当θ∈[-τ, 0)时W20(θ)和W11(θ)的表达式. 从式(35)可知

将上式与式(36)比较系数得

(39)

由式(35)和(38)可得

(40)

解方程组(40)得

(41)

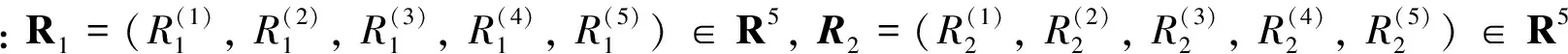
(42)

将方程式(36)两边同乘以[k16+k15φ1(-τ)][k16+k15φ1(0)], 与式(42)比较系数可得

2(M11, M21, M31, M41, M51)T

(M13, M23, M33, M43, M53)T

由A的定义和式(35)和(38), 得

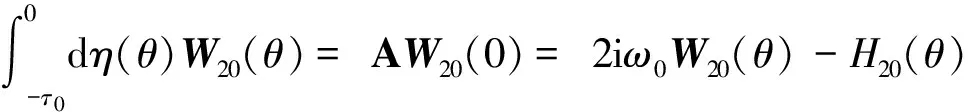
(43)

由特征值和特征向量的关系知

(44)

由式(41)～(44)得

M41, M51)T

从式(41)计算可得g21, 经过简单的计算可得:

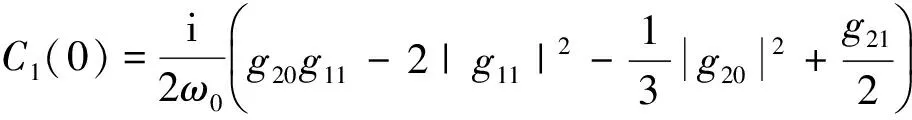
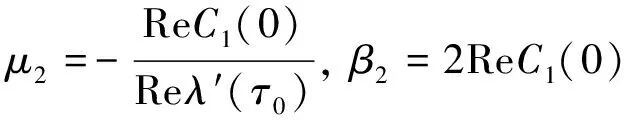
定理2.1 (1) Hopf分岔的方向可以由μ2确定, 如果μ2<0(μ2>0), 则Hopf分岔是亚临界(超临界)的; 并且当τ<τ0(τ>τ0)时, 分岔周期解存在.

(2) β2确定分岔周期解的稳定性. 若β2>0(β2<0), 那么分岔周期解是轨道不稳定(稳定)的.

(3) T2决定分岔周期解的周期性．若T2>0(T2<0), 那么分岔周期解的周期增大(减小).

3 数值模拟

本节通过数值仿真来证明本文理论分析结果的正确性. 式(1)模型中参数的选取参见表1: y1=0.5, y2=1.5, y3=0.1, y4=1.5, y5=1.5, d=0.1, p=1, β=0.007 5, a=1.5, u=8, c=0.1, k=25, q=0.1, b=0.2, h=0.1, α=0.031 25.

3.1 无病平衡点E0处的数值模拟

将各参数代入式(1)模型中, 据定理1.1.1的结论, 要求R0<1, 此时得到λ<6.400 0, 选取λ=λ1=4且τ=4进行数值模拟, 经计算可得E0=(40, 0, 0, 0, 0), 此时系统是渐近稳定的, 如图1所示.

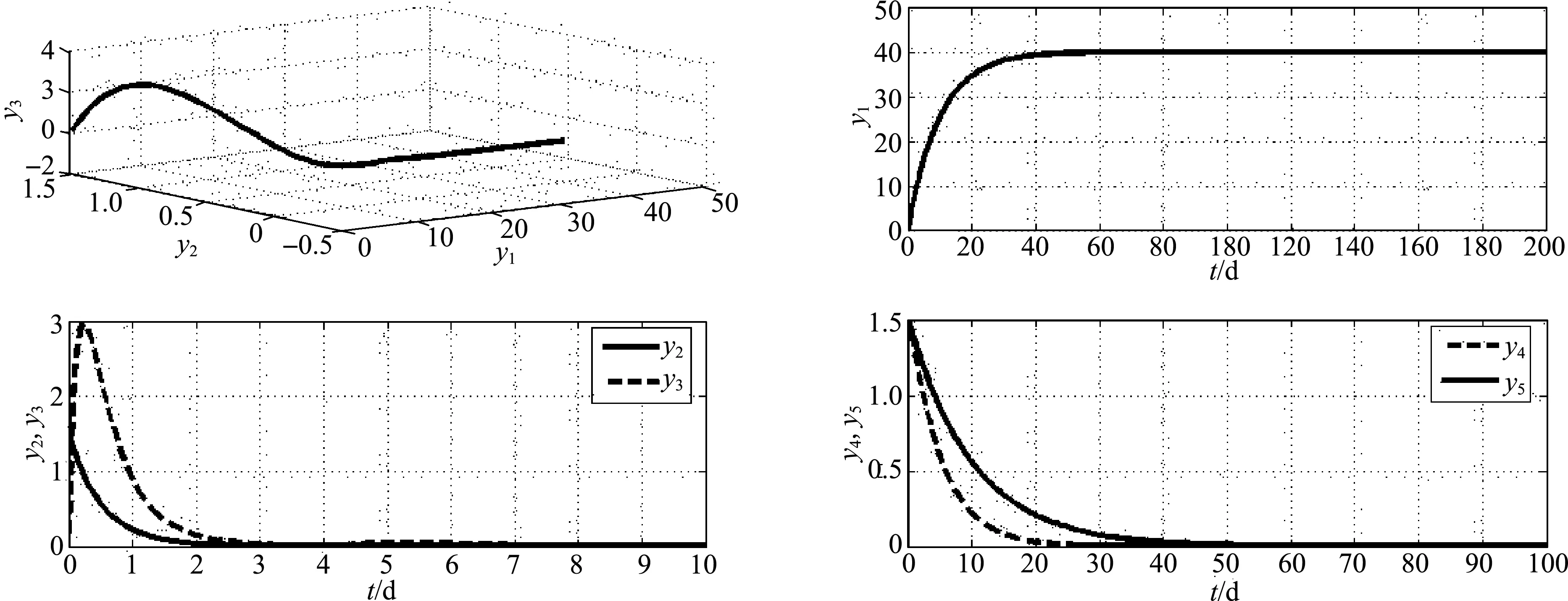
图1 τ=4, λ=4, 式(1)模型中各分量趋于平衡点的情况Fig.1 Each amount converge to their equilibrium with the parametic values τ=4, λ=4 in model (1)

3.2 地方病平衡点E2处的数值模拟

将各参数代入式(1)模型中, 据平衡点E2产生的条件R0>R1, 计算可得λ>7.511 1, 选取λ=λ2=10, 计算可得E2=(87.785 7, 2.222 2, 6.944 4, 0.223 4, 0.049 6). 此时由于时滞τ的影响, 系统会产生Hopf分岔现象. 通过Matlab计算可得: ω0≈0.145 5, τ0≈7.256 1, C1(0)≈0.379 2-6.485 7i, β2=0.758 4, μ2≈-5.712 8, T2≈3.657 1．由计算结果和定理2.1可知, 此分岔周期解是亚临界的, 如图2和3所示. 分岔周期解的周期随着τ的增大而增大, 如图4和5所示(图4为图2的局部放大图).

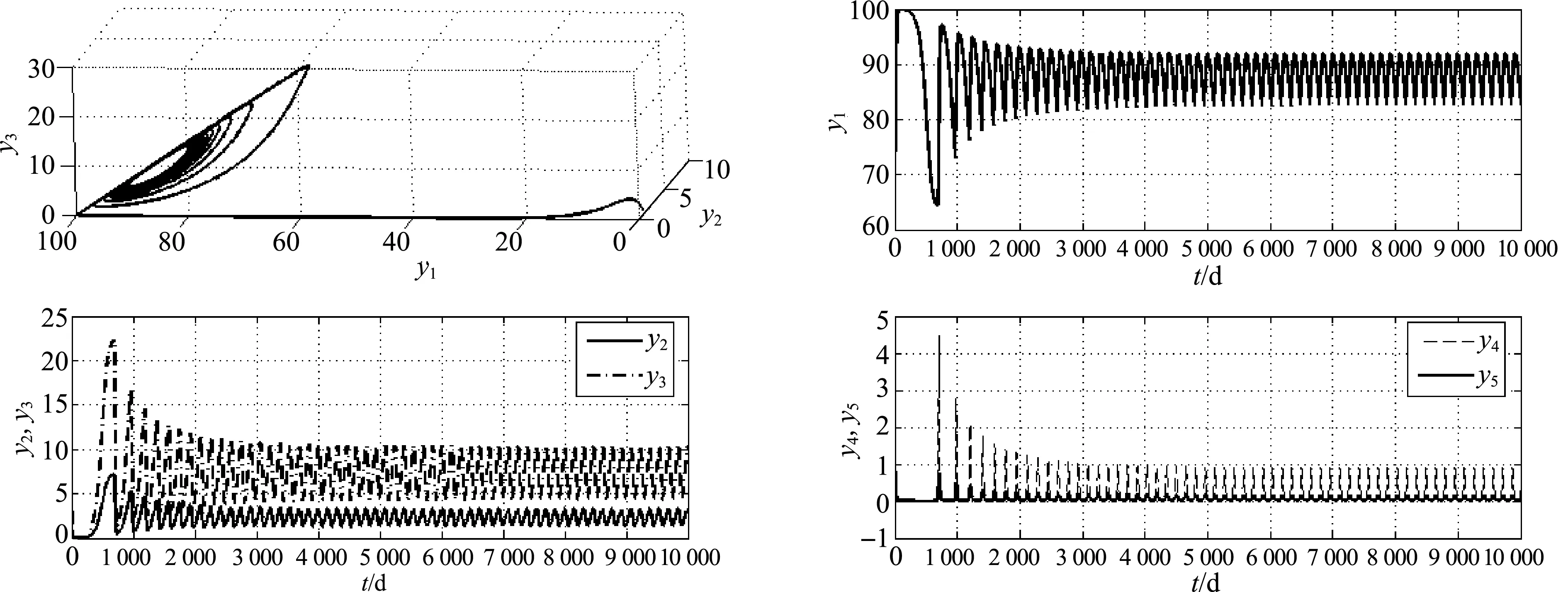
图2 τ=6, λ=10, 式(1)模型中各分量趋于平衡点的情况Fig.2 Each amount converge to their equilibrium with the parametic values τ=6, λ=10 in model (1)

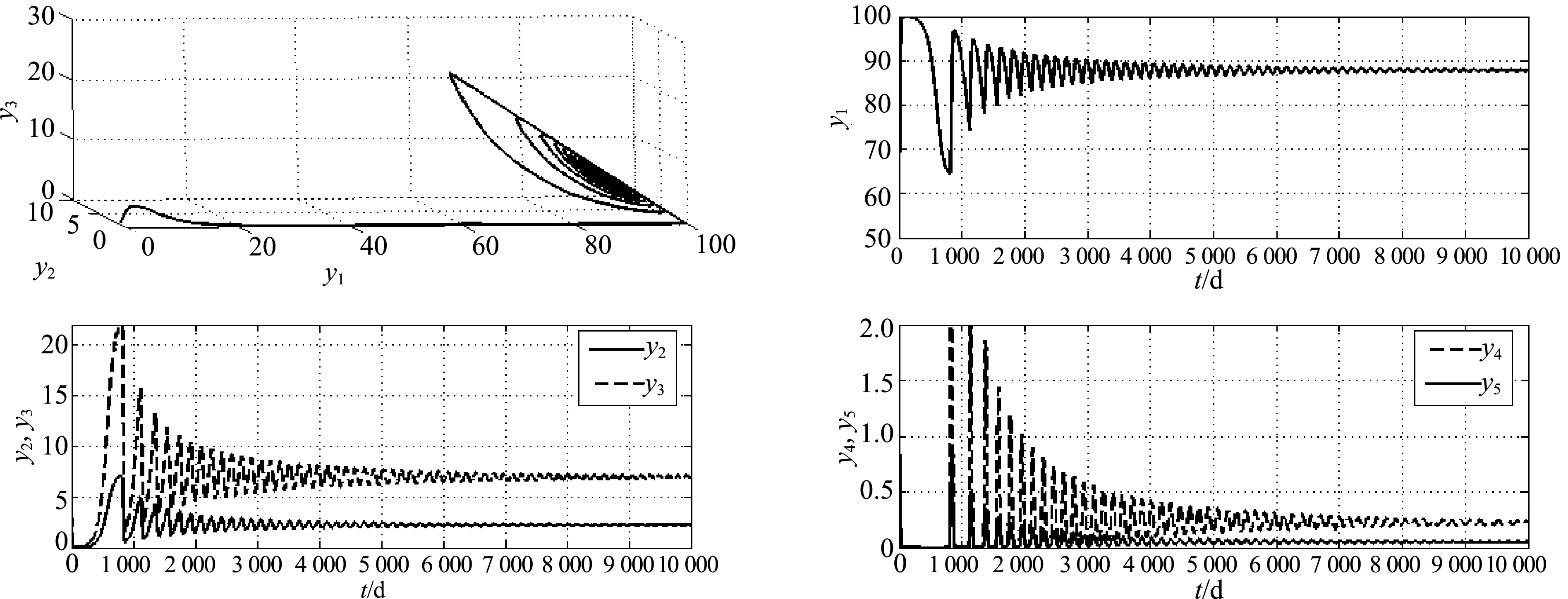
图3 τ=8, λ=10, 式(1)模型中各分量趋于平衡点的情况Fig.3 Each amount converge to their equilibrium with the parametic values τ=8, λ=10 in model (1)

图4 τ=6, λ=10, 式(1)模型中各分量趋于平衡点的情况Fig.4 Each amount converge to their equilibrium with the parametic values τ=6, λ=10 in model (1)

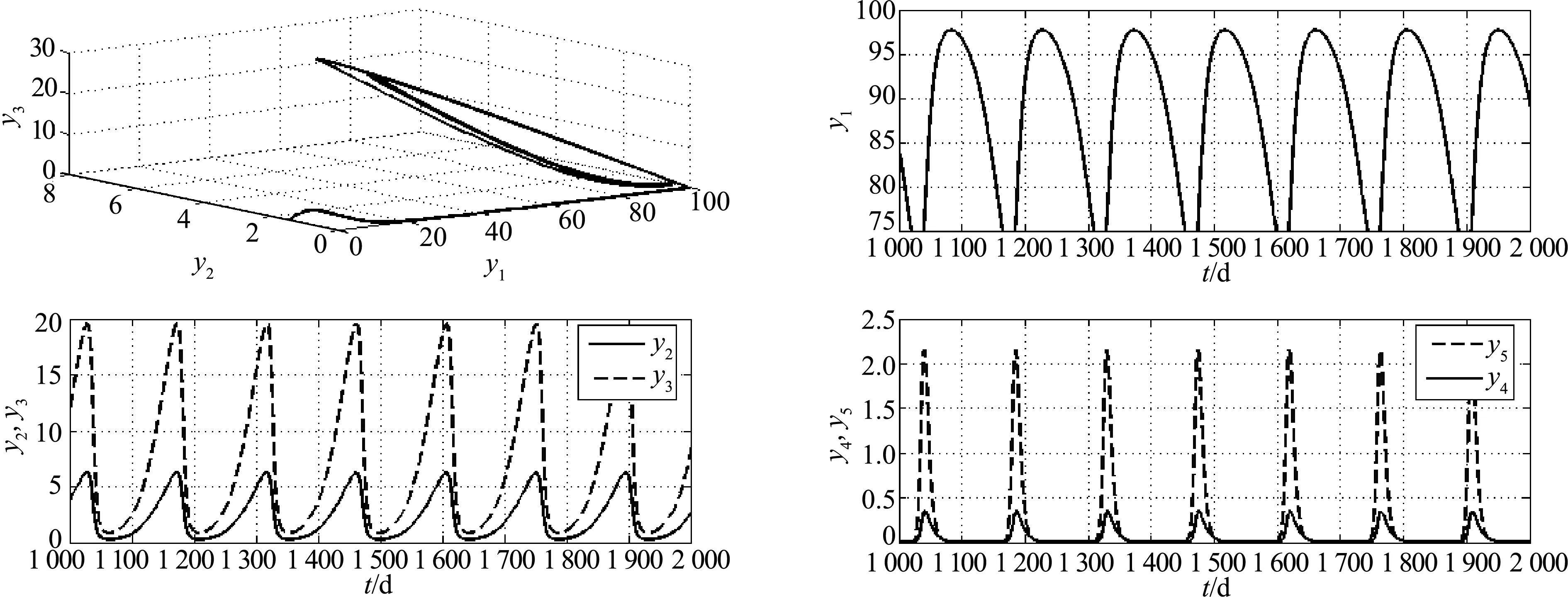
图5 τ=1, λ=10, 式(1)模型中各分量趋于平衡点的情况Fig.5 Each amount converge to their equilibrium with the parametic values τ=1, λ=10 in model (1)

3.3 不同抑制率α的数值模拟

仍取文献[4]中的各参数值, 其中λ=10, τ=8. 抑制率α分别取0.02, 0.03, 0.05时, 显示抑制率与已受HIV病毒感染的细胞浓度之间的关系, 如图4所示.

图6 λ=10, τ=8, 已受HIV病毒感染的细胞浓度在不同抑制率影响因素下的变化情况Fig.6 The concentration of infected cells by HIV under different inhibition rates with the parametic values λ=10, τ=8

4 结 语

本文研究了一类具有时滞且伴有非线性发生率的HIV-1型传染病模型， 分析了无病平衡点E0的局部渐近稳定性和不稳定性， 同时对地方病平衡点E2也进行了稳定性分析. 在R0>R1的条件下, 当τ=0时, 得到了地方病平衡点E2的局部渐近稳定的充分条件; 当τ>0且τ=τ0时, Hopf分岔现象出现在了地方病平衡点E2处, 即疾病会出现周期性爆发.本文运用了中心流形定理和规范形理论，对式(1)模型所出现的Hopf分岔方向和分岔周期解的稳定性以及分岔的周期进行了研究分析. 最终得出, 在式(1)模型中参数满足一定条件时, 式(1)模型出现了亚临界的Hopf分岔现象; 随着时滞量τ的增加, 分岔周期解的周期也在增加. 理论分析的正确性被进一步的数值模拟结果所证明. 为了验证抑制率α对疾病的影响效果, 通过一定的数值模拟得出, 适当地增大抑制率α, 会使得已受HIV感染的细胞浓度的最小值明显下降, 这对疾病的治疗时机的切入是有利的, 因此式(1)模型中引入抑制率α是必要的, 同时对生物学的研究具有重要意义. 但是, 在平衡点E1处进行平衡性分析过程中出现了异常复杂的数据, 这有待进一步研究论证.

[1] PERELSON A S, NEUMANN A U, MAEKOWITZ M. HIV-1 dynamics in divo: Virion clearance rate, infected cell life-span and viral generation time [J]. Science, 1996, 271(5255): 15821586.

[2] HO D D, NEUMANN A U, PERELSON A S. Rapid turnover of plasma virions and CD4+lymphocytes in HIV-1 infection[J]. Nature, 1995, 373: 123126.

[3] PERELSON A S, NELSON P W. Mathematical analysis of HIV-1 dynamicsin vivo[J]. Society for Industrial and Applied Mathematics, 1999, 41: 344.

[4] YU P, HUANG J N, JIANG J. Dynamics of an HIV-1 infection model with cell mediated immunity[J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19: 38273844.

[5] NOWAK M A, LLOYD A L, VADQUEZ G M, et al. Viral dynamics of primary viremia and antitroviral therapy in simian immunode ficiency virus infection[J]. Journal of Virology, 1997, 71(10): 75187525.

[6] SHI X, ZHOU X, SONG X. Dynamical behavior of a delay virus dynamics model with CTL immune response[J]. Nonlinear Analysis, 2010, 11: 17951809.

[7] XIE Q, HUANG D, ZHANG S. Analysis of a viral infection model with delayed immune response[J]. Applied Mathematical Modelling, 2010, 34: 23882395.

[8] WANG W D. Global behavior of an SEIRS epidemic model with time delays[J]. Applied Mathematics Letters, 2002, 15: 423428.

[9] KADDAR A. Stability analysis in a delayed SIR epidemic model with a saturated incidence rate[J]. Nonlinear Analysis Model Control, 2010, 15: 299306.

[10] HASSARD B D, KAZAARINOFF N D, WAN Y H. Theory and applications of Hopf bifurcation[M]. London: Cambridge University Press, 1981.

[11] 张恭庆, 郭懋正. 泛函分析[M]. 北京: 北京大学出版社, 1990: 3839.

Stability and Hopf Bifurcation Analysis of a Delay HIV-1 Epidemic Model

GUOShao-jun,KOUChun-hai,SHENMing-yuan

(College of Science, Donghua University, Shanghai 201620, China)

By analyzing the corresponding characteristic equation, the local stability of disease-free equilibrium and endemic equilibrium is discussed. The bifurcation property is obtained as the delay pass through a critical value. Applying the center manifold and normal form theory, some local bifurcation results are obtained and the formulas for determining the bifurcation direction and stability of the bifurcation periodic solution are derived. Finally, numerical simulations are presented to illustrate the theoretical analysis.

epidemic model; delay; Hopf bifurcation; stability

16710444 (2016)06-0906-10

2015-07-27

中央高校基本科研业务费专项基金资助项目(CUSF-DH-D-2015061)

郭少军(1988—),男, 山西保德人, 硕士研究生, 研究方向为常微分方程. E-mail：15021986290@163.com 寇春海(联系人),男,教授,E-mail：kouchunhai@dhu.edu.cn

O 175.6

A