梯度下降优化模糊系统的接触电阻预测方法

王刚， 谭盛武， 何子博， 林生军， 王之军， 常林晶

(1. 平高集团有限公司 国家电网高压开关设备绝缘材料实验室， 河南 平顶山 467001;2. 西安工业大学 材料与化工学院， 陕西 西安 710021)

梯度下降优化模糊系统的接触电阻预测方法

王刚1， 谭盛武1， 何子博2， 林生军1， 王之军1， 常林晶1

(1. 平高集团有限公司 国家电网高压开关设备绝缘材料实验室， 河南 平顶山 467001;2. 西安工业大学 材料与化工学院， 陕西 西安 710021)

根据接触电阻的特点，将结合模糊逻辑的预测方法引入电气领域，提出基于模糊系统的接触电阻预测新方法.根据接触电阻与各影响因素之间的关系及研究目的进行试验，得到足量试验数据，将所有试验数据分成两部分，训练数据和测试数据.通过训练数据运用梯度下降算法训练模糊系统，调整模糊系统参数，建立相应的接触电阻模型，利用训练数据建立接触电阻的回归分析模型.通过测试数据对两种模型进行测试，基于模糊系统的接触电阻模型的测试结果优于回归分析.预测与比较结果表明：若能得到足量训练数据，用梯度下降算法训练模糊系统建立的接触电阻模型精确可靠. 关键词： 接触电阻； 模糊系统； 梯度下降算法； 回归分析

电接触大量存在于电力电网、航空航天、交通运输等领域，如继电器的触头、电气设备的连接处等，训练误差为它的稳定性与可靠性对相关设备与系统的安全至关重要.一些军工、航空航天产品对电连接器的精度要求很高，微小的误差可能造成灾难性后果，因此,电接触的稳定性与可靠性一直是国内外研究的重点[1-8].接触电阻是反应电接触性能的重要参数，它便于测量.研究接触电阻的变化规律，建立高精度的接触电阻模型，对预测电接触失效具有重要意义[9-10].接触电阻是由收缩电阻和膜电阻组成.国内外学者做了大量工作，研究了基于理论的接触电阻模型.Holm[11]指出总接触电阻为所有接触点电阻的并联与因相互影响而形成的电阻的串联.Williamson[12]建立了接触电阻的二级收缩模型.Malucci[13]给出了接触电阻的三级收缩模型，该模型包含了收缩电阻和膜电阻.文献[14-15]综合考虑了收缩电阻和膜电阻，运用仿真的方法对接触电阻进行了计算.由于影响接触电阻的因素很多，且与接触电阻的关系较复杂，这使大部分接触电阻理论模型的精度和应用受到了一定限制.基于此，本文提出了基于模糊系统的接触电阻预测新方法.

1 模糊系统

近年来，应用广泛的M型模糊系统(具有模糊器和解模糊器的模糊系统)[16]吸取了纯模糊系统与TSK模糊系统的优点，克服了各自存在的缺点.所以,选用M型模糊系统，表示为

(1)

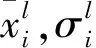
(2)

式(2)中：e为训练误差；N为训练数据数目；x0,y0为训练数据的输入和输出.

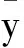
图1 模糊系统的应用过程Fig.1 Application process of fuzzy system

(3)

式(3)中:l=1,2,…,M;q=0,1,2,…;α为步长.

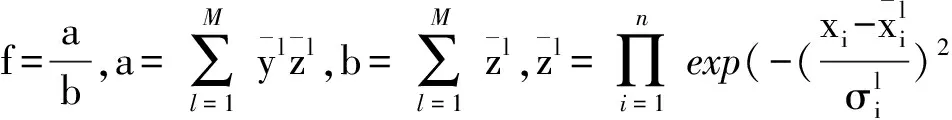
(4)

(5)

模糊系统的应用过程,如图1所示.

2 基于模糊系统的接触电阻模型

文中研究接触部分材料确定的情况下，接触电阻与接触压力、表面粗糙度的关系[17]，接触压力与螺栓的拧紧力矩成线性关系.所以,接触压力可以用连接螺栓的拧紧力矩表示，运用模糊系统进行建模，选取连接螺栓的拧紧力矩、接触处表面粗糙度作为模糊系统的输入，接触电阻作为模糊系统的输出.

试验在国家电网平高集团有限公司进行，试件为两块380 mm×800 mm的铝板，板厚20 mm，两铝板通过24个M16的螺栓连接，螺栓间的距离为60 mm.试验过程中,使用回路电阻测试仪进行接触电阻的测量.使用SATA 1/2”系列专业级可调式扭力扳手进行螺栓的预紧.

系统的输入参数：力矩T分别为40.0，76.0，85.5，95.0，104.5，114.0，123.5，133.0，142.5，152.0，161.5，171.0，180.5，190.0 N·m；表面粗糙度Ra分别为25.0，6.3，3.2 μm.

为了保证样本数据的准确和全面，采用全因子法设计试验，根据系统输入参数取值得试验共有42组样本数据.选出36组样本数据作为训练数据训练模糊系统，训练数据覆盖了样本空间的所有取值范围，同时达到了一定密度，剩下6组数据作为测试数据测试模糊系统，检测系统可靠性.试验重复3次，形成108组训练数据，18组测试数据.部分训练与测试数据,如表1,2所示.表1,2中：R为接触电阻.

表1 训练数据Tab．1 Trainingdata训练数据T/N·mRa/μmR/μΩ14025．09．82406．39．33403．29．0︙︙︙︙1081903．26．8表2 测试数据Tab．2 Testingdata测试数据T/N·mRa/μmR/μΩ185．56．37．82104．56．37．23123．53．27．2︙︙︙︙18180．53．26．4

2.1 模糊系统的初始化

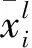
表3 模糊规则Tab.3 Fuzzy rules

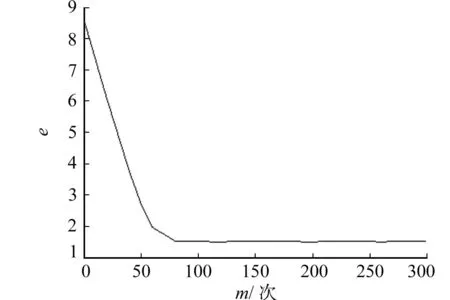
图2 模糊系统的训练Fig.2 Training of fuzzy system

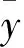
由表3可知：模糊规则1表示如果拧紧力矩T非常小(A1)，表面粗糙度Ra小(B3)，则接触电阻R为C11，其他模糊规则的含义类似.

2.2 模糊系统的训练

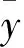
3 基于回归分析的接触电阻模型

工程上常用回归分析对试验数据进行处理，选择回归函数，通过最小二乘法对试验数据进行拟合.根据试验测得的接触电阻特点，回归函数取为全因子多项式.通过训练数据得到基于回归分析的接触电阻模型为

Δt=-4.149 8×10-5T2-1.222 2×10-4TRa-0.003 7Ra2-0.008 5T+0.141 4Ra+9.389 7.

拟合优度R2=0.9，拟合效果较理想.

4 模型测试

图3 各测试点的误差绝对值Fig.3 Absolute value of error of every point

采用测试数据对梯度下降算法训练模糊系统和回归分析模型进行测试，结果如图3所示.图3中：Re为测试误差绝对值.由图3可知：模糊系统模型的预测效果比回归分析模型好.

两种模型的测试误差绝对值最大值(Re,max)与平均值(Re,ave)，如图4,5所示.相对误差最大值(ηmax)与平均值(ηave),如图6,7所示.误差绝对值均方差(Ems，ae),如图8所示.相对误差均方差(Ems，re)，如图9所示.

由图4～9可知：梯度下降算法训练模糊系统所得接触电阻模型的预测效果较好，其测试误差绝对值的最大值为0.8 μΩ，平均值为0.59 μΩ，均方差为0.15 μΩ，相对误差的最大值为12.5%，平均值为8.48%，均方差为2.46%.与基于回归分析的接触电阻模型相比，误差绝对值平均值下降了0.39 μΩ，误差绝对值最大值下降了0.7 μΩ，误差绝对值均方差下降了 0.15 μΩ，相对误差平均值下降了5.33%，相对误差的最大值下降了8.3%，相对误差均方差下降1.49%.由此可知，由梯度下降算法训练模糊系统所得接触电阻模型优于回归分析.

图4 测试误差绝对值最大值 图5 误差绝对值平均值 图6 相对误差最大值Fig.4 Maximum of absolute value Fig.5 Mean value of absolute value Fig.6 Maximum of relative error

图7 相对误差平均值 图8 误差绝对值均方差 图9 相对误差均方差Fig.7 Mean value of relative error Fig.8 MSE of absolute value of error Fig.9 MSE of relative error

由于基于2次全因子多项式的回归分析无法体现螺栓预紧力矩、接触处表面粗糙度与接触电阻的关系，所以，回归分析的预测效果较差.由梯度下降算法训练模糊系统所得接触电阻模型能够较准确体现螺栓预紧力矩、接触处表面粗糙度与接触电阻的关系，所以，其预测效果优于回归分析.由梯度下降算法训练模糊系统所得接触电阻模型的各测试点预测值,如表4所示.回归分析的预测值,如表5所示.表4,5中：Rp为预测值；Re为误差绝对值；η为相对误差.

表4 模糊系统的预测结果Tab.4 Predictive result of fuzzy system

表5 回归分析预测结果Tab.5 Predictive result of regression analysis

由表4可知：当用第2组与第5组测试数据测试模糊系统时，误差绝对值达到最大0.8 μΩ，相对误差在第5组测试数据达到最大12.5%.由表5可知：当用测试数据测试回归分析模型时，误差绝对值和相对误差都在第2组测试数据达到最大，分别为1.5 μΩ和20.8%.

5 结束语

将基于模糊逻辑的系统建模方法引入电气领域，通过梯度下降算法训练模糊系统的方法对反映电接触性能的重要参数接触电阻进行建模，同时，建立了基于传统回归分析的接触电阻模型.对两种模型进行测试，检验其可靠性，并比较测试结果.预测与比较结果显示：由梯度下降算法训练模糊系统所得接触电阻模型的预测效果优于回归分析，该方法在接触电阻的预测方面具有优势.文中所提方法不仅能预测接触电阻，也为电气或其他领域内的复杂非线性问题提供了参考.

[1] REN Wanbin,WANG Peng,SONG Jian,etal.Effects of current load on wear and fretting corrosion of gold-plated electrical contacts[J].Tribology International,2014，70(70):75-82.

[2] TAMAI T,SAWADA S,HATTORI Y.Manifold decomposition processes of silicone vapor and electrical contact failure[C]∥Proceedings of the 26th International Conference on Electrical Contacts.Beijing:IEEE Press,2012:261-266.

[3] 王召斌,翟国富,黄晓毅.电磁继电器贮存期接触电阻增长的动力学模型[J].电工技术学报,2012,27(5):205-211.

[4] LU Ningyi,JIANG Changliu,CHEN Jun.Influence of coatings on contact resistance[C]∥Proceedings of the 26th International Conference on Electrical Contacts.Beijing:IEEE Press,2012:267-271.

[5] 王淑娟,余琼,翟国富.电磁继电器接触失效机理判别方法[J].电工技术学报,2010,25(8):38-44.

[6] WANG Shujuan,YU Qiong,REN Li，etal.Study on contact failure mechanisms of accelerated life test for relay reliability[J].IEICE Transactions on Electronics,2009,92(8):1034-1039.

[7] 杨文英,任万滨,翟国富,等.工频磁场对电磁继电器动态特性影响的三维有限元分析[J].电工技术学报,2011,26(1):51-56.

[8] 李玲玲,韩俊杰,王成山.基于灰色理论的继电器电接触可靠性预测[J].机械工程学报,2012,48(2):68-72.

[9] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.电气继电器 第26部分 量度继电器和保护装置的电磁兼容要求: GB/T 14598.20-2007[S].北京：中国标准出版社，2007：10-12.

[10] 孙立军.触点电接触失效预测理论的研究[D].天津:河北工业大学,2002:30-36.

[11] HOLM R.Electrical contacts[M].New York:Springer,1979:60-80.

[12] WILLIAMSON J B P.The microworld of the contact spot[C]∥27th Holm Conference on Electrical Contact.Chicago:IEEE Press,1981:1-10.

[13] MALUCCI R D.Multispot model of contacts based on surface features[C]∥Proc 36th IEEE Holm Conf Elect Contacts.Montreal:IEEE Press,1990:625-634.

[14] 李奎,张冠生,陆俭国.含膜触头静态接触下接触电阻有限元模型及其分析[J].电工技术学报,1998,13(1):27-31.

[15] SINGER M T.Electrical resistance of random rough contacting surfaces using fractal surface modeling the contact interface[J].IEEE Trans on CHMT,1991,14(1):73-82.

[16] 王立新.模糊系统与模糊控制教程[M].北京:清华大学出版社,2003:1-12.

[17] 胡星福,高华云,毛江虹.触头表面粗糙度对接触电阻影响的探讨[J].电工材料,2004(1):14-17.

(责任编辑： 黄晓楠 英文审校： 吴逢铁)

Method for Predicting Contact Resistance of Optimizing Fuzzy System by Gradient Descent Algorithm

WANG Gang1， TAN Shengwu1， HE Zibo2，LIN Shengjun1， WANG Zhijun1， CHANG Linjing1

(1. High Voltage Switchgear Insulating Materials Laboratory,State Grid (Pinggao Group Company Limited), Pingdingshan 467001, China;2. School of Materials and Chemical Engineering， Xi′an Technological University， Xi′an 710021, China)

Based on the characteristics of the contact resistance, the predicting method combined fuzzy logic is introduced to electric field, the new method for predicting the contact resistance based on fuzzy system is developed. According to relationship between contact resistance and influence factors, as well as the research target, the test is processed. The enough data is obtained and all data is divided into two parts， namely, training data and testing data. Fuzzy system is trained by gradient descent algorithm through training data, the systemic parameter is adjusted, the corresponding model of contact resistance is found. The regression analysis model of contact resistance is built by training data. The two models are tested through testing data, the prediction effect of the model based on fuzzy system is better than that of regression analysis. The prediction results show that if enough training data is obtained, the fuzzy system trained by gradient descent algorithm is reliable to predict the contact resistance. Keywords： contact resistance; fuzzy system; gradient descent algorithm; regression analysis

10.11830/ISSN.1000-5013.201701016

2016-03-28

王刚(1980-)，男，高级工程师，主要从事产品设计与仿真的研究.E-mail:wanggang2800@163.com.

国家高技术研究发展(863)计划项目(2014AA051802); 国家自然科学基金资助项目(51477120); 国家电网科技计划项目(SGNXJX00YJJS1400105)

TM 11

A

1000-5013(2017)01-0086-05