饱和砂土蠕变特性实验

王艳芳， 蔡燕燕， 蔡正银

(1. 南京大学 金陵学院， 江苏 南京 210093；2. 华侨大学 福建省隧道与城市地下空间工程技术研究中心， 福建 厦门 361021；3. 南京水利科学研究院 岩土工程研究所， 江苏 南京 210014)

饱和砂土蠕变特性实验

王艳芳1， 蔡燕燕2， 蔡正银3

(1. 南京大学 金陵学院， 江苏 南京 210093；2. 华侨大学 福建省隧道与城市地下空间工程技术研究中心， 福建 厦门 361021；3. 南京水利科学研究院 岩土工程研究所， 江苏 南京 210014)

为证实和进一步了解砂土蠕变规律，利用室内改装的应力控制式三轴仪研究饱和砂土排水蠕变特性.实验结果表明：砂土蠕变受围压和密实度的影响较大，低围压下，砂样更易发生剪胀；密实砂蠕变变形量明显比中密砂小，密实砂比中密砂更易剪胀；侧向减载条件比轴向加载更易剪胀；在应力水平不超过0.8的情况下，Mesri蠕变模型对砂土蠕变规律拟合效果较好. 关键词： 砂土； 排水蠕变特性； 剪胀； 密实度； Mesri蠕变

随着国民经济建设的发展，百年大计工程项目越来越多，对工程建设中地基和构筑物的长期稳定和变形问题提出了新的更高要求.不仅粘土的蠕变效应给工程项目的长期稳定和变形带来不利影响，无粘性土如坝体堆石料、砂土的蠕变[1-6]也对越来越多工程项目造成了不可忽视的影响.文献[7-13]通过室内实验和现场进行实测研究，发现长期开采地下水引起的地面沉降问题与砂土层压缩变形有密切关系，抽水或回灌引起水位升降导致砂层发生的变形并非弹性变形，而与时间存在一定关系，具有蠕变特性.对于软土，其蠕变多受含水量、土的结构、粘粒含量、有机质、应力历史、应力路径等主要因素影响[14-18]；对于软岩，其蠕变多受温度、湿度、应力路径等主要因素影响[19-22]；对于砂土，其蠕变多受土颗粒大小、形状、级配、密实度等因素影响[23-25].本文通过三轴试验研究饱和粉细砂的蠕变规律.

1 三轴蠕变试验

1.1 试验方案

王艳芳[26]通过对已建河北唐山京唐港10万t级遮帘桩板桩码头工程进行长期原位观测，发现泊位工程的前墙、遮帘桩、后锚定墙的侧向变形均存在时间效应，其原因为板桩结构两侧砂层蠕变位移.为此，文中取该区域一定数量粉细砂进行轴向加载和侧向减载条件下的三轴排水蠕变试验.砂样基本物理力学参数，如表1所示.表1中：γ为天然重度；Gs为土粒密度；ω为水的质量分数；Cq为粉细砂在固结快剪条件下的粘聚力；φq为内摩擦角；下标q表示的固结快剪条件.粉细砂的颗粒级配试验曲线，如图1所示.图1中；η为小于某直径的百分含量；d为试样直径.

图1 砂样颗分曲线Fig.1 Gradation curve of sand sample

土样γ/kN·m-3Gsω/%固结快剪指标Cq/kPaφq/(°)粉细砂19．72．6621．9031．1

试验仪器采用改装后的应力控制式三轴仪，尺寸为d=39.1 mm，H=80 mm.实验有如下5个步骤.

步骤1 制样.砂样直接在仪器基座上制备，称取相对密度(Dr)为60%，75%的粉细砂，并分3等份，分层击实.

步骤2 饱和.分初始饱和与反压饱和两步进行.初始饱和历时约1 h，测定孔隙应力系数(B)值大于0.8即可.接下来，反压饱和后B值须大于0.95才可进入下一步骤.

步骤3 等向固结.施加围压σ3使试样完成等向固结，砂样稳定固结时间约2 h，并记录等向固结时间内体变管读数，进行试样尺寸修正.

步骤4 不等向固结.以围压50 kPa为例，按k0=0.45，缓慢增加轴压至111 kPa，并静止.待试样完成k0固结，试样在24 h内轴向变形小于0.01 mm，视为完成不等向.固结此时体变管读数和轴向百分表读数，将其作为试样固结产生的初始体变、初始轴变值.

步骤5 排水蠕变实验.砂样蠕变试验加载方案,如表2所示.

表2 砂样蠕变试验加载方案Tab.2 Loading scheme of sand creep test

每级荷载施加后，一天内多次记录百分表读数及体变管读数.当连续1天土样轴向变形小于0.01 mm时，认为蠕变变形已稳定，可继续施加下一级加载，或结束试验[27].

1.2 试验结果分析

按照Boltzmann叠加原理，将各级围压作用下分级加载方式转化为分别加载方式的蠕变曲线，则砂样在轴向加载及侧向减载条件下，剪应变和体应变随时间的变化曲线，如图2～5所示.图2～5中：εs为剪应力；εv为体积应力；S为偏应力比，S=q/qf=(σ1-σ3)/(σ1-σ3)f.

由图2～5可知以下5点结论.

1) 实验未设定体积蠕变稳定标准，单从剪应变随时间变化曲线可看出：砂土的蠕变变形随着应力水平的增大而变大，没有出现等速蠕变和加速蠕变，为衰减蠕变.

2) 当没有剪胀时，体积变形较易稳定，一旦发生剪胀现象，体应变较难稳定.图2(f)表现为剪缩，图4(f)先剪缩后剪胀，其他组砂样体变均为剪胀.说明低围压条件下，砂样更易发生剪胀，且密实砂比中密砂更易剪胀.

3) 侧向减载条件下，砂样更易发生剪胀(图3，5).侧向减载条件下，所有砂样均为剪胀，说明应力路径会影响土体体积蠕变规律，且围压越低，剪胀效应越明显.

4) 密实度对砂样蠕变变形影响较大.密实砂蠕变量明显比中密砂小，即便是高偏应力水平下，在土样未破坏之前，密实砂的变形值仅为2%～4%(图4，5).进一步增大偏应力值，砂样只会剪坏，而不会像中密砂突变稳定后，还能进一步发生蠕变变形(图3(c)).

5) 砂土存在蠕变，砂土有良好渗透性，荷载作用很难引起超静孔压，几乎不存在次固结效应，其蠕变特性受围压和相对密实度的影响较大.因此，砂土蠕变机制细观上表现为在恒定荷载下，土颗粒位置的重新调整或部分破碎，宏观上表现为变形随时间而变化，即蠕变.

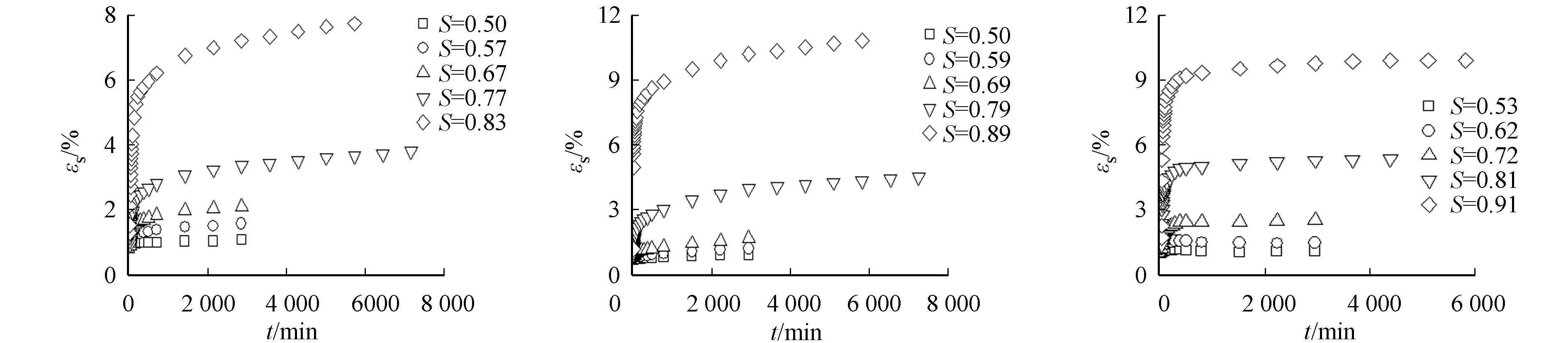
(a) σ3=50 kPa (b) σ3=100 kPa (c) σ3=250 kPa

(d) σ3=50 kPa (e) σ3=100 kPa (f) σ3=250 kPa图2 中密砂(Dr=60%)轴向加载蠕变曲线Fig.2 Creep curves under axial loading of middle dense sand (Dr=60%)

(a) σ3=50 kPa (b) σ3=100 kPa (c) σ3=250 kPa

(d) σ3=50 kPa (e) σ3=100 kPa (f) σ3=250 kPa图3 中密砂(Dr=60%)侧向减载蠕变曲线Fig.3 Creep curves under lateral unloading of middle dense sand (Dr=60%)

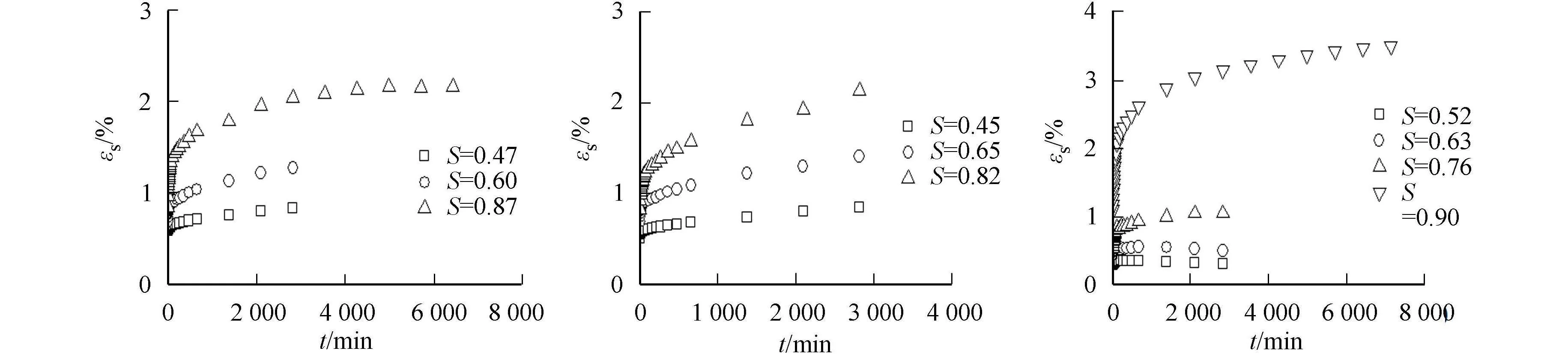
(a) σ3=50 kPa (b) σ3=100 kPa (c) σ3=250 kPa

(d) σ3=50 kPa (e) σ3=100 kPa (f) σ3=250 kPa图4 密实砂(Dr=75%)轴向加载蠕变曲线Fig.4 Creep curves under axial loading of dense sand (Dr=75%)

(a) σ3=50 kPa (b) σ3=100 kPa (c) σ3=250 kPa

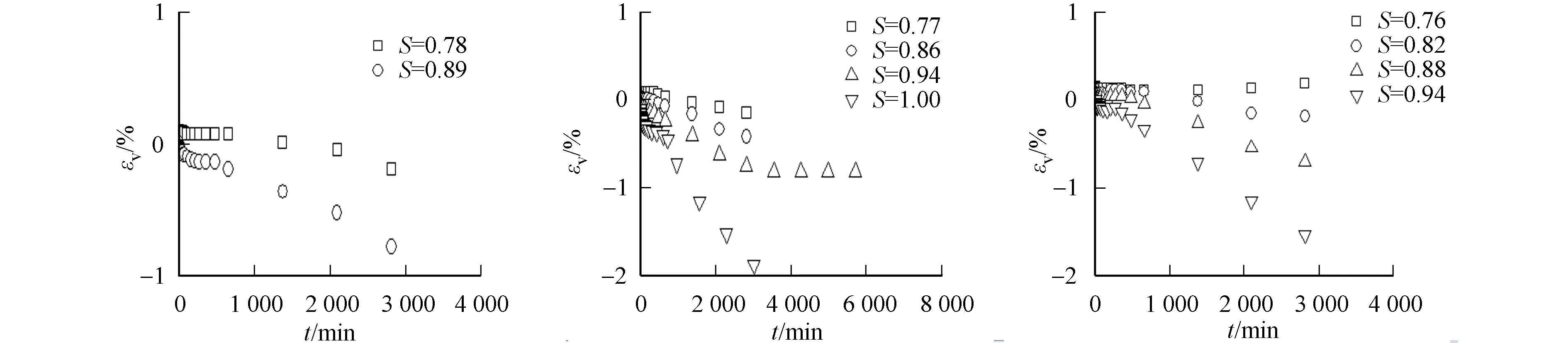
(d) σ3=50 kPa (e) σ3=100 kPa (f) σ3=250 kPa图5 密实砂(Dr=75%)侧向减载蠕变曲线Fig.5 Creep curves under lateral unloading of dense sand (Dr=75%)

2 Mesri蠕变模型

2.1 Mesri模型

基于蠕变试验结果，每级荷载下的总应变可分为瞬时应变及与时间有关的蠕应变两部分.蠕应变与应力、时间有关，一般可假设为

(1)

式(1)中：f1和f2分别为应力和时间的函数.

对于应力函数f1,Mesri借鉴Konder提出的应力-应变双曲线型方程[28-29]，即

(2)

式(2)中：S为偏应力比；Su为不排水剪切强度，Su=(1/2)(σ1-σ3)f.

对于排水试验，可以用Su=(1/2)(σ1-σ3)f代替.

对于时间函数，Mesri模型选用了幂次函数作为应变-时间关系，即

(3)

将式(2)，(3)相结合，得到Mesri模型，也即Mesri蠕变模型方程，其表达式为

(4)

由式(4)知，蠕变速率的公式为

(5)

2.2 模型参数的求取

根据lnεa-lnt关系，直线段位置选取参考时间t1=100min(因100min之前，lnεa-lnt直线关系不明显)，并取此时的应变为初始蠕应变.根据不同应力水平下的lnεa-lnt，拟合直线关系的斜率，求取平均值,即为λ值.

将式(2)作移项变换，有

(6)

表3 Mesri蠕变模型参数表Tab.3 Parameters of Mesri model

2.3 Mesri模型适应性

将表3中参数代入式(4)，拟合出砂土蠕变试验曲线如图6，7所示.图6,7中：εa为轴向应变;σ3=250 kPa.由图6,7可知：在应力水平不超过0.8的情况下，Mesri模型对砂土蠕变规律拟合效果较好，基本不受土样的密实程度、加卸载应力路径的的影响.

在高应力水平下，拟合效果不佳的原因有两个方面.一方面,在各级偏应力水平下，Mesri模型参数λ取lnεa～lnt拟合直线斜率的平均值，另一方面是经验模型本身精度所致.Mesri模型建议采用幂函数描述应变-时间关系曲线，幂函数拟合的曲线特点是缓慢地不断增长.曲线初期较陡，后期增加缓慢，导致其与试验曲线本身发展趋势的不完全吻合.而实际上λ是随着偏应力水平的变化而变化，相同围压、不同偏应力水平下的λ值相差也比较大.为此，建议可进一步修正Mesri蠕变法则，并将其与弹塑性模型相结合，建立起考虑砂土蠕变特性的弹粘塑性模型.考虑砂土蠕变规律与土体密实程度有关，尤其建议加入与密实度状态相关的参量，描述砂土蠕变规律.

(a) 轴向加载 (b) 侧向减载图6 中密(Dr=60%)砂样Mesri蠕变模型模拟结果Fig.6 Fitted curves of middle dense sandby Mesri creep model (Dr=60%)

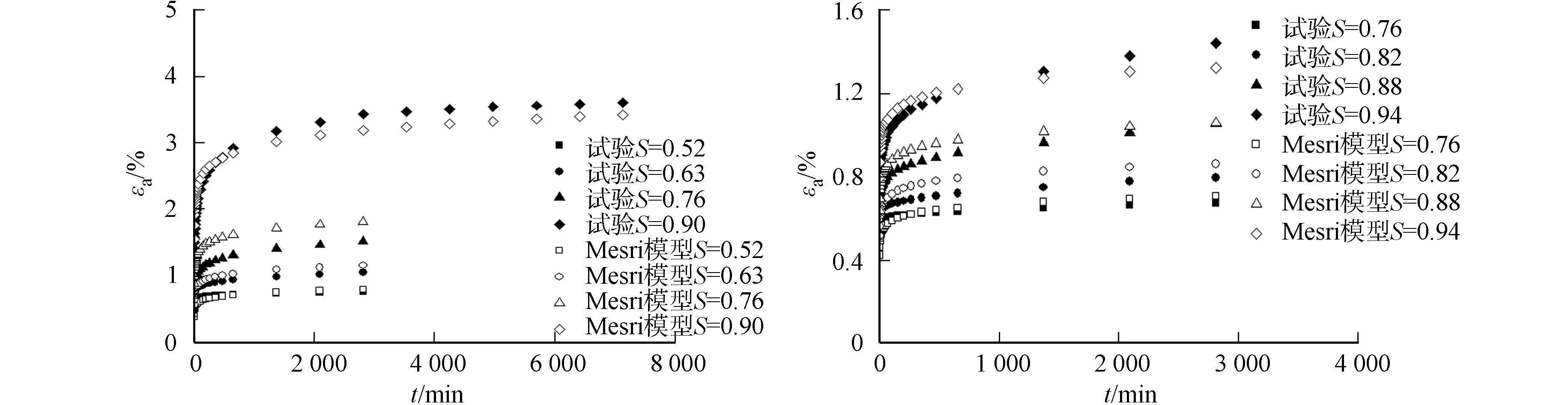
(a) 轴向加载 (b) 侧向减载图7 密实(Dr=75%)砂样Mesri模型模拟结果Fig.7 Fitted curves of dense sandby Mesri creep model (Dr=75%)

3 结论

1) 不论是轴向加载还是侧向减载蠕变，砂土变形规律基本一致，均证实了砂土存在蠕变.砂土蠕变特性受围压和相对密实度的影响较大，其蠕变变形随着应力水平的增大而变大.土样未破坏前，不管应力水平的高低，砂土的蠕变规律均为衰减型，没有出现等速蠕变和加速蠕变.

2) 试样体积应变明显小于剪应变，且低围压条件下，砂样易发生剪胀；密实砂比中密砂更易剪胀；侧向减载条件下，土体更易发生剪胀.当没有发生剪胀时，体积变形较容易稳定，一旦发生剪胀现象，体应变较难稳定.

3) 密实砂蠕变变形量明显比中密砂小.即便是高偏应力水平下，在土样未破坏之前，密实砂的变形值仅为2%～4%.进一步增大偏应力值，砂样只会剪坏，而不会像中密砂突变稳定后，还能进一步发生蠕变变形，故砂土蠕变特性必须考虑密实度对其蠕变规律的影响，且必须考虑体积剪胀效应的影响.

4) 依据Mesri经验蠕变模型，在应力水平不超过0.8的情况下，Mesri模型对砂土蠕变规律拟合效果较好，基本不受土样的密实程度、加卸载应力路径的的影响.对粉细砂或砂土而言，建议加入考虑与密实度状态相关的参量，以建立新的蠕变法则来描述其蠕变规律.

[1] BJERRUM L.Engineering geology of Norwegian normally consolidated marine clays as related to the settlement of buildings[J].Geotechnique,1967,17(2):81-118.

[2] 王者超,乔丽苹.土蠕变性质及其模型研究综述与讨论[J].岩土力学，2011,32(8):2251-2259.

[3] 杨超,汪稔,孟庆山.软土三轴剪切蠕变试验研究及模型分析[J].岩土力学,2012,33(增刊1):105-111.

[4] 卢萍珍,曾静,盛谦.软黏土蠕变试验及其经验模型研究[J].岩土力学,2008,29(4):1041-1045.

[5] 程展林,丁红顺.堆石料蠕变特性试验研究[J].岩土工程学报,2004,26(4):473-476.

[6] DIPRISCO C,IMPOSIMATO S.Time dependent mechanical behaviour of loose sands[J].Mechanics of Cohesive-frictional Materials,1996,1(1):45-73.

[7] SHI Xiaoqing,WU Jichun,YE Shujun,etal.Regional land subsidence simulation in Su-Xi-Chang area and Shanghai City[J].China Engineering Geology，2008，100(1/2):27-42.

[8] 孙晓涵.西安地面沉降与砂土蠕变关系初探[D].西安:长安大学，2011：35-40.

[9] 王非,缪林昌.抽水地面沉降中含水层长期变形特性研究[J].岩石力学与工程学报,2011,30(增刊1):3135-3140.

[10] WANG Fei,MIAO Linchang,ZHANG Yajun.A simplified method to predictcreep behavior of the Yangtze River sand[J].Bulletin of Engineering Geology and the Environment,2012,71(2):317-324.

[11] BURLAND J B,BURBRIDGE M C.Settlements of foundations on sand and gravel[J].Proceedings of the Institution of Civil Engineers,1985,78(6):1325-1381.

[12] 冷伍明,杨奇,聂如松，等.高速铁路桥梁桩基工后沉降组合预测研究[J].岩土力学,2011,32(11):3341-3348.

[13] 杨奇,冷伍明,聂如松，等.砂土蠕变特性试验研究[J].岩石力学与工程学报,2014,33(增刊2):4282-4286.

[14] 陈晓平,朱鸿鹄,张芳枝.软土变形时效特性的试验研究[J].岩石力学与工程学报,2005,24(12):2142-2148.

[15] 朱鸿鹄,陈晓平,程小俊,等.考虑排水条件的软土蠕变特性及模型研究[J].岩土力学，2006，27(5):694-698.

[16] 袁杰,房营光,谷任国,等.流变物质含量及其分布对软土蠕变特性影响的试验研究[J].岩石力学与工程学报,2014,33(增刊1):2924-2929.

[17] 谷任国,房营光.有机质和黏土矿物对软土流变性质影响的对比试验研究[J].华南理工大学学报(自然科学版),2008,36(10):31-36.

[18] 杨爱武,闫澍旺,杜东菊.结构性吹填软土蠕变模型研究[J].岩土力学，2012,33(11):3213-3219.

[19] 杨春和,白世伟,吴益民.应力水平及加载路径对盐岩时效的影响[J].岩石力学与工程学报,2000,19(3):270-275.

[20] 张向东,傅强.泥岩三轴蠕变实验研究[J].应用力学学报,2012,29(2):154-159.

[21] 高小平,杨春和,吴文,等.盐岩蠕变特性温度效应的实验研究[J].岩石力学与工程学报,2005,24(12):2054-2059.

[22] 谌文武,原鹏博,刘小伟.分级加载条件下红层软岩蠕变特性试验研究[J].岩石力学与工程学报,2009,28(增刊1):3075-3080.

[23] 胡桂衔,房营光,袁杰.砂性土的蠕变性质影响试验研究[J].工程勘察,2012(12):8-11.

[24] 张云，薛禹群，施小清，等.饱和砂性土非线性蠕变模型试验研究[J].岩土力学,2005,26(12):1869-1873.

[25] 张云,薛禹群,吴吉，等.上海砂土蠕变变形特征的试验研究[J].岩土力学,2009,30(5):1226-1231.

[26] 王艳芳.饱和土蠕变特性试验及计算模型研究[D].南京:南京水利科学研究院,2012:131-135.

[27] 王艳芳,蔡正银,周治刚,等.k0固结条件下淤泥土排水蠕变特性研究[J].岩土力学,2015,36(8):2243- 2248.

[28] 李军世,孙钧.上海淤泥质粘土的Mesri蠕变模型[J].土木工程学报,2001,34(6):74-79.

[29] MESRI G,REBERS-CORDERO E,SHIELDS D R,etal.Shear stress-strain-time behavior of clays[J].Geotechnique,1981,31(4):537-552.

[30] 赖小玲,叶为民,王世梅.滑坡滑带土非饱和蠕变特性试验研究[J].岩土工程学报,2012,34(2):286-292.

(责任编辑： 陈志贤 英文审校： 方德平)

Experimental Investigation of Creep Properties of Saturated Sand

WANG Yanfang1, CAI Yanyan2, CAI Zhengyin3

(1. Jinling College, Nanjing University, Nanjing 210093, China;2. Fujian Engineering Technology Research Center for Tunnel and Underground Space,Huaqiao University, Xiamen 361021, China;3. Geotechnical Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210014, China)

In order to verify and investigate further the sandy soil creep properties, the stress-controlled triaxial apparatuses are used to study the drainage creep of saturated sand. The result shows that the creep of saturated sand is significantly affected by confining pressure and dense degree. Under low confining pressure, the sample shear dilatancy occurs easily. The creep deformation of dense sand is significantly smaller than the deformation of middle dense sand, the dense sand shear dilatancy occurs more frequently by comparison with middle dense sand. When the stress level is less than 0.8, the Mesri creep model is fitted well for sandy soil creep. Keywords： sand; drained creep property; shear dilatancy; dense degree; Mesri creep

10.11830/ISSN.1000-5013.201701006

2016-05-28

王艳芳(1983-)，女，副教授，博士，主要从事岩土工程方面的研究.E-mail:wyf_02@163.com.

国家自然科学基金资助项目(51308234)

TU 447

A

1000-5013(2017)01-0031-07