矩阵变换器驱动的永磁同步电动机电流及速度控制技术

于海丽, 王军, 孙文磊

(1. 新疆农业职业技术学院 工程学院， 新疆 昌吉 831100；2. 南京工业大学 机械与动力工程学院， 江苏 南京 211800;3. 新疆大学 机械工程学院， 新疆 乌鲁木齐 830047)

矩阵变换器驱动的永磁同步电动机电流及速度控制技术

于海丽1, 王军2, 孙文磊3

(1. 新疆农业职业技术学院 工程学院， 新疆 昌吉 831100；2. 南京工业大学 机械与动力工程学院， 江苏 南京 211800;3. 新疆大学 机械工程学院， 新疆 乌鲁木齐 830047)

针对矩阵变换器驱动的永磁同步电动机电流和速度控制问题，提出一种有限集模型预测控制算法.不同于传统的矩阵变换器控制方法，该算法通过使用输入滤波器成本函数和电机速度成本函数，实现直接控制瞬态和稳态条件下的输入电流，形成高动态响应,从而避免在电压瞬变期间输入滤波器电流产生不必要的振动.此外，还提出一种新的输入滤波器观测器，可以减少传感器的数量，从而增加系统的可靠性并降低成本.通过仿真及实验,对提出算法的有效性进行验证，结果表明：该算法具有动态优势. 关键词： 有限集模型； 预测控制； 矩阵变换器； 永磁同步电动机; 成本函数

近年来,用以替代电源转换器传统控制策略的有限集模型预测控制(FCS-MPC)日益受到人们的关注[1-3].有限集模型预测控制通过控制系统模型，预测系统本身的下一状态.然后，通过最小成本函数选择最佳的控制动作，该策略可以同时直接控制多个状态变量.一些学者对其进行了研究[4-6],但这些调制策略的共同缺点是不能直接控制输入滤波器电流,从而造成共振系统的不稳定性.由于动态性能和功率密度较高，永磁同步电机广泛地应用于工业生产中.永磁同步电机(PMSM)和矩阵变换器(MC)组合形成一个四象限的驱动系统，质量和大小可以很低[7].驱动系统的典型控制策略是由级联线性控制器、高动态内部电流环和相对较慢的外部速度控制回路构成.通过标准的两级变换器控制，单独使用有限集模型预测控制，可控制永磁同步电机电流和速度[8-9]，但其算法复杂性和成本较高，实际操作困难.本文提出一种有限集模型预测控制算法，用矩阵变换器来控制永磁同步电机的电流和速度.

图1 矩阵变换器的示意图Fig.1 Schematic diagram of matrix converter

1 系统模型

有限集模型预测控制利用系统模型预测系统本身的下一状态.因此,模型的定义是成功实现控制策略的关键点.作为永磁同步电机的电机驱动器，矩阵变换器的示意图，如图1所示.Vi，Io分别为

(1)

式(1)中:Vi为矩阵变换器的输入电压；Io为矩阵变换器的输出电流.

图2 输入滤波器的示意图Fig.2 Schematic diagram of input filter

矩阵变换器通常需要一个输入滤波器来过滤电流，以避免切换期间造成电压峰值.文中的无源(LC)滤波器示意图，如图2所示.假设系统是平衡的，图2中只显示了一个阶段.同样,在以下方程中将省略识别阶段的下标.Rf为过滤器组件的寄生电阻,因为文中没有运用阻尼电阻.该输入阶段的模型为

(2)

根据文献[10]的方法，源电压Vs可以视为正弦，频率固定.因此，可以将其视为一个系统正弦扰动，利用观测器进行估算.由Vs预测Is和Vi未来的数值，并计算最佳控制值.

正弦扰动通用的状态空间为

(3)

式(3)中:ω为干扰脉冲.

合并式(2)，(3),可得

(4)

新的过滤模型公式变为

(5)

(6)

(7)

新的增广状态向量和控制输入变为

(8)

仅运用电流Is和电压Vi的测量值，可以为系统(5)构建一个观测器.系统(5)必须进行离散采样，公式为

(9)

(10)

式(10)中:T为采样时间；k和k+1等下标为系统采样时间点.此外，通过采用电流Is和电压Vi的非过滤值，有限集模型预测控制性能更佳.因此，运用降阶观测器估算线性电压,可降低控制算法的复杂性.

式(8)中定义的系统状态可拆分为

(11)

式(11)中:上标a和b用于区别两个子状态.

式(9)可以重新表述为

(12)

观测器可以表示为

(13)

(14)

上述观测器无需电源电压传感器,从而增加系统的可靠性，降低成本.此外,即使没有输入滤波电感，还可以使用有限集模型预测控制,例如,当变压器存在于线性端时.

因此，对于矩阵变换器驱动的永磁同步电机模型而言，其扰动观测器可以表示为

(15)

(16)

(17)

2 有限集模型预测控制算法

有限集模型预测控制算法步骤，如图3所示.在第k个采样阶段开始时，利用式(13),(15)将描述的2种观测器中的所有系统加以更新.

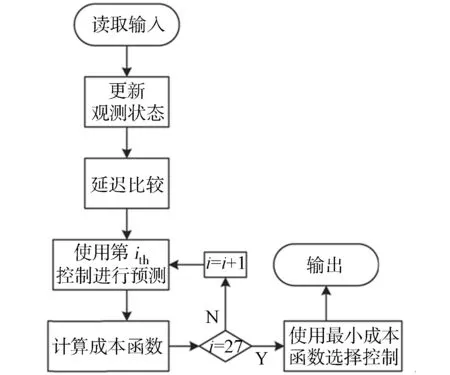
图3 有限集模型预测控制算法步骤Fig.3 Proposed finite set model predictive control algorithm

有限集模型预测控制需要的计算成本高、采样频率高，这表明可以运用新的控制动作，但仅限于在下一次采集时段开始时.这就造成采样时段的延迟，延长需要补偿.为了完成该任务，运用在第(k-1)个采样时段获得的最佳控制,计算在第(k+1)个采样时段的系统状态.这个操作对应于观测器的预测步骤(式(14)，(16)，(17)).

因此,只可以用计算得到的最优值计算一次.随后,在第(k+2)个采样周期中，为27个可能的矩阵变换器开关组态分别计算一次系统状态.然后，利用系统状态,计算成本函数.通过选择矩阵变换器的开关组态选择最优控制，可以产生最低的成本函数值和频率.

3 成本函数的选择

在实施提出算法的过程中，成本函数的选择至关重要.如果成本函数选择恰当的话，与传统的控制方案相比，它可以控制不同的状态变量.

3.1 输入滤波器成本函数

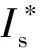
(18)

矩阵变换器输入端的功率表示为

(19)

将式(18)代入式(19)中，R(*)表示实数部分，S(*)表示虚数部分,有

(20)

假设使用单一功率因数，在变换器的输出端，功率可以表示为

(21)

式(21)中:Id值可以忽略,电机铁损也可忽略.

输入和输出矩阵变换器的功率可以与转换器的效率相关联.在电机运行模式下,其关系表示为

(22)

在更新模式中，式(22)变为

(23)

将式(20),(21)代入式(22)中，求出电流值Is.最后，计算参考电流源模块,即

(24)

(25)

在电力稳定的状态下，提出的电流参考更新方法是正确的.但是,电力变量存在瞬态变化,且通过实验验证,在瞬变期间，应用文中提出的方法并不影响大部分系统性能.

由式(24)可知，相对于在第k个采样时间点的输入滤波器而言，成本函数可以被定义为

(26)

式(26)中:下标α,β表示在α～β区域转变的数量.该成本函数确保输入电流为正弦，功率因数统一.与文献[9-10]中所使用的无功功率最小化的方法相比较，使用正弦参考值,可以避免由于输入滤波器造成的共振，使系统变得不稳定,即使在低阻尼存在的情况下,也不影响系统的动态性能.成本函数的使用稍微减少了电动机的性能.然而,在矩阵变换器输入端更需要稳定性.

3.2 永磁同步电动机成本函数

用于控制永磁同步电动机侧的主要变量是马达的速度.使用平方误差,在第k个采样时间点的速度成本函数定义为

(27)

(28)

(29)

其中：

(30)

(31)

(32)

(33)

(34)

4 实验结果

通过实际实验对控制算法进行测试.使用C6713型数字信号处理器(美国德克萨斯州仪器公司)，采样时间为20μs.应用SK60GM123IGBT模块实现矩阵控制器原型.永磁同步电动机主要参数如下：Rm为1Ω；Lm为3.2mH；np为10；φ为0.126Wb；J为0.126kg·m2；Ba为9.62×10-3N·s·m-1.输入滤波器的参数如下：Lt为0.4mH；Cf为4；Rt为1.感应滤波器具备Δ连接的电容器，文中没有使用阻尼电阻.使用卡尔曼滤波器的方法，调整输入过滤器观测器增益K，以便将观测器的极点设置在频率约为50Hz，阻尼因子为0.707.

测量和估算的相间电压源的比较，如图4所示.图4中：Va,b为电压；ΔV为误差.通过试验验证调整电动机端的观测器，处理系统机械共振.采用极点配置方法,设置增益以获得大约5Hz的带宽.

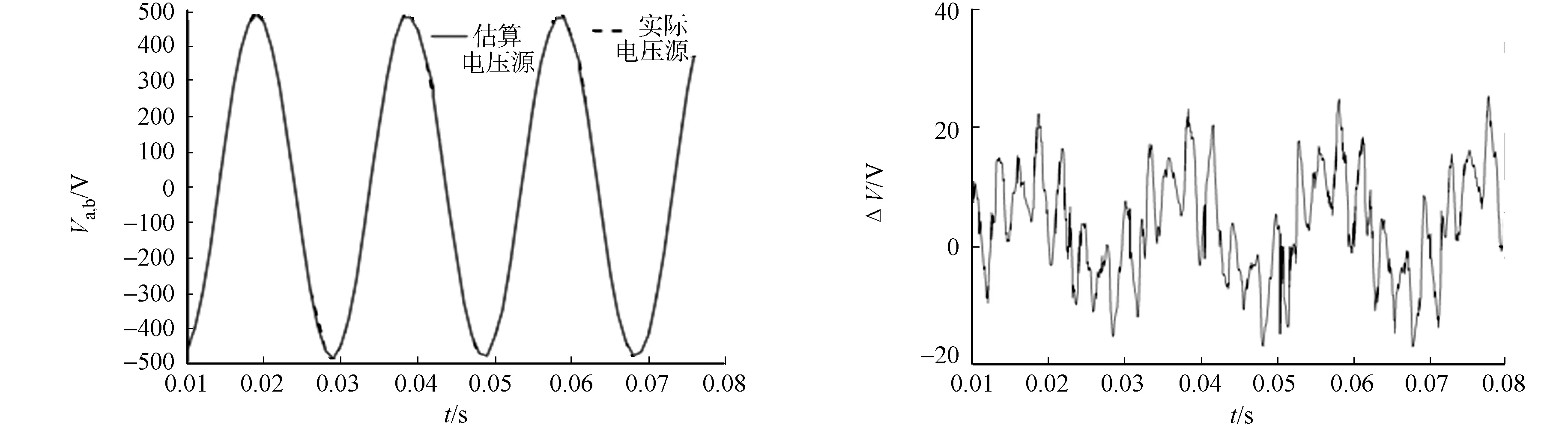
(a) 电压波形 (b) 匹配的误差图4 实际电压源与估算电压源的比较Fig.4 Comparison of actual voltage source and estimated voltage source

比例积分(PI)控制器和有限集模型预测控制器的比较，如图5所示.图5中：v为速度；Is为电机电流.已经使用Ziegler-Nichols法调整后者,并在调节器输出端添加一个低通滤波器解决机械共振.由图5可知：提出的方法表现出更好的动态响应.在稳态操作期间的输入相电流和电压，如图6所示.图6中：输出功率约为600 W.由图6可知：电流与其参考值非常匹配,与电压源同相，功率因数统一.结果显示低失真的正弦源电流，速度动态响应良好.此外,电动机端的电流表现良好，没有超过物理限制.当电机转速为500 rad·min-1时，电机输出电流波形，如图7所示.

(a) 速度 (b) 阶跃响应图5 PI控制器和有限集模型预测控制器的比较Fig.5 Comparison of PI controller and finite set model predictive controller

图6 电压源和电流源比较 图7 电机输出电流波形Fig.6 Comparison of voltage source and current source Fig.7 Output current waveform of motor

5 结束语

提出一种有限集模型预测控制算法，应用于矩阵变换器驱动的永磁同步电动机.提出的成本函数可以控制瞬态和稳态下的电流,避免在矩阵变换器输入端产生不稳定的振荡，实现电流限制,产生良好的速度动态响应.此外,提出一种新的输入滤波器观测器.估算电压源允许减少传感器的数量,可以提高整个系统的可靠性.通过实验测试对所提出的方法进行了验证,结果证实了提出的方法具备动态优势.

[1] AGUILERA R P,LEZANA P,QUEVEDO D E.Finite-control-set model predictive control with improved steady-state performance[J].IEEE Transactions on Industrial Informatics,2013,9(2):658-667.

[2] 沈坤,章兢,王坚.一种多步预测的变流器有限控制集模型预测控制算法[J].中国电机工程学报,2012,32(33):37-44.

[3] 朱晓雨,王丹,彭周华,等.三相电压型逆变器的延时补偿模型预测控制[J].电机与控制应用,2015,42(9):1-7.

[4] ROJAS C,RIVERA M,RODRIGUEZ J,etal.Predictive control of a direct matrix converter operating under an unbalanced AC source[J].International Symposium on Industrial Electronics,2010,10(2):3159-3164.

[5] RIVERA M,MUNOZ J,BAIER C,etal.A simple predictive current control of a single-phase matrix converter[J].Surgical Endoscopy,2013,27(3):235-239.

[6] ALESINA A,VENTURINI M.Analysis and design of optimum-amplitude nine-switch direct AC-AC converters[J].IEEE Transactions on Power Electronics,1989,4(4):101-112.

[7] XIA Changliang,ZHAO Jiaxin,YAN Yan,etal.A novel direct torque control of matrix converter-fed PMSM drives using duty cycle control for torque ripple reduction[J].IEEE Transactions on Industrial Electronics,2014,61(6):2700-2713.

[8] FUENTES E,KALISE D,RODRIGUEZ J,etal.Cascade-free predictive speed control for electrical drives[J].IEEE Transactions on Industrial Electronics,2014,61(5):2176-2184.

[9] 石宇静,李善强,武俊峰.具有执行器饱和与随机非线性扰动的离散系统模型预测控制[J].电机与控制学报,2014,18(8):99-104.

[10] 李宁,李颖晖,韩建定,等.基于混合逻辑动态模型的三相逆变电路有限控制集模型预测控制策略[J].电网技术,2014,38(2):375-380.

(责任编辑： 钱筠 英文审校： 崔长彩)

Current and Speed Control Technology of Permanent Magnet Synchronous Motor Driven by Matrix Converter

YU Haili1, WANG Jun2, SUN Wenlei3

(1. School of Engineering, Xinjiang Agricultural Vocational and Technical College, Changji 831100, China；2. School of Mechanical and Power Engineering, Nanjing University of Technology， Nanjing 211800, China;3. School of Mechanical Engineering, Xinjiang University, Urumchi 830047, China)

In this work, a finite set of model predictive control algorithm was proposed to solve the current and speed control problems of permanent magnet synchronous motor driven by the matrix converter,. Different from conventional matrix converter and control methods, the algorithm applied input filter cost function and the motor speed cost function and carried out the direct control under transient and steady-state conditions of the input current. In doing so, a high dynamic response was achieved and the voltage transients in variable filter input current induced by unnecessary vibration was avoided. In addition, a new input filter observer was developed to reduce the number of sensors, so as to increase the reliability of the system and reduce the cost. Finally, the effectiveness of the proposed algorithm was verified by simulation and experiments. Keywords： finite control set model； predictive control; matrix converter; permanent-magnet synchronous motor; cost function

10.11830/ISSN.1000-5013.201701003

2016-06-21

于海丽(1979-)，女，副教授，主要从事机械设计制造及其自动化的研究.E-mail:15528021@qq.com.

新疆维吾尔族自治区自然科学基金资助项目(2011211A002)

TM 341

A

1000-5013(2017)01-0013-06