基于OpenMP加速的无单元逆时偏移成像

周 震，贾晓峰

(中国科学技术大学 地球和空间科学学院，合肥 230026)

基于OpenMP加速的无单元逆时偏移成像

周 震，贾晓峰*

(中国科学技术大学 地球和空间科学学院，合肥 230026)

有限元法(FEM)和有限差分法(FDM)被用于求解地震波动方程，但该两种方法，在实际运用中，计算精度和效率会出现一些不足。事实上，无单元法(EFM)已经被用于地震波模拟和偏移成像，与FDM和FEM相比，EFM具有独特的优势：不需要事先划分大量网格，仅需要研究区域中节点和边界的信息，具有局部拟合的特点。但当前EFM处理地震波模拟和成像仍存在很多问题，如求取系数矩阵耗费过多计算机内存和计算量过大的问题。这里对系数矩阵采用按行压缩(CSR)的格式存储，并采用分步计算的策略。在时间递推过程中，求解线性方程组，为了提高计算效率，基于已有的FDM数据，利用OpenMP多核加速。通过上述方法，有效地解决了内存限制和计算效率的问题。数值算例表明，这里提出的方法是精确和高效的。

无单元法； 系数矩阵； 线性方程组； OpenMP； 逆时偏移

0 引言

在地震勘探领域，利用弹性波方程(近似为声波方程)描述物理震源在空间传播地震波场的过程，这是地震波方程正演和反演方法的物理基础。人们一直在探讨各种波动方程的数值解法，其目的是为了得到满意的地震波正反演结果。在这个过程中，不可避免的产生一些其他问题，比如数值算法的精度、计算机资源占用率、算法稳定性以及边界条件等。当前应用最广泛的数值计算方法为有限元法(FEM)和有限差分法(FDM)[3，8]，这两种方法发展较早且相对比较成熟。近年来，随着研究问题的深入和广泛，有限差分法和有限元法在计算精度和计算效率上出现了一些不足。

在岩石和工程力学领域中，发展起来的无单元法(EFM)已在地震勘探中获得有效的应用[7]。无单元法对于处理有限元法(FEM)中独立变量一次导数不连续、预处理较复杂等问题，具有良好的效果。同时利用滑动最小二乘法来拟合波场函数，使得EFM不仅继承了FEM的一些特点，更具有某些独特的优势:①无需事先划分单元，让EFM更具有灵活性，这使得在预处理时无需再去配置和组集单元，可有效降低工作成本；②EFM降低了构造形函数的难度，只需要考虑一个最小二乘的精度即可；③在EFM采用最小二乘拟合的思想，可获得高次连续解。

自2006年起，EFM首次被用于地震波模拟和成像，这次尝试为EFM在弹性波动方程中的应用奠定了基础。其中包括：①权函数的选择；②影响域的大小；③形函数的构造；④矩阵求逆的运算等。同时因为稀疏矩阵不恰当的存储问题，该方法在2G计算机内存的存储情况下，仅能处理81×81网格节点的模型，极大限制了EFM在较大速度模型中的应用，同时对于超大稀疏矩阵求逆，也是一项挑战。

通过对稀疏矩阵压缩处理，并将矩阵的求逆过程转化为求解线性方程组，Fan[4]解决了因稀疏矩阵不恰当存储所引起的存储瓶颈，同时通过‘PARDISO’ (Parallel Direct Sparse Solver)求解器[5]求解线性方程组，在计算精度得到保证的前提下，降低了计算成本。该方法对于节点和时间步长的选取，同样给出相应的解决方案。然而在计算效率方面，因为该方法在利用高斯积分计算刚度矩阵和质量矩阵时，采用了堆栈这一数据结构，该过程重复开辟内存存储空间，严重阻碍了计算效率。

作者在计算质量矩阵(M)和刚度矩阵(K)时，摒弃了借助堆栈的解决方案，改用数组存储中间稀疏矩阵，并对最终系数矩阵按行压缩存储(CSR)。在计算M和K的过程中，分两步进行：①在每一个高斯节点各自单独影响域内对模型节点计算出M和K，同时在计算过程中采用模型节点内层循环局部搜索代替全局搜索的策略，并利用相对坐标这一概念；②对不同高斯点影响域下包含的相同的模型节点上的M和K求和。其目的就是在不借助堆栈的情况下，利用有限的计算机内存，尽可能计算较大速度模型，从而为提高计算精度。

当求出M和K并压缩存储后，可通过隐式差分格式得到稀疏矩阵为系数的线性方程组。之后通过‘PARDISO’线性求解器求解。为了提高计算效率，利用已有的有限差分(FDM)程序，参考计算机的内核(CPU)个数，保存相应几个时刻的波场值及其对时间的一阶偏导。然后把已求值设为EFM中的起始点值，利用OpenMP-Fortran 编写并行程序，使得EFM在波场模拟和逆时偏移成像的过程中多核同时进行，进而提高计算效率。

1 无单元法基本理论介绍

考虑下面Ω研究区域，Γ为边界的二维标量波动方程为式(1)。

(1)

式中：u表示位移场；t表示时间坐标；x、y分别表示为空间上水平和竖直方向坐标；D表示介质中波速的平方。

假设u(x)为研究区域Ω上的场函数，各个模型节点上的值可表示为

u(xi)=uii=1,2,…,n

(2)

为了使用更加简单的形式求解方程，我们取其级数形式的近似解uh(x)

(3)

其中：pT(x)为m维基函数；m为基函数所含元素的个数。

当在二维情况下有：

一次基函数 pT(x)=[1,x,y]

(4)

二次基函数 pT(x)=[1,x,y,x2,xy,y2]

(5)

我们通过滑动最小二乘原理来确定a(x)。通过定义下面的泛函方程式，并求取泛函方程式的最小值：

(6)

其中：w(x-xI)为点x影响区域内的权函数其作用范围在有限区域内[4]。

为了求得a(x)，对式(6)的泛函方程式求极小值即

(7)

可得

a(x)=A-1(x)B(x)U

(8)

其中

(9)

B(x)= [w(x-x1)p(x1),w(x-x2)p(x2),

…,w(x-xNinf)p(xNinf)]

(10)

U=[u1,u2,…,uNinf]T

(11)

将a(x)带入方程(3)可得

uh(x)=p(x)A-1(x)B(x)U≡φ(x)U

(12)

其中：φ(x)称为形函数。

从方程(12)可知所得近似场函数，仅与基函数、权函数以及邻近点场值有关。

对方程(12)使用变分原理，即求解该方程等同于找出下面泛函的极小值：

(13)

其中a是罚因子。将近似解(12)代入(13) 并令求导为零，则可得：

(14)

式(14)中K、M和F分别表示为刚度矩阵、质量矩阵和载荷向量，其中K、M均为超大稀疏矩阵可用下面的表达式表示：

(15)

由公式(14)，可以得到如下方程组：

(16)

把平均加速法的隐式差分格式[7]应用到公式(14)，最终得到关于时间的递推公式：

(17)

当我们暂时不考虑边界条件时，载荷向量Fq可以忽略不考虑，通过前一时刻的波场值及其对时间的一阶偏导，联立方程组即可求得下一时刻的波场值和波场值对时间的一阶偏导。

2 无单元法中影响域的选择

在无单元法中，每个计算节点权函数的影响区域称为影响域，其选择会直接影响计算精度和计算工作量。影响域的选择要恰当，既不 能太小也不能太大：过小会使得滑动最小二乘法的解值不唯一；过大既偏离了无单元法中强调的局部拟合的特点，更会增加计算的工作量，加大计算成本。

考虑二维情况，并采用圆形影响域，则影响半径可定义为：

(18)

这里取β=4、m=6； d为节点密度，可定义为：

(19)其中：node为整个研究区域内节点总数；a、b分别为区域的长和宽；β是一经验常数，其大小可根据速度模型离散点间距大小而定，本文模型点间距为10 m～12.5 m，故β=4；m是基函数所包含的项数，因这里采用二次基函数即满足需求，故取m=6。

3 分步求取质量矩阵和刚度矩阵

无单元算法(EFM)中，刚度矩阵(K)和质量矩阵(M)是通过高斯数值积分计算得到的。其中K、M的计算和存储是限制EFM发展的瓶颈之一。为了解决内存限制并提高计算效率，采用分步求取K、M的策略：①在各自单独高斯节点影响域内对模型节点计算出K和M；②再对不同高斯点影响域内包含的相同的模型节点的K和M求和。有关分步计算K和M的过程可参考图1。

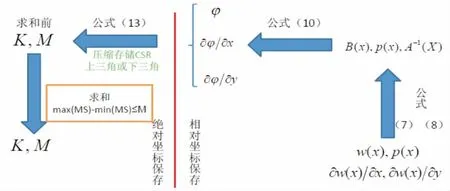
图1 分步计算K和M的流程图Fig.1 The flow diagram of computing K,M by multi-step

考虑到速度模型的特性(通常水平长度大于竖直深度)，为了便于后期求和，即让每个高斯点影响域内的模型点坐标值相差较小，我们把模型点按照自上而下，然后从左至右依次排序编号。此时在程序上，对于高斯点循环和速度模型离散点的两层循环要满足水平(X)方向在外，竖直(Y)方向在内的原则。

我们采用一种策略：让内层循环仅出现在相应高斯点影响域附近。考虑到高斯点的影响域是圆形，故可以做圆的外切正方形(图2(b))，使内层模型节点的循环仅出现在正方形区域内，让局部搜索循环替代之前的全局搜索循环。这样就保证了模型节点上的循环仅发生在影响域区域内及周围。即使随着模型的增大，内部的串行循环也不会有所增加，此策略下的串行循环只和高斯点区域大小和模型节点间的间距有关。

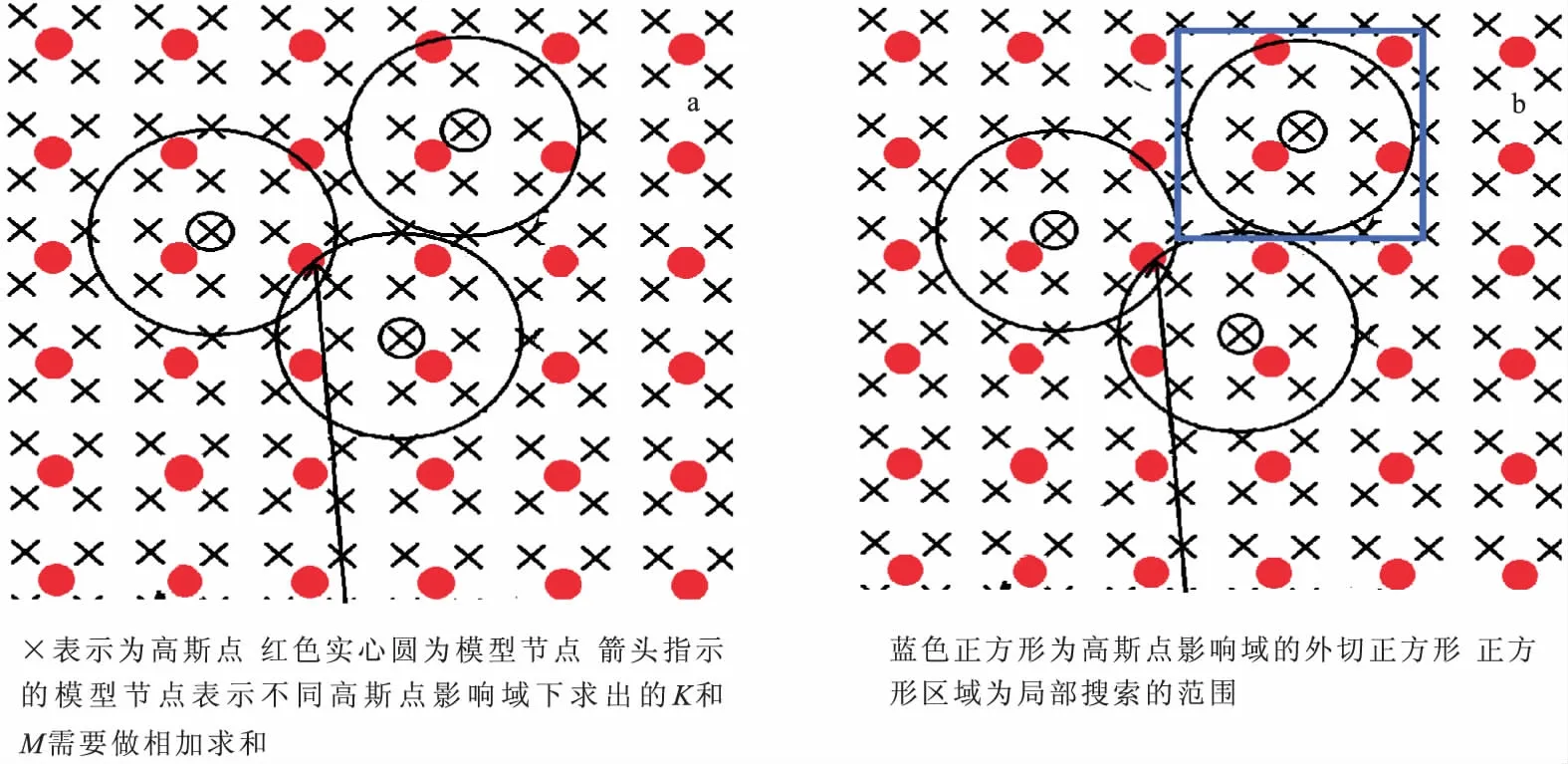
图2 不同高斯点对应的影响域范围和局部搜索示意图Fig.2 The figures of influenle domains of differnet Gauss points and loal search(a)不同高斯点对应的影响域范围图；(b)局部搜索示意图

考虑到B(x)、A(x)、p(x)是有关模型节点上的值，因此，它们必须和相应模型节点的坐标一一对应才会有意义。传统的方式是把上述三个待求矩阵内元素的坐标按照位于整个速度模型上的绝对位置，予以编号，然后赋予坐标值。这种方式有两个缺点；①用数组来保存时，消耗较大内存，并且极为稀疏；②参与下一步计算时，因为极为稀疏，所以耗时巨大。为了改变这一状况，把上述待求量在速度模型上的绝对坐标值，转换成每个影响域内的相对坐标。

考虑到二维模型上刚度矩阵和质量矩阵的物理含义，单独针对一个模型节点而言是没有意义的，而是应该考虑各个高斯点影响域内模型节点对模型节点的关系(图2(a))。又因为K、M均为稀疏对称矩阵，因此我们只需要求取上三角或者下三角矩阵即可。而对于K、M的坐标，则需要用基于整个速度模型的绝对坐标表示。

当求出每个高斯点影响域内的K、M后，因为CPU内存的限制，无法一次性把整个模型上不同高斯点影响域内包含相同模型节点处的值相加。从图2(a)中我们可以发现，因为每个高斯点的影响域是有限的，而待求和处的模型节点(不同高斯点影响域共有的模型节点)位于相应高斯点的附近，所以当把高斯点分块时，相应的待求和模型节点，也会被相应的分开。为了克服CPU存储空间的限制，分块后的高斯点应该满足下面的条件：分块后对应的模型节点的绝对坐标值(MS)满足max(MS)- min(MS)≤M(M是和CPU存储空间大小有关的整数，如CPU内存为2 GB时，M=6 561)。从图2(a)可知，邻近高斯点影响域总会有重合区域，即速度模型中的模型节点会属于邻近不同的高斯点影响域。为了得到最终的刚度矩阵和质量矩阵，需要把不同高斯点的影响域下包含的相同的模型节点的刚度矩阵和质量矩阵求和。

4 稀疏矩阵压缩存储

稀疏矩阵可定义为非零元素占全部元素的百分比很小(如5%以下)的矩阵。或者有的矩阵非零元素占全部元素的百分比较大(如近50%)，但它们的分布很有规律，利用这一特点可以避免存放零元素或避免对这些零元素进行运算。由于影响域通常是个较小区域(二维情形下包含十几个节点即可满足需求)，求出的K、M满足稀疏矩阵的定义。

稀疏矩阵的压缩方式有很多种，常用的是三元组方式，即用三个一维数组来表示稀疏矩阵，同时数组仅保存稀疏矩阵中的非零元素。这里采用按行压缩存储格式(CSR)。对于m×n(m行n列)具有q个非零元素的稀疏矩阵，应用CSR 格式存储时，使用的三个数组分别为：一个q×1维的值数组value，它按行序分成了m个段；一个q×1维的列下标数组column；一个(m+1)×l 维的数组row，该数组中的元素指向各段中首元素在稀疏矩阵中的顺序号。第i行非零元素的个数(row[i+1]-row[i])。

以文中的简单三层模型为例：对于(596×300)*(596×300)的双精度稀疏矩阵，按上三角或下三角保存的结果计算，保存在一维数组的元素个数小于10 000 000。如果采用一般方法全存储所需要的空间为：(596×300)*(596×300)*sizeof(float)*16/(1 024*1 024*1 024)=1 905.52 GB。而采用CSR上三角或下三角存储所需要的空间最大为10 000 000*sizeof(float)*16/(1 024*1 024*1 024)=0.6 GB。因此压缩存储所占全存储的比例小于0.6/1 905.52=0.032%。

有关CSR格式的压缩存储情况参见表1。

表1 稀疏矩阵C的CSR格式压缩存储形式为(按行优先)
Tab.1 The CSR format of the sparse matrixC(priority by row)

1-basedindexingvalue1-1-3-25464-4278-5row14691214column1231234513425

其中：value为稀疏矩阵中包含的非零元素值；row为每一行第一个非零元素在value中的起始偏移位置；column为非零元素值对应的列标。

1)在程序中，我们采用1-based设置 indexing。需要注意的是：最后一行最后一个非零元素在value的排列位置再加“1”，则为row中最后一个元素值。

2)实践证明，选择CSR格式较好，理由是CSR存储格式，不仅相对来说占用较少内存，同时对于后面涉及到的矩阵向量相乘，以及解线性方程组，效率更高。主要原因是矩阵向量相乘本身的运算规则，使得CSR存储格式更占优势。同时有关MKL的库函数对于CSR格式的存储，在做矩阵向量相乘时，包含有并行的思想。

5 基于OpenMP 对时间递推的多核加速

叠前偏移可以作用于任意非层状速度模型，叠前偏移主要是利用共反射点反射波的叠加。有关叠前偏移成像通常是分别计算单炮炮点正传时的波场函数和反传时检点数据延拓的波场函数，然后利用成像条件，即可得到地下结构的成像。这里将采取叠前偏移，同时利用互相关成条件。零延迟互相关成像条件的表达式为：

(20)

其中：tmax为最大记录时间；S(x,t)为正传的震源波场；R(x,tmax-t)为检点数据反传的接收场；I(x,t)为x处的成像结果。

将时间递推公式(17)转化成线性方程组可得式(21)。

(21)

M、K，待求解线性方程组的系数矩阵分别为M+((Δt)2/4)K、M。

在做矩阵向量相乘时，利用 Sparse BLAS 库函数，其调用语句为：

Call mkl_dcsrsymv (uplo,m,a,ia,ja,x,y)

其中各个参数含义如表2所示。

在波场模拟和逆时偏移成像过程中，把原来需要对稀疏矩阵求逆的方程组转化成线性方程组，并采用‘PARDISO’ 线性求解器求解。考虑到在每一个时间迭代步中需要做三次矩阵向量相乘和求解两次线性方程，即使K、M是压缩存储以后的，该过程仍需要消耗大量的时间。为了提高计算效率，我们利用已有的FDM程序，计算并均匀保存8个时间点处的波场值及其对时间的一阶偏导数(考虑到服务器为8核CPU)。

表2 调用矩阵向量相乘各个参数的含义

Tab.2 The meaning of each parameter of calling matrix vector to multiply

输入参数uplouplo=‘U’或‘u’表示为a只保存对称矩阵的上三角;uplo=‘L’或‘l’表示为a只保存对称矩阵的下三角;m整型。表示为稀疏方阵A的行或者列a双精度型。表示为稀疏矩阵A按CSR格式压缩存储后的value向量ia整型。表示为稀疏矩阵A按CSR格式压缩存储后的row向量ja整型。表示为稀疏矩阵A按CSR格式压缩存储后的column向量x双精度型。表示为已知被乘的向量,且包含m个元素输出参数y双精度型。表示为待求的向量,且包含m个元素

假设波场模拟的总时间为T，首先利用FDM程序，求出完整的波场正传和反传值，并保存波场正传和反传时T/8，2T/8，…，7T/8时刻的波场及一阶偏导值；之后以此为基准点值，即作为EFM中的起始值，这样8个时间段内的时间递推即可在OpenMP程序中同时进行。理论上，8个时间段内的时间递推同时进行，可使效率提高到8倍左右，但实际上并非如此。主要原因是在利用Sparse BLAS 库函数执行矩阵向量相乘和‘PARDISO’求解线性方程组的过程中，所调用的函数本身是多核并行的，以Marmousi模型为例，在调用这两个函数时，CPU利用率约为300%，同时内存占用率约为20%(总内存为30 G)。综合考虑，我们一次并行的数量可选取4个时间段。这样理论上应该获得8/3倍的加速，算例表明通过OpenMP，加速率约为2.5倍，与理论加速比基本吻合。

OpenMP编译器命令以！$OMP parallel/!$OMP end parallel定义一个并行域[6]，并利用OpenMP函库中的OMP_get_num_process( )函数，获得CPU核的个数，根据前面讨论的4段并行，确定线程数目(call OMP_set_num_threads(4))。并行部分程序流程见图3，其中红绿色箭头表明计算过程有先后之分。

在编写OpenMP并行程序时，特别需要注意在实现并行后，循环内部所有变量根据具体情况，开辟为与循环维度和次数相关的数组。每个循环内部的变量必须独立于其他循环，只被该循环修改，不受其他任何循环的影响。对于各循环共同读取但不修改的变量，可以不必定义(扩充)为数组。调试并行程序中对那些非数组变量一定要小心谨慎，确保其在循环中始终为某一常量，否则就会出现错误。并行后的程序需满足以下原则：该循环内部的所有变量，在任何情况下都不会被任何其他循环修改。

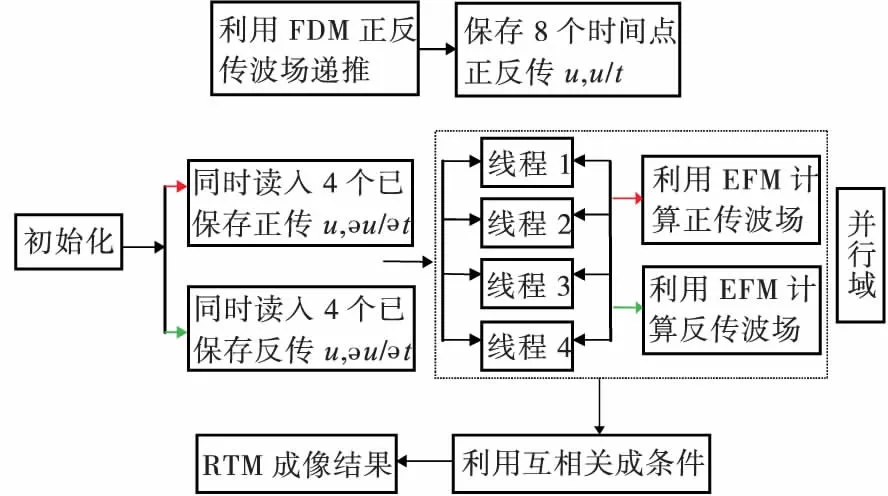
图3 并行程序流程图Fig.3 The flow diagram of parallelism

6 数值算例

6.1 水平层状介质模型

为了有效说明本文算法及改进的合理性，先测试一个简单模型：水平三层介质模型(图4)，该模型研究区域水平方向长为7.4 375 km，竖直方向深度为2.99 km，模型节点数为596×300。三层速度自上而下依次为2.5 km/s、3.5 km/s、4.5 km/s。采用3×3阶次的高斯积分，高斯网格数为300×300。权函数为幂权函数，震源是主频为25Hz的高斯子波，总记录时间为3 s，时间间隔为1 ms。从图5和图6可以看出，得到利用FDM数值，基于OpenMP-Fortran编写的并行EFM程序，对于三层简单模型的RTM单炮和多炮叠后成像。图7 表示基于FDM 20炮RTM叠加后的成像图。由成像结果可知，改进后EFM算法得到的成像精度与FDM成像精度是吻合的。

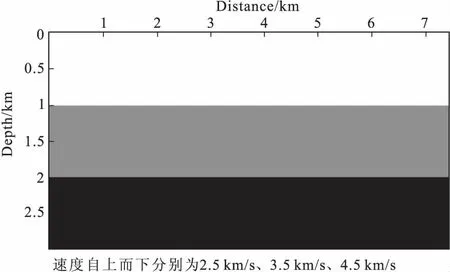
图4 水平三层介质速度模型Fig.4 The three-layer velocity model

图5 单炮利用无单元法RTM成像结果Fig.5 The single-shot images obtained by the EFM (based on FDM and OpenMp) RTM

有关图6、图7分界面附近的干扰是因为采用双程波动方程RTM引起的，图6相比于图7可发现无单元RTM结果的同相轴更细，主要原因是无单元的浅层噪音相关性较差，叠加干涉的效应在横向上的规律不明显，客观上避免了因强烈的干涉导致子波展宽的现象发生；而差分的浅层噪音相关性较好，叠加干涉后顶点能量加强并对反射界面主能量有展宽效应。

图6 利用无单元20炮RTM叠加后的成像结果Fig.6 The stacked image from 20 single-shot images obtained by the EFM (based on FDM and OpenMp) RTM

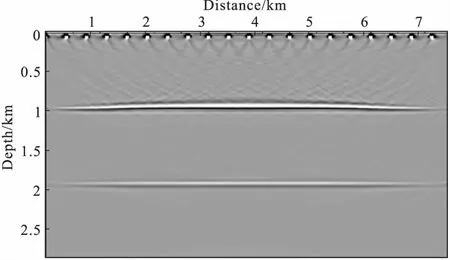
图7 利用有限差分法20炮RTM叠加后的成像Fig.7 The stacked image from 20 single-shot images obtained by the finite difference RTM

6.2 Marmousi模型

图8为Marmousi模型。该模型长为7.425 km，深度为2.99 km。把Marmousi模型离散为595×298个模型节点，仍然采用采用3×3阶次的高斯积分，300×300高斯网格数，震源是主频为25 Hz的高斯子波，总记录时间为3 s，时间间隔为1 ms。利用已有FDM数值做EFM起始数值和OpenMP-Fortran编写的并行程序。图9 (a)、图9 (b)、图9 (c)、图9 (d)、图9 (e)分别表示基于OpenMP-Fortran并行的无单元算法在0.6 s、0.8 s、1.0 s、1.3 s、1.7 s的波场快照。图10表示基于OpenMP-Fortran并行EFM 18炮RTM叠加后的成像图。从图10中可以看出，Marmousi模型中三个高角度逆掩断层、断层下面的盐丘、以及深部两侧的高速体都得到很好的成像，结构清晰，位置精确。图11为基于FDM 18炮RTM叠加后的成像图。从表3、图10、图11与图12可知，和传统无单元算法相比，在分步求取K、M时，对模型节点的内层循环采用不同的搜索方式，对于效率的提升有明显的影响；同时借助已有的FDM程序计算结果，通过OpenMP多核加速，所得成像结果是可信的，且精度在可接受范围内。

图8 Marmousi速度模型Fig.8 Marmousi velocity model

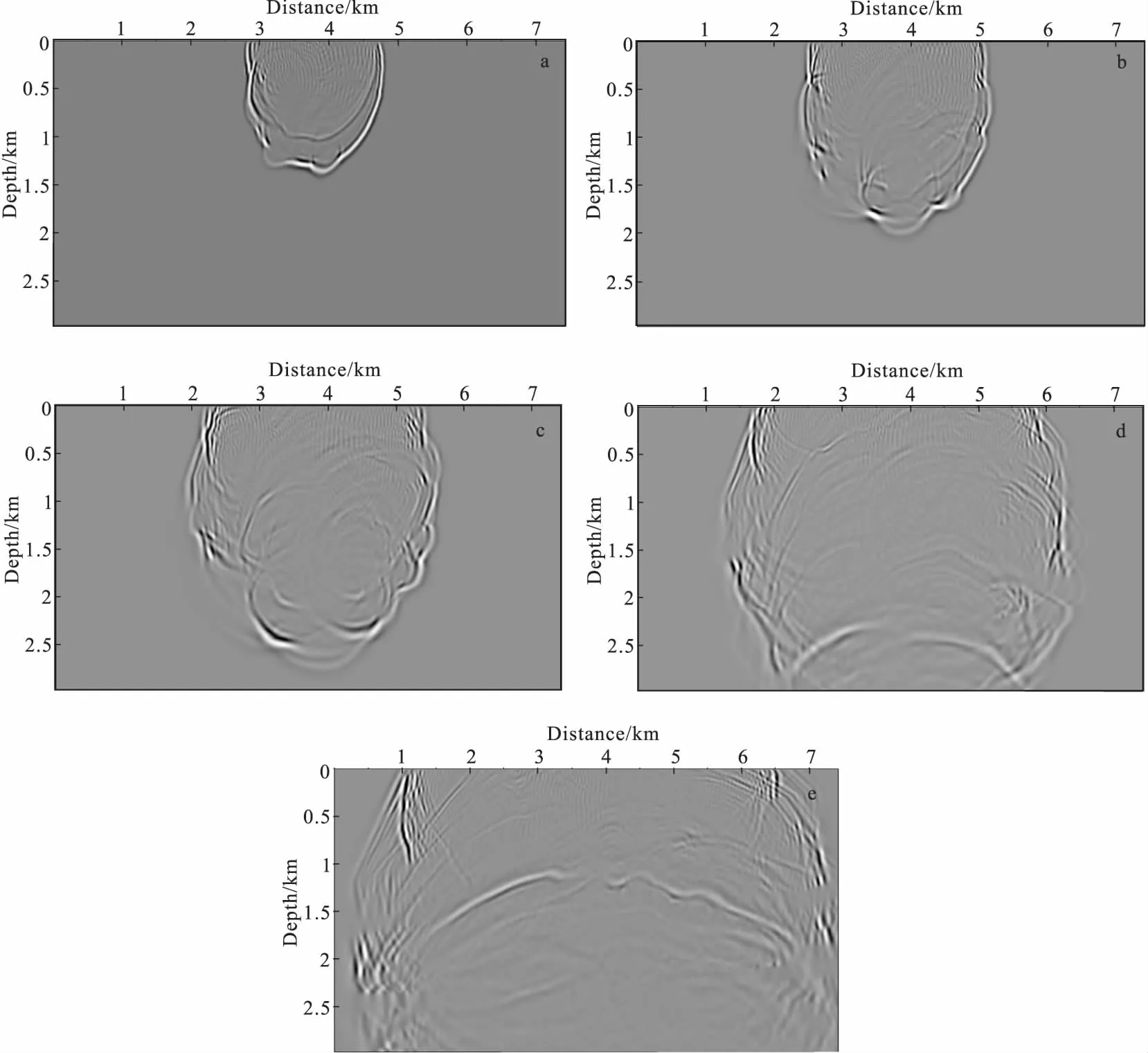
图9 无单位法(基于FDM数据做OpenMp多核加速)在炮点位于(100 m，3737.5m)对应的0.6 s,0.8 s,1.0 s,1.3 s,1.7 s的波场快照Fig.9 Snapshots simulatcd by the EFM (based on FDM and OpenMp)in Marmousi model(a)0.6 s时的波场快照；(b)0.8 s时的波场快照；(c)1 s时的波场快照；(d)1.3 s时的波场快照；(e)1.7 s时的波场快照；

图10 利用无单元法18炮RTM叠加后的成像Fig.10 The stacked image from 18 single-shot images obtained by the EFM (based on FDM and OpenMp)

图11 利用有限差分法18炮RTM叠加后的成像Fig.11 The stacked image from 18 single-shot images obtained by the finite difference RTM

K,M计算时间/min 模拟时间/minRTM成像时间/min传统EFM420520620改进后EFM(全局搜索求K,M+OpenMp)5595135改进后EFM(局部搜索求K,M+OpenMp)94989计算耗时比(传统EFM:全局搜索求K,M+OpenMp)7.635.474.59计算耗时比(传统EFM:局部搜索求K,M+OpenMp)46.6710.616.97

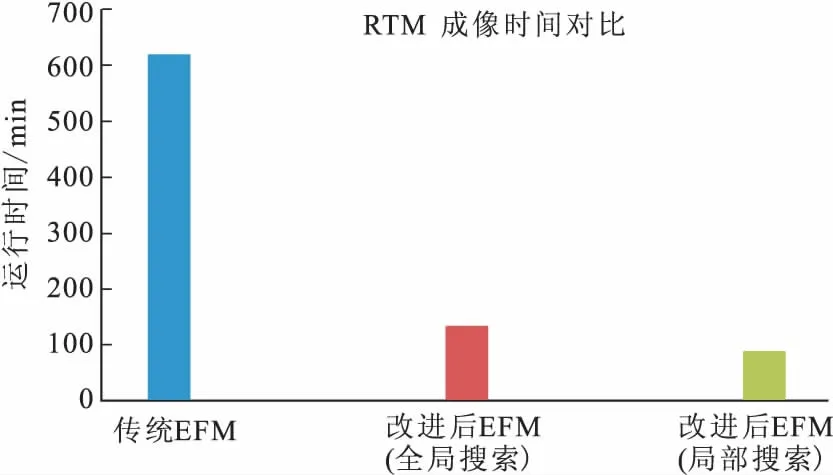
图12 Marmousi模型RTM计算效率比较Fig.12 The comparison of computation efficiency of RTM in Marmousi

7 结论

研究的主要内容为分步计算无单元算法中的刚度矩阵和质量矩阵，并借助已有的有限差分程序的计算结果，利用OpenMP在时间递推过程中多核加速。在地震波模拟和成像中的应用，无单元算法一直存在的两个问题：①计算机内存的限制；②计算效率不高的问题。通过分布计算K、M解决内存的瓶颈，同时提高了计算K、M的效率，并通过多核加速提升时间递推过程的计算效率。

在分步计算K、M时，采用局部搜索内层模型节点循环替代全局搜索，并把计算所得的K、M按行压缩存储(CSR)。考虑到K、M的对称性，只保存上三角(或者下三角)。同时需注意在求取的第二步，即求和的过程，要根据计算机的内存，把高斯点相应分块处理去做求和，直到整个速度模型上所有高斯节点坐标不同但模型节点坐标相同的值求和完毕为止。转化为线性方程组，避免了对超大稀疏矩阵求逆，通过‘PARDISO’线性求解器，可以有效解决问题。当使用OpenMP 做基于CPU多核并行计算时，程序中静态数组仅能支持小数组(比如一维数组最大为1000000)，当数组较大时，程序中应使用动态数组。

数值算例表明，改进后的无单元算法在满足计算精度的前提下，计算效率有了很大地提升。这为计算更大的速度模型和三维速度模型提供了可能。同时文中的这些改进措施同样可用于有限元(FEM)问题的求解。当然在计算效率方面，无单元法和有限差分法相比，还是存在很大差距，提升空间巨大。

关于未来的工作，我们可以有以下几个方面的展望：

1)可研究类似小波变换等算法，对质量矩阵和刚度矩阵进行数据压缩存储，在可行的压缩率和压缩质量下，可以有效地减少空间存储和提高计算效率。

2)有关求取刚度矩阵和质量矩阵可考虑移植到GPU平台计算。

3)在二维无单元算法的基础上，把无单元算法推广到三维空间。

4)把时间域的无单元算法，推广到频率域。因为单个频率间是相互独立，频率域无单元算法更加适合做并行计算。

[1]BELL N,GARLAND M.Efficient sparse matrix-vector multiplication on CUDA[R].Nvidia Technical Report NVR-2008-004,Nvidia Corporation,2008.

[2]BELYTSCHKO,T.,LU,Y.Y,et al.Element-free Galerkin methods:Int.J.Numer[J].Methods Eng，1994,37:229-256.

[3]CLAERBOUT,J.Toward a unified theory of reflector mapping[J].Geophysics,1911,36:467-481.

[4]Fan,Z,JIA,X.Element-Free Method and its Efficiency Improvement in Seismic Modeling and Reverse Time Migration[J].Geophys.Eng,2013,10(2):1-12.

[5]GOULD N I M,HU Y,SCOTT J A.A numerical evaluation of sparse direct solvers for the solution of large sparse,symmetric linear systems of equations Technical Report[R].Numerical Analysis Internal Report 2005-1,Ruther ford Appleton Laboratory,2005.

[6]HERMANNS M.Parallel Programming in Fortran 95 Using OpenMP[D].Universidad de Madrid,2002.

[7]JIA,X,HU,T.Element-free precise integration method and its applications in seismic modelling and imaging[J].Geophys,2006,166(1):349-372.

[8]MARFURT,K.J.Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J].Geophysics,1984,49:533-549.

[9]KRYSL P,BELYTSCHKO T.Element-free Galerkin method:Convergence of the continuous and discontinuous shape[J].Computer methods in applied mechanics and engineering,1997,148(3):257-277.

[10]LU,Y.Y.,BELYTSCHKO,T.Tabbara,M.Element-free Galerkin method for wave propagation and dynamic fracture[J].Comput.Methods Appl.Mech.Engrg,1995,126:131-153.

[11]LU Y Y,BELYTSCHKO T,TABBARA M.Element-free Galerkin method for wave propagation and dynamic fracture Comput[J].Methods Appl.Mech.Eng,1995,126 :131-53.

[12]冯英杰,杨长春,吴萍.地震波有限差分模拟综述[J].地球物理学进展,2007,22(2):487-491.FENG Y J,YANG C C,WU P.The review of the finite-difference elastic wave motion modeling [J].Progress in Geophysics,2007,22(2):487-491.(In Chinese)

[13]纪国良,冯仰德.大规模有限元刚度矩阵存储及其并行求解算法[J].数值计算与计算机应用,2012,33(3):230-240.JI G L,FENG Y D.Parallel solving large-scale linear system of FEM based on compressed storage format [J].Journal on Numerical Methods and Computer Applications.2012,33(3):230-240.(In Chinese)

[14]贾晓峰,胡天跃,王润秋.复杂介质中地震波模拟的无单元法[J].石油地球物理勘探,2006,41(1):43-48.JIA X F,HU T Y,WANG R Q.A mesh free algorithm of seismic wave simulation in complex medium [J].Oil Geophysical Prospecting,2006,41(1):43-48.(In Chinese)

[15]阎树文.无单元法用于高分辨率地震模拟与成像[D].合肥：中国科学技术大学,2010.YAN S W.Element-free method applied in seismic modeling and imaging in high-resolution[D].Hefei：University of Science and Technology of China,2010.(In Chinese)

[16]杨顶辉.双相各向异性介质中弹性波方程的有限元解法及波场模拟[J].地球物理学报,2002,45(4):575-583.YANG D H.Finite element method of the elastic wave equation and wavefield simulation in two-phase anisotropic media [J].Chinese J.Geophys,2002,45(4):575-583.(In Chinese)

[17]姚松,田红旗.有限元刚度矩阵的压缩存贮及组集[J].中南大学:自然科学版,2006,37(4):826-830.YAO S,TIAN H.Compressed storage scheme and assembly procedure of global stiffness matrix in finite dement analysis [J].Journal of Central South University:Natural Sciences,2006,37(4):826-830.(In Chinese)

[18]张湘伟,蔡永昌.一种改进的无单元[J].计算力学学报,2002,19(1):26-30.ZHANG X W,CAI Y C.An improved element free method [J].Chinese Journal of Computational Mechanics,2002,19(1):26-30.(In Chinese)

[19]周小平,周瑞忠.无单元法研究现状及展望[J].工程力学,2005,22(1):12-20.ZHOU X P,ZHOU R Z.Current Study and development of Element-Free Galerkin method [J].Engineering Mechanics,2005,22(1):12-20.(In Chinese)

OpenMP-accelerated element-free reverse-time migration

ZHOU Zhen,JIA Xiao-feng*

(School of Earth and Space Science,University of Science and Technology of China,Hefei 230026,China)

The wave-equation-based method was widely used in seismic modeling and imaging in the past years.Many numerical strategies such as the finite element method (FEM) and the finite difference method (FDM) are developed in solving seismic wave equations.However,both methods have some shortcomings of either accuracy or computational cost in practice.In fact,element-free method (EFM) has been applied in seismic modeling and seismic migration imaging.Compared with FEM and FDM,EFM has unique advantages:it doesn't need to be divided a large number of grid in advance and it satisfies local fitting because only the information of the nodes and the boundary of the study area are required in computation.However,there are many problems that EFM is applied in seismic modeling and seismic migration imaging in present,e.g.the problems of storage and computation efficiency about computing the coefficient matrix.The storage is caused by improper storage of sparse coefficient matrix.In this paper we compress the sparse matrices by the compressed sparse row (CSR) format and employ the following strategy:firstly,the value is computed at the corresponding model nodes within the influence domain of each Gauss point; secondly,the summation is performed within the influence domain of different Gauss points that contain the same model node.In the calculation of wave field time recursive,we solve the linear equations with the help of linear sparse solver 'PARDISO'.In order to further improve the computation efficiency,we use OpenMP basing the existing FDM data.Through the above methods,we can effectively solve these problems of memory limit and computational efficiency.The final results indicate that the above methods are accurate and efficient.

element-free method； coefficient matrix； linear system of equations； OpenMP； reverse time migration

2015-10-08 改回日期：2015-11-26

国家自然科学基金(41374006，41274117)

周震(1986-)，男，硕士，从事地震波偏移成像和并行加速研究，E-mail：zzhen12@mail.ustc.edu.cn。

*通信作者：贾晓峰(1979-)，男，副教授，主要从事地震波场的数值模似和偏移成像，Email:xjia@ustc.edu.cn。

1001-1749(2016)06-0821-11

P 631.4