随机介质模型中瑞雷波正演模拟及波场特性分析

赵宏欣，熊章强,b，张大洲,b

(中南大学 a.地球科学与信息物理学院,b.有色金属成矿预测教育部重点实验室,长沙 410083)

随机介质模型中瑞雷波正演模拟及波场特性分析

赵宏欣a，熊章强a,b，张大洲a,b

(中南大学 a.地球科学与信息物理学院,b.有色金属成矿预测教育部重点实验室,长沙 410083)

为了研究介质的不均匀性对瑞雷波波场特性的影响，利用高精度交错网格法对不同自相关长度的随机介质模型在不同震源主频率时的波场进行了正演模拟，并应用相移法提取了频散曲线。通过对比波场快照、单道记录及分析频散曲线可以得出：随机介质中的不均匀体会导致瑞雷波传播能量的减弱，并使波的到达时间发生变化；大于或与波长相当的不均匀体随机介质以及由细密薄层构成的地层介质对频散曲线影响较大，这种情况下进行瑞雷波勘探时不能将其视为均匀介质。

随机介质； 瑞雷波； 频散曲线； 波场特性

0 引言

瑞雷波所具有的频散特性，使得通过提取其频散曲线可反演得到地下的地质体结构。由于这种勘探方法对浅部地质体的勘探精度较高，数据采集和处理简单高效，因而被广泛应用于工程地质勘查和工程质量检测等领域[1-2]。目前，瑞雷波在正反演理论、频散曲线提取及反演和应用等方面，均做了大量的研究工作。但在某些方面的研究工作还不够深入，如利用瑞雷波方法对混凝土进行质量检测时是否要考虑介质的非均匀性就有待进一步研究，在对这种介质的非均匀性进行研究过程中引入随机介质模型就是一种行之有效的手段。

在随机介质中进行地震波传播特性的研究，国内、外学者已开展过相关的工作。Ikelle等[3]介绍了二维随机介质的构建方法，并讨论了随机介质中透射波场的特性；Tobias 等[4]应用格林函数构造二维和三维随机介质模型；奚先和姚姚[5-9]介绍了混合型随机介质模型的构建方法，并研究了随机介质中波场特性和能量特性；王慧琴等[10]研究了二维随机介质中的频谱特性和能量分布的特点；朱生旺等[11]用随机介质模型的方法描述了孔洞型油气储层的问题，取得了很好的效果。以上研究工作，主要针对随机介质中地震体波传播特性，而有关瑞雷波在随机介质中的传播特性研究相对较少，肖云飞等[12]研究了瑞雷波能量在水平和垂直传播方向上的衰减及震源埋深对瑞雷波能量的影响。就瑞雷波而言，其频散曲线的特性是瑞雷波应用的关键所在。基于以上原因，这里运用高斯自相关函数构建随机介质模型，利用高精度交错网格法进行正演模拟，分析采用不同自相关长度的随机介质模型对瑞雷波传播特征及频散曲线特征进行研究，为可否利用瑞雷波方法进行复杂介质地探测提供理论参考。

1 理论原理

1.1 波动方程

波场模拟使用交错网格有限差分法，一阶速度-应力弹性波动方程如下：

(1)

其中：Di表示i方向上的差分；λ与μ为拉梅常数；“·”表示该变量对时间t的一阶导数，吸收边界与自由边界条件参考文献[13] 。

1.2 震源函数

这里选用的震源子波函数为高斯一阶导数，其表达式为：

s(t)=-4π2f2(t-t0)e-2π2f2(t-t0)2

(2)

其中：t0为延迟时间；f为震源子波频率。

图1(a)、图1(b)分别为f=2 500 Hz时的震源子波波形图及其振幅谱图。

1.3 随机介质模型的建立

复杂非均匀介质中的非均匀体可以看成一个空间随机过程，将这些具有大量的、随机分布的、小尺度异常的复杂非均匀介质看作随机介质，利用统计学方法描述介质非均匀性所形成的非均匀介质模型就是随机介质模型。随机介质模型由均匀性的大尺度和非均匀性的小尺度二部分构成，大尺度描述背景介质的情况，小尺度则是加在背景介质上的随机扰动。

各向同性弹性介质由其密度ρ和拉姆参数λ、μ所确定,介质中相应的纵横波速度如式(3)所示。

(3)

故各向同性弹性介质可以由Vp、Vs、ρ表示。同理，随机介质模型也可以用Vp、Vs、ρ来表示。在这里假设纵波速度Vp、横波速度Vs的相对扰动是相同的，密度ρ的相对扰动与其是成线性的，则可以用一个参数σ表示相对扰动，见式(4)。

(4)

其中：Vp0、Vs0、ρ0为大尺度的背景介质参数；k为常数，一般取值在0.3～0.8，这里取值为0.5。

设相对扰动σ是具有零均值及一定自相关函数、方差的空间二阶平稳随机过程。这里的相对扰动σ由高斯型自相关函数φ(x,z)生成。

(5)

其中：α和β分别为x和z方向上的自相关长度。

选取高斯型自相关函数，运用以上所描述的方法构建随机介质模型，分别选取自相关长度为：α=1、β=1；α=100、β=1；α=100、β=100；α=5 000、β=1。型拟网格数为200*200，背景介质参数为：Vp=3 000 m/s；Vs=1 800 m/s；ρ=2.5 g·cm-3。图2为所建立的四种随机介质模型。

图2中α和β分别代表x和z方向上的自相关长度，通过改变α、β的大小来控制随机模型中随机异常体尺度的大小。从图2可以看出：当α和β较小时，随机异常体的尺度也相对较小；随着α、β的增大，随机异常体的尺度也相应增大。单独改变一个方向的自相关长度时，随机模型在自相关长度改变的方向发生变化，同时增大自相关长度α、β时，随机模型中随机异常体呈现单尺度增大。随机介质模型图2(a)和图2(c)由不同大小随机异常体构成，且随机异常体的尺度逐渐增大，可以刻画由不同颗粒所组成的地层介质或由不同颗粒的掺和物组成的混凝土等；随机介质模型图2(b)和图2(d)沿x方向成连续状，并呈现出薄层状特征，此时可以刻画由不同薄层组成的地层介质如砂、泥岩等。

图1 震源子波波形与振幅谱图Fig.1 The figure of waveform and amplitude spectrum(a) 波形图；(b)振幅谱图

图2 不同自相关长度的随机介质模型图Fig.2 Random medium model of different autocorrelation lengths(a)α=1,β=1;(b)α=100,β=1;(c)α=100,β=100;(d)α=5 000,β=1

2 随机介质模型中瑞雷波场特性分析

为了对比分析随机介质中瑞雷波传播特性和频散曲线特征，特设计一个网格数为200*200的模型，其参数为：背景场Vp=3 000m/s、Vs=1 800 m/s、ρ=2.5 g·cm-3，及随机异常体尺度逐步增大及逐步呈薄层的七种自相关长度的随机介质模型，分别为：α=1、β=1；α=50、β=50；α=100、β=100；α=1 000、β=1 000；α=100、β=1；α=1 000、β=1；α=5 000、β=1。利用高精度交错网格有限差分法对七种随机介质模型进行正演模拟，震源主频率分别设为500 Hz、1 000 Hz、2 500 Hz，道间距为0.04 m，采样间隔为0.004 ms，采样点数为1 500。

从图3～图5可以看出，地震波在随机介质模型中传播时，纵波、横波和瑞雷波都有散射现象存在。从图3中可见，震源主频率为500 Hz时，随机介质模型中散射波相对较弱。随着震源主频率增大为1 000 Hz、2 500 Hz 时，散射波逐渐加强，且更加细微，这说明震源主频较小即波长较大时，随机介质模型中颗粒较小的随机异常体或薄层对地震波散射较弱。对比图3～图5的(a)、(b)波场快照可以看出，随着自相关长度α、β的同时增大，地震波的散射程度也相应地增大，且散射很明显；对比图3～图5中的(c)、(d)波场快照可见，随着x方向上的自相关长度α的增大，散射相对较弱，但层间反射逐渐明显，这是由于随着自相关长度α的增大，模型逐渐趋向于层状模型的原因。

在分析了波场快照后，分别选取网格数为200*200的均匀介质模型及自相关长度分别为α=1、β=1；α=50、β=50；α=100、β=100；α=100、β=1；α=1 000、β=1的随机介质模型正演，震源主频为2 500 Hz，震源位置(100,0)，道间距为0.04 m，采样间隔为0.004 ms，采样点数为1 500，抽取第150道数据进行对比分析，如图6(a)、图6(b)所示。从图6(a)、图6(b)可以看出，随机介质模型中瑞雷波能量有所减小，时间有所延迟，但波形与均匀介质中的记录基本一致，在曲线尾部出现的震荡，正是由于随机介质中的不均匀体对弹性波产生散射所致，但能量相对瑞雷波小。图6(c)、图6(d)为图6(a)、图6(b)所示地震记录的频谱，由图6(c)、图6(d)中可以看出，随机介质模型中地震记录的频谱波动较大，尤其在主频段。

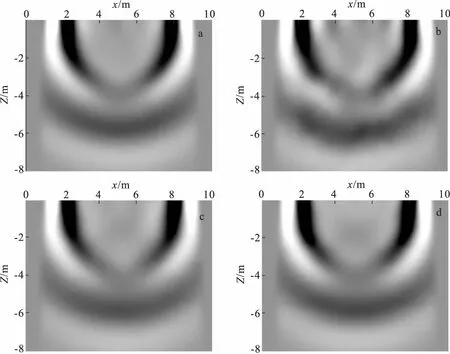
图3 震源频率为500 Hz的波场快照Fig.3 Wave field snapshot of 500 Hz(a)α=1,β=1；(b)α=100,β=100 ；(c)α=1 000,β=1；(d)α=5 000,β=1

图4 震源频率1 000 Hz波场快照Fig.4 Wave field snapshot of 1 000 Hz(a)α=1,β=1；(b)α=100,β=100；(c)α=1 000,β=1；(d)α=5 000,β=1

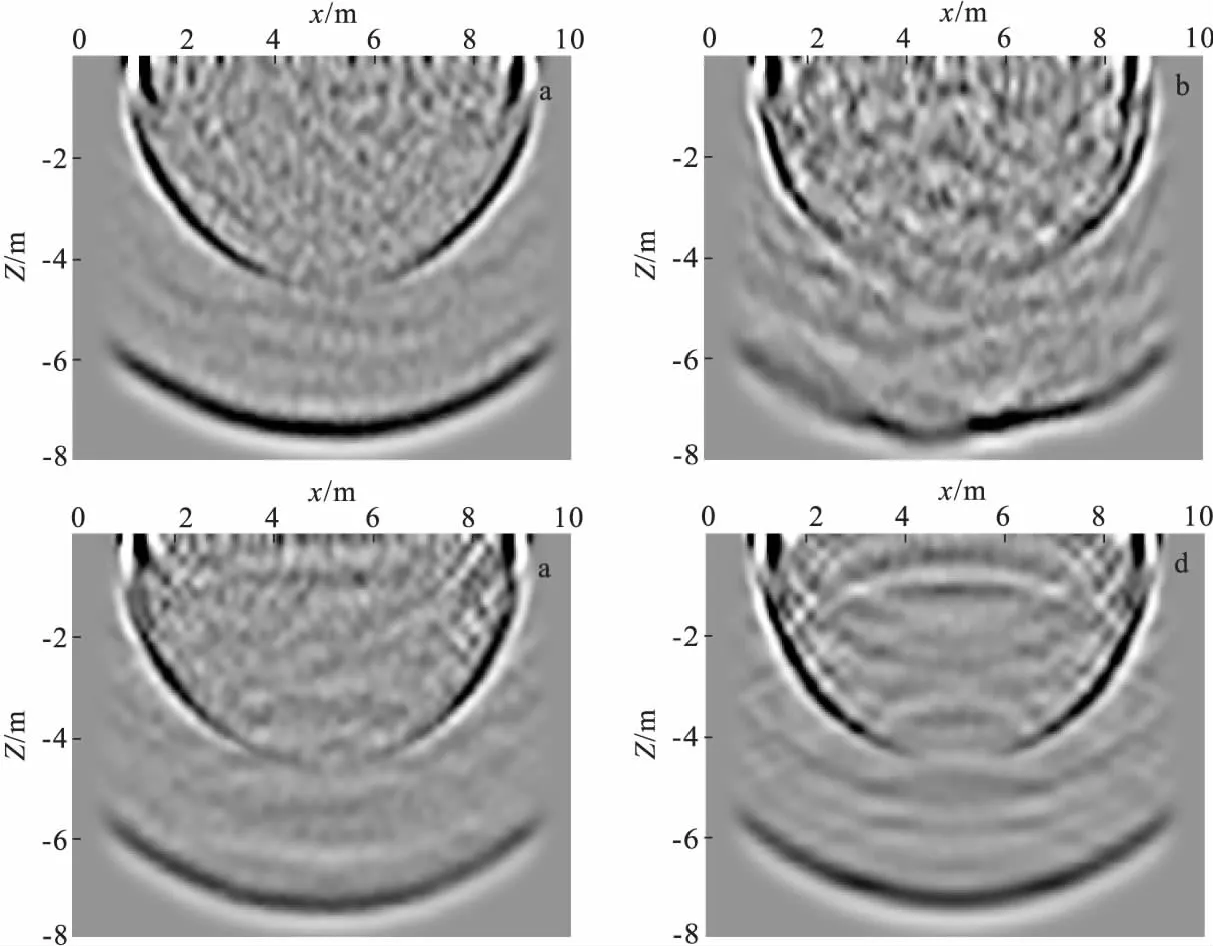
图5 震源频率2 500 Hz波场快照Fig.5 Wave field snapshot of 2 500 Hz(a)α=1,β=1；(b) α=100,β=100；(c)α=1 000,β=1；(d)α=5 000,β=1

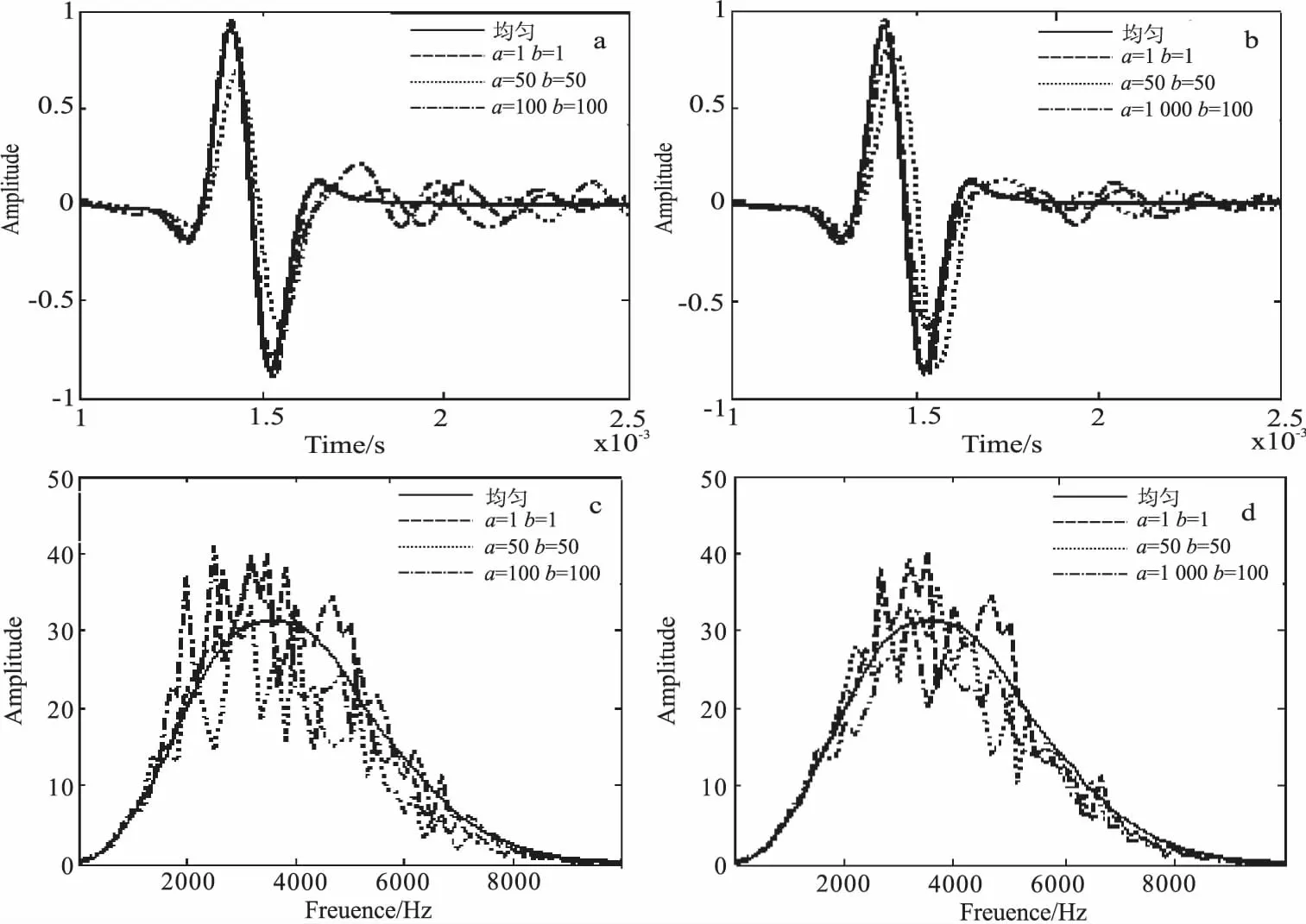
图6 波形与振幅谱对比图Fig.6 Comparison figure of waveform and amplitude spectrum(a)、(b) 波形对比图 ；(c)、(d) 振幅谱对比图

3 瑞雷波频散曲线分析

通过对设计的七种随机介质模型正演数据利用相移法提取频散曲线，将均匀介质模型及自相关长度分别为α=1、β=1；α=100、β=1；α=1 000、β=1；α=5 000、β=1的频散曲线对比如图7所示。图8为均匀介质模型及自相关长度α=1、β=1；α=50、β=50；α=100、β=100的随机模型提取的频散曲线对比图。

图7 自相关长度α变化频散曲线对比图Fig.7 Comparison figure of frequency dispersion curve with change of autocorrelation length α(a) 震源主频率500 Hz；(b) 震源主频率1 000 Hz；(c) 震源主频率2 500 Hz

图8 自相关长度α、β同时变化频散曲线对比图Fig.8 Comparison figure of frequency dispersion curve with change of autocorrelation length α and β(a) 震源主频率500 Hz；(b) 震源主频率1 000 Hz；(c) 震源主频率2 500 Hz

从图7(a)、图7(b)及图8(a)、图8(b)可见，当震源主频为500 Hz、1000 Hz时，随机介质模型的频散曲线均处在均匀介质模型频散曲线附近上、下波动，波动范围最大值仅为1.7%。在图7 (c)中的2 000 Hz～4 000 Hz段，随机介质模型的频散曲线相对于均匀介质模型频散曲线上、下波动范围不超过1.3%，而在4 000 Hz～10 000Hz段，自相关长度α=5 000、β=1的随机介质模型的频散曲线迅速偏离均匀介质模型的频散曲线，偏差值可达7.2%，其余自相关长度下的频散曲线保留原趋势，偏离均匀介质模型频散曲线均不超过1.4%。在图8(c)中的3 000 Hz～5 000 Hz段，波动范围不超过1.6%，而在5 000 Hz～9 000 Hz段，自相关长度α=100、β=100时，其偏差值不超过2%，其余情况下不超过0.6%。从以上分析可知：震源主频较低即波长较大时，随机异常体对瑞雷波频散曲线影响较小；而震源主频较高即波长较小时，随机异常体对瑞雷波频散曲线影响较大。

将不同震源主频下各随机介质模型以及均匀介质模型频散曲线速度值的最大偏差值进行汇总(表1)。从表1中可以看出，随机介质模型中随机异常体会引起频散曲线速度值的变化：①当自相关长度α=1、β=1的随机介质模型中的单尺度随机异常体尺度较小时，所引起的速度偏差值不超过0.8%；②当自相关长度α=50、β=50及α=100、β=100的随机介质模型中单尺度随机异常体尺度增大时，所引起的速度偏差值也不超过2%，对于此类有单尺度异常体组成的地层，随机异常体的尺度远小于波长时，所引起的频散曲线速度变化较小，可视其为均匀介质；③对于自相关长度α=1 000、β=1 000类似的随机介质模型，其随机异常体的尺度大于或相当于波长时，与均匀介质频散曲线的速度值偏差值均不小于5.9%，就不能视其为均匀介质；④对于自相关长度α=5 000、β=1所对应的随机介质模型，已相当于介质模型中的细密薄层，其所引起的速度偏差值可高达7%以上，对于此种情况，在利用频散曲线进行分析时，必须考虑介质非均匀性的影响。

表1 随机介质模型与均匀介质的频散曲线速度的最大偏差值百分比(%)

Tab.1 The maximum percentage deviation of frequency dispersion curve in random medium and homogeneous medium (%)

震源主频/Hz模型α=1β=1α=50β=50α=100β=100α=1000β=1000α=100β=1α=1000β=1α=5000β=15000.81.61.66.71.20.91.010000.61.70.95.91.21.10.725000.60.81.58.01.40.97.2

4 结论

运用高斯型自相关函数构建了七种随机介质模型，利用高精度交错网格有限差分法对构建的随机介质模型进行正演模拟，通过分析不同主频及不同自相关长度的随机介质模型的波场特征和频散曲线特征，得到以下结论：

1)随机介质模型中瑞雷波能量较之均匀介质中减弱，其到达时间也发生变化,但其波形与均匀介质中基本一致；不均匀体所引起的散射波出现在面波之后，其能量小于面波的能量。

2)在实际的瑞雷波勘探中，对于由单尺度异常体组成的随机介质地层，当不均匀体的尺度小于波长时，对频散曲线速度值的影响较小，可视其为均匀介质；当不均匀体的尺度超过波长或与之相当时，对频散曲线的影响较大，就不能视其为均匀介质；由细密薄层构成的地层对频散曲线的影响较大，必须考虑介质非均匀性的影响。

[1]蒋婵娟.瑞雷面波资料处理方法研究[D].长沙：中南大学，2009.JIANG C J.Study on methods of Rayleigh surface wave data processing[D].Changsha:Central South University,2009.(In Chinese)

[2]陈艳艳.瑞雷波频散曲线提取及快速反演分析应用研究[D].哈尔滨：哈尔滨工业大学，2010.CHEN Y Y.Application and research on dispersion curves and the rapid inversion method of rayleigh wave[D].Harbin：Harbin Institute of Technology,2010.(In Chinese)

[3]IKELLE L T,YUNG S K,DAUBE F.2-D random media with ellipsoidal autocorrelation functions[J].Geophysics,1993,58(9):1359-1372.

[4]TOBIAS M M,SERGE A S.Green's function construction for 2D and 3D elastic random media[C].SEG Technical Program Expanded Abstracts,1999:1797-1800.

[5]奚先,姚姚.随机介质模型的模拟与混合型随机介质[J].地球科学:中国地质大学学报,2002,27(1):67-71.XI X,YAO Y.Simulations of random medium model and intermixed random medium[J].Earth Science-Journal of China University of Geoscience,2002,27(1):67-71.(In Chinese)

[6]姚姚,奚先.区域多尺度随机介质模型及其波场分析[J].石油物探,2004,43(1):1-7.YAO Y,XI X.Regionalize multi-scale random medium model and its seismic wavefield analysis[J].GPP，2004,43(1):1-7.(In Chinese)

[7]姚姚,奚先.随机介质模型正演模拟及其地震波场分析[J].石油物探,2002,41(1):31-36.YAO Y,XI X.Modeling in random medium and its seismic wavefield analysis[J].GPP，2002,41(1):31-36.(In Chinese)

[8]奚先,姚姚.二维弹性随机介质中的波场特征[J].地球物理学进展,2005,20(1):147-154.YAO Y,XI X.Wave field characters of 2-D elastic random medium[J].Progress in Geophysics,2005,20(1):147-154.(In Chinese)

[9]奚先,姚姚.二维粘弹性随机介质中的波场特征分析[J].地球物理学进展,2004,19(3):608-615.YAO Y,XI X.The analysisi of the wave field characteristics in 2-D viscoelastics random medium[J].Progress in Geophysics,2004,19(3):608-615.(In Chinese)

[10]王慧琴,刘正东,王冰.二维随机介质中的能量分布和频谱特性[J].物理学报,2008,57(9):5550-5557.WANG H Q,LIU Z D,WANG B.Energy distribution and spectral properties of two-dimensional random medium [J].Acta Physics Sinica,2008,57(9):5550-5557.(In Chinese)

[11]朱生旺,魏修成,曲寿利,等.用随机介质模型方法描述孔洞型油气储层[J].地质学报,2008,82(3):420-427.ZHU S W,WEI X C,QU S L,et al.Description of the carbonate Karst reservoir with random media model[J].Acta Geologica Sinca,2008,82(3):420-427.(In Chinese)

[12]肖云飞,殷厚成,孙成禹,等.基于随机介质模型的近地表波场模拟及分析[J].石油物探,2011,50(4):336-344.XIAO Y F,YIN H C,SUN C Y,et al.The near-surface wave field simulation and analysis of based on Random medium model [J].Geophysical Prospecting for Petroleum,2011,50 (4):336-344.(In Chinese)

[13]张大洲,熊章强,顾汉明.高精度瑞雷波有限差分数值模拟及波场分析[J].地球物理学进展,2009,24(4):1313-1319.ZHANG D Z,XIONG Z Q,GU H M.Namerical modeling of Rayleigh wave using high-accuracy finite-difference method and wave field analysis[J].Progress in Geophys,2009,24(4):1313-1319.(In Chinese)

The forward modeling of Rayleigh wave and analysis of wave field characteristics based on random medium model

ZHAO Hong-xina,XIONG Zhang-qianga,b,ZHANG Da-zhoua,b

(a.Central South University School of Geosciences and Info-Physics,Changsha 410083,b.Central South University Key Laboratory of Metallogenic Prediction of Nonferrous Metals,Ministry of Education,Changsha 410083,China)

To study the effect of Rayleigh wave field characteristic in heterogeneity medium,high accuracy staggered grid method has been applied into random medium models with different autocorrelation length at a different main frequency source.Basis on this,we have got dispersion curve by the phase shift method and contrast snapshots,single-channel recording and dispersion curve.The results shows that the Rayleigh wave energy of random medium is less than that in a homogeneous medium,and the arrival time in random mediums changes caused by irregularities.The random medium whose size of irregularities greater than or comparable to the wave length and the stratum medium constituted by a fine thin layer influences more on the dispersion curve,we can't see them as homogeneous mediums for Rayleigh wave exploration in this case.

random medium; Rayleigh wave; dispersion curve; wave field characteristics

2015-10-09 改回日期：2016-02-23

国家自然科学基金(41274123)；博士点基金(20130162110066)

赵宏欣(1989-)，男，硕士，主要从事瑞雷波正研研究，E-mail：dazhou2005@163.com。

1001-1749(2016)06-0780-08

P 631.4