基于样条插值与曲波变换压缩感知的井下微地震监测数据重建

常 凯，张海江,b*,林 叶,b

(中国科学技术大学 a.地球与空间科学学院万泰微地震实验室，b.地震与地球内部物理实验室，合肥 230026)

基于样条插值与曲波变换压缩感知的井下微地震监测数据重建

常 凯a，张海江a,b*,林 叶a,b

(中国科学技术大学 a.地球与空间科学学院万泰微地震实验室，b.地震与地球内部物理实验室，合肥 230026)

对于非常规油气开发水力压裂井下微地震监测，由于井中布设的检波器数量有限而导致空间采样不够，致使在进行偏移成像时产生空间假频。为消除假频现象，需要对空间欠采样的数据进行内插。目前基于曲波变换(Curvelet)稀疏约束的地震道插值方法(即压缩感知)已经逐渐被广泛应用,但是对于井下微地震监测数据，由于检波器数量过少，其在时间上的采样点数要远远大于检波器数。在这种情况下，曲波基函数在一定尺度下所能取到的方向信息是有限的，致使其基函数各向异性特征不能很好地发挥，因此插值效果不好。为解决该问题，我们提出了结合样条插值的基于曲波变换稀疏约束地震道插值方法。对于井下微地震监测数据，首先利用样条插值方法对每道数据的特定震相到达时间进行插值，在达到曲波基函数可以取到的方向后(如水平方向)，此时曲波基函数可以更稀疏地表示微地震数据体，然后再进行基于曲波变换稀疏约束的道间插值，并进行方向滤波，即可以达到较好的插值效果。我们基于一个井下微地震监测合成数据进行了测试，与数据加密前的地震偏移成像结果对比，内插之后数据偏移成像中的假频得到了压制。

井下微地震监测； 样条插值； 曲波变换； 压缩感知； 数据重建

0 引言

对于非常规油气开发来说，例如页岩气和致密砂岩气的开采，由于储层渗透率低，必须采用水力压裂技术使地层产生裂缝以提供油气运移的通道。水力压裂井下微地震监测，是一种有效的刻画目标储层裂缝分布的手段。井下微地震监测指的是把一串检波器放在靠近压裂井的监测井中，接收裂缝发育过程产生的微地震信号并对微地震事件进行定位或者对界面偏移成像。但是由于监测成本和技术等因素限制，井下微地震监测通常只布置十几个检波器[1]。在利用井下检波器接收到的微地震波形进行偏移成像时，会由于道间距过大而出现空间假频现象[2]。为解决此类问题，微地震数据道间插值成为抗空间假频非常必要的一种手段[3]。

地震道集经过数学变换后可以用较少的基函数系数来表示[4]。Donoho等[5]提出了压缩感知技术，在理论上解决了在数据不满足Nyquist采样定理的情况时，具有稀疏性质数据如何重建的问题。在此理论框架下，多种基函数被应用到地震数据恢复中，常用的有傅里叶基函数，小波基函数和曲波(Curvelet)基函数等[6-8]。其中曲波基函数在稀疏表示地震道集上表现出了相当好的各向异性，局部性和多尺度特性。

Herrmann等[9-10]在曲波框架下基于压缩感知原理,对地震数据重建问题进行了深入的研究，取得了很好的效果。在国内，刘国昌等[11]将凸集投影(POCS)方法引入到基于曲波变换L1范数约束的地震道插值问题；张华等[12]采用了基于jilter采样的曲波变换对三维地震数据进行了重建;冯飞等[13]将三维曲波变换和焦点变换结合起来，对三维地震数据进行插值和去噪，取得了良好的效果。然而，当已知地震道数很少，同时又有较长的时间采样点数时(例如井下微地震监测数据)，若直接采用基于曲波变换稀疏约束的插值方法，由于曲波在具体尺度下的方向数是有限的，当同相轴不能符合其基函数的方向时，插值效果并不理想。

针对上述问题，笔者提出了一种样条插值与基于曲波变换稀疏约束反演相结合的方法对井下微地震监测数据进行加密。这里首先分析了压缩感知的基本原理并简要说明曲波变换的方向性和多尺度特性；然后提出结合样条插值和基于曲波变换稀疏约束数据重建的混合插值方法；最后基于一个井下微地震监测合成数据，比较了插值前后逆时偏移成像结果。

1 基于压缩感知数据重建基本原理

地震数据插值可以看成由欠采样数据到全部数据的一个数据重建反问题[14]。

d=M m

(1)

其中:d为观测到的数据;M为采样矩阵;m为想要恢复的全部地震数据,它可以通过数学变换W来进行稀疏表示，如式(2)所示：

x=Wm

(2)

通过对x的逆变换可以恢复m。如果数学变换W是一个正交变换，其逆变换与转置等价：

m=WTx

(3)

因此，地震数据插值问题可以进一步转化为稀疏约束优化问题，即得到的解一方面要拟合观测数据，另外要保持其稀疏性，对应的优化问题的目标函数，如式(4)所示。

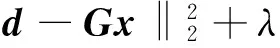
(4)

其中:G=MWT;λ为正则化参数;‖·‖0表示x中非零元素个数，即稀疏性。因为0范数约束方程求解时不可导，且为NP-hard问题，所以通常利用1范数替代[15]。最后得到最优化问题的目标函数为：

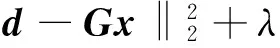
(5)

这里采用SPG_L1方法求解此泛函，其基本原理是将基追踪(Basis Pursuit)问题转化为一系列的最小绝对收缩和选择(Least Absolute Shrinkage and Selection)问题进而求解[16]。因为曲波变换具有良好的多尺度特性和一定的方向特性，所以地震数据插值问题中的数学变换W可选为曲波变换。

在离散曲波变换中，由于其基函数的方向特性，空间不同方向的分量可以在曲波域中离散表示(如图1)。对于二维函数f(n1,n2),0≤n1,n2≤n，其在笛卡尔坐标系下的曲波系数可以表示为：

(6)

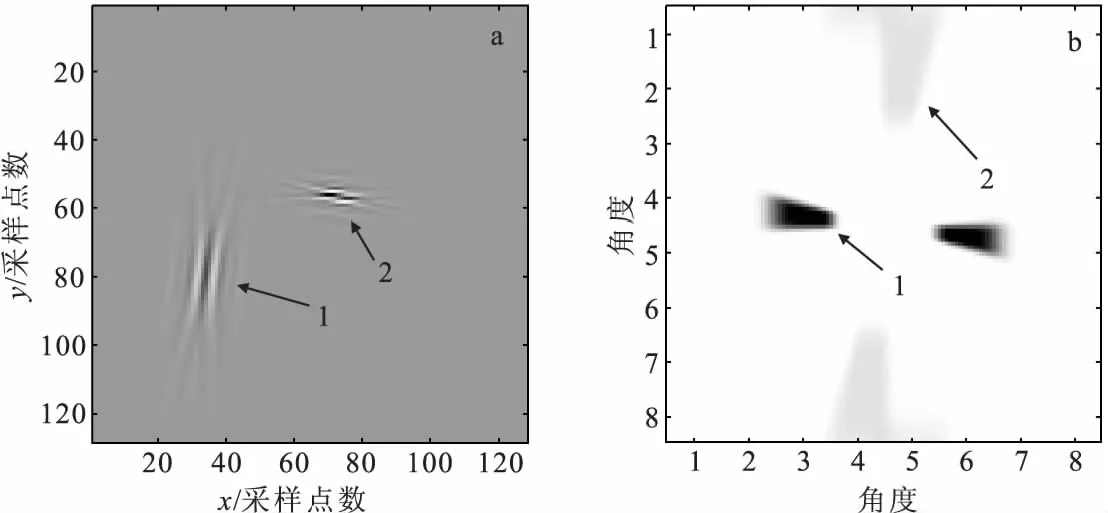
图1 数据在空间域与曲波域的表示Fig.1 Data representation in both space domain and curvelet domain(a)空间域数据；(b)对应于空间域数据的曲波系数

图1(a)为空间域中两个“同相轴”，在曲波域中可以表示为不同位置，不同尺度，不同角度稀疏的曲波系数(图1(b))。由于一般情况下相邻地震道“同相轴”不会在近垂直方向，因此可以通过对曲波系数按照方向特征滤波，滤掉在空间域中近垂直分量，达到提高插值效果的目的。

2 联合样条函数基于曲波变换的稀疏约束插值

基于压缩感知技术插值的前提条件,是波形可以在变换域中稀疏表示。然而对于微震数据，由于井下检波器数过少，致使曲波基函数无法直接稀疏表示全部微震数据。由于以上条件限制，我们将样条插值与基于曲波变换的稀疏约束插值相结合。当样条方向与曲波基函数所能稀疏表达的方向一致时，此时的曲波变换能够使数据较好地稀疏表示，进而利用压缩感知技术插值。其中三次样条插值以其兼顾低次插值稳定性和高次插值光滑性的优点,已在工程中得到广泛应用[18]。

对于空间欠采样的井下微地震监测数据，为压制微震成像时产生的空间假频，采取以下技术流程来实现微震数据特定震相的重构。

1)对于高信噪比的数据，利用相邻两道的波形相似性并基于整体的背景速度，在微震波形中找到相同的震相，此震相视需要而定。

2)利用样条插值拟合同相轴的形态，得到所有要插值的地震道上特定震相在时间轴上的位置。

3)基于样条插值得到的相同震相的位置，对每个地震道在时间轴上截取相同的时间，然后使相同震相在曲波基函数能够稀疏表达的方向上(水平方向)对齐。

4)对齐后的数据在曲波域中可以得到更稀疏的表示，满足稀疏约束条件，进而利用压缩感知技术进行插值并进行方向滤波。

5)将插值后的数据再返回到原来的位置上，最终实现微地震数据的特定震相的重构。

为了测试联合样条插值和曲波变换的数据重构效果，我们构建了一个井下微地震监测系统(图2(a))。理论模型的背景P波速度为4 200 m/s，裂缝作为一个低速异常位于(1 000 m,2 200 m)附近，速度为3 570 m/s。34级检波器(三角形)等间距地安装在x=445 m的监测井处，深度范围为975 m～1 965 m，空间间隔为30 m。在低速体和监测井之间(800 m,2 100 m)附近存在8个微地震事件(星形)。利用有限差分方法基于声波方程计算了8个微地震事件的地震波场。图2(b)显示了一个微地震事件被34个检波器接收到的地震合成波形。由图2(b)可以看出，直达波以及对应于低速裂缝区域的散射震相。逆时偏移成像方法用于微地震成像时，如果是对微震位置定位，那么只需要将直达波反传。因为后续散射波可认为由二次震源产生，在反传时会在强散射点处加强，有可能在定位时造成一定程度的干扰；如果不考虑定位，比如已知位置的射孔事件，而是对裂缝等低速结构成像，那么就类似于传统勘探手段中的逆时偏移方法。反传时若含有直达波，同样也会对最终成像结果产生干扰。对于实际数据来说(图2(c))，我们可以较容易地拾取直达波震相，然而对于后续散射波的同相轴较难拾取，故而利用实际数据成像时选择直达波后一段波形来进行加密。

图3为该技术应用在模型上的算例。由于只对低速区界面成像，图3(a)显示了只包含后续散射震相的34个地震道。我们对原始数据进行均匀抽稀，得到了12个地震道，空间间距为90 m(图3(b))，即稀疏度为66 %。首先拾取已有地震道相同震相最大振幅所对应的到时，并根据样条插值计算丢失地震道的到时，然后确定数据重构的时间窗(图3(c))，最后根据到时把时间窗向上移动进行展平(图3(d))。在这个基础上，对展平之后时间窗内的地震道根据公式(5)给出的曲波变换稀疏约束插值方法进行数据重构(图3(e))，接着根据到时再把时间窗移回原来的位置(图3(f))。为了比较，我们直接利用了基于曲波变换稀疏约束的内插方法进行数据重构(图3(g))。为验证该方法的普适性，用相同的技术路线测试了既包含直达波也包含后续散射波的欠采样数据插值(图3(h))，可以看出，直达波和散射波都具有较好的插值效果。

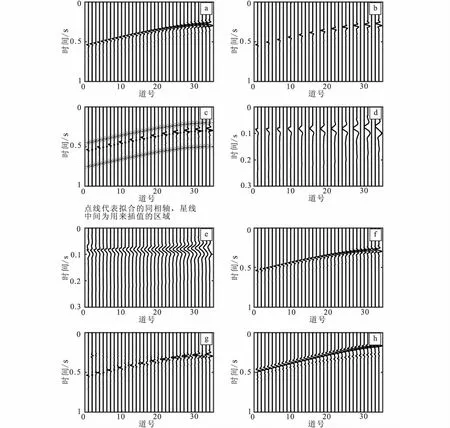
图3 联合样条插值与曲波变换稀疏约束数据重构方法对一个微地震事件合成道集的测试Fig.3 Test on synthetic waveforms from a microseismic event for joint spline and curvelet-based sparsity constrained interpolation method(a)原始34道合成数据；(b)均匀抽稀后的12道原始数据； (c)利用样条插值拟合散射震相的同相轴；(d)水平对齐后的数据；(e)对齐后应用曲波变换稀疏约束插值的数据；(f)最终插值结果；(g)直接利用曲波变换稀疏约束插值得到的数据；(h)包含了直达波和后续散射波的欠采样波形用该技术插值效果

在仅有12道数据的情况下联合样条插值重构的地震数据，地震相位连续，效果良好(图3(f))。与直接用曲波变换稀疏约束插值的结果相对比(图3(g))，联合方法的插值结果在相位连续性以及波形相似性更好。

为了进一步检验我们的方法对数据的恢复情况，计算了重构数据与正演合成数据的差值(图4)。由图4可以看出，联合样条插值的方法能够更精确地恢复振幅(图4(a)、图4(c))。我们进一步选取了其中差值最大的一道数据进行波形对比(图4(b)、图4(d))。可以看出联合了样条插值的基于曲波变换稀疏约束的数据重构方法能够很好地恢复相位、振幅。相比较而言，直接基于曲波变换的插值方法虽然也在一定程度上恢复了相位，但是存在一定程度的偏差，而且振幅恢复较差。

为定量说明重建后的数据和正演合成数据的差别，在这里把正演合成数据与重建数据的差值当作“噪声”，把正演数据作为“信号”，引入信噪比的概念来定量评价插值数据的恢复质量[8]：

(7)

其中:m0为正演合成的34道数据；m1为重建数据；SNR单位为dB。经计算直接用曲波变换插值重构的数据信噪比仅为-1.8 dB，而联合样条插值和曲波变换的插值方法重构的数据信噪比为14.8 dB。

3 井下微地震合成数据加密前后成像效果对比

为检验该方法加密数据压制空间假频的有效性，将其应用于图2所示井下微地震合成数据的偏移成像中。利用8个微地震事件的全部34道微震数据并基于声波方程进行了逆时偏移成像(图5(a))。其基本原理为从震源发出的正传波场与井下检波器所计算的逆推波场，在成像点处对传播方向不同的波场应用互相关成像条件成像[19-20]。由图5(a)可以看出，裂缝区域能够很好地被刻画出来。如果利用抽稀后的12道微震数据进行成像，虽然裂缝区域能够较好地成像，但是在监测井附近存在较强的空间假频现象(图5(b))，这主要是由于微震波场空间采样不够所导致的。如果不联合样条插值，直接利用曲波变换进行数据重构得到34道微震数据，然后进行偏移成像(图5(c))。由图5(c)可以看出，虽然地震道进行了加密，但是由于插值效果较差，成像的结果依然显示出与图5(b)类似的空间假频现象。与之不同的是，结合样条插值基于曲波变换的数据重构方法能够很好地恢复数据，而且成像结果中也不存在由于空间采样不足而产生的空间假频现象(图5(d))。

通过对比图5(a)～图5(d)，我们还可以发现，加密后的数据与全部数据相比，在裂缝远离监测井的界面成像效果稍有不足。加密后的数据和原始稀疏的数据相比，除了能够更好地压制假频之外，对裂缝的成像效果并没有太多形态上的差别。这说明基于样条插值和曲波变换压缩感知方法加密数据，并没有带来新的有效信息。

4 结论与讨论

笔者提出了联合样条插值与曲波变换稀疏约束的数据重构方法，并用于压制微地震偏移时由于空间采样不足而产生的假频。基于井下微地震监测合成数据测试，取得以下几点认识：

1) 基于数学变换稀疏约束插值的前提，是地震道集图像可以在变换域稀疏表示。对于曲波变换来说，只有当同相轴所表示的方向与其所对应的尺度下基函数所能刻画的方向一致时，才可以稀疏表示全部地震道集，从而得到较好的插值效果。

2)联合样条插值与曲波变换稀疏约束的插值方法，可以针对在较少地震道的情况下，通过同相轴追踪较好地进行地震数据重建。避免了当已知地震道较少时，曲波基函数对整个地震道难以进行稀疏表示的问题。

3)合成测试结果表明，针对空间采样不足，用联合方法加密微地震监测数据可以压制偏移成像时出现的假频现象，而并不带来新的有效信息。

[1]张永华,陈祥,杨道庆,等.微地震监测技术在水平井压裂中的应用[J].物探与化探,2013,37(6):1080-1084.ZHANG Y H,CHEN X，YANG D Q，et al.Application of microseismic monitoring technology in horizontal well fracturing [J].Geophysical and Geochemical Exploration,2013,37(6):1080-1084.(In Chinese)

[2]刘财,李鹏,刘洋,等.基于seislet变换的反假频迭代数据插值方法[J].地球物理学报,2013 (5):1619-1627.LIU C,LI P,LIU Y,et al.Iterative data interpolation beyond aliasing using seislet transform.[J].Chinese Journal Geophysics,2013 (5):1619-1627.(In Chinese)

[3]林叶，张海江.水力压裂裂缝微地震逆时偏移成像[C].2015年中国地球科学联合学术年会——专题52:微地震监测与反演，2015:2273-2274.LIN Y,ZHANG H J.Reverse time migration imaging of microseismic data in hydraulic fracturing [C].Annual meeting of the Chinese Academy of Earth Science,2015.Special 52:microseismic monitoring and inversion，2015:2273-2274.(In Chinese)

[4]刘洋,王典,刘财.数学变换方法在地震勘探中的应用[J].吉林大学学报:地球科学版,2005,35(专辑) :1-8.LIU Y,WANG D,LIU C.The application of mathematical transform in seismic exploration [J].Journal of Jilin University:Earth Science Edition,2005,35 (Spec):1-8.(In Chinese)

[5]DONOHO D L.Compressed sensing[J].Information Theory,IEEE Transactions on,2006,52(4):1289-1306.

[6]LUO T,LIU C,YANGX T,et al.Seismic data reconstruction based on iterative linear expansion of thresholds[J].Global Geology，2015,18(2) :127-133.

[7]崔兴福,刘东奇,张关泉.小波变换实现地震道内插[J].石油地球物理勘探,2003,38(B11):93-97.CUI X F,LIU D Q,ZHANG G Q.Wavelet transform to achieve seismic interpolation [J].Oil Geophysical Prospecting,2003,38(B11):93-97.(In Chinese)

[8]冯飞,王德利,张亚红,等.结合曲波变换的焦点变换在地震数据去噪和插值中的应用[J].物探与化探,2013,37(3):480-487.FENG F,WANG D L,ZHANG Y H,et al.The application of focal transform in combination with curvelet transform to seismic data denoising and interpolation[J].Geophysical and Geochemical Exploration,2013,37(3):480-487.(In Chinese)

[9]NAGHIZADEH M,SACCHI M D.Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data[J].Geophysics,2010,75(6):WB189-WB202.

[10]HERRMANN F J,HENNENFENT G.Non-parametric seismic data recovery with curveletframes[J].Geophysical Journal International,2008,173(1):233-248.

[11]刘国昌,陈小宏,郭志峰,等.基于Curvelet变换的缺失地震数据插值方法[J].石油地球物理勘探,2011,46(2):237-246.LIU G C,CHEN X H,GUO Z F,et al.Missing seismic data rebuilding by interpolation based on Curvelet transform [J].Oil Geophysical Prospecting,2011,46(2):237-246.(In Chinese)

[12]张华,陈小宏.基于 jitter 采样和曲波变换的三维地震数据重建[J].地球物理学报,2013 (5):1637-1649.ZHANG H,CHEN X H.Seismic data reconstruction based on jittered sampling and curvelet transform [J].Chinese Journal Geophysics,2013 (5):1637-1649.(In Chinese)

[13]冯飞.结合稀疏变换的稀疏约束反演一次波估计研究[D].长春：吉林大学,2014.FENG F.A study of estimation of primaries by sparse inversion in combination with sparse transformation [D].Changchun:Jilin University,2014.(In Chinese)

[14]SHANG X F.Inverse scattering:theory and application to the imaging of the Earth's seismic discontinuities[D].Boston:Massachusetts Institute of Technology,2014.

[15]ASTER R C,BORCHERS B,THURBER C H.Parameter estimation and inverse problems[M].Waltham:Academic Press,2011.

[16]谢志鹏.压缩感知的稀疏重构算法研究[D].南京：南京航空航天大学,2012.XIE Z P.Research on sparse reconstruction algorithms in compressive sensing [D].Nanjing:Nanjing University of Aeronautics and Astronautics,2012.(In Chinese)

[17]CANDES E,DEMANET L,DONOHO D,et al.Fast discrete curvelet transforms[J].Multiscale Modeling & Simulation,2006,5(3):861-899.

[18]周强,曹琳昱,曹中林,等.样条曲线拟合初至波剩余静校正方法[J].地球物理学进展,2015 (3):1329-1332.ZHOU Q,CAO L Y,CAO ZH L,et al.A method of residual static corrections based on fitting first break using spline function [J].Progress in Geophysics,2015(3):1329-1332.

[19]林叶.VSP 逆时偏移角道集域成像方法与应用[D].北京：中国地质大学 ,2014.LIN Y.VSP reverse time migration angle gather domain imaging method and application [D].Beijing:China University of geosciences,2014.(In Chinese)

[20]LIU F,ZHANG G,MORTON S,et al.An effective imaging condition for reverse-time migration using wavefield decomposition[J].Geophysics,2011,76:s29-s39.

Downhole microseismic monitoring data reconstruction based on spline interpolation and curvelet-based compressive sensing

CHANG Kaia，ZHANG Hai-jianga,b*，LIN Yea,b

(University Science and Technology of China a.Wantai Microseismic Lab of School of Earth and Space Sciences,b.Laboratory of Seismology and Physics of Earth's Interior,Hefei 230026,China)

For downhole microseismic monitoring of hydraulic fracturing of unconventional oil/gas reservoirs,the number of borehole receivers is limited and as a result the spatial sampling of seismic wavefield is sparse,which can lead to artifacts in the seismic migration image for downhole microseismic migration.To mitigate this spatial aliasing issue,spatial interpolation is needed.Currently,compressive sensing using the curvelet-based sparsity constraint has been gradually widely used for seismic trace interpolation.However,for the case of downhole microseismic monitoring,because the temporal sampling is much denser than the spatial sampling,the directional information obtained for curvelet bases at certain scales is limited,making it difficult to take full advantage of anisotropic features of curvelet bases.As a result,the result of seismic trace interpolation is poor.To solve this issue,we propose a hybrid method that combines spline interpolation and curvelet-based compressive sensing.First,spline interpolation method is used to calculate the reflection of interpolated traces using those of existing traces.Then the traces are shifted to a certain direction that could well be represented by the curvelet basis,such as the horizontal direction.After shifting the traces,the seismic gather is sparse in the curvelet domain and thus the curvelet-based spartisty constrained interpolation can then be used to more accurately reconstruct more traces in the space domain.We tested the hybrid method on a synthetic downhole microseismic dataset.It shows that the artifacts on seismic migration image using interpolated microseismic data are greatly reduced compare to the migration image from the original sparse data.

downhole microseismic monitoring; spline interpolation; curvelet transform; compressive sensing; data reconstruction

2015-11-13 改回日期：2015-12-24

国家自然科学基金项目(41274055)

常凯(1990-)，男，硕士，主要从事被动源地震成像，稀疏约束反演研究,E-mail：chao_13@mails.jlu.edu.cn。

*通信作者：张海江(1973-)，男，教授，主要从事不同尺度下地震成像算法研究和应用，E-mail：zhang11@ustc.edu.cn。

1001-1749(2016)06-0788-08

P 631.4