基于Copula函数的水文干旱联合概率分布研究
2017-01-11宋松柏中国电力建设集团西北勘测设计研究院有限公司陕西西安70065西北农林科技大学水利与建筑工程学院陕西杨凌700
袁 超,宋松柏(.中国电力建设集团西北勘测设计研究院有限公司, 陕西 西安 70065;.西北农林科技大学 水利与建筑工程学院, 陕西 杨凌 700)
基于Copula函数的水文干旱联合概率分布研究
袁 超1,宋松柏2
(1.中国电力建设集团西北勘测设计研究院有限公司, 陕西 西安 710065;
2.西北农林科技大学 水利与建筑工程学院, 陕西 杨凌 712100)
双变量联合分布及重现期计算是水文干旱研究的重要内容。根据游程理论确定水文干旱事件,利用Copula函数建立干旱历时和烈度的联合分布,计算不同干旱事件的重现期。实例分析结果表明,联合分布可以考虑干旱历时与烈度不同组合情况,计算的联合重现期大于边际分布计算结果,泾河和北洛河最长历时干旱事件联合重现期为480 a和342 a。
游程理论;水文干旱;Copula函数;双变量分布;重现期
干旱定量化研究以游程理论最为有效,干旱历时和干旱烈度是定量化研究干旱的两个重要要素。对于干旱历时和干旱烈度单变量概率分布,研究表明指数分布和伽玛分布分别是干旱历时和干旱烈度最为常用的两种分布[1-4]。2006年,Shiau J T[5]通过Copula函数建立了由标准化降雨指标(SPI)定义的干旱历时和干旱烈度的联合概率分布,为干旱分析提供了一种新的途径。2010年,许月萍等[6]以皮尔逊III型和伽马函数为边际分布,应用Copula函数模拟干旱历时和干旱烈度之间的相依关系。2014年,刘和昌等[7]基于Copula函数推导了条件最可能组合的计算公式。虽然Copula函数在流域水文干旱特性研究中已有较多应用[8-14],但由于干旱发生机理时空变化的复杂性,干旱特征变量的联合分布特性及相应的重现期计算仍将是干旱研究的重要内容。本文选取泾河和北洛河径流资料,采用Copula函数建立联合分布,分析泾河和北洛河流域的水文干旱特性。
1 游程理论
对水文干旱进行分析,一般采用Yevjevich的游程理论[6]。根据游程理论,设R0为阈值,当R大于或等于R0时即发生干旱,游程长度为干旱历时L,游程总量为干旱烈度S,相邻干旱事件开始发生时间差为干旱间隔时间T,从图1可以看出干旱事件3个重要指标的定义[6,16]。
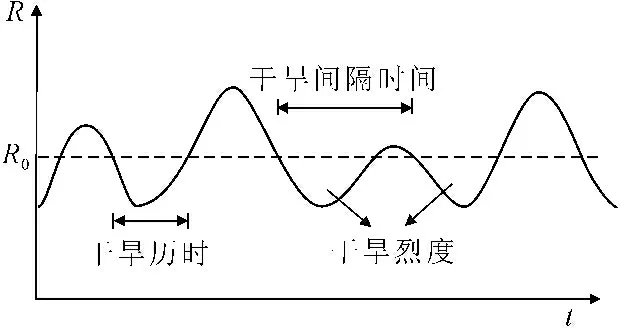
图1 干旱事件定义
2 边际分布函数
通常,干旱历时和烈度概率分布可以分别用指数函数与gamma函数描述,计算公式如下:
FL(l)=1-e-l/λ
(1)
(2)
式中:FL(l)、FS(s)分别为干旱历时l和烈度s的累积概率分布;λ、r、β为参数;Γ为gamma函数。
3 联合分布函数
Copula函数是定义域为[0,1]均匀分布的多维联合分布函数[5],定义如下:
假设两相依随机变量X和Y,Sklar定理表明如果FXY(x,y)是二维分布函数,Fx(x)和Fy(y)分别是其边际分布,则存在:
FXY(x,y)=C(FX(x),FY(y))
(3)
相反,如果任一单变量分布FX(x)和FY(y)及任一Copula C,那么FXY(x,y)是一二维分布函数,其边际分布分别为FX(x)和FY(y),且如果FX(x)和FY(y)是连续的,则C是唯一的。
假定FX(x)和FY(y)是连续的,fX(x)和fY(y)分别是其密度函数,那么联合概率密度函数为:
fXY(x,y)=c(FX(x)FY(y))fX(x)fY(y)
(4)
单参数Achimedean Copula函数族广泛应用于水文领域[7],本文介绍以下四种函数形式,见表1。

表1 单参数Achimedean Copula函数族计算公式
四种函数参数θ根据Kendall的秩相关系数τ估计,计算方法如下:
Gumbel-Hougaard函数:
τ=1-θ-1
(5)
Ali-Mikhail-Haq函数:
(6)
Frank函数:
(7)
Cook-Johnson函数:
(8)
4 条件概率计算
根据Copula函数的定义,干旱历时和烈度联合分布函数可表述为:
FL,S(l,s)=P(L≤l,S≤s)=C(FL(l),FS(s))
(9)
由此可知,两个要素的不同组合条件概率可分别按式(10)~式(11)计算。
P(L≥l,S≥s)=1-FL(l)-FS(s)+C(FL(l),FS(s))
(10)
P(L≥l∪S≥s)=1-C(FL(l),FS(s))
(11)
5 重现期计算
由于一场干旱可能持续多年或一年中发生多次干旱,常用于设计洪水的年最大序列频率分析已不在适用[16]。对于干旱历时和烈度联合重现期计算,2003年Shiau J T[17]给出如下计算公式:
(12)
(13)
式中:TLS为干旱事件(L≥l,S≥s)重现期;TLS为干旱事件(L≥l∪S≥s)重现期。
6 实例分析
根据泾河张家山站75 a和北洛河状头站70 a径流资料,截取水平取各月多年平均流量,确定的干旱事件经统计分析,状头站和张家山站干旱历时最长为25个月和19个月,而最大干旱烈度对应干旱历时为20个月和18个月,可见最长干旱历时对应的并不是最大干旱烈度,两者边际分布难以全面反映实际干旱程度。
采用极大似然法估算干旱历时和烈度边际分布的参数,并由公式(14)计算经验频率,检验指数分布和gamma分布对实测值的拟合程度,由计算结果可以看出,指数分布和gamma分布分别与实测值拟合较好,可以作为干旱历时和干旱烈度概率近似分布。
(14)
式中:P为概率;k为升序排列的位置值;N为样本容量。
由式(5)~式(8)计算状头站和张家山站四种Copula函数的θ值,见表2。采用公式(15)计算联合经验频率,检验四种Copula函数对实测组合值的拟合程度。结果表明,Cook-Johnson函数对实测干旱历时和干旱烈度组合值拟合效果较好,可用于建立干旱历时和烈度联合概率分布函数,见图2、图3。

表2 四种Copula函数的参数θ估计值
(15)
式中:P为概率;Nml为(xj,yj)满足xj
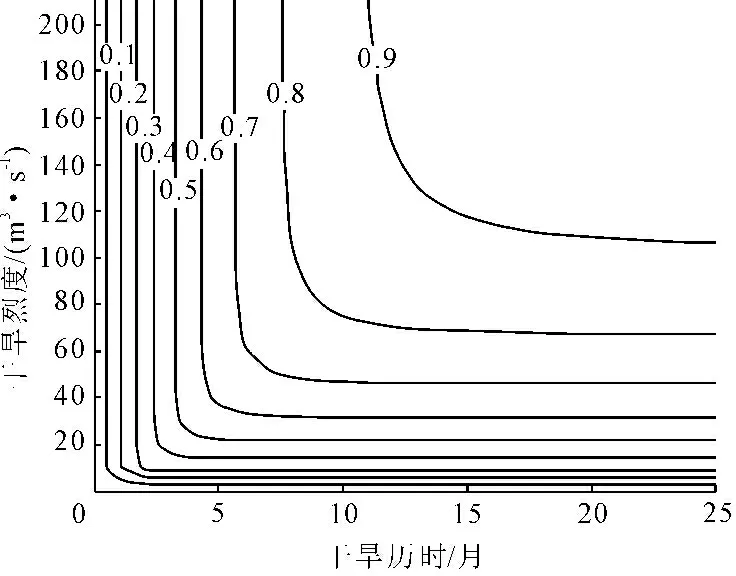

图2 状头站干旱历时与烈度联合概率等值线图
图3 张家山站干旱历时与烈度联合概率等值线图
若以历时作为干旱严重程度的衡量指标,状头站和张家山站最长干旱历时分别为25个月和19个月,由指数函数计算的重现期分别为138 a和43 a;而考虑与对应烈度的组合情况,则由式(12)计算联合重现期为480 a和342 a,可见联合重现期大于边际分布计算的重现期。状头站和张家山站干旱历时与烈度联合重现期等值线图见图4~图5。
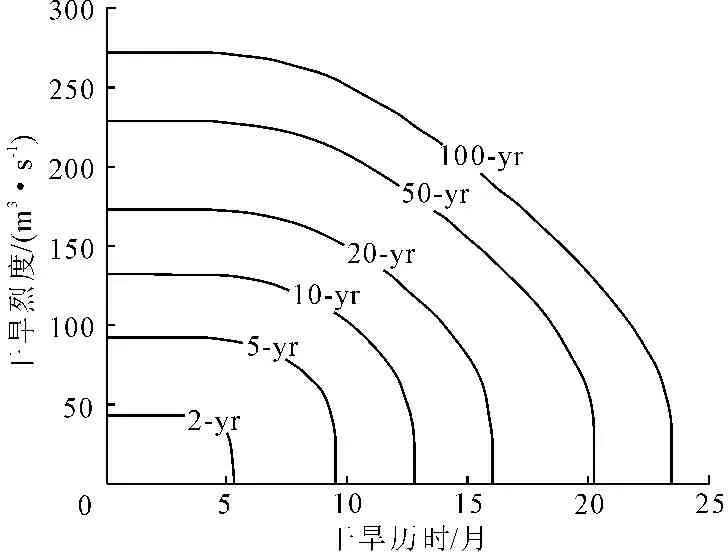
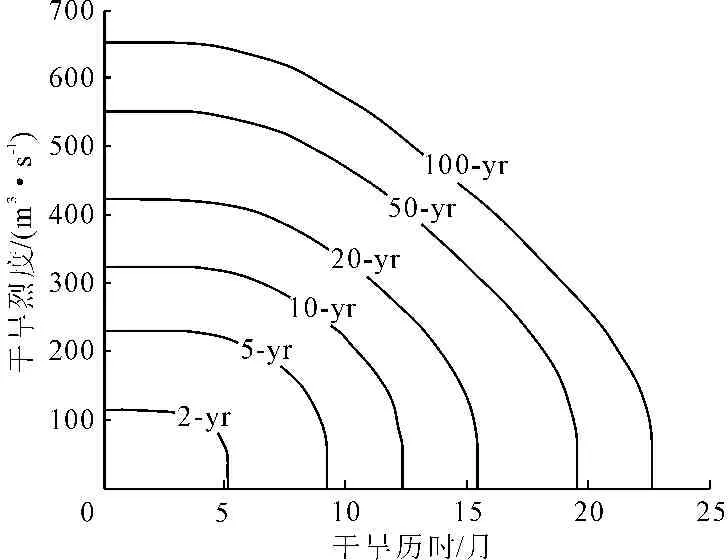
图4 状头站干旱历时和烈度联合重现期等值线图
图5 张家山站干旱历时和烈度联合重现期等值线图
7 结 论
(1) 利用Copula函数建立的联合分布考虑了干旱历时与烈度的不同组合情况,可以全面反映河流实际干旱情况。
(2) 干旱历时与烈度联合重现期大于其边际分布计算结果。
(3) 泾河张家山站最长干旱历时为25个月,与对应烈度的联合重现期为480 a;北洛河张家山站最长干旱历时为19个月,与对应烈度的联合重现期为342 a。
[1] 董前进,谢 平.水文干旱研究进展[J].水文,2014,34(4):1-5.
[2] 方红远,甘升伟,余莹莹,等.区域供水系统干旱历时特性综合分析[J].水科学进展,2007,18(1):95-101.
[3] 许 凯,徐翔宇,李爱花,等.基于概率统计方法的承德市农业旱灾风险评估[J].农业工程学报,2013,29(14):139-146.
[4] 田 佳.气象干旱研究进展[J].水利与建筑工程学报,2016,14(4):216-221.
[5] Shiau J T. Fitting Drought Duration and Severity with Two-Dimension Copulas[J]. Water Resource Management,2006,20(5):795-815.
[6] 徐月萍,张庆庆,楼章华,等.基于Copula方法的干旱历时和干旱烈度的联合概率分析[J].天津大学学报,2010,43(10):928-932.
[7] 刘和昌,梁忠民,姚 轶,等.基于Copula函数的水文变量条件组合分析[J].水力发电,2014,40(5):13-15.
[8] 李 计,李 毅,贺缠生.基于Copula函数的黑河流域干旱频率分析[J].西北农林科技大学学报(自然科学版),2013,41(1):213-220.
[9] 任 璐,赵雪花.基于Copula的汾河上游水文干旱频率分析[J].水力发电,2016,42(2):11-16.
[10] 刘 招,田 智,乔长录,等.基于Copula的关中河流水文丰枯遭遇特征分析[J].干旱地区农业研究,2013,31(4):245-248.
[11] 刘祖发,谭圣林,罗勇强,等.基于Copula函数的东江流域3大水库丰枯遭遇分析[J].琥珀科学,2015,27(2):361-370.
[12] 佘敦先,夏 军,杜 鸿,等.黄河流域极端干旱的时空演变特征及多变量统计模型研究[J].应用基础与工程科学学报,2012,20(S1):15-29.
[13] 陈再清,侯 威,左冬冬,等.基于修订Copula函数的中国干旱特征研究[J].干旱气象,2016,34(2):213-222.
[15] 彭高辉,宋 宝,马建琴,等.游程理论与二维Copula函数的耦合建模及应用[J].人民黄河,2013,35(9):8-11.
[16] 陆桂华,闫桂霞,吴志勇,等.基于Copula函数的区域干旱分析方法[J].水科学进展,2010,21(2):188-192.
[17] Shiau J T. Return period of bivariat distributed hydrological events[J]. Stochastic Environmental Research and Risk Assessment,2003,17(1):42-57.
The Bivariate Hydrologic Drought Distribution Based on Copula Function
YUAN Chao1, SONG Songbai2
(1.PowerChinaNorthwestEngineeringCorporationLimited,Xi’an,Shaanxi710065,China;2.CollegeofWaterResourceandArchitecturalEngineering,NorthwestA&FUniversity,Yangling,Shaanxi712100,China)
The bivariate distribution of drought and return period were an important issue in hydrological drought study. Hydrologic drought events were defined by the run theory, the bivariate distribution of drought duration and drought severity were developed by adopting Copula function in this paper, the return period formulations of drought event were proposed. The results showed that the bivariate distribution of drought took the various combinations of drought duration and drought severity into consideration. The return period of joint distribution was bigger than marginal distribution's. Return periods of Jing river and Beiluo river's drought with the longest duration were 480 years and 342 years.
runs theory; hydrologic drought; copula function; bivariate distribution; return period
10.3969/j.issn.1672-1144.2016.06.010
2016-04-24
国家自然科学基金项目(51179160,50879070,51079037);高等学校博士学科点专项科研基金项目(20110204110017)
袁 超(1983—),男,陕西岐山人,硕士,主要从事水文水资源研究。E-mail:121681618@qq.com
宋松柏(1965—),男,陕西永寿人,教授,主要从事水文水资源研究。E-mail:SSB6533@nwsuaf.edu.cn
P338.6
A
1672—1144(2016)06—0050—04
