电视塔的风致振动控制研究

程 怡(阳光学院 土木工程系， 福建 福州 350108)

电视塔的风致振动控制研究

程 怡
(阳光学院 土木工程系， 福建 福州 350108)

风灾是电视塔面临的主要自然灾害之一，主动控制方法可以有效地减小电视塔的风致振动。以一座空间钢管桁架电视塔为算例，首先基于ANSYS软件分析了该电视塔的动力特性，然后利用谐波合成法模拟了其随机风场，同时，还提出了一种形状记忆合金的主动控制方法，并编制了相应的线性二次型经典最优控制算法(LQR)，最后对比了采取控制措施前后电视塔的风致响应，结果表明形状记忆合金控制方法可以有效地减少电视塔的风致振动。

电视塔；动力特性；脉动风场；风致振动；主动控制方法

随着各国城市建设的发展，电视塔由原来只能作为发射电视讯号的单功能电视塔逐步向集通讯、展览、旅游、广告等文化活动和商业活动为一体的大型综合电视塔发展，所以电视塔通常也是一个城市的地标建筑物。电视塔一般采用自立式的塔式结构，是高耸结构中的一大组成部分。按结构材料划分，电视塔可分为三种：钢结构电视塔，钢筋混凝土电视塔和钢-混凝土组合电视塔。高度在300 m以上的电视塔主要是钢筋混凝土结构，而高度在300 m以下的电视塔主要采用钢结构。

但是由于钢结构截面小，高度大，刚度低，其抗风问题也尤为突出。由于电视塔这种高耸结构的高度大，结构抗弯刚度相对较柔，水平风荷载成为塔体的控制因素，在现有技术条件下钢结构塔高度受到限制[1]。近年来，随着高耸结构风致灾害的事故频繁发生，如何减少高耸结构在风荷载作用下的风致振动成为人们关注的焦点，而电视塔作为一种重要的现代高耸结构，因此开展电视塔的抗风性能研究及其风致振动的控制具有很重要的意义。

自20世纪50年代电视塔在世界各地开始大量兴建以后，国内外学者就针对电视塔的抗风性能及其振动控制展开了研究，主要集中在动力特性、抗风性能和控制措施三个方面：(1) 在动力特性方面，张志强等[2]和刘学利等[3]均对高阶振型对电视塔风振的影响进行了分析，结果表明高振型对钢结构电视塔的最大位移响应很小，一般考虑三阶或四阶即可满足计算精度要求，对于结构的加速度需要考虑高振型的影响，应该考虑八阶振型才能满足结构舒适度计算的要求。但他们的研究不足之处是都将电视塔模型简化为葫芦串式的二维模型，并未直接在原结构进行分析，所以得出的数据与真实数据存在一定的差别。张文福等[4]对大庆电视塔建立了有限元模型进行模态分析，得出对于大庆电视塔高振型的影响不可忽略，鞭梢效应显著，天线的振动在整个结构中占主导地位，原因是钢塔的质量和刚度沿高度方向不均匀。因此，需要进一步关注高阶振型对电视塔的风振影响。(2) 电视塔的抗风性能研究。张志强[5]对合肥电视塔风振及地震响应的振动控制研究分析表明合肥电视塔的地震响应与脉动风荷载作用下的风振响应相比，电视塔的响应以风振响应为主。唐振兴[6]对高耸通信塔抗风性能进行了分析，他选取沿高度不变的Davenport谱为风谱，用谐波叠加法来生成风速时程，得出了在只考虑顺风向风荷载的情况下根据规范计算较根据时程分析偏于保守。顾明等[7]对广州新电视塔进行了测力和测振的风洞试验研究，并采用随机振动CQC法对该塔进行了风致抖振响应及等效静力风荷载计算。罗书泉[8]对比分析了频域法和时域法对高耸电视塔结构的风振响应并相互验证了计算结果的可靠性，还分析了黏弹性阻尼器后对结构响应的控制效果。因此，为了研究电视塔的风致抖振响应，需要建立其地址区的风场，然后利用时程分析方法计算结构响应。(3) 结构振动控制的形式按照外加驱动能源的出力种类主要可分为被动控制、主动控制、混合控制和半主动控制。自20世纪50年代电视塔在世界各地开始大量兴建以后，国内外学者就针对电视塔结构的振动控制展开了研究[9-10]。国内电视塔振动控制的研究起步较晚，但是发展很快。王肇民[11]对高耸结构振动控制的理论、控制装置设计和参数优化进行了系统的研究，并针对电视塔天线的控制提出了悬挂弹簧阻尼器TSD。还有其他一些学者结合电视塔振动控制的工程实例在控制装置设计、控制效果实测及参数优化等方面做了许多工作[12-15]。然而，针对电视塔的主动控制的方法和应用相对还不成熟。

针对以上三方面的问题，本文以一座空间钢管桁架电视塔为算例，首先通过模态分析得到了该结构的自振频率和振型等，然后建立其地址区的风场，最后选取了一种形状记忆合金的主动控制方法，采用基于结构振动状态空间模型的LQR控制算法对电视塔的风振响应进行数值计算，对比得到结构在有无控制措施下位移、速度、加速度和内力响应，以验证其减振效果。

1 电视塔的有限元分析

选取一座总高度为168 m的电视塔，重量300 t，主体为钢管空间桁架结构，如图1所示。塔体分为天线段、塔楼、塔身3部分，标高92 m以下为5边形塔身，92 m～102 m为一碟形塔楼，116 m以上为4边形天线段，天线段的边长分别为2.5 m×2.5 m(标高116 m～135.5 m)、2.0 m×2.0 m(标高135.5 m～157.5 m)、0.7 m×0.7 m(标高157.5 m～168.5 m)。将该电视塔简化为15个质点的模型，塔柱、横杆和天线采用三维梁单元beam 189模拟，横杆和斜杆采用杆单元link 8来模拟，(电视塔结构阐述如表1所述)。其中塔柱和横杆都分别分成15层和10层来准确考虑各个层的截面特性，塔底截面节点采用固结形式处理，电视塔整体有限元模型一共有319个节点，329个单元，有限元模型见图2。选用Block Lanczos方法对该塔进行了模态分析，运用子空间迭代法求出结构的自振频率和模态振型，表2中列出了该塔的前6阶自振频率、周期和振动形式。

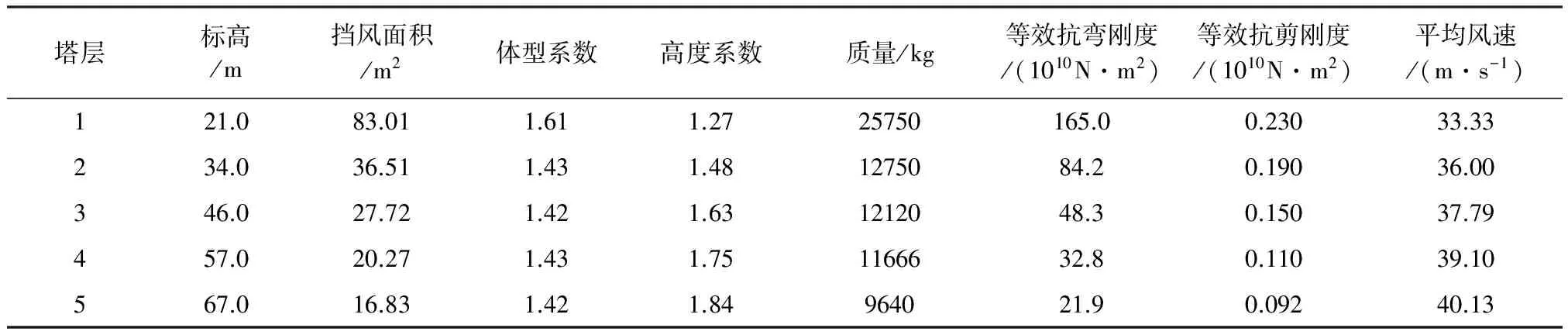
表1 电视塔的结构参数

由振型图3和自振频率可知，由于结构的对称性，出现多个频率相同的振型：该电视塔的第一阶和第二阶频率相同，均为0.414 Hz，但是天线的振动方向不同；第三阶和第四阶频率相同均为0.935 Hz，但是整体结构的振动方向不同；第五阶表现为整体扭转，第六阶表现为塔楼的振动。这种动力特性的特点表明前六阶振型对电视塔的结构响应存在一定的影响。

图1 电视塔实物图

图2 电视塔的有限元模型

2 随机风场的模拟

功率谱密度函数是平稳随机过程的主要数字特征，风速脉动分量的功率谱函数表示了紊流中各频率的成分所作贡献的大小。许多风工程专家对风功率谱进行了研究，得到了不同形式的风速谱表达式。其中用于结构设计的水平脉动风速谱主要有Davenport谱、Kaimal谱和Harris谱等；竖向脉动风速谱Panofsky-McCormick谱、Lumley-Panofsky谱等[14]。

模拟电视塔的风速时程时，由于电视塔高度上各点的风速不同，互谱密度函数需要考虑相位角，风谱密度矩阵(复数矩阵)有可能不正定。一般情况下脉动风的互谱密度函数为：

(1)

由于电视塔节点较多，需简化电视塔的模拟区域，本文沿高度变化将电视塔从下到上分为15段，各段中心点的实际高度见表3。用每段中心点的风速时程代表该段内各节点的风速时程。截止圆频率：12.56，频率等分数：1024，采样时距：0.25 s，相干系数：1，采样时间：600 s，粗糙高度：0.01 m。对于实际边界层风场中高度Zj处的风速UZj：

(2)

其中，Hg和α分别为梯度风高度和平均风速剖面的幂函数指数，对于该电视塔所处的B类地貌，HG=500 m和α=0.16。Ug为实际边界层风场中梯度风速。根据电视塔所在地气象部门提供的资料，当地50年重现期的基本风速为29.6 m/s。根据式(2)得到不同高度处的平均风速，如表3所示。

表3 电视塔架模拟点高度及各高度处平均风速

本文利用MATLAB软件，采用谐波合成法编写了模拟电视塔架结构多点的脉动风速程序，相关参数如下：(1) 假定该电视塔架所在地10 m高处的设计风速为30 m/s；(2) 时间步长0.25 s，采样时间600 s；(3) 选取能反映高度变化的Davenport谱为目标功率谱。经过模拟计算分别得到了各段中心点处的脉动风速时程曲线，如图4所示。

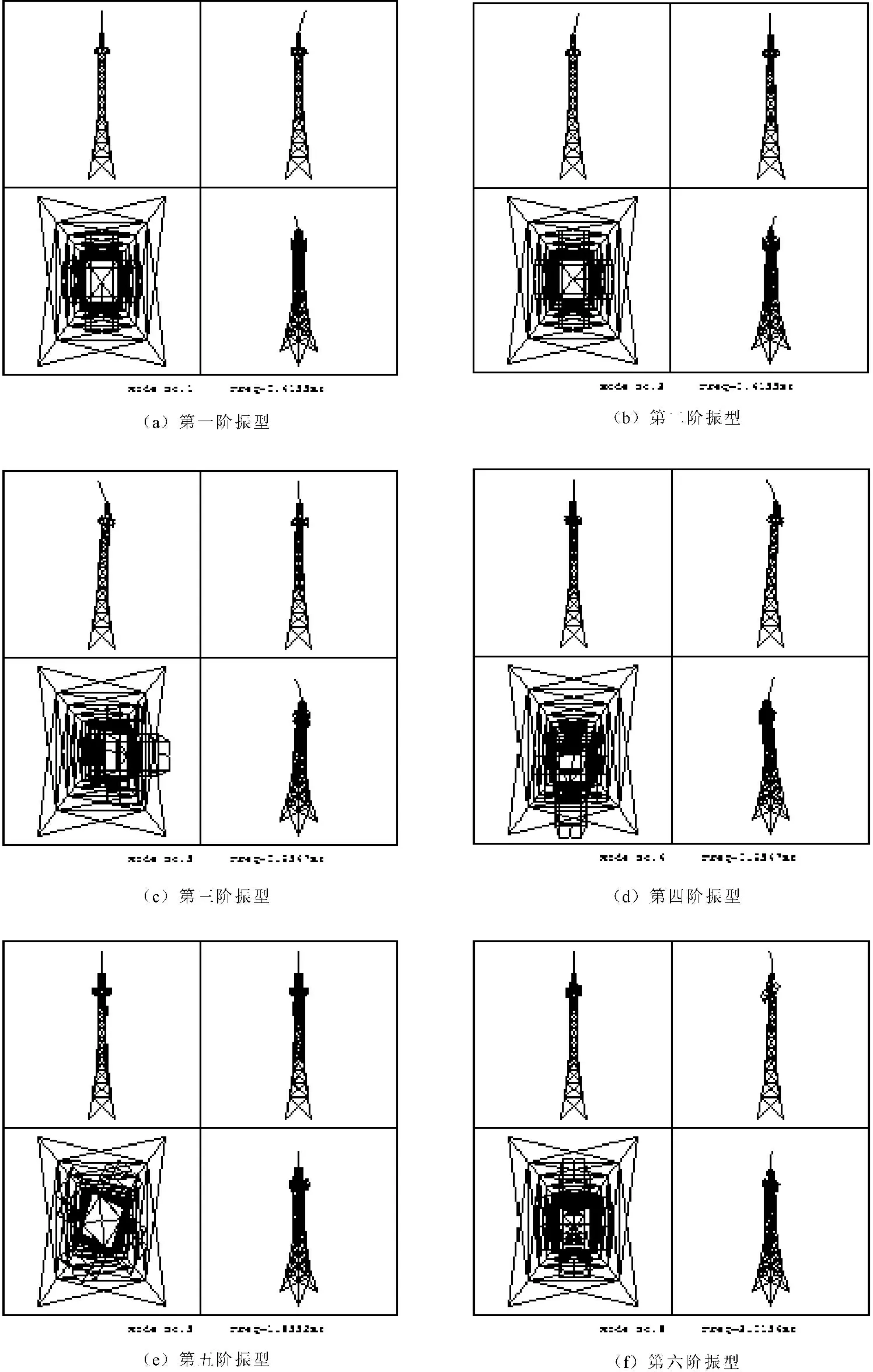
图3 前六阶的结构振型图

为了验证生成的风速时程符合要求，图5是风速时程的验证结果，由生成的脉动风功率谱和目标功率谱的符合程度以及生成的脉动风互相关函数和目标函数的符合程度可以看出此方法生成的风速时程满足要求。

由生成的风速时程可以根据下面的公式得出风荷载时程(F)：

(3)

(4)

P=P0+p

(5)

F=PAus

(6)

式中：P0、p、P分别代表平均风压、脉动风压、总风压；ρ代表空气密度；us代表体形系数。利用上面的计算方法，可得风荷载时程曲线，也即得到该电视塔的风场，如图6所示。

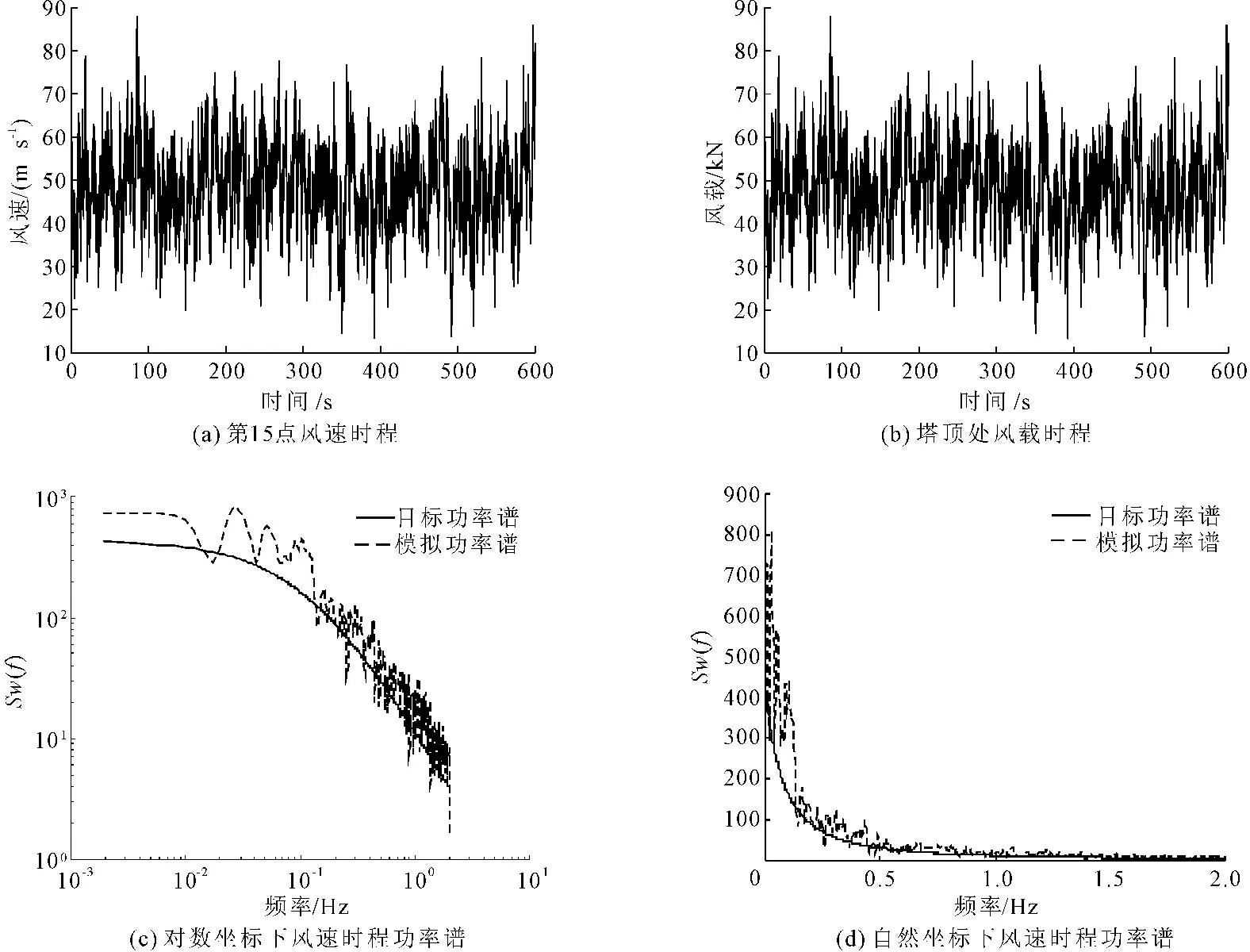
图4 各层点的风速时程曲线

图5 结构135.5 m处的风速和风荷载时程曲线以及两种功率谱的对比

图6 风荷载时程曲线

风荷载可以写成：

(7)

(8)

(9)

(10)

高耸结构考虑风与结构耦合的运动方程是一个复杂的非线性动力方程组，本文采用通用有限元程序ANSYS和数学软件MATLAB，针对结构的几何非线性，选用Newton-Raphson迭代法和Wilson-theta法等直接积分法进行数值求解。

3 形状记忆合金的主动控制方法和算法

选用形状记忆合金(SMA)作为控制器的智能材料，控制器由弹簧与SMA丝相组合，如图7所示。因为SMA具有相容性好、变形量大、加热后驱动力强、响应慢，兼具感应和驱动功能，比较适合制作成传感器/驱动器应用到土木工程中的结构振动控制中[15-16]。

图7 形状记忆合金控制方法

对于安装了形状记忆合金控制措施的电视塔整体结构，在风荷载和控制力作用下，结构的闭环控制运动方程可表示为：

(11)

式中：F(t)为外部荷载作用力向量；U(t)为结构上的控制力向量；Ds为风荷载位置矩阵； Bs为控制器的控制力作用位置矩阵。

为了寻求最优控制，使系统由任意给定的初始状态定义Z(t0)=Z0到终端状态Zf时，可设系统的二次型性能指标为：

(12)

式中：性能指标中的第一项是末值项，又称为终端代价，实际上是根据对控制的要求，在指定的时间点tf到来时，系统的终端状态Zf接近预期状态的程度。第二项中ZTQZ表示对结构振动响应的控制，UTRU表示对消耗控制能量的惩罚，Q和R是两个决定控制力和结构反应大小的相应维数的权矩阵。由式(12)表示的目标函数可以看出，权矩阵Q越大，结构的反应越小，控制力越大；R越小，控制力越大，结构的反应越小。

系统状态最优控制问题即为在无限时间[t0，∞]内，寻找最优控制U(t)，使系统从初始状态Z0转移到零状态附近，并使式(12)定义的性能泛函取极小值。因此，系统状态最优控制的问题在数学上描述为：

(13)

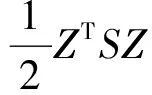
(14)

式(14)描述的控制问题是泛函条件极值问题，可采用变分法来求解。构造哈密尔顿函数H为：

(15)

式中：λT为拉格朗日乘子矢量。

使得哈密尔顿函数H取得极小值的必要条件为：

协态方程：

(16)

(17)

控制方程：

(18)

将式(15)代入式(17)，即可得到状态方程。

将式(15)代入式(18)，便得到：

(19)

由于R为正定矩阵，所以：

U(t)=-R-1BTλ(t)

(20)

由上式便可以确定最优控制，为了寻求最优反馈还需要把U(t)与状态向量Z(t)联系起来。由式(15)和式(16)，得到：

(21)

式(20)确定的U(t)是λ(t)的线性函数。为了使U(t)能由状态反馈实现，应该建立λ(t)与Z(t)之间的线性变换关系。设：

λ(t)=P(t)Z(t)

(22)

将式(22)代入式(20)，得：

U(t)=-R-1BTP(t)Z(t)

(23)

下面介绍求解P(t)的方法：

将式(23)代入式(21)，得式(21)等号的左端为：

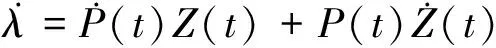
(24)

而式(21)等号的右端为：

-QZ(t)-ATλ(t)=-[Q+ATP(t)]Z(t)

(25)

将式(24)、式(25)代入式(21)，整理得：

(26)

按照控制的意义，当t→∞时系统状态充分接近零状态，但还不是零状态。这样，可以得到：

P(t)t→∞=0

(27)

上式即为式(26)求解P(t)时应满足的边界条件。

式(26)称为Riccati(里卡蒂)方程，P(t)称为Riccati矩阵函数，Riccati方程是一个非线性的矩阵微分方程。在求解式(25)Riccati方程时考虑到状态反馈Z(t)的任意性，式(26)可以简化为：

(28)

由上式求出P(t)后，则可得到最优控制力U(t)。

令：

G=R-1BTP(t)

(29)

则最后得到的最优控制的表达式为：

U(t)=-R-1BTP(t)Z(t)=-GZ(t)

(30)

式中：G为最优状态反馈增益矩阵。P(t)为Riccati方程的解。

由式(30)可以看出，最优控制U(t)取决于状态反馈Z(t)和反馈增益G。基于此，可以获得结构响应的最优的控制值。

4 控制效果对比分析

本文在该电视塔的每层质点上安装一个SMA控制器，但是根据表2中动力特性分析，天线段先于整体结构出现X、Z方向的振动，故需要在塔顶天线段的X、Z方向分别安装一个控制器。本文将ANSYS建立的模型调入MATLAB中，利用MABLAB建立了电视塔的风荷载和控制器的控制矩阵，如式(11)中右边荷载项，编写了SMA作动器的LQR控制算法，最后在MATLAB进行数值求解并输出计算结果。

结构模型是一个具有6n个自由度的电视塔结构(n为结构的节点数)，在电视塔中安装有16个SMA控制器。采用上述的基于结构振动状态空间模型的LQR控制算法，对有无采用SMA控制器的主动控制方法的电视塔风振响应进行了数值模拟计算。为了分析主动控制措施对高耸结构电视塔的风致响应影响，本文主要对比分析了是否考虑SMA控制器作用下该塔重要部位的位移响应、加速度响应和内力响应，响应最大值的结果见表4和表5。

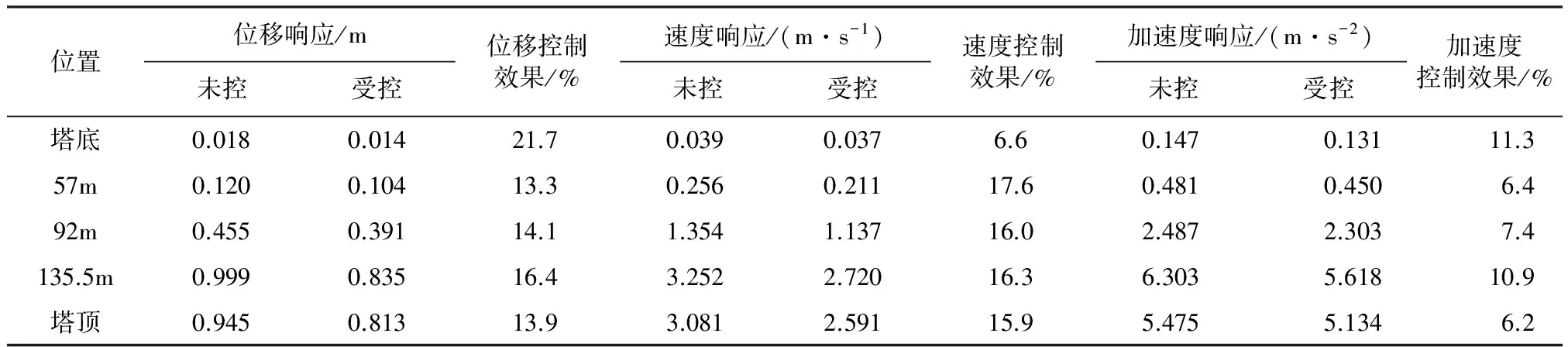
表4 该塔重要位置处的风致响应最大值对比

表4和表5表明，SMA控制器可以有效地减少电视塔的风致响应：对于位移响应， 塔底处的控制效果最大，达到了21.7%，塔顶的位移也从0.945 m减少到0.813 m；57 m处速度响应的控制效果最大，达到了17.65%，塔底处加速度响应的效果为11.3%；对于塔底的剪力和弯矩响应，主动控制效果分别为5.0%和48.4%，特别是弯矩的最大值从8690 kN/m减小为4 486.7 kN/m。

表5 该塔塔底内力响应对比

5 结 论

本文首先建立了一座高耸电视塔的有限元模型和风场，然后基于一种形状记忆合金主动控制方法编写了LQR控制算法程序，对比计算了该电视塔结构在有无该主动控制措施作用下结构的风振响应。主要的结论如下：

(1) 利用ANSYS建立了电视塔的三维有限元模型，通过比较得出的前六阶频率和振型，并说明高阶振型不可忽略。

(2) 讨论了脉动风速时程的模拟方法，针对电视塔的结构几何特性，并借助于MATLAB软件，应用谐波合成法编写风速程序模拟了各层质点的脉动风速时程。根据模拟风荷载的方法，为对电视塔的风振响应及主动控制研究提供了风荷载。

(3) 介绍了形状记忆合金主动控制方法和编制了相应的线性二次型(LQR)经典最优控制算法，然后对有无主动控制作用下该电视塔风振响应进行数值计算。

(4) 对比分析了电视塔在有无控制下的结构位移、速度、加速度和内力响应。结果显示，形状记忆合金控制方法可以有效地减小结构的风致响应，对于高耸结构的风致振动控制是一种较好的主动控制方法。此外，对于该控制系统的稳定性、可靠性尚需进一步深入研究。

[1] 张相庭.结构风工程:理论规范实践[M].北京：中国建筑工业出版社,2006.

[2] 张志强,李爱群,何建平,等.高振型对合肥电视塔风振响应的影响分析[J].特种结构,2004,21(3):42-49.

[3] 刘学利，金建新，王肇民.钢结构电视塔风振反应的高振型影响[J].四川建筑科学研究，1998(1):25-27.

[4] 张文福，孙晓刚.大庆电视塔有限元分析[J].油气田地面工程，2006，25(12):32.

[5] 张志强．合肥电视塔风振及地震响应的振动控制研究[D].南京:东南大学，2003.

[6] 唐振兴.高耸通信塔抗风性能分析[D].长沙:湖南大学，2011.

[7] 周日亘毅，顾 明，朱乐东.广州新电视塔模型测力风洞试验及风致响应研究Ⅱ:风致响应分析[J].土木工程学报，2009，42(7)：14-19.

[8] 罗书泉.高耸电视塔的风振响应及控制分析[D].西安：西安建筑科技大学，2010.

[9] Harris R I. The nature of wind, the modern design of wind-sensitive structures[C]//Construction Industry Research and Information Association， London: 1971.

[10] Roorda J. Tendon control in tall structures[J]. Journal of Structural Division, 1975,101(3):505-521.

[11] 王肇民.钢结构电视塔振动控制及其工程实践[J].特种结构，1998，15(3):1-5.

[12] 陆 飞,程文嚷,李爱群.南京电视塔风振主动控制的实施方案研究[J].东南大学学报，2002，32(5):799-803.

[13] 何敏娟，马人乐.336m黑龙江广播电视塔悬挂水箱振动控制及其实测[J].建筑结构学报，2001,22(1):39-41.

[14] 汪大洋，孙作玉，赵桂峰.高层结构风振失舒率的模糊概率评价[J].水利与建筑工程学报，2013,11(4):28-33.

[15] 马 骏.工业厂房风场数值模拟和抗风优化[J].水利与建筑工程学报,2015,13(1):187-192.

Active control of Wind-induced Vibration of a Television Tower

CHENG Yi

(CollegeofCivilEngineering,YangoCollege,Fuzhou,Fujian350108,China)

Wind is one of natural disasters for television towers, and active control method could effectively mitigate the wind-induced vibration of the television tower. A television tower was taken as an example in this study, the dynamic characteristic of the television tower was firstly analyzed based on the ANSYS software. Subsequently, the stochastic wind field was simulated by the harmonic synthesis. Also, a shape memory alloy (SMA) control method was selected and the numerical simulation of a classical linear optimum LQR control algorithm was established. Finally, the control effects of wind-induced responses of the tower structure with and without the SMA control method were compared. The results shows that the control method can effectively reduce the wind-induced vibration of tower structures.

television tower; dynamic characteristic; fluctuating wind field; wind-induced vibration; active control method

10.3969/j.issn.1672-1144.2016.06.044

2016-07-29

福建省中青年教师教育科研项目(JAT160627)

程 怡(1986—)，女，福建福州人， 讲师，主要从事建筑结构风工程方面的研究工作。E-mail: 84342523@qq.com

TU311.3

A

1672—1144(2016)06—0227—08