生猪养殖场的经营策略优化模型
2017-01-11李珊珊陈俊桦崔祥祥先华翔
冉 玮,谭 兵,李珊珊,陈俊桦,崔祥祥,先华翔
(西南石油大学理学院,四川 成都 610500)
生猪养殖场的经营策略优化模型
冉 玮,谭 兵,李珊珊,陈俊桦,崔祥祥,先华翔
(西南石油大学理学院,四川 成都 610500)
本文建立了基于盈亏平衡的生猪养殖场经营策略模型,利用Matlab软件编程求解,给出基于盈亏平衡的养殖场最优经营策略方案。基于市场价格波动情况,建立了养殖场通过决定留种数量、配种时间、存栏规模等优化经营策略以提高盈利水平的优化模型,给出了最优经营策略。为养殖场的经营管理提供了重要的参考价值。
盈亏平衡;生猪养殖场;优化模型;经营策略
对于生猪养殖业来说散养的饲养方式已经难以适应现在猪肉产品市场的需求。高品质的大量猪肉需求要求我国生猪饲养方式向专业化、集约化和规模化饲养方式进行转变。发展生猪规模化饲养能够提高产品质量并且降低饲养成本。本文考虑以可持续发展理论、规模经济理论等为基础,建立使生猪养殖场效益最大的数学优化模型,给出养殖场的最优经营策略方案。
1 问题假设
假设生猪养殖场的母猪每年只生一胎;小猪在生长过程中不存在死亡或丢失情况且所有肉猪均能售出;假设同一批小猪体重相同、同一批肉猪出售时的品种、体重一致,市场价格相同;假设所有育龄母猪在生育第二胎前第一胎的肉猪全部出售,两胎不重叠;假设从母猪配种到所产的猪仔长成肉猪出栏需要约9个月时间。
2 符号说明

符号意义 符号意义T1一头母猪生一胎的养殖饲料投入 T2猪从出生到入栏平均每千克的成本T3每头种猪从出生到育龄的总成本 a 肉猪出栏时的单位价格m 肉猪出栏时的平均重量 r 小猪转化成种猪的比例x 每头母猪每胎的产仔数 s 一头母猪一生总共能够生产的胎数k 存栏母猪数 g 种猪更新率
3 模型建立与求解
3.1 基于盈亏平衡的生猪养殖场的年平均产仔量
要计算达到或超过盈亏平衡点的年平均产仔量,关键是建立收支平衡方程。首先,从收入与成本两个角度出发,分别构建收入、成本与母猪存栏数、母猪产仔量以及种猪比例等因素的关系,然后求出每头母猪每年平均产仔量与各种成本参数以及生猪价格参数之间的关系。假设不考虑出售猪苗,则在所有环节中只有肉猪处于盈利状况。成本主要包括每头母猪每个怀孕周期的成本、每头肉猪从出生到出栏所需要的成本、每头种猪从出生到育龄的成本、以及期间的人工费用及猪圈折旧等,从而利用收入恰好等于成本,计算得到母猪年均产仔量。
本文以一头母猪一个怀孕周期为单位来考虑,设一头母猪一个怀孕周期(一胎)的养殖饲料投入为T1,每头肉猪从出生到出栏所需的总成本为R1,每头种猪从出生到育龄的总成本R2,肉猪出栏时的总收入为Z1,则达到收支平衡需满足:
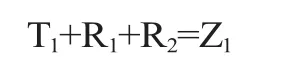
其中,肉猪数目:M1=x(1-r);肉猪成本:R1=mT2x (1-r);种猪数目:M2=xr;种猪成本:R2=xrT3。
为满足达到或超过盈亏平衡点,建立收支平衡方程:
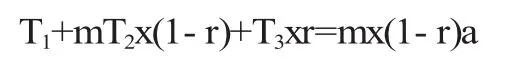
若一头母猪一生总共能共产s胎,公猪与母猪的比例为1∶t,则留种作为的母猪数量:头,留种作为的公猪数量:头。因此,肉猪数目:M1=x·[1-肉猪成本种猪数目:);种猪成本:)。因而,建立新的收支平衡方程[1]如下:T1+mT2
根据市场调查研究以及查阅相关资料得到有关数据,t=25,m=110,母猪一个怀孕周期的养殖T1=3300(元),每头肉猪从出生到出栏时猪肉的成本为T2=14(元/kg),每头种猪达到育龄时的成本T3=1500(元),每头肉猪出栏时的单价a=17.52(元/kg)。
若按每头母猪每年生育两胎,生育期为五年,则s=10,假设生猪养殖成本及生猪价格保持不变,且不出售猪苗,小猪全部转为种猪与肉猪,要达到或超过盈亏平衡点,代入相关数据进行计算得到每头母猪每年至少产仔17.28头。
3.2 养殖场规模达到饱和时,小猪选为母猪的比例及母猪的存栏数
当养殖场养殖规模达到饱和时,本文给出小猪选为种猪的比例和母猪的存栏数。假设生猪养殖场的总栏数为定值10 000。养猪场在养殖规模达到饱和时,应该有公猪、母猪、小猪三种,同时,我们需保证种猪的更新数与后备数相等。假设生育期母猪每头年产2胎,所有育龄母猪在生育第二胎前第一胎的肉猪全部出售,即两胎不重叠,单批的养殖周期为半年。设母猪存栏数为k,种猪的更新率为g。
3.3 基于盈利达最大的生猪养殖场最佳经营优化模型
本文基于生猪价格预测曲线来制定养殖场经营策略,计算未来三年内的平均年利润。利用最小二乘法对猪肉价格与饲料价格的关系进行拟合,得到两者间的函数关系,以总盈利最大为目标,并根据题目要求建立约束条件,建立优化模型,求解得到未来三年内的平均年利润和经营策略。
根据资料,我们对2002年至2008年这12年间的饲料价格和销售价格进行了统计,详细数据如表1:
我们对猪的饲料价格和销售价格利用最小二乘法进行拟合,最终拟合得到销售价格y与饲料价格x的拟合函数关系式为:y=2.4x+7.3,这样我们可根据未来三年的销售价格求解饲料价格。
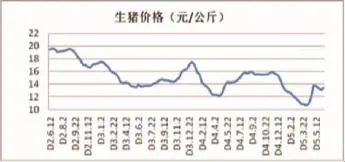
图1 未来三年肉价随时间的变化
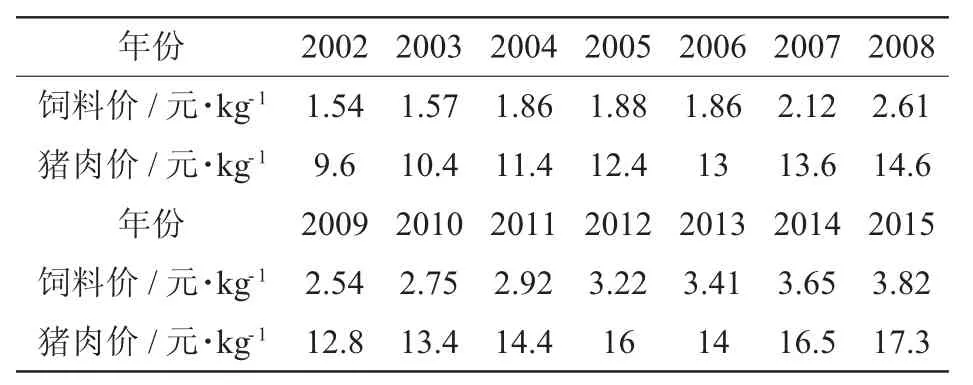
表1 饲料价和猪肉价随时间变化情况
根据未来三年生猪销售价格变化曲线图1,曲线中我们从D2-6-12到D5-6-12每间隔10天进行统计,对这109个点进行了提取,共得到109个时间点对应的销售价格。因此可以根据饲料价格和销售价格的关系式,我们对这109个销售价格对应的饲料价格进行了求解,并根据求解后的数据画出了未来三年饲料价格变化的预测曲线:
通过以上的数据准备,我们对该养殖场的总收支情况进行求解。考虑到母猪产仔具有同步性,并且为了防止出现爆棚现象,一次出售将卖掉所有肉猪,因此在建立目标前我们对第m批肉猪是否在第n个时间点出售和第m批小猪是否在第n个时间点出生分别建立“0-1”变量:

图2 未来三年销售价格随时间的变化
通过分析肉猪价格变化曲线,不难看出在第二个时间点上肉猪销售价格高,因此将原有的这一批肉猪在第二个时间点进行销售,因此该养殖场的总收入为:

图3 未来三年饲料价格随时间的变化

生猪的日饲料消耗量和饲料价格确定生猪养殖成本为:
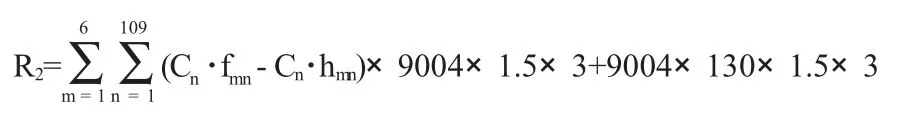
对于种猪饲养成本,我们根据对种猪销售价格和拟合关系式求解种猪饲料价格,再根据饲料价格和生猪数量确定该养殖场种猪养殖成本:
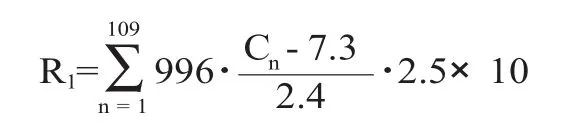
假设肉猪从出生到出栏至少要160天,两次销售时间间隔不少于180天,本文以该养殖场总利润达最大为目标,建立如右优化模型:

利用lingo软件进行求解,得到该养殖场未来三年的年均利润为586.949万元,根据计算结果和未来三年肉猪售价变化曲线给出的时间,得到生猪养殖场的最优经营策略如表2。

表2 养殖场的最佳经营策略
4 结论
本文结合市场实际生猪养殖的生产情况以及相关文献,建立相应的收支平衡模型以及最优经营策略模型,求解出生猪养殖场相关的优化方案。利用收支平衡建立盈亏平衡模型,考虑生猪养殖场的养殖规模、存栏数及市场价格,建立使生猪养殖场盈利达最大的优化模型,进而求解得出了最佳经营策略。本文对于生猪养殖场的经营具有一定的参考意义。
[1]吴孟达,李银飞.生猪养殖场的经营管理策略研究[J].数学建模及其应用,2014,(4).
(编辑:晏兵兵)
F326.3
A
1006-799X(2016)21-0036-03
西南石油大学大学生课外开放重点实验项目资助(KSZ15149)。
冉 玮(1995-),女,四川万源人,在读本科生,主要研究方向为应用数学。
