镜像延拓EMD方法的改进及其应用

李鹏鹏，冯武卫,2，张玉莲，王 琴

（1.浙江海洋大学船舶与机电工程学院，浙江舟山 316022；2.浙江省近海海洋工程技术重点实验室，浙江舟山 316022；3.扬帆集团股份公司，浙江舟山 316101）

镜像延拓EMD方法的改进及其应用

李鹏鹏1，冯武卫1,2，张玉莲1，王 琴3

（1.浙江海洋大学船舶与机电工程学院，浙江舟山 316022；2.浙江省近海海洋工程技术重点实验室，浙江舟山 316022；3.扬帆集团股份公司，浙江舟山 316101）

希尔伯特黄（Hilbert-Huang）变换是一种自调节信号分解方法，通常该方法包括两部分：经验模式分解（Empirical Mode Decomposition，EMD）和希尔伯特变换。由于希尔伯特黄变换理论并不成熟，尤其是该方法存在的“端点效应”问题，使其在某些场合应用误差较大。为了解决端点效应问题，本文首先从阐述了Hilbert-Huang变换的基本理论、算法、存在的问题及常见的解决方法入手，针对镜像闭合延拓EMD处理端点效应问题时的不足，提出了一种新的镜像延拓EMD方法。最后利用仿真信号验证了该方法的有效性，取得了较好的结果。

Hilbert-Huang变换；经验模式分解；故障诊断系统

船舶机械设备运行过程中存在着诸多的非平稳信号，例如船用发动机旋转设备在升降速过程中的摩擦、基座松动、不对中、裂纹、旋转失速、油膜涡动和油膜振荡等故障，其轴承径向振动信号都表现出非平稳性。因此对非平稳信号处理方法的研究已经成为船用机械设备状态监测及故障诊断的研究热点之一。在1998年，Norden E.Huang等人提出了一种自适应的Hilbert-Huang变换信号处理方法，该方法是近年来对以傅立叶变换的基础的线性和稳态谱分析的一个重要突破。

与其它信号处理方法相似，当利用Hilbert变换分解信号时，信号两端端点效应问题较为突出。如果信号序列较长，可以在分解过程中不断丢弃端点数据来确保分解结果的误差最小，而如果信号长度较短，上述方法将无法操作。对于上述问题，Norden E.Huang提出了根据原始信号波对两端数据进行适度延拓以改善端点效应的办法，此方法对减小端点效应的影响效果显著。针对希尔伯特变换中存在的端点效应问题，信号处理领域学者做了深入的研究，提出了许多卓有成效的方法。在2001年，赵进军等[1]提出了镜像闭合延拓算法。该算法把原数据序列对称地延拓成一个封闭的环形数据，再对环形数据进行EMD分解。2004年，刘慧婷等[2]运用多项式拟合方法进行信号延拓。该算法利用信号极值点数据序列端点处的几个极值点求出拟合多项式，从而得到极值点序列在端点处的近似值，然后预测信号的极值包络。2005年，邓拥军等[3]将神经网络技术应用于信号延拓过程中，通过大量实验验证，该算法适应性强，抑制端点效应效果明显。然而实际应用中，该方法需要根据不同的信号设定不同类型的神经网络模型，同时神经网络的计算速度差，学习、结构和类型的选择过分依赖于经验等固有缺陷都限制了该算法的通用性。同年，程军圣，于德介等[4]提出一种新的延拓算法：基于时变参数ARMA模型延拓的算法，该算法的基本思想与基于神经网络技术延拓的算法类似，但该算法在对非线性信号进行延拓时，会产生较大的预测误差。

虽然目前已有大量解决端点效应的方法，但从实际应用结果上看，端点效应仍未得到较理想的解决，而该问题是制约EMD方法分解结果的精确性，限制希尔伯特黄变换应用的的最棘手的问题，因此本文对该问题进行深入的研究，提出一种改善的镜像延拓方法，通过仿真信号的分析，验证了本文方法的有效性。本文方法可应用于各类旋转机械，如船舶机械、水产加工机械、港口起重机械等各类大型设备故障检测与信号处理。

1 EMD方法实现过程

EMD是将信号分解为固有模式函数集合表示的方法。对任意实信号x(t)进行经验模式分解的具体过程如下：

首先计算出信号x(t)的所有局部极值点，然后连接所有局部极大值点和所有极小值点，连接过程可以采用数据拟合的方法，记局部极大值点曲线为上包络线fmax(t)和局部极小值点为下包络线fmin(t)。记fmax (t)和fmin(t)的平均值为m(t)，x(t)与m(t)的差记作h(t)，即：

在理想情况下，h(t)可以作为一个IMF，因为h(t)的构造过程就是使它满足IMF的两个条件。但是由于实际信号复杂性，一般情况下h(t)不是一个平稳的数据系列。因此将h(t)视为新的x(t)，重复以上操作，直至当h(t)满足一定的固有模式函数判据（如上下包络线平均值趋近于零）时，记：

将c1视为一个IMF，再作：

将r(t)视为新的x(t)，重复上述过程，然后依次获得第二个IMF和第三个IMF，……。当cn或r(t)满足给定的筛分停止条件（如残余函数r(t)足够小或r(t)成为单调函数）时，筛分过程终止，最终分解式可描述为：

式中r(t)称作残余函数，表示信号平均变化趋势。

EMD程序流程如图1所示。

图1 EMD程序流程图[5]Fig.1 EMD program process chart[5]

2 改进的EMD算法

针对EMD方法存在的端点效应问题，目前已有多种解决方法[6-10]。但是EMD目前仍缺少严密的数学证明，对分解结果也缺少评价指标，因此仍很难说明何种方法更好。因此本文对该方法加以改进和晚上，提出了一种改进的镜像延拓EMD处理方法。

本文方法的计算过程如下：①计算原始信号的局部极值；②对新的极值序列进行对称延拓；③比较原信号的端点与延拓后新的极值点；④针对新生成的序列，以左端点为对称面进行镜像延拓；⑤采用上述EMD算法过程进行信号分解；⑥根据原始信号的起始点位置和长度，对新的信号分解结果进行截断。整个算法详细的计算过程可描述为：

（1）首先计算原始信号x(n)，n=1，2，……，N的局部极值点，如图2所示。

图2 原始信号及其极值点Fig.2 Practical signal and its extremum points

令信号的局部极大值点序列为：

局部极小值点为：

（2）对信号按公式（7）进行极值点对称延拓，从而得到新的极值点：

（3）对延拓得到的新序列进行修正：

当端点值满足公式(8)，则表示原始信号的端点即为极值点。否则，需要利用新的极点对信号进行镜像延拓。设镜像延拓和处理后信号为xyan(i)，i= 1，2，……，nyan，运算过程中需要保留原始信号在信号中的起点和数据长度，分别设为xstartyan和len。图3给出了利用本文方法得到的延拓结果。

（4）采用信号的左端点作为对称面，按公式(9)对信号进行镜像延拓，得到用于经验模式分解的新信号xnew(i)，i=1，2，……，nnew：

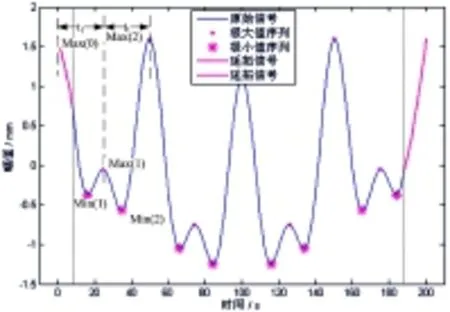
图3 信号对称延拓及修正后得到的新信号xyanFig.3 Obtained new signal xyan by extending and revising

同时，更新原始信号在新信号中的起点位置xstartnew=xstartyan+nyan-2。镜像延拓结果如图4所示。

图4 信号镜像延拓结果Fig.4 Signal mirror extending results

3 仿真信号研究

为了验证本文的改进镜像延拓EMD的效果，分别使用以端点为极值点的EMD（以下简记为NEMD）、镜像闭合延拓EMD（以下简记为MEMD）和改进镜像延拓EMD（以下简记为IMEMD）三种方法进行分解，对式（10）所示仿真信号进行分析：

式（10）所示仿真信号由三个余弦信号线性叠加组成，采样率为1。三种方法的分解结果如图6所示所示，从图6所示结果，可以看出MEMD和IMEMD均分解得到了三阶IMF分量，分别对应仿真信号中三个余弦信号分量，而NEMD方法只分解得到了两阶IMF分量。且NEMD分解效果不好，而MEMD和IMEMD分解效果均比较好。为了更一步比较MEMD和IMEMD两种方法的分解效果，将两种方法的各阶IMF分量与仿真信号中的信号分量进行对比，如图7所示，从图7可以看出，对第1、2阶IMF，在两个端点处IMEMD均比MEMD翘曲更小，与真实信号分量更接近。对第3阶IMF，MEMD得到的结果是一个单调信号，不能反应出真实信号分量的变化趋势，而IMEMD能够反应出这种变化趋势，均为半个周期的正弦型信号，因此IMEMD比MEMD能够更好的处理端点效应问题。为了更进一步的评价分解结果与真实信号间的误差，定义相对误差判据如式（11）所示。

图6 三种处理方法分解结果Fig.6 The results of three processing methods

图7 MEMD和IMEMD分解结果对比图Fig.7 The results of comparing MEMD and IMEMD

其中xi(t)是原始信号中的第i个高频分量成分，对上面两种方法的分解结果分别计算相对误差得：

从表1中可以看出，IMEMD与MEMD相比，各阶IMF与真实信号之间的相对误差都更小，由此可以看出IMEMD可以更好的削弱端点效应对结果的影响。由于IMEMD在MEMD的基础上增加了极值点对称延拓处理，所以端点的位置直接影响到IMEMD的分解结果，当信号的端点满足式（8）时，表示信号的端点可以直接作为极值点，此时不进行延拓，IMEMD与MEMD相同。为了说明信号的端点对IMEMD分解结果的影响，下面仍以式（10）所示信号为例，保持右端点不变，左端点起始位置取1～11，使用MEMD和IMEMD进行分析并计算相对误差，结果见表2。

限于篇幅，上表只列出了其中的4组分析结果。从表2可以看出对不同端点位置的信号，IMEMD均比MEMD相对误差较小。为了便于对比两种方法的相对误差，将上表的结果绘制相对误差对比图如图8所示。

图8 MEMD和IMEMD分解结果相对误差对比Fig.8 The error of comparing MEMD and IMEMD

上图横坐标为信号的左端点位置，从1到11。从图8中可以看出，端点位置从1到5时，两种方法的所得结果的相对误差比较接近，IMEMD只比MEMD略好一点。但是端点位置从6开始时，MEMD出现了较大的相对误差，而IMEMD的相对误差一直较小。特别是第3阶IMF，MEMD的误差较大，已不能获得正确的分解结果。对大量信号进行分析，结果显示IMEMD能够较好的抑制端点效应对结果的影响，尤其是当信号端点不是极值点时，IMEMD比MEMD分解结果更好。

表1 MEMD和IMEMD分解结果相对误差Tab.1 The relative error of comparing results with MEMD and IMEMD methods

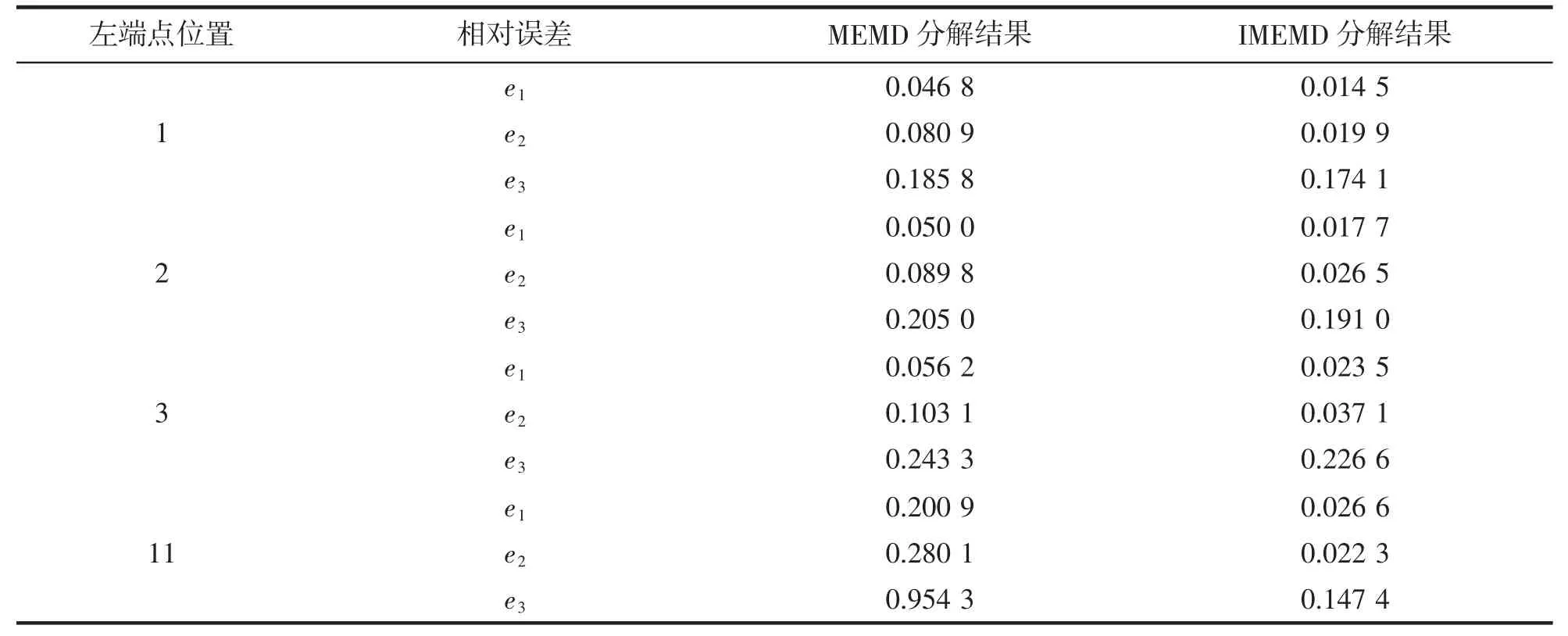
表2 不同端点位置的信号MEMD和IMEMD分解结果相对误差Tab.2 The relative error of MEMD and IMEMD methods with different endpoint location

4 结论

本文针对EMD的端点效应，结合已有的极值点对称延拓和镜像闭合延拓方法，提出了改进镜像延拓EMD，并以仿真信号对该方法的有效性进行了检验，结果表明该方法能够较好的解决端点效应问题。最后将EMD应用于特征信号提取和旋转机械稳定性分析，取得了良好的结果。

[1]赵进平.异常事件对EMD方法的影响及其解决方法研究[J].青岛海洋大学学报,2001,31(6):805-814.

[2]刘慧婷,张 旻,程家兴.基于多项式拟合算法的EMD端点问题的处理[J].计算机工程与应用,2004(16):84-86.

[3]邓拥军,王 伟,钱成春,等.EMD方法及Hilbert变换中边界问题的处理[J].科学通报,2001,46(3):257-263.

[4]程军圣.基于Hilbert－Huang变换的旋转机械故障诊断方法研究[D].长沙:湖南大学,2005.

[5]HUANG N E,SHEN Zheng,LONG S R,et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time SeriesAnalysis[J].Proceedings of the Royal Society of London,1998(454A):903-995.

[6]盖 强,马孝江,张海勇,等.几种消除局域波法中边界效应的新方法[J].大连理工大学学报,2002,42(1):115-117.

[7]CHEN Q H,HUANG N E,RIEMENSCHNEIDER S,et al.A B-spline approach for empirical mode decompositions[J].Advances in Computational Mathematics,2006(24):171-195.

[8]钟佑明,秦树人,汤宝平.一种振动信号新变换法的研究[J].振动工程学报,2002,15(2):231-238.

[9]MALLAT S G.Multiresolution Appoximation and Wavelet Orthonomal Bases of L2[J].Trans.AMS,1989(315)：69～87.

[10]MALLAT S G.A Theory for Multiresolution Signal Decomposition:The Wavelet Representation[J].IEEE Trans,On Pattern Analysis and Machine Intelligence,1989(11):693-874.

Study of Improved Mirror Extending EMD Method and Application

LI Peng-peng1,FENG Wu-wei1,2,ZHANG Yu-lian1,et al
(1.School of Ship and Mechatronics Engineering,Zhejiang Ocean University,Zhoushan 316022; 2.Key Laboratory of Offshore Engineering Technology of Zhejiang Province,Zhoushan 316022,China)

HHT is presented is an adaptive signal processing method.There are two steps in the HHT, which is Empirical Mode Decomposition (EMD)and Hilbert transform.Because of the HHT theory is not mature,especially it’s boundary effect problem,which will result in large error in some fields.In order to solve the boundary effect problem,this paper firstly introduces the sifting process of the EMD,some problems and solved methods.The Mirror Extending EMD is a method to solve the boundary effect problem of EMD,but there are some problems of this Method.An improved Mirror Extending EMD(IMEMD)is presented by this paper.Then he simulative signal verified the effectiveness of the new method and achieved good results.

Hilbert-Huang Transform;EMD;fault diagnosis system

TH201

A

1008－830X(2016)03－0244－05

2016-03-05

国家自然科学基金面上项目（51379189）；中央财政支持地方高校发展专项海洋工程装备创新团队资助项目；浙江省科技厅重大专项社会发展项目（2013C03031）

李鹏鹏（1978-），女，山西运城人，硕士研究生，研究方向：机械故障诊断.

冯武卫，男，副教授.E-mail:fengwuwei@163.com