舵系统流激振动影响因素及规律的理论与试验研究

肖清，胡刚义，谢俊超

中国舰船研究设计中心，湖北武汉430064

舵系统流激振动影响因素及规律的理论与试验研究

肖清，胡刚义，谢俊超

中国舰船研究设计中心，湖北武汉430064

流激舵系统引起的振动对水下航行体隐蔽性产生较大影响。为深入研究其振动特性，根据舵系统的结构组成进行简化，建立系统二元线性颤振数学模型，确定低速颤振的产生条件，并获得低速颤振的主要影响因素和作用规律。此外，在重力式水洞中开展舵模型流激振动试验，重点研究了支撑刚度、扭转刚度、质心和刚心位置等参数变化对舵模型流激振动的影响。结果表明：在流体载荷激励下，舵系统结构设计对流激振动特性有较大影响，通过对升沉运动与扭转运动频率之比、结构质量与附加质量之比、刚心、质心与弦中心的相对位置等参数进行匹配设计，能够有效抑制舵系统流激振动。

舵系统；流激振动；低速颤振；水洞

0 引 言

舵作为水下航行体的突出体，在航行过程中不可避免地受到流体激励而产生振动，这种振动将不利于舵及其传动系统的正常工作，且对水下航行体的隐蔽性产生影响［1-3］。

通过开展相关研究，国内外关于舵翼等在流体中的弹性力学计算理论，已基本成熟［4-6］。对于舵叶等机翼、水翼的流激振动也开展了大量的计算与试验研究［7-11］。本文将在上述研究的基础上，针对一类具有小厚度、小拱度、小展弦比的舵叶及其传动系统等开展研究，通过理论分析与试验，研究影响舵系统流激振动的因素及其作用规律，可为工程设计提供一定的指导。

1 舵系统流激振动理论分析

某水下航行体舵系统的结构如图1所示，包括舵叶、舵轴、滑动轴承、舵柄、导向拉杆、导向装置、传动杆、液压压机等。其中，舵面一般为空心变截面结构，舵轴通过与轴套配合，由卡环固定其轴向移动，通过伺服舵柄操纵舵面偏转。

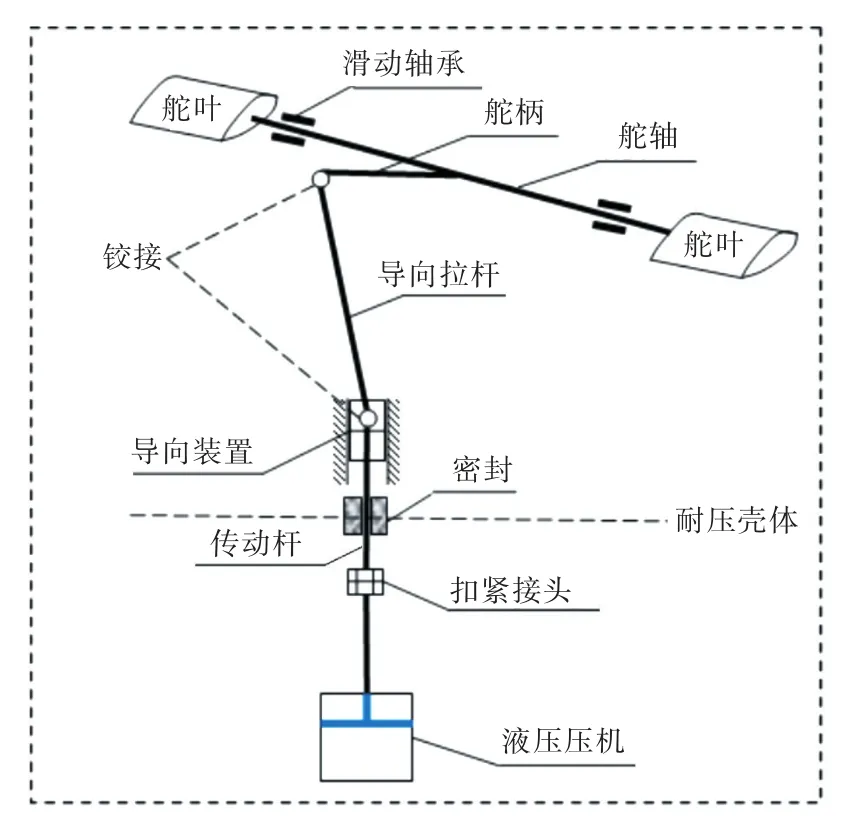
图1 舵系统示意图Fig.1 Schematic of the rudder system

对于液压伺服机构，假设间隙、液压和反馈回路只影响系统的升沉和扭转刚度。舵轴和液压伺服机构可简化为一根当量梁B′B，其中B′和B与舵面连接；安装有轴承的A′和A两端处理为弹性支撑点，约束舵轴的升沉运动；舵柄与舵轴连接点O处理为弹性扭转固定端点，约束绕舵轴的扭转运动（图2）。

图2 舵振动力学模型Fig.2 Vibration dynamic model of the rudder system

将舵轴和舵叶视作一个刚体系统；将安装有轴承的A′和A两端等效为2个支撑弹簧，其升沉刚度为kh；而将舵柄与舵轴连接点O等效为1个扭转弹簧，其扭转刚度为2kα。在流体动力激励下，舵叶与舵杆系统有2个自由度的运动：一个是舵叶与舵杆系统的升沉运动，位移为h，向下为正；另一个是舵叶绕舵轴扭转转动，转角为α，迎流抬头为正。

升沉位移h和转角α满足如下两自由度运动方程：

式中：系统质量为2m；系统质量静矩为2Sα；系统转动惯量为为系统扭转自然频率；为系统升沉自然频率；L为单个舵叶的水动升力（向上为正）；M为单个舵叶的俯仰力矩（迎流抬头为正）。

当水下航行体航速等于颤振速度时，舵叶和舵杆系统以颤振频率ω作简谐振动，即

相应的升力及俯仰力矩可写为

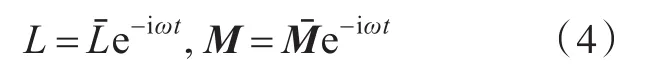
将式（3）和式（4）代入式（1）和式（2），可得：

对具有小厚度和小拱度无限展长的水翼，当其在给定攻角的不可压缩来流中做简谐升沉及扭转运动时，其非定常水动升力和俯仰力矩可由Teodorsen理论给出。但本研究的舵系统属于具有小厚度和小拱度的小展弦比水翼，在计算其非定常水动升力和俯仰力矩时，需要考虑舵叶的三维效应，即需要对Teodorsen理论进行修正。

设水的密度为ρw，舵叶半弦长为b，展长为l，为舵叶剖面中心到刚心（转轴位置）的距离占半弦长的百分比，如刚心在舵叶剖面中心后方，则为正（图3）。那么，对有限展长舵叶，其水动升力及俯仰力矩可表示为

图3 有限展长舵叶水动计算模型Fig.3 Hydrodynamic calculation model of the limited span rudder

式（8）～式（11）中，各参数如下：

其中：AR为展弦比；τ为形状参数（与AR有关），如图4所示。

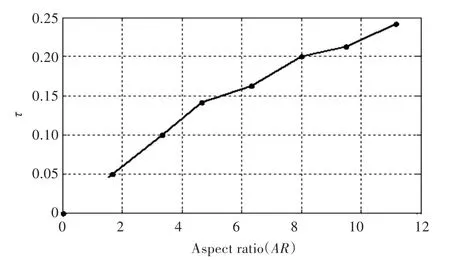
图4 展弦比AR与形状参数τ的相关关系Fig.4 Relationship betweenARandτ

将式（5）和式（6）写成矩阵方程

v-g法是颤振分析的最常用方法之一。在这个方法中，首先假设系统阻尼为零，然后在系统运动方程中引入人工阻尼，这时式（17）变为

用v-g法做颤振分析的具体方法如下：

1）通过求解广义特征值问题（式（20）），得到g,v,ω随k的变化函数，画出v-g和v-ω函数；

2）当g=0时，系统处于临界状态，正好出现颤振，此时的v即为颤振速度vF，而ω则为颤振频率；

3）当g＜0时，系统是稳定的，没有发生颤振；

4）当g＞0时，系统是不稳定的，已经发生了颤振。

水下航行体颤振通常发生在质量比较小的情况，此时，当流速小于颤振速度，系统就已经是发散的，因此这类颤振通常对低速航行体是危险的。水下航行体舵属于低质量比系统，其舵颤振属于低速颤振问题。

2 水下航行体舵叶颤振特性分析

2.1 分析参数

根据上述计算理论，通过对某水下航行体舵叶进行建模计算，并对整个简化舵系统进行湿模态计算，可得颤振计算所需的如下参数：

1）展长：l=3.19 m；

2）舵叶质量+水质量+内部舵轴质量：mtotal= 3 202 kg；

3）3/4翼展处半弦长：b=0.9 m；

4）质心所在位置处翼段的半弦长：bcg= 1.043 5 m；

5）单位展长的质量：m=mtotal/l=1 003 kg/m；

6）质心到中心的距离的无量纲量值：εcg=-0.157 7；

7）刚心到中心距离的无量纲量值：a=-0.48；

8）刚心到质心距离的无量纲量值：xa=0.322 3；

9）单位展长舵叶对刚心的质量静矩：Sα=291.16 kg；

10）单位展长舵叶对刚心的质量惯性矩可以约等于：Iα=371.3 kg·m；

11）舵叶对刚心的无量纲回转半径：rα=0.583；

12）频率比的无量纲量值：Rω=ωh/ωα；

13）无量纲质量μ=m/(πρwb2)=0.395。

对于线性颤振计算，共有5个无量纲参数，分别是a，μ，rα，xa，Rω。它们的初始值分别为：a=-0.48，μ=0.395，rα=0.583，xa=0.322 3，Rω= 0.549 9。

2.2 特性分析

通过对舵系统颤振特性理论分析可知，舵系统的升沉和扭转刚度、舵叶压力中心、刚心和质心三者的相对位置，以及舵的集中质量和附加质量的比值对舵低速颤振有较大的影响。为研究这些因素对舵低速颤振的影响规律，根据舵低速颤振计算模型，分别改变a，μ，rα，xa，Rω的值，计算颤振速度。

从图5和图6可以看出，当xa为-0.2和0的时候，都未发生颤振，说明质心与刚心重合或质心在刚心前面，当无量纲质量比μ在0～50范围内变化，不会发生颤振。

图5 速度—人工阻尼图（xa=-0.2）Fig.5 Relationship between velocity and artificial damping（xa=-0.2）

图6 速度—人工阻尼图（xa=0）Fig.6 Relationship between velocity and artificial damping（xa=0）

由图7可知，当xa减小时，可以有效提高颤振临界速度，当xa减小到一定程度时，将很难发生颤振。此外，每一条曲线都存在一个极小值μm。当μ≤μm时，随着μ→0，颤振速度将以非常陡的斜率上升，较难发生颤振。当μ＞μm时，随着μ的增大，颤振速度将缓慢增大，较容易发生颤振。由此可知，一般情况下，对于给定的结构，m和ωα不变，舵在高密度的介质中的质量比较小，几乎没有颤振的危险。

由图8可见，当频率比Rω在1左右时，颤振速度接近最小。若增加ωα而保持Rω不变，则vF将与ωα成正比增加。当Rω＜1时，如果单独增加ωα，则因Rω减小而使vF的值将有更大的增加。若增加ωh，则当Rω＜1时，vF也相应减小。由此可见，对这时的参数组合，颤振的主要模态是扭转模态，即扭转分支首先变得不稳定，因此，增加扭转刚度可以使颤振速度大幅提高。此外，由图可见，质心相对刚心位置的无量纲量xa前移可提高vF。通常可以采用在水翼前缘增加配重来使得质心前移。

图7 质量比μ对颤振速度的影响规律图（rα=1.06，Rω=0.972 2）Fig.7 Influencing rules of mass ratio to flutter velocity（rα=1.06，Rω=0.972 2）

图8 频率比Rω和xa对颤振速度的影响规律图（rα=1.06,μ=20）Fig.8 Influencing rules of frequency ratio to flutter velocity（rα=1.06,μ=20）

3 舵系统流激振动试验研究

为进一步研究各因素对舵系统流激振动的影响，在上述基础上开展舵系统流激振动试验研究。

3.1 试验模型

试验模型由舵叶、轴和台架3个部分组成。

考虑2个舵叶模型，一个为等截面舵叶，另一个为非等截面舵叶。等截面舵叶模型为NACA0017翼型，使用不锈钢制作，蒙皮为0.5 mm，弦侧为1 mm，沿展长1/4，1/2，3/4处分别用1 mm肋支撑。

舵叶型线图如图9所示，舵叶的具体参数如表1所示，其中，刚心在弦中点之后时＞0，质心在刚心之后时xa＞0。

图9 等截面舵叶型线Fig.9 Molded lines of the constant cross-section rudder

表1 等截面舵叶参数Table 1 Parameters of the constant cross-section rudder

非等截面舵叶模型的截面仍为NACA0017翼型，使用塑料制作，内部为空心，可在内部通过重块调节质量和质心等参数，如图10所示。舵叶的具体参数如表2所示。

图10 非等截面舵叶型线Fig.10 Molded lines of the variable cross-section rudder

表2 非等截面舵叶参数Table 2 Parameters of the variable cross-section rudder

试验模型中舵轴承处采用可调式支撑结构进行支撑刚度调节（图11），舵杆处设置4组弹簧进行扭转刚度、舵角的调节，为模拟不同的质心和刚心位置，制作了多组舵结构模型，内部采用空心结构，利用重块调节舵叶的结构质量、质心位置等参数。

图11 试验模型Fig.11 Experimental model

支撑刚度模拟主要是在台架和舵轴结构之间固定有支撑弹簧，舵轴结构内含有轴承从而不会约束舵轴的扭转，当轴在流激作用下进行升沉运动时，支撑弹簧就会产生反力，从而模拟支撑刚度。支撑刚度的大小主要通过改变支撑弹簧的刚度实现。扭转刚度模拟采用了一组垂直于舵扭杆的弹簧组成，并且可以通过调节弹簧到轴系的距离来改变扭转刚度的大小。

3.2 试验条件

利用重力式水洞研究舵—杆模型系统的流激振动特性，测试不同组合工况下试验模型的流激振动响应，掌握舵系统流激振动特性。该水洞工作段长6.0 m，横截面为0.7 m×0.7 m，最高水速5 m/s，流速不均匀度＜1%，紊流度＜0.5%，如图12所示。

图12 重力式水洞Fig.12 Gravitation water tunnel

3.3 试验方法

将试验台架（包括支撑钢片和扭转弹簧等）放置在水洞外，而舵叶放置在水洞中（舵叶距离水洞侧面5 cm）。根据试验要求，调整好舵叶攻角、支撑和扭转刚度，然后开启水洞的水泵，采用比托管记录实验段内的流速，使流速按照一定的间隔从小逐渐增大，记录不同流速下舵杆系统的振动数据。试验模型的振动采用激光测振仪和加速度传感器进行测量。

3.4 试验结果

3.4.1支撑刚度对舵模型振动影响规律

通过调节改变试验台架支撑刚度，根据实际情况选取支撑刚度kh=9.0×104，3.0×105，1.5×106N/m，分别在不同航速下进行舵模型的流激振动试验，其他参数为：α=5°，kα=282（N·m）/rad，=-0.48，xa=0.042 m，测得支撑刚度改变对舵模型振动幅值及频率的影响规律。

由图13结果可知在不同支撑刚度下，舵系统升沉和扭转振动频率随流速的变化特性。由图可知，升沉和扭转振动频率均在各自的固有频率附近变化，即两类流激振动均属于各自固有频率附近的低频振动，并且支撑刚度越大，舵系统的升沉运动频率值越大，扭转运动频率值反而越小。

图13 不同支撑刚度下舵系统运动频率值随流速变化特性Fig.13 The varying characteristics of rudder system motion frequency under different support stiffness

对特定流速v=2.03 m/s时不同支撑刚度下舵叶表面加速度传感器采集到的信号进行快速傅立叶变换，得到频域下的升沉运动加速度变化曲线如图14所示。而对该流速时不同支撑刚度下扭转杆件上加速度传感器采集到的信号进行快速傅立叶变换，得到频域下的扭转运动加速度变化曲线如图15所示。

图14 不同支撑刚度下升沉运动加速度变化（ v =2.03 m/s）Fig.14 The varying characteristics of heave motion acceleration under different support stiffness（v=2.03 m/s）

根据图14和图15分析可知，在相同流速下，支撑刚度越大，舵叶升沉运动和扭转运动的幅值越小，对于一阶升沉运动的影响最大。由此可知，舵叶的支撑刚度对舵叶升沉和扭转运动的影响最大，在一定范围内提高支撑刚度有利于控制舵叶的流激振动。

3.4.2扭转刚度对舵模型振动影响规律

通过调节改变试验台架的扭转刚度，根据实际情况选取扭转刚度kα=282，704，1 348 N·m/rad，分别在不同航速下进行舵模型的流激振动试验，其他参数为：α=5°，kh=1.5×106N/m，=-0.48，xa=0.042 m，测得扭转刚度改变对舵模型振动幅值及频率的影响规律。

图16给出了不同扭转刚度条件下，舵系统升沉和扭转振动频率随流速的变化特性。由图可知，升沉和扭转振动频率均在各自固有频率附近变化，随着扭转刚度的增大，舵系统扭转运动的频率逐渐增大，而升沉运动频率值没有明显变化。

图16 不同扭转刚度下舵系统运动频率值随流速变化特性Fig.16 The varying characteristics of rudder system motion frequency under different torsional stiffness

对特定流速v=2.03 m/s时不同扭转刚度下舵叶表面加速度传感器采集到的信号进行快速傅立叶变换，得到频域下的升沉运动加速度变化曲线如图17所示。而对该流速时不同扭转刚度下扭转杆件上加速度传感器采集到的信号进行快速傅立叶变换，得到频域下的扭转运动加速度变化曲线如图18所示。

图17 不同扭转刚度下升沉运动加速度变化（v=2.03 m/s）Fig.17 The varying characteristics of heave motion acceleration under different torsional stiffness（v=2.03 m/s）

图18 不同扭转刚度下扭转运动加速度变化（v=2.03 m/s）Fig.18 The varying characteristics of torsion motion acceleration under different torsional stiffness（v=2.03 m/s）

根据图17～图18分析可知，扭转刚度的增大对舵叶扭转运动最大幅值有明显的抑制作用，但是升沉运动的第1阶运动幅值则会出现增大。

3.4.3刚心位置对舵模型振动影响规律

通过调节刚心到弦中点的距离，分别在不同航速下进行舵模型的流激振动试验，根据实际情况选取刚心位置=-0.24，-0.48，-0.81，其他参数为：α=5°，kh=1.5×106N/m，kα=282（N·m）/rad，xa=0.042 m，测得刚心到弦中点的距离变化对舵模型振动幅值及频率的影响规律。

在图19中，给出了当α=5°，kh=1.5×106N/m，kα=282（N·m）/rad，xa=0.042 m时，不同刚心位置下，舵系统升沉和扭转振动频率随流速的变化特性。由图可知，升沉和扭转振动频率均在各自的固有频率附近变化，即两类流激振动均属于各自固有频率附近的低频振动，并且总体看来，刚心最靠近导边（=-0.81）是，扭转运动频率值最大，而升沉运动频率值最小。

图19 不同刚心位置下舵系统运动频率值随流速变化特性Fig.19 The varying characteristics of rudder system motion frequency under different stiffness center positions

对特定流速v=2.03 m/s时不同刚心位置下舵叶表面加速度传感器采集到的信号进行快速傅立叶变换，得到频域下的升沉运动加速度变化曲线如图20所示。而对该流速时不同刚心位置下扭转杆件上加速度传感器采集到的信号进行快速傅立叶变换，得到频域下的扭转运动加速度变化曲线如图21所示。

图20 不同刚心位置下升沉运动加速度变化（v=2.03 m/s）Fig.20 The varying characteristics of heave motion acceleration under different stiffness center positions（v=2.03 m/s）

图21 不同刚心位置下扭转运动加速度变化（v=2.03 m/s）Fig.21 The torsion characteristics of heave motion acceleration under different stiffness center positions（v=2.03 m/s）

根据图20～图21分析可知，刚心位置到导边距离的减小对舵叶升沉运动的最大幅值有明显的抑制作用，对扭转运动的最大幅值影响不明显，但是对扭转振动的频率有增大的趋势。

3.4.4质心位置对舵模型振动影响规律

通过调节质心位置，根据实际情况选取质心位置xa=0.03，0.042，0.05 m，分别在不同航速下进行舵模型的流激振动试验，其他参数为：α=5°，kh=1.5×106N/m，kα=282（N·m）/rad，=-0.48，测得质心位置变化对舵模型振动幅值及频率的影响规律。

在图22中，给出了当α=5°，kh=1.5×106N/m，kα=282（N·m）/rad，=-0.48时，不同质心位置下，舵系统升沉和扭转振动频率随流速的变化特性。由图可知，升沉和扭转振动频率均在各自的固有频率附近变化，即两类流激振动均属于各自固有频率附近的低频振动。

对特定流速v=2.03 m/s时不同质心位置下舵叶表面加速度传感器采集到的信号进行快速傅立叶变换，得到频域下的升沉运动加速度变化曲线如图23所示。而对该流速时不同质心位置下扭转杆件上加速度传感器采集到的信号进行快速傅立叶变换，得到频域下的扭转运动加速度变化曲线如图24所示。

根据图23～图24分析可知，相同流速下，质心到刚心的距离越大（质心均在刚心之后），舵叶升沉运动的幅值越大，但是扭转运动的幅值相对降低。因此，质心位置离刚心的距离越小对于控制舵叶的升沉运动越有利。

图22 不同质心位置下舵系统运动频率值随流速变化特性Fig.22 The varying characteristics of rudder system motion frequency under different mass center positions

图23 不同质心位置下升沉运动加速度变化（v=2.03 m/s）Fig.23 The varying characteristics of heave motion acceleration under different mass center positions（v=2.03 m/s）

图24 不同质心位置下扭转运动加速度变化（v=2.03 m/s）Fig.24 The torsion characteristics of heave motion acceleration under different mass center positions（v=2.03 m/s）

4 结 论

通过建立参数可调的舵系统流激振动试验模型，并开展系列试验，发现试验结果与理论计算趋势基本一致。主要结论如下：

1）增大支撑刚度，可以显著减小舵系统升沉振动加速度级幅值，因此在设计中，可以尽可能增大支撑刚度。

2）增大扭转刚度虽然可以降低扭转振动加速度级幅值，但同时也会增大升沉振动加速度级的幅值，因此在设计中，扭转刚度的合理选择很关键，并不是越大越好。

3）刚心位置对舵系统的扭转振动加速度级幅值影响不是很显著，但刚心位置适当向前偏，可以显著减小舵系统的升沉振动加速度级幅值，因此在设计中可以考虑在满足舵系统稳定性及相关水动力和结构性能的前提下，将刚心位置适当向前偏。

4）质心位置对舵系统的扭转振动加速度级幅值影响不是很显著。在低速情况，如果质心适当向前偏一些，则升沉振动加速度幅值可降低。

本研究建立了舵系统流激振动计算模型，开展理论计算，分析舵低速颤振的影响因素和作用规律，并进行流激振动试验，研究舵系统流激振动影响因素及规律，可为工程研制中舵系统流激振动设计提供参考。

但同时也可以看到，由于试验条件有限，模型等效缩尺比例较大，试验系统中还存在着间隙、摩擦等非线性因素，无法完全等效处理，对试验结果产生了一定的影响，试验结果与理论计算尚无法进行量化对比验证，因此有必要加强非线性因素对流激振动量化影响的研究。

［1］ 王春旭，吴崇健，陈乐佳，等.流致噪声机理及预报方法研究综述［J］.中国舰船研究，2016，11（1）：57-71. WANG C X，WU C J，CHEN L J，et al.A comprehen⁃sive review on the mechanism of flow-induced noise and related prediction methods［J］.Chinese Journal of Ship Research，2016，11（1）：57-71（in Chinese）.

［2］ 俞孟萨，吴有生，庞业珍.国外舰船水动力噪声研究进展概述［J］.船舶力学，2007，11（1）：152-158. YU M S，WU Y S，PANG Y Z.A review of progress for hydrodynamic noise of ships［J］.Journal of Ship Me⁃chanics，2007，11（1）：152-158（in Chinese）.

［3］ 白莱文斯R D.流体诱发振动［M］.吴恕三，译.北京：机械工业出版社，1983.

［4］ 伏欣H W.气动弹性力学原理［M］.沈克扬，译.上海：上海科学技术文献出版社，1982.

［5］ 道尔E H，小柯蒂斯H C，斯坎伦R H，等.气动弹性力学现代教程［M］.陈文俊，尹传家，译.北京：中国宇航出版社，1991.

［6］ TSIEN H S.The poincaré-lighthill-kuomethod［J］.Ad⁃vances in Applied Mechanics，1956，4：281-349.

［7］ 张效慈，司马灿，吴有生.潜艇舵低速颤振现象及其预报［J］.船舶力学，2001，5（1）：70-72. ZHANG X C，SIMA C，WU Y S.Low-speed flutter phenomenon of submarine rudder and its prediction［J］.Journal of Ship Mechanics，2001，5（1）：70-72（in Chinese）.

［8］ JEWELL D A，MCCORMICK M E.Hydroelastic in-stability of a control surface：DTMB-TR-1442［R］. Carderok，MD：David Taylor Model Basin，1961.

［9］ WRIGHT J R，COOPER J E.Introduction to aircraft aeroelasticity and loads［M］.New York：John Wiley& Sons Ltd，2008.

［10］ LIM C W，WU B S.A new analytical approach to the Duffing-harmonic oscillator［J］.Phys Lett：A，2003，311（4/5）：365-373.

［11］ 肖清，谢俊超，陈东阳.舵系统的颤振计算与分析［J］.中国舰船研究，2016，11（5）：48-54. XIAO Q，XIE J C，CHEN D Y.Flutter calculation and analysis of rudder system［J］.Chinese Journal of Ship Research，2016，11（5）：48-54（in Chinese）.

Theoretical and experimental research on influencing factors and rules of flow-induced rudder system vibration

XIAO Qing，HU Gangyi，XIE Junchao
China Ship Development and Design Center，Wuhan 430064，China

Flow-induced rudder system vibration has a great influence on the stealthiness of underwater vehicles.In order to study the vibration characteristics of rudder systems,a mathematical model of a binary linear flutter rudder system is built according to a simplified rudder system structure.Next,the conditions of low speed flutter of the rudder system are determined,and the main influence factors and control rules of the low speed flutter are obtained.In addition,flow-induced vibration tests of the rudder model are made in a gravitation water tunnel,and a study is made of the influences on the rudder system caused by variations in such main parameters as support stiffness,torsional stiffness,mass center position and stiffness center position.The results show that the structural design has a great influence on flow-induced rudder system vi⁃bration.The flow-induced vibration of the rudder system can be effectively suppressed through the match⁃ing design of such parameters as the frequency ratio of heave motion and torsion motion,the ratio of the structural mass and added mass,and the positions of the stiffness center,mass center and chord center.

rudder system；flow-induced vibration；low-speed flutter；water tunnel

U664.36

A

10.3969/j.issn.1673-3185.2017.01.013

2016-04-27

2016-12-28 15:39

国家部委基金资助项目

肖清（通信作者），男，1979年生，博士，高级工程师。研究方向：船舶装置。E-mail：xqzju98@163.com胡刚义，男，1966年生，博士，研究员，博士生导师。研究方向：船舶力学

http://www.cnki.net/kcms/detail/42.1755.TJ.20161228.1539.016.html期刊网址：www.ship-research.com

肖清，胡刚义，谢俊超.舵系统流激振动影响因素及规律的理论与试验研究［J］.中国舰船研究，2017，12（1）：84-92，100. XIAO Q，HU G Y，XIE J C.Theoretical and experimental research on influencing factors and rules of flow-induced rudder system vibration［J］.Chinese Journal of Ship Research，2017，12（1）：84-92，100.