三维水翼梢涡流场数值研究
2017-01-11蒲汲君熊鹰
蒲汲君,熊鹰
海军工程大学舰船工程系,湖北武汉430033
三维水翼梢涡流场数值研究
蒲汲君,熊鹰
海军工程大学舰船工程系,湖北武汉430033
针对三维水翼梢涡流场和梢涡空泡初生的问题,分别建立k-ω,DES和LES模型,对水翼的梢涡流场进行计算研究。为减少误差,在网格的处理上对梢涡流域进行局部加密,对未发生空化时梢涡内的轴向速度和切向速度进行计算,发现LES模型的计算结果与实验值吻合较好。在此基础上,讨论尾涡的卷曲对梢涡压力场的影响,提出了使用气泡静力平衡方程计算初始梢涡空泡数的方法。
梢涡;气泡静力平衡方程;空泡初生;水翼
0 引 言
自1859年Besant[1]的早期研究以来,梢涡空泡一直是学者们研究的焦点。当一个气核进入到涡核当中,如果这里的压力比临界压力更小,那么气核将会迅速长大并形成一个肉眼可见的空泡。空泡在溃灭过程中会释放强烈的辐射噪声并造成螺旋桨和船舵的剥蚀。空泡的类型包括梢涡空泡、片空泡、云空泡和游移型空化。大量实验发现,梢涡涡核中心处的局部压力最低,除了梢部有卸载处理的三维水翼和螺旋桨外,梢涡空泡在所有类型的空泡中最早出现(Keller[2]在其相关实验中已有发现),它产生的噪声会对舰船隐身性产生巨大影响。为抑制梢涡空泡的产生,很有必要准确计算出梢涡流域的流场特性。但是,由于梢涡本身的不稳定性,准确把握梢涡流场的特性还是一个较为困难的问题。解决该问题的有效途径是进行高精度的数值计算,它能提供梢涡流域流场的具体细节。
Fruman和Arndt等[3-4]对梢涡的流场分布进行了大量研究。与实验相比,数值计算的效率高、成本低,且更容易得到梢涡的流场分布细节。因此,使用数值方法计算梢涡流场越来越成为如今的主流方法。但值得注意的是,梢涡流场的速度梯度大,流场分布复杂。选取合适的湍流模型和对梢涡流场的网格进行细化处理是十分必要的。现在广泛运用的RANS方法对雷诺项进行了平均处理,只能得到时均化后的湍流结果,忽略了小尺度的湍流结构变化,使得RANS在模拟梢涡中效果很不理想[5]。在计算网格方面,Turnock等[6]提出了通过寻找压力最低点定位梢涡轨迹的方法,通过该方法极大地提高了计算精度。Zhang等[7]则认为数值计算中涡核径向网格节点数应大于15才能满足计算精度。
本文的计算模型是剖面为NACA 16020翼形的半椭圆形水翼,使用不同的湍流模型计算其流场分布,并与实验值做对比,以选取合适的湍流模型。在此基础上,使用气泡静力方程计算初始梢涡空泡数。
1 数值方法
1.1 RANS模型介绍
RANS模型是一种将流体的质量、动量等时均化处理的湍流模型[8]。雷诺平均方法不用求解各个尺度的湍流流动,只计算平均运动。当流体的湍流结构较为复杂时,RANS模型只能给出时均化后的结果。所以,对于复杂的流动现象,RANS模型是不适用的。
雷诺平均后的N-S方程如下所示:

式中:xi(i=1,2,3),xj(j=1,2,3),xl(l=1,2,3)为三维笛卡尔坐标系下的方向坐标;t为时间;ui,uj和ul为速度分量;ρ为流体密度;u为动力粘性系数;为雷诺应力;fi为体积力;
1.2 LES模型介绍
湍流流动中包含着各种尺度的湍流结构,大尺度涡主要指尺寸大于平均流动(注:剪切层厚度)的湍流结构。与大尺度涡相比,小尺度涡主要起耗散湍流能量的作用。基于该基本现象,LES使用直接数值求解的方法计算大尺度涡,建立模型求解小尺度涡。模型中分离大、小尺度涡的分界尺度称为过滤尺度,用Δ表示。它相较于普通的RANS模型,要求更细致的网格分布和更多的计算资源[9]。
LES的控制方程如下所示:
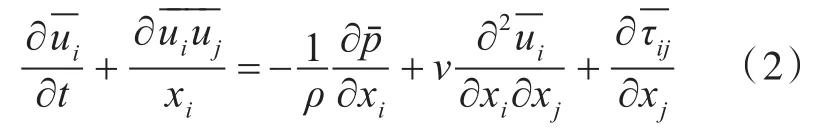

式中:Lij为Leonard应力,代表着大尺度涡之间的相互作用;Cij为交互应力,代表着大尺度涡和小尺度涡之间的相互作用;Rij为亚网格雷诺应力,代表着小尺度涡之间的相互作用[10]。Lij,Cij和Rij分别表示如下:

1.3 DES模型介绍
DES模型是一种介于RANS和LES之间的湍流模型,它在边界层内使用RANS模型,其他区域使用LES模型,所占的计算资源比RANS模型多,但比LES模型少。本文研究的DES为基于k-ω的湍流模型。
该DES模型与k-ω模型相比,对耗散项Yk提出了如下修正:

2 计算模型和网格划分
本文的计算模型是剖面为NACA 16020翼形的半椭圆形水翼,实验[3]已在空泡水洞中完成,来流速度为10 m/s,翼攻角为10°。入口距离水翼3倍弦长,设置为速度入口;出口距离水翼10倍弦长,设置为压力出口。其中,原点设置在水翼根部中心位置。所建计算域如图1所示。
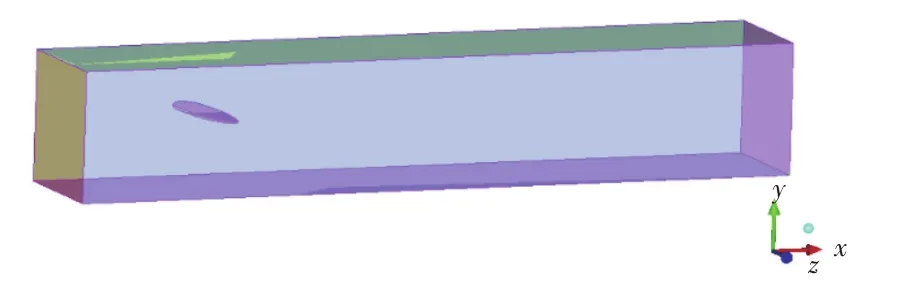
图1 计算域Fig.1 Computational domain
根据计算域的几何形状,本文主要用H型网格对计算域进行整体网格划分。考虑到梢涡的形成与翼边界层内流动有关,为较准确地模拟边界层内流场,本文应用O型网格对翼壁面附近的网格进行了处理,以提高网格质量,第1层网格尺度y+在1~30之间。为与实验结果相对比,本文建立的计算域与实验一致。本文分别建立了2个坐标系,其中绝对坐标系的原点设在水翼底部弦长中心处,x,y,z的方向如图1所示。为便于对梢涡进行分析,本文还建立了相对坐标系,其原点位于各个界面处梢涡涡核的中心,x,y,z的方向与绝对坐标系相同。在没有明确指出时,默认为绝对坐标系。
根据Turnock等[6]提供的方法:通过初步计算得到尾流区域每个截面压力最低点的位置,可以认为这些点的连线即是梢涡轨迹,并对该连线进行径向和轴向的网格加密,得到优化网格。同时,Dehghan等[8]也指出,在数值计算中,涡核径向网格节点数应大于15才能满足计算精度。划分涡核内网格节点为20×20,总网格数为800万。
3 梢涡流场数值研究
三维水翼梢涡处流场结构复杂,主涡和二次涡的相互干扰影响为数值模拟带来了相当的难度,同时,梢涡的能量耗散问题也给湍流模型的使用造成了困难。在应用不同的湍流模型时,轴向速度与实验值相比,存在着较大的不同。Spalart等[11]指出,经过旋转和曲率修正的湍流模型能够有效抑制涡核处的粘性耗散,从而提高计算精度。但经计算发现,曲率修正后的湍流模型会反向减小梢涡处的轴向速度,使其与实验值相差更大。图2和图3给出了x方向3个位置处梢涡流场无因次轴向速度(U/U∞)和切向速度(Vt/U∞)沿y轴分布的计算结果与实验结果。其中,轴向是指与梢涡涡线平行的方向,切向为与梢涡涡线垂直的方向,由于梢涡轨迹近似于x轴方向(来流方向)平行,这里认为轴向速度为x方向速度,切向速度为z方向速度。



图2 梢涡轴向速度分布图Fig.2 Profiles of axial velocity in tip vortex
由图2可知,k-ω模型和基于k-ω的DES模型在预报梢涡轴向速度方面存在较大误差,特别是涡核处的速度分布,与实验值截然相反。这可能是由于这两个模型都过大地预报了梢涡处的粘性耗散,使得速度下降得过快。而使用曲率修正后的湍流模型则更加大了粘性耗散,这明显与文献[10]的结论相异,可能的原因是曲率修正的使用建立在一些先决条件上,否则会得到相反的结论,对曲率修正的研究会在以后的工作中继续展开。LES湍流模型则给出了较好的预报结果,特别是x/C=0.1处涡核的速度分布与实验吻合很好。而在梢涡空泡观测中,发现梢涡空泡的初生位置一般在x/C=0.1附近。所以对该位置速度流场的准确模拟为下一步研究梢涡空泡的初生打下了良好的基础。


图3 梢涡切向速度分布图Fig.3 Profiles of tangential velocity in tip vortex
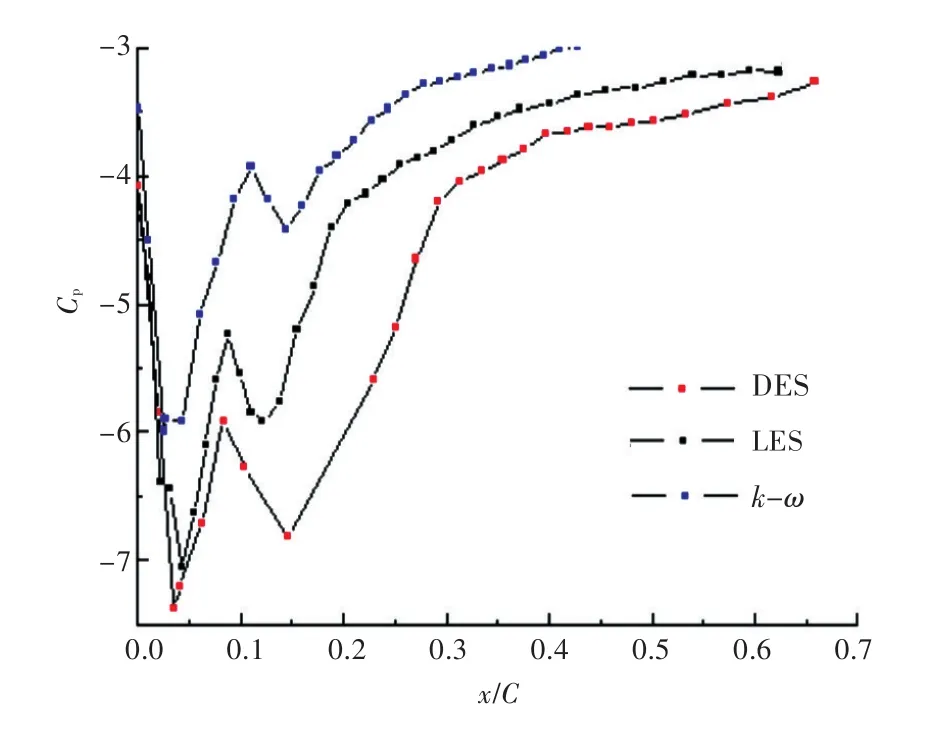
图4 梢涡轨迹方向最小压力系数分布Fig.4 Pressure coefficients along the tip vortex trajectory
由图3可知,各湍流模型对梢涡切向速度分布的预报效果均较好,特别是LES模型在x/C=0.3处梢涡粘性出现较大耗散的情况下也能与实验值符合较好。但在局部坐标z<0的区域,各湍流模型预报的结果都与实验值存在较小的误差,这可能是由于三维水翼壁面对主涡的干扰所致。图4给出了沿x方向涡核处的最低压力系数分布(Cp),LES,DES和RANS模型的最小压力都出现在x/C= 0.355 5处,对应的最小压力系数分别为-7.38,-7.05和-5.98。很明显,RANS湍流模型过高地预报了粘性耗散,使最小压力系数与LES和DES的预报结果差距较大。从图4可以明显看出,LES和DES湍流模型给出的最低压力系数曲线存在一个较为明显的二次降低区域。该区域的存在是由于主涡沿梢涡轨迹方向行进时,会将水翼产生的其他尾涡卷曲进来,当两涡螺旋式缠绕并合并时,会增大主涡的涡强,从而使涡核内流速增大,压强降低;与此同时,在主涡的行进过程中又会不断地耗散能量,所以存在一个相对平衡的点,使主涡的耗散能量和卷曲获得的能量相等。
4 气泡静力平衡和初始梢涡空泡数计算
描述微气泡体积变化的经典Rayleigh-Plesset方程为

等式左边为动态项,代表了气泡体积的变化;右边为静态项,仅与气泡的受力情况有关。当气泡体积变化较为缓慢时,可忽略方程左边的动态项,方程简化为研究空泡初生时的静力平衡方程
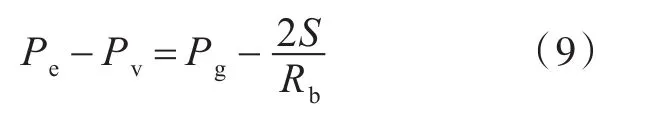
式(8)和式(9)中:Pe为气泡周围的环境压力,当气泡的体积很小时,Pe通常取气泡中心点的压力;Pv为饱和蒸汽压;Pg为气泡中的气体压力;Rb为气泡半径;S为气泡表面的张力系数;R0为气泡初始半径;v为运动粘性系数;pv和pencoutner为气泡周围压力;U为流体速度;Ub为气泡速度;pg0为初始气泡内气体压力。
当气泡周围的环境压力变化时,气泡的半径会根据其平衡状态随之改变。由于发生空化时液体气化的速度非常快,设定气泡中蒸汽压力恒为常数。另一方面,水中气体扩散的速度相较于空化的速度来说十分缓慢,所以可以假设气泡中气体的质量恒为常数。因此Pg的表达式为

最终的气泡平衡方程为
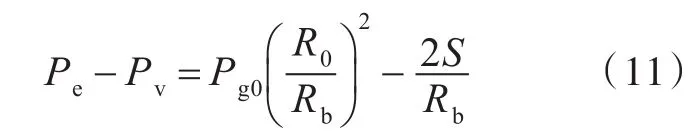
其中,

图5给出了球型气泡的静力平衡曲线[12],其中Critical values为临界边界线,该边界线以下的区域属于非平衡区域,处于该区域的气泡会迅速长大。因此,由边界线与静力平衡曲线的交点即可确定临界压力与临界半径。

图5 气泡静力平衡曲线[12]Fig.5 Static equilibrium curves of bubbles[12]
求得的临界压力Pc与临界半径Rc如下所示:

当流场压力小于临界压力Pc时,气泡会迅速长大,梢涡空泡随之产生。当使用气泡平衡方程时,不仅要考虑流场环境,还需要考虑气核的初始半径。这里分别设定气泡的初始半径R0=30,50,100 μm,Pv=3 540 Pa,研究不同初始半径下的梢涡空泡数。
已知三维水翼的最小压力系数为-7.38(使用LES模型计算的结果),当梢涡空泡初生时,Pe=Pc。联立式(13)和式(14),可计算出Rc,Pc和初生空泡数δi,计算结果如表1所示。

表1 三维水翼初始梢涡空泡计算结果Table 1 The computational results of hydrofoil vortex cavitation inception
从以上计算结果可以看出,不同初始半径下临界压力相差较大,导致各个不同初始半径的初始梢涡空泡数相差很大。从以上结果还可以发现,临界压力总是小于汽化压力,所以当对控制梢涡空泡初生要求较高时,可使用偏于安全的汽化压力来计算初始梢涡空泡数。但在需要对初始梢涡空泡数进行精确计算时,则必须使用临界压力来计算梢涡空泡数。
使用气泡静力方程能准确计算出初始梢涡空泡数,该方法为后续初始梢涡空泡数的尺度效应研究奠定了基础。
5 结 论
本文应用k-ω,DES和LES模型分别计算了翼剖面为NACA 16020翼型的椭圆形水翼梢涡流场分布,介绍了气泡静力平衡方程,并结合气泡静力平衡方程研究了该水翼的初始梢涡空泡,得到以下结论:
1)RANS湍流模型过大地预报了梢涡的粘性耗散,在应用曲率修正以后,结果并没有得到改善,反而反向减小了轴向速度,这与文献[10]的结论相悖。使用LES湍流模型则能够得到较好的结果。
2)应用LES湍流模型能准确预报出由于尾涡的卷曲合并对梢涡处压力场的影响,为后续的梢涡空泡研究奠定了基础。
3)在使用气泡静力平衡方程预报初始梢涡空泡数的情况下,当对控制梢涡空泡初生的要求较高时,可使用偏于安全的汽化压力来计算初始梢涡空泡数。在需要对初始梢涡空泡数进行精确计算时,必须使用临界压力计算梢涡空泡数。
[1] BESANT W H.A treatise on hydrostatics and hydrody⁃namics[M].London:Deighton,Bell,1859.
[2] KELLER A P.Cavitation scale effects-empirically found relations and the correlation of cavitation number and hydrodynamic coefficients[C]//CAV 2001:Fourth International Symposium on Cavitation.Pasadena,CA,USA:California Institute of Technology,2001.
[3] FRUMAN D H,DUGUÉ C,PAUCHET A,et al.Tip vortex roll-up and cavitation[C]//Proceedings of the 19th Symposium on Naval Hydrodynamics.Washing⁃ton D C,USA:National Academy,1992:633-654.
[4] ARNDT R E A,ARAKERI V H,HIGUCHI H.Some observations of tip-vortex cavitation[J].Journal of Flu⁃id Mechanics,1991,229:269-289.
[5] 吴琼,叶骞,孟国香.不同湍流模型在旋流非接触搬运器仿真中的应用和对比[J].上海交通大学学报,2013,47(3):423-427. WU Q,YE Q,MENG G X.Application and compari⁃son of the different turbulent models simulation for non-contact vortex gripper[J].Journal of Shanghai Ji⁃aotong University,2013,47(3):423-427(in Chi⁃nese).
[6] TURNOCK S R,PASHIAS C,ROGERS E.Flow fea⁃ture identification for capture of propeller tip vortex evolution[C]//Proceedings of the 26th Symposium on Naval Hydrodynamics.Rome,Italy:Italian Ship Mod⁃el Basin,Office of Naval Research,2006.
[7] ZHANG L X,ZHANG N,PENG X X,et al.A review of studies of mechanism and prediction of tip vortex cavitation inception[J].Journal of Hydrodynamics:Ser.B,2015,27(4):488-495.
[8] DEHGHAN M,TABRIZI H B.Turbulence effects on the granular model of particle motion in a boundary lay⁃er flow[J].The Canadian Journal of Chemical Engi⁃neering,2014,92(1):189-195.
[9] 甘文彪,周洲,许晓平,等.基于改进SST模型的分离流动数值模拟[J].推进技术,2013,34(5):595-602. GAN W B,ZHOU Z,XU X P,et al.Investigation on improving the capability of predicting separation in modified SST turbulence model[J].Journal of Propul⁃sion Technology,2013,34(5):595-602(in Chi⁃nese).
[10] MORGUT M,NOBILE E,BILUŠ I.Comparison of mass transfer models for the numerical prediction of sheet cavitation around a hydrofoil[J].International Journal of Multiphase Flow,2011,37(6):620-626.
[11] SPALART P R,SHUR M.On the sensitization of tur⁃bulence models to rotation and curvature[J].Aero⁃space Science and Technology,1997,5(1):297-302.
[12] CHAHINE G L.Nuclei effects on cavitation inception and noise[C]//Proceedings of the 25th Symposium on Naval Hydrodynamics.St.John's,Newfoundland and Labrador,Canada:[s.n.],2004.
Numerical study of hydrofoil tip vortex fluid field
PU Jijun,XIONG Ying
Department of Naval Architecture Engineering,Naval University of Engineering,Wuhan 430033,China
Three different models,k-ω,DES and LES,are conducted in the analysis of the tip vortex flow field.In order to reduce the discrete error induced by the grid,mesh refinement is applied to the area of the tip vortex core in numerical simulations.The axis and tangential velocities of the tip vortex flow field with no cavitation are calculated,and the calculated velocities agree well with the experimental results.On the basis of this process,the influence of vortex roll-up on the tip vortex pressure filed is discussed,and bubble static equilibrium is proposed by which the tip vortex cavitation inception number is computed.
tip vortex;bubble static equilibrium;cavitation inception;hydrofoil
U661.313
A
10.3969/j.issn.1673-3185.2017.01.002
2016-06-03
2016-12-28 16:05
国家自然科学基金资助项目(51179198)
蒲汲君,男,1991年生,硕士生。研究方向:流体力学。E-mail:211982361@qq.com熊鹰(通信作者),男,1958年生,博士,教授,博士生导师。研究方向:船舶流体力学。E-mail:ying_xiong28@126.com
http://www.cnki.net/kcms/detail/42.1755.TJ.20161228.1605.038.html期刊网址:www.ship-research.com
蒲汲君,熊鹰.三维水翼梢涡流场数值研究[J].中国舰船研究,2017,12(1):8-13,26. PU J J,XIONG Y.Numerical study of hydrofoil tip vortex fluid field[J].Chinese Journal of Ship Research,2017,12(1):8-13,26.
