新型线性自抗扰控制器在船舶动力定位控制系统中的应用
2017-01-11金月俞孟蕻袁伟
金月,俞孟蕻,袁伟
江苏科技大学电子信息学院,江苏镇江212003
新型线性自抗扰控制器在船舶动力定位控制系统中的应用
金月,俞孟蕻,袁伟
江苏科技大学电子信息学院,江苏镇江212003
针对船舶在海上作业时动力定位控制系统需要精准定位的问题,提出基于改进跟踪微分器的自抗扰控制器,解决线性自抗扰控制器由于省略跟踪微分器而降低系统动态性能的问题。结合线性与非线性跟踪微分器的优点,设计能够较好跟踪微分信号,且能降低噪声对系统影响的改进跟踪微分器,从而构成新型线性自抗扰控制器。仿真实验结果表明,相比于传统的线性自抗扰控制器,基于改进跟踪微分器的LADRC有较强的鲁棒性和自适应性,且超调小、响应快、抗扰能力强。
船舶动力定位控制;线性自抗扰控制;改进跟踪微分器
0 引言
随着海洋事业的不断发展,人们对海洋的开发和探索逐渐向深海扩展,在海洋工程设施建设中,船舶海上作业已经成为了不可或缺的重要部分。由于海洋环境的复杂性,对船舶动力定位系统的精度越来越严苛。为了增强系统的鲁棒性,近几年提出了一些控制方法,包括:线性反馈控制、La Salle不变集控制、Laypunov指数控制、自适应控制和有限时间控制等。这些现代控制对被控对象的精确模型依赖非常大,在使用现代控制理论进行控制时大多使用的是简化模型或者假设的系统模型,适应性和鲁棒性不好。自抗扰控制(Active Disturbance Rejection Control,ADRC)是近年由韩京清[1]在非线性PID的基础上提出的新型非线性控制算法,抗干扰能力强且不依赖于控制对象的精确模型,解决了现代控制存在的问题。岳华[2]将ADRC应用至船舶动力定位的控制系统中,利用跟踪微分器来安排过渡过程,其虽然化解了超调量与响应速度之间的矛盾,但是实现的过程较为复杂,参数整定过程较为繁琐。基于ADRC的思想,Gao[3]提出了线性自抗扰控制器(LinearActive Disturbance Rejection Control,LADRC),为了减少需要调节的参数,直接省略ADRC中的非线性跟踪微分器,因此,在PD控制器中没有引入参考输入的微分项,该方法降低了系统的动态性能。近年来,也有许多学者提出了一些改进的非线性跟踪微分器[4-5],如高增益跟踪微分器所需整定的参数较少,并且动态响应速度快,跟踪精度高,但是不足之处在于参考输入受到污染时,其噪声的放大作用明显。传统的线性跟踪微分器[5]虽然能够实现稳态无差,但相比于非线性跟踪微分器,动态响应明显较慢。
基于上述情况,本文将设计结合线性与非线性优点的跟踪微分器,构成新型自抗扰控制器,将其应用至船舶动力定位控制系统中,并进行仿真实验。
1 船舶动力定位数学模型
在船舶动力定位系统研究过程中,一般只考虑3个自由度,即横荡、纵荡和艏摇。同时,系统建模一般还需要2个坐标系,一个是相对地球固定的大地坐标系xeoeye;另一个是相对船舶建立的船体坐标系xoy[6-8],如图1所示。
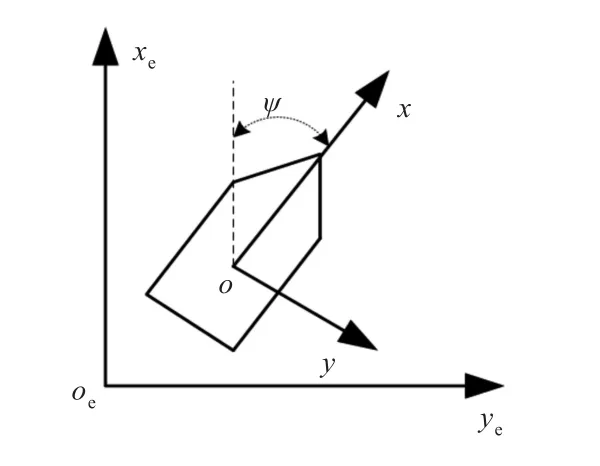
图1 大地坐标系和船体坐标系Fig.1 The earth coordinate system and body coordinate system
其中,船舶运动学模型和低频动力学模型为

式中:ξ是6维列向量;η是船舶纵荡、横荡及艏摇方向的低频运动矢量;R(ψ)为两坐标系之间的转换矩阵;Tb是包含时间常数的对角矩阵;b是纵荡、横荡、艏摇3个自由度上的力和力矩;Eb是环境扰动力和力矩的幅值;ωb是均值为0的高斯白噪声向量;M为质量矩阵;D称为阻尼系数矩阵;ν=[u,υ,r]T,为船舶在船体坐标系下的横荡、纵荡和艏摇角速度;τ为推进系统的力和力矩;Ch=[03×3I3×3],I是单位矩阵。

式中:ω0为谱峰频率;m是船舶总质量;xg是船舶中心和重心之间的距离,一般取xg≈0;Iz是转动惯性矩阵;Xu,Yυ,Yr,Nυ,Nr均是水动力系数;Xu̇,Yυ̇,Nṙ,Yṙ,Nυ̇均是附加质量系数。
2 线性自抗扰控制器
LADRC[9]技术,通过线性扩张状态观测器(LESO)来估计出系统的总扰动,并进行动态反馈补偿,将系统简化为积分串联标准型,获取一阶微分信号,在此基础上,利用PD控制设计合理简单的控制率。
设二阶系统为

式中:f=-aẏ-dy+w+(d-b0)u为系统不确定的总扰动;y为输出;u为输入;w为外界的扰动。参数a,d为变量参数,b0≈d,式(2)的状态方程形式为

式中:x1,x2为二阶系统的状态变量;x3=f为系统加入的增广状态;̇为未知扰动。可通过状态空间模型的状态观测器估计出f的值,模型为

其中:

该状态观测器定义为LESO,则式(4)可改写为
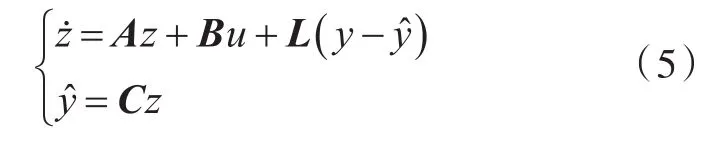

取控制律为

忽略估计误差z3和不确定总扰动f,系统可简化为一个双积分串联结构

上式可改写成PD控制
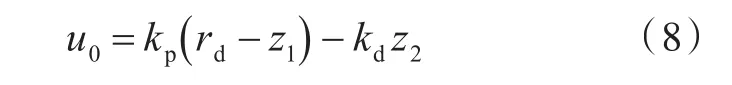
式中,rd为给定量,且-kdz2的存在使系统的闭环传递函数成为一个不包含零点的纯二阶传递函数

其中,s为复变量。控制器增益可选为:

式中:ωc和χ分别是期望闭环系统的固有频率和阻尼比;χ用于避免系统出现振荡。
由于不依赖于被控对象的精确模型,因此线性自抗扰控制技术控制效果好且使用范围广。但针对船舶在动力定位过程中受到海洋环境扰动的影响比较大且对定位精度要求高的情况,LADRC在动态特性方面还有进一步提高的空间。
3 基于新型LADRC的船舶动力定位控制器设计
3.1 改进跟踪微分器的设计
微分环节的一般形式为
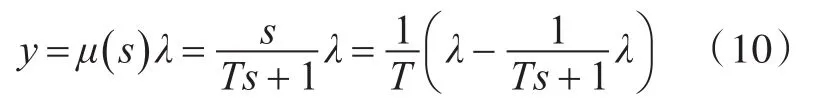
式中:T为时间常数;μ(s)为微分环节;λ为输入信号的直接输出。设表示一个以T为时间常数的惯性环节,则其时域形式为
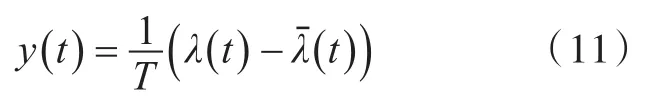

代入式(11)中,可得
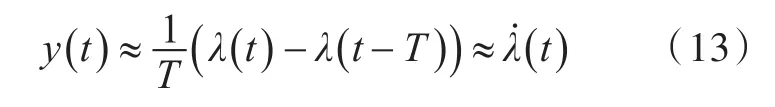
从式(13)的推导可知,当采样时间常数T取值越小,输出值就和微分值越接近,而且,延迟信号就与越接近,增大了微分的还原程度。但是,一旦噪声信号污染了输入信号,则噪声经过微分环节之后会被放大。
对上式中微分的近似形式进行改进以消除噪声放大效应的影响,表示为


3.2 控制器的设计
在船舶动力定位系统中,一般只考虑船舶水平面运动,即横荡、纵荡、艏摇,且不考虑该3个自由度的耦合情况,假设3个方向的运动是相互独立的,故需要在3个自由度上分别设计3个独立的自抗扰控制器。控制系统框图如图2所示,控制器的输入为船舶的期望位置和船舶的实际位置,输出为控制指令。图2中,v为状态输入;e1,e2为误差;z1为状态输入的观测值,z2是z1的近似微分,z3为观测误差;v1,v2为经过改进跟踪微分器后的状态输入。

图2 新型线性自抗扰控制器结构图Fig.2 Structure diagram of novel LADRC
将船舶的数学模型转换成与自抗扰控制理论相对应的形式
问题:(1)用一张正方形的纸怎样才能制成一个无盖的长方体形盒子?( 假设这张正方形纸的边长a为20 cm,所折无盖长方体形盒子的高为h cm)
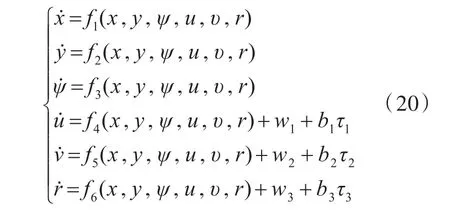
式中:fi(x,y,ψ,u,υ,r)(i=1,2,…,6)是系统的内部扰动;wi(i=1,2,3)是外部扰动;τi(i=1,2,3)是控制力;bi(i=1,2,3)为系数。
基于改进跟踪微分器的线性自抗扰控制器是由改进跟踪微分器、线性扩张观测器和PD控制构成的。由于3个独立的控制器设计方法相同,故以纵荡控制器设计为例说明,纵荡方向的公式

式中:x为纵荡位置;u为纵荡速度;w1为外界扰动;τ1为纵荡控制力。
具体算法如下:
改进线性跟踪微分器

4 仿真对比分析
现以某船舶[10]为仿真对象,利用Matlab2013b软件来验证LADRC和基于改进跟踪微分器的LADRC(TD-LADRC)在船舶动力定位系统中的性能,该船舶相关参数如表1所示。

表1 仿真试验的主要参数Table 1 The main parameters of the simulation experiment
其中,船舶模型的质量矩阵和阻尼系数矩阵分别为:

TD-LADRC纵向控制器参数为:ω1=0.08,ωc1=0.8,b1=1,λ1=1;
TD-LADRC横向控制器参数为:ω2=0.08,ωc2=0.8,b2=1,λ2=1
TD-LADRC艏向控制器参数为:ω3=1 000,ωc3=10,b3=1,λ3=1
图3为在海洋环境干扰力较小的情况下船舶在纵荡、横荡、艏摇三方向的位置输出,图4为小环境干扰力下船舶的运动轨迹。假设仿真海洋环境[10]为:风速为5 m/s,风向角为30°,浪向为30°,流向为150°,有义波高为0.5 m,流速为0.2 m/s。通过响应曲线可以得出:由于系统加入了小海况干扰,LADRC控制器控制船舶3个方向位置的输出已经出现了振荡,而TD-LADRC控制曲线在一开始波动比较大,但在100 s左右开始进入稳态逐渐平缓。

图3 小干扰情况下位置输出Fig.3 Position output in small interference
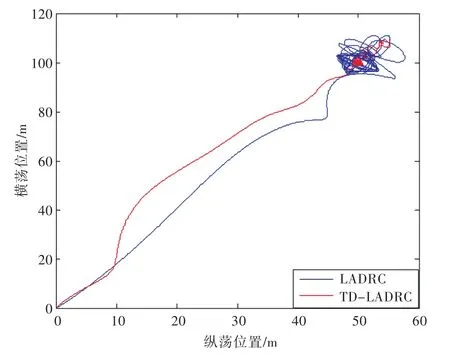
图4 小干扰情况下船舶的运动轨迹Fig.4 Ship motion trajectory in small interference
图5为在较大海洋环境干扰力的情况下,船舶在纵荡、横荡、艏摇三方向的位置输出,图6为大环境干扰力下船舶的运动轨迹。假设仿真海洋环境[10]为:风速为15 m/s,风向角为30°,浪向为30°,流向为150°,有义波高为3 m,流速为2 m/s。通过响应曲线可以得出:在有较大海况干扰的条件下,LADRC的控制曲线出现了较大的振荡,从图6船舶的运动轨迹更可以看出船舶基本已经失控,而TD-LADRC不仅波动幅值小,很快达到稳定,响应速度也比LADRC的快,船舶也能很平稳地到达定位点,说明其抗扰能力强。其实,即使增大仿真的环境干扰力,TD-LADRC也具有良好的控制效果。
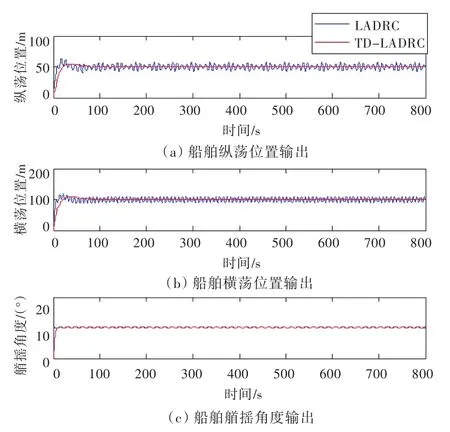
图5 大干扰情况下位置输出Fig.5 Position output in big interference

图6 大干扰情况下船舶的运动轨迹Fig.6 Ship motion trajectory in big interference
由图3~图6可以看出:由LADRC和改进LADRC所控制的起重船在横荡、纵荡、艏摇这3个方向的位置输出,在控制器的参数和船舶对象模型的参数不变,而外界环境的干扰力发生变化的情况下,改进后的控制器能逐渐保持在给定的期望值上,所受到的影响较小,故基于改进跟踪微分器的LADRC有较强的鲁棒性和自适应性。
5 结 语
针对船舶海上作业时动力定位控制系统需要精准定位的问题,本文结合线性和非线性跟踪微分器的优点,提出了一个改进的跟踪微分器,能快速、准确地提供参考输入的跟踪信号及微分信号,构成新型自抗扰控制器。通过定点仿真实验,在改进LADRC控制下的纵荡、横荡和艏摇都能逐渐保持在给定的期望值上,且超调小、响应快、抗扰能力强,证明了基于改进跟踪微分器的线性自抗扰控制器在起重船动力定位中的有效性。实验结果表明,在不同环境干扰力的情况下,新型线性自抗扰控制器有较强的鲁棒性和自适应性,且动态性能好,可作为船舶动力定位控制系统的一种新选择。
[1] 韩京清. 自抗扰控制技术——估计补偿不确定因素的控制技术[M]. 北京:国防工业出版社,2008.HAN J Q. Active disturbance rejection controltechnique-the technique for estimating and compensatingthe uncertainties [M]. Beijing: National DefenseIndustry Press,2008(in Chinese).
[2] 岳华.基于自抗扰的船舶动力定位控制方法研究[D].哈尔滨:哈尔滨工程大学,2012. YUE H.Research on dynamic positioning control method of a vessel based on auto disturban rejection controller[D]. Harbin: Harbin Engineering University,2012(in Chinese).
[3] GAO Z Q.Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the American Control Conference.Denver,CO,USA:IEEE,2003:4989-4996.
[4] 谢云德,龙志强.高精度快速非线性离散跟踪微分器[J].控制理论与应用,2009,26(2):127-132. XIE Y D,LONG Z Q.A high-speed nonlinear discrete tracking-differentiator with high precision[J].Control Theory&Applications,2009,26(2):127-132(in Chinese).
[5] 史永丽,侯朝桢.改进的非线性跟踪微分器设计[J].控制与决策,2008,23(6):647-650,659. SHI Y L,HOU C Z.Design of improved nonlinear tracking differentiator[J].Control and Decision,2008,23(6):647-650,659(in Chinese).
[6] 王庆林,姜增如,刘喜梅.线性跟踪微分器及其在状态反馈控制中的应用[J].北京理工大学学报,1999,19(2):203-206. WANG Q L,JIANG Z R,LIU X M.Linear tracking differentiators and its applications in state feedback control[J].Journal of Beijing Institute of Technology,1999,19(2):203-206(in Chinese).
[7] 贾欣乐,杨盐生.船舶运动数学模型[M].大连:大连海事大学出版社,1999. JIA X L,YANG Y S.Ship motion mathematical model[M].Dalian:Dalian Maritime University Press,1999(in Chinese).
[8] 边信黔,付明玉,王元慧.船舶动力定位[M].北京:科学出版社,2011. BIAN X Q,FU M Y,WANG Y H.Ship dynamic positioning[M].Beijing:Science Press,2011(in Chinese).
[9] 奚庆潮.船舶航向自抗扰控制的研究[D].大连:大连海事大学,2014. XI Q C.Research on ship course control based on the ADRC[D].Dalian:Dalian Maritime University,2014(in Chinese).
[10] 高峰.船舶动力定位自抗扰控制及仿真的研究[D].大连:大连海事大学,2013. GAO F.Research and simulation for ship dynamic positioning based on the ADRC[D].Dalian:Dalian Maritime University,2013(in Chinese).
Application of novel linear active disturbance rejection control in dynamic positioning control system of vessels
JIN Yue,YU Menghong,YUAN Wei
School of Electronic and Information,Jiangsu University of Science and Technology,Zhenjiang 212003,China
Aiming at the problem in which a vessel's dynamic positioning system can control it at an expected position,a novel linear active disturbance rejection controller is designed to solve the problem of poor dynamic performance due to the omission of a tracking differentiator.Based on the advantages of linear and nonlinear tracking differentiators,an improved tracking differentiator is designed which can track the differential signal and degrade the effects of noise;it constitutes a novel Linear Active Disturbance Rejection Controller(LADRC).The simulation results show that the novel LADRC based on the improved tracking differentiator has strong robustness,high control accuracy and good dynamic performance compared with the traditional LADRC.
vessel dynamic positioning control;linear active disturbance rejection controller;improved tracking differentiator
U664.82
A
10.3969/j.issn.1673-3185.2017.01.020
2016-05-04
2016-12-28 15:22
江苏省产学研联合创新资金资助项目(BY2013066-08);江苏高校高技术船舶协同创新中心/江苏科技大学海洋装备研究院资助项目(HZ2015006);江苏省科技支撑计划(工业)资助项目(BE2011149);江苏高校优势学科建设工程资助项目
金月,女,1992年生,硕士生。研究方向:船舶运动控制技术。E-mail:Blanche_Yueyue@163.com俞孟蕻(通信作者),男,1962年生,教授。研究方向:船舶综合控制技术。E-mail:Ymhzj2691@163.com
http://www.cnki.net/kcms/detail/42.1755.TJ.20161228.1522.002.html期刊网址:www.ship-research.com
金月,俞孟蕻,袁伟.新型线性自抗扰控制器在船舶动力定位控制系统中的应用[J].中国舰船研究,2017,12(1):134-139. JIN Y,YU M H,YUAN W.Application of novel linear active disturbance rejection control in dynamic positioning control system of vessels[J].Chinese Journal of Ship Research,2017,12(1):134-139.
