基于合规运输的第三方整车物流多式联运网络优化

刘弘超

内容摘要：公路运输过程中所产生的高额的过路过桥费与超载罚款成本是制约第三方整车物流企业发展的关键因素，与此同时，《GB1589-2016》和《车辆运输车治理方案》等治超法规的陆续出台，无疑使第三方整车物流企业降本增效难上加难。本文通过借鉴混合轴辐式理论，建立整车物流多式联运网络优化模型，设计适用于模型求解的禁忌算法，最后以第三方整车物流企业为例对模型进行仿真与分析。结果表明，相较于直通式物流网络，基于混合轴辐式理论的整车物流多式联运网络总成本将降低20%，运输方式趋于多元化，网络更具有竞争力。

关键词：整车物流 多式联运 混合轴辐式理论 网络优化

引言

2016年8月，交通部、发改委等部门联合发布《车辆运输车治理方案》，该《方案》提出2016年9月21日起严禁“双排车”进入高速公路，并督促汽车整车物流企业更新改造不合规运输车，到2018年7月1日起全面禁止不合规运输车通行。《方案》的实施对整个整车物流行业产生了极大影响，最直接的影响就是整车物流企业运营成本的上升。长期以来，我国的整车物流成本因运输方式单一、资源分散、企业各自为政、物流网络信息化程度低等原因而居高不下。新的治超政策实施后，整车公路运输成本因运输车辆装载量骤减而上升，再加之原有运输车辆的改造与新标准车型的购置，对整车物流企业降本无疑是雪上加霜。为了降低单一公路运输模式下的运营风险，规避新法规对商品车公路运输方式带来的影响，如何采用多元化的运输方式，提高铁路和水路运输的发运比例，已成为第三方整车物流企业的关注重点。

综合国内外研究情况，众多学者关于整车物流的理论研究集中体现在整车物流配送问题，主要包括整车路径优化（vehicle routing problem，VRP）和整车配载优化（vehicle loading problem，VLP）。例如，Roberto Baldacci（2011）等人运用精确算法求解有容量限制与带时间窗的车辆路径问题。Lee（2006）等将动态规划的理论运用于车辆路径问题的研究中，并运用最短路径算法求解。国内侯玉梅（2015）、王书勤等（2011）分别对具有时间约束与容量约束的车辆路径问题进行了研究，并运用不同的启发式算法进行求解。与此同时，钱丹等（2015）根据现代承运车的多层多排的结构特点，以单层、单排为粒度的可配载逻辑，构建了多承运车型联运的整车物流配送优化模型，并给出基于改进分支定界的新启发式配载优化算法。除以上研究外，陈建岭等（2015）将聚类分析与数学规划方法相结合，并运用米歇尔选址方法，提出一种综合性的选址方法来确定区域配送中心最佳的选址方案。赵欣（2014）以供应链竞争环境为背景，提出通过战略联盟、构建整车物流综合运输体系、搭建整车物流信息平台等方式进行资源整合，最终提升整车物流企业的核心竞争力。陈蔚（2011）在阐述商品车整车物流发展现状的基础上，分析铁路运输在商品车整车物流中的优势和存在的问题，并提出相关建议。

综上所述，虽然国内外学者对整车物流的研究范围不断扩大，但缺乏对整车物流运输网络的战略性规划，尤其是对枢纽节点选址布局、综合运输体系下的多种运输方式组合与车辆路径选择相结合的集成性研究少之又少，需进一步深入研究。因此，本文针对合规运输下商品车公路运输经济性较差、发运结构不合理等问题，在多式联运发展与研究应用的基础上，进一步引入轴辐式理论建立整车物流多式联运网络模型，构造禁忌算法进行求解，并结合实例对模型进行分析。

问题的提出

某第三方整车物流企业承担A汽车品牌的一批商品车运输任务，需从该汽车品牌的一个主机厂将生产的商品车分别发运至其下的M个4S销售中心。该第三方整车物流企业拥有一个整车分拨中心（VDC）服务于该汽车品牌，分布在该汽车品牌主机厂附近。由于受制于高额的公路运输成本与专项治超法规的约束，以及A汽车品牌运输需求的不断扩大，现需要该第三方整车物流企业打破传统的单一运输模式，布局p个区域整车配送中心（RDC），构建高效的商品车运输网络，开展多式联运服务，如图1所示。在不考虑商品车提前到达4S销售中心的存储成本或延迟到达的惩罚成本的情况下，确定所需建立p个RDC所在城市的集合，整个运输过程中城市间最佳的运输方式和运输路径组合，实现整个运输网络的成本最优。

整车物流多式联运网络优化模型构建

一个完整的整车物流多式联运网络中应该包含两种运输交换模式：一种是基于枢纽间接驳的联合运输，另一种则是起讫点之间的直接运输。在混合轴辐式理论中，运输网络中不仅存在“非枢纽点-枢纽点-非枢纽点”的连线，而且包含非枢纽节点间的连线，与上述整车物流多式联运网络特征符合。因此，本文主要是基于混合轴辐式理论对整车物流多式联运网络进行建模。

（一）混合轴辐式理论概述

O'kelly（1987）首先提出轴辐式网络枢纽选址模型，为轴辐式网络应用奠定了理论基础。自此之后，随着学者对轴辐式理论研究的不断深入与完善，这种典型高效的物流网络结构开始在航空运输、农产品、邮政快递、零担物流等领域广泛应用。

根据非枢纽节点之间是否存在直接连接，轴辐式网络可以分为纯轴辐式网络和混合轴辐式网络。纯轴辐式网络中要求非枢纽节点只与枢纽节点连接，且非枢纽节点间不允许直接连接。然而在实际应用中，不是每个OD对（起讫点）都必须经过枢纽中心进行中转运输，这样会产生绕道运输，成本与时间都会大幅增加，OD对间采取直达运输即可满足。由此，在混合轴辐式网络中放宽了对非枢纽节点间的约束，允许节点的连接不受限制，非枢纽节点既可以与枢纽节点连接，也可以进行非枢纽节点间的相互连通。

（二）模型假设

本文做出以下基本假设：不考虑由商品车的车型尺寸不一所引起的单位载运工具的装载数量不同，均以标准小汽车尺寸来计算；同一起讫点间的商品车不能分开运输；运输网络中一个城市节点处最多只能建立一个枢纽；无时间约束且不考虑整车提前到达或延误到达产生仓储成本或延误成本；默认该第三方整车物流企业临近主机厂的VDC为一个枢纽节点，且不考虑商品车在主机厂与整车分拨中心之间短驳运输产生的运输成本；RDC具有相同的容量限制。

（三）参数设置

基于混合轴辐式理论的整车物流多式联运网络优化模型中具体参数的定义如下：N—城市节点数；P—RDC枢纽节点个数；S—运输方式集合（S=1代表公路运输，S=2代表铁路运输，S=3代表水路运输）；Wij—表示从节点i到节点j的货物流量；Lsij—表示从节点i到节点j间采用运输方式s的实际运输距离；Csij—表示从节点i到节点j采用运输方式s的单位运输成本；Fk—表示枢纽节点k建设并投入运营的固定成本；Gk—表示在枢纽节点k选择改变运输方式的中转成本；α—表示规模经济效应的折扣系数，采用固定值；Uk—表示枢纽k的年最大储存能力。

轴辐式多式联运枢纽网络优化中的决策变量如下：

（四）模型构建

以网络运输总成本最小为目标函数，构建基于混合轴辐式理论的整车物流多式联运网络优化模型，模型表述如下：

上述模型中，公式（1）为以成本最优的目标函数，考虑了网络中基于起讫点间直接运输模式下和基于枢纽节点联合运输模式下的运输成本，枢纽节点的运营成本及枢纽节点处的中转运输成本四个部分。公式（2）表示起讫点间运输模式的选择，要么选择起讫点间的直接运输模式，否则选择基于枢纽接驳的联合运输模式。公式（3）表示运输网络中需要设置的枢纽节点个数。公式（4）和公式（5）表示基于枢纽接驳的联合运输模式下，限定节点i、j分别指派给枢纽节点k、m。公式（6）和公式（7）表示枢纽间节点k的容量限制。公式（8）表示网络节点和运输方式的取值范围约束。公式（9）表示成本折扣系数的取值范围约束。公式（10）表示决策变量的取值范围约束。

整车物流多式联运网络优化模型求解禁忌算法设计

禁忌搜索算法（Tabu Search，简称TS）最早是由Glover在1986年提出，TS算法的本质是对局部领域搜索算法的一种扩展，是运用邻域移动进行搜索的全局逐步寻优算法。迄今为止，TS在组合优化、神经网络、机器学习等领域广泛应用，与此同时，禁忌算法在求解轴辐式网络模型求解问题上也有很多应用案例，例如赵晏林（2013）、Ishfaq R等（2010）学者在轴辐式枢纽节点的设计中成功应用了TS算法并获得了良好的求解结果。

本文选择禁忌算法求解混合轴辐式整车多式联运网络优化模型，运用C#编程求解得到最优方案。

（一）算法关键要素设计

禁忌算法的基本要素包括初始解与编码、邻域结构、禁忌对象、禁忌长度、适配函数、特赦规则、终止规则等。

编码与初始解。目前对实际问题的编码主要形式有二进制编码、十进制编码、实数编码和自然数编码等多种编码方式。考虑求解结果的直观性，本文选择自然数编码，对各个城市利用自然数进行标号。与此同时，初始解随机产生。

邻域结构。定义邻域结构由单点替换而产生。让P为初始的选址点集合，N-P为未选点集合，则让P与N-P交换一个点所能产生的所有T*的集合，即为邻域，单点替换产生的邻域有P（N-P）个解集。

禁忌对象。由于禁忌算法是按照邻域移动搜索最优解，而邻域结构由单点替换而产生，因此禁忌是对换出节点作为对象进行禁忌。

禁忌长度。设定禁忌长度为之间的一个随机整数。

适配函数。实际问题的求解目标是物流网络总成本最低，因此把目标函数作为适配函数。

特赦规则。当出现迄今为止最好的解时特赦相应的禁忌点。

终止准则。以最佳适配值连续M代保持不变时，终止算法。

（二）算法流程设计

Step 1：初始化参数。对N个城市进行自然数编码，并对枢纽节点集合T的长度进行初始化，即P个枢纽，以及初始当前迭代步数与禁忌状态，令迭代次数t=0，tabu_status（i）=0。

Step 2：随机产生初始解，根据适配函数求得初始解的网络总物流成本CT，令当前最优解T=Tbest，最优解的网络总物流成本CTbest=CT。

Step 3：通过换出集合T的枢纽节点构造邻域N（T），并计算它的P（N-P）个解集所对应的总成本CT（i），i=1，2，…，P（N-P）。

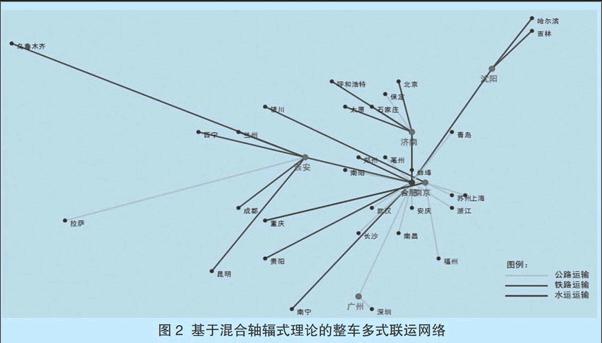
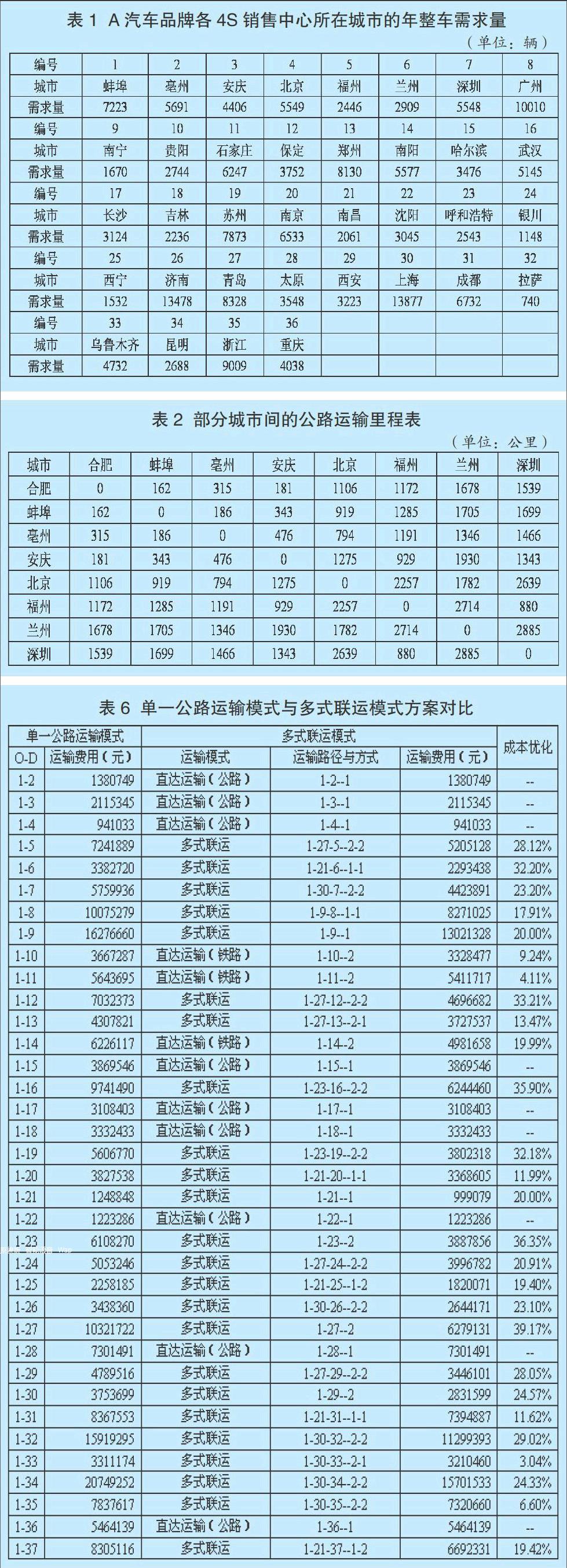
Step 4：检查邻域中最小的目标函数值CT（k）。如果tabu_status（k）=0或者CT（k）

Step 5：令t=t+1，如果CT（K）

Step 6：如果CTbest连续100代保持不变时，终止算法；否则，更新禁忌状态，即对所有tabu_status（i）>0的点，令tabu_status（i）= tabu_status（i）-1，返回Step 3。

仿真与分析

（一）数据准备

A汽车品牌拥有一个整车生产基地分布在合肥，该品牌商品车销售面向全国，其4S销售中心遍布于36个城市，各4S销售中心年整车需求量如表1所示。受制于篇幅长度，只显示部分城市间的公路和铁路运输里程如表2所示，各城市间的铁路和水路实际运输距离可通过《中国公路铁路水路图集》获得。公路、铁路和水路运输方式下，单商品车的运输费不同，其具体费率如表3所示。在枢纽处各运输方式可发生转换，会产生相应的换装成本，其单位换装成本如表4所示。其它数据如表5所示。

（二）仿真结果

运行Visual Studio导入基础数据，通过C#编程可得模型求解结果，最终模型求解结果如表6所示，由图2可知广州、南京、沈阳、济南和西安被选为枢纽。

优化后的整车物流网络具有以下四大特点：

一是相对于“点对点”直通式物流网络，基于混合轴辐式理论的整车物流多式联运网络的总运输费用明显要低，成本减少43951110元，约为原物流网络总成本的80%，如图3所示。

二是基于混合轴辐式理论的整车物流多式联运网络在降低成本的同时，可提供多样的运输组织方案，提高铁路和水路运输的比例，弱化其对公路运输的依赖，使其物流网络的运输结构得到优化。在优化后的物流网络中，整车运输形式仍以公路运输为主，但占比下降为53.51%，铁路运输为辅的趋势明显增强，发运规模将达到45%左右，由于在国内适合水路运输的航道较少且港口等基础设施不完善，水路运输比例不足3%，有待提升，如图4所示。

三是在优化后的物流网络中，原有OD对间的部分运输线路得到了优化。主要分为三种情况：第一种情形，原有直接采用公路运输的OD对，优化后选择了更为经济的铁路运输形式组织商品车发运，如表6中的1-10；第二种情形，原有直达的OD对优化后与同方向的其它需求点选择经过枢纽节点组织“干线运输+支线分拨”的运输方案，充分发挥干线运输的规模优势，提高运载工具利用率与发运频次，降低物流成本，如表6中的1-13；第三种情形，保证原有OD对间公路运输方式不变，选择经过枢纽节点享受规模效应带来的经济折扣，降低总成本。这种情形可以理解为，在干线上所聚集的大量货源便于第三方整车物流企业组织货源，可提高运载工具的满载率与发运频率，更有效地利用运载工具，减少空驶产生的额外运输成本。

四是布局RDC可有效缓解目前以合肥为始发点的库存压力，如图5所示，而且将RDC的布局更靠近消费市场，加快市场响应速度，缩短车辆交付周期，提高物流服务满意度。

结论

本文立足于第三方整车物流企业单一公路运输模式下高成本低效能的现实情况，以及克服新标准与法规对商品车公路运输方式带来的影响，借鉴广泛应用于航空运输业的轴辐式理论，为第三方整车物流企业构建基于混合轴辐式理论的整车物流多式联运网络优化模型，并运用启发式算法进行求解。从分析结果可知，优化后的整车多式联运网络运营成本明显下降，运载工具的利用率将会提高，便于组织商品车运输，与此同时，铁路运输发运规模明显上升，整车发运结构得到优化。此外，优化后的整车物流网络可帮助第三方整车物流企业转型升级，利于其围绕VDC与RDC整合物流资源，并提供多种整车运输解决方案，形成企业核心竞争力。

参考文献：

1.Roberto Baldacci.Recent exactalgorithms for solving the vehicle routing problem under capacity and time window constraints[J].European Journal of OperafionM Research，2011（6）

2.Lee C GIMarina A.Epelman，Chelsea C，et a1.A shortest path approach to the multiple-vehicle muting problem with split pick-ups[J].Transportation Research，Part B，2006（40）

3.侯玉梅，贾震环，田歆等.带软时间窗整车物流配送路径优化研究[J].系统工程学报，2015，30（2）

4.王书勤，黄茜.一种基于CVRP的改进蚁群算法[J].甘肃科技，2011，27（3）

5.钱丹，刘建胜，袁彬等.多车型联运整车物流配送优化模型及算法研究[J].制造业自动化，2015，37（6）

6.陈建岭，王栋.汽车整车物流区域配送中心综合选址方法研究[J].山东交通学院学报，2015，23（1）

7.赵欣.供应链环境下的整车物流资源整合研究[J].物流技术，2014，33（12）

8.陈蔚.铁路运输在商品车整车物流中的发展分析[J].铁道运输与经济，2011，33（7）

9.Okelly M E.A quadratic integer program for the location of interacting hub facilities[J].European Journal of Operational Research，1987，32（3）

10.郭莹莹.航空货运市场轴辐式网络构建博弈分析[J].武汉科技大学学报（社会科学版），2012，14（4）

11.谢婷，周骞，史鸽飞.基于时间可靠性分析的农产品轴辐式物流网络节点选址[J].长沙理工大学学报（自然科学版），2015，12（2）

12.李莉，丁以中.轴辐式快递网络的枢纽选址和分配优化[J].上海海事大学学报，2012，33（2）

13.李惠珠，宋海清，孟多.轴辐式零担运输网络中集送货线路规划研究[J].华南师范大学学报（自然科学版），2012，44（2）

14.赵晏林.基于混合轴辐式理论的港口物流多式联运网络优化[D].浙江工业大学，2013

15.Ishfaq R.Hub network design models for intermodal logistics[D].The University of Alabama TUSCALOOSA，2010