一道圆锥曲线教材例题的探究与引申
2017-01-10林泰凤范学基
林泰凤 范学基
(1.福州民族中学,福建福州350600;2.罗源第一中学,福建福州350600)
一道圆锥曲线教材例题的探究与引申
林泰凤1 范学基2
(1.福州民族中学,福建福州350600;2.罗源第一中学,福建福州350600)
高中数学教材中选用的例题大都值得在解题教学中进行探究与引申。笔者在实际教学中,引导学生对人教社普通高中课程标准实验教科书《数学·选修2—1(A版)》第41页例3进行探究与引申,让学生在触类旁通的过程中认识到许多知识间的联系,大大提高了学生的学习兴趣,培养了学生在探究中发现并提出数学问题的能力。
发散思维;探究学习
高中数学复习课中,大部分教师的处理策略是通过组织学生回忆构建章节知识体系,用例习题进行考点题型以及方法的讲练,以达到记忆理解知识和掌握技能方法的应试要求,在这个过程,虽然有不少教师对例题进行精选并相应变式,但多以覆盖考点题型为主,对例题的背景探究和引申拓展较少。本文尝试从一道课本例题的复习出发对学生进行引导反思逐步深化有关知识的认识理解,借以抛砖引玉。
在一节圆锥曲线复习课中,笔者选用了人教社2007年2月第2版普通高中课程标准实验教科书《数学·选修2—1(A版)》中第41页例3:如图1,设点A,B的坐标分别为(-5,0),(5,0)。直线AM,BM相交于点M,且它们的斜率之积是,求点M的轨迹方程。
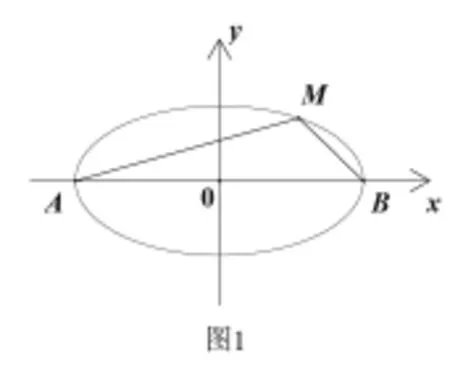
进一步引导学生思考,若把结论1中长轴两端点换成短轴两端点,结论还成立吗?换成一般的过椭圆中心的弦的两端点呢?答案是肯定的,让学生尝试证明,参考如下:
设M(x0,y0)是椭圆=1(a>b>0)上任意一点,AB是椭圆的任意一条过原点的弦,设
因此有如下推广结论:
特别地,若把圆看成椭圆中长轴长与短轴长相等的特殊情形,可得该斜率之积为定值。
圆锥曲线具有概念的统一性,那么椭圆的情形是否可以类比到双曲线?类似可证得如下结论:
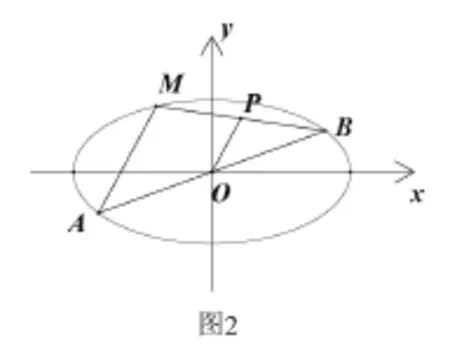
在得到上述结论后,再引导学生进行如下联想:上述结论2、3的讨论中若设点M是椭圆(或双曲线)上任意一点,AB(A,B,M三点不共线)是过椭圆(或双曲线)中心O的任意一条弦,取弦BM的中点P,如图2所示,则OP为△ABM的中位线,故OP∥AM,所以kOP=kAM,则由结论2、3,有kOP·kBM=kAM·kBM=-或)。因而,由上述讨论有如下推论:
结论2、3概括起来看就是由过定点(即中心)得对应连线的斜率的乘积为定值,再引导学生考虑并探究其逆命题是否成立,也就是若椭圆(或双曲线)上一点与动弦的两端点的连线的斜率之积为定值,能否得到该弦恒过定点?事实上,我们可得如下结论:
【结论4】(1)M(x0,y0)是椭圆=1(a>b>0)上一定点,A,B是椭圆上异于点M的两动点,若kAM·kBM=m(m为常数,m≠),则直线AB必过定点
(2)M(x0,y0)是双曲线=1(a>0,b>0)上一定点,A,B是双曲线上异于点M的两动点,若kAM·kBM=m(m为常数,m≠),则直线AB必过定点
以下证明(1):
设a(x1,y1),B(x2,y2),则现进行坐标平移,把点M(x0,y0)移到新坐标系的原点O′,即令,则在新坐标系XO′Y中,有原椭圆方程可化为,即,又∵点,故原椭圆方程可化为b2X2_2b2x0X+a2Y2+2a2y0Y=0。①设直线AB的方程为Y=kX+n,由已知点A,B异于点M,得n≠0。将直线AB的方程与方程①联立,整理得(b2+a2k2)X2+a(b2x0+a2kn+a2ky0)X+a2n2+2a2y0n=0。
由韦达定理得,X1+X2=,则,所以直线AB的方程为,故在新坐标系XO′Y中,直线AB过定点,所以在原坐标系中,直线AB过定点(,即点。证毕。
特别地,当m=-时,则直线AB过原点O;当m=-1,且点M为椭圆的左顶点时,则直线AB过定点
由此可以轻松解决以下例题:
例1.已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1。
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l;y=kx+m与椭圆C相交于A,B(A,B不是左右顶点),且AB为直径的圆过椭圆C的左顶点,求证:直线l过定点,并求出该定点的坐标。
证明如下:
设A(x1,y1),B(x2,y2),则tanα=kMA=,进行坐标变换,令X=x+a,Y=y,则 tanα=
由题知直线AB不垂直于x轴(否则α+β=π),设直线Ab的方程为Y=kX+n……②
若再把椭圆的情形类比到双曲线,类似可证得如下结论:
结论5、6可以归结为圆锥曲线上一动弦两端到同形状顶点(椭圆的左顶点,双曲线的右顶点和抛物线的顶点)的倾斜角的和为定值,则该弦所在直线过定点,其他非顶点的定点的情形又怎么样?还有,反之一定成立吗?另外可以发现结论5中α+β=情形的定点也就是结论4中k·k=m=1的定点AMBM的特殊情形,而α+β=θ(0<θ<π,θ≠)情形下的定点(此时为结论4中当m=-1,且点M为椭圆的左顶点时的情形)为极点的极线上,双曲线中也是如此情况,这里更深层次的联系是什么,为什么这样,还有待进一步探究,限于篇幅在此不再展开。
[1]沈文选,张垚,冷岗松.奥林匹克数学中的几何问题[M].长沙:湖南师范大学出版社,2009.
[2]余明芳,王钦敏.例谈高中数学探究性课题的选择与教学设计[J].数学通报,2015(11).
[3]章建跃.数学·选修2—1(A版)[M].北京:人民教育出版社,2007.
(责任编辑:王钦敏)
