一道有关反比例函数题的多样解法

向晓琳● 胡泽明●

湖北省秭归县归州镇初级中学(443601)



一道有关反比例函数题的多样解法

向晓琳● 胡泽明●

湖北省秭归县归州镇初级中学(443601)

一、真题回放

如图1，点A(m，m+1)，点B(m+3，m-1)都在反比例函数y=k/x(x>0)的图象上.(1)求m，k的值；(2)如图2，过点B作BC⊥x轴于C，在A与B之间，是否存在一点P，使得△POC和△OAB的面积相等？若存在，请写出直线OP的解析式；否则说明理由；(3)如图3，过点A作AM⊥y轴于M，过点B作BN⊥x轴于N，连接MN，MN与AB的位置关系如何？

二、解法呈现

(1)∵点A(m，m+1)，点B(m+3，m-1)都在反比例函数y=k/x(x>0)的图象上，

∴m(m+1)=(m+3)(m-1)，解得m=3，∴k=12.

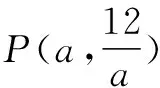
(3)法一 ：比较k值法

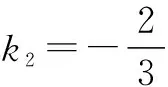
∴k1=k2,∴MN∥AB.

法二：利用平行线的判定来做

过A作AR垂直于x轴，过B作BR平行于x轴，AR与BR交于R，延长AB交x轴于Q.如图3-1所示,

▶

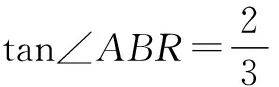
法三：利用平行四边形的性质来做

过A作AG⊥MN于G,过B作BP⊥MN于P，连接OA,OB,AN,BM.如图3-2所示,

易证S△AMO=S△AMN,S△BNO=S△BNM,S△AMO=S△BNO，∴S△AMN=S△BNM.

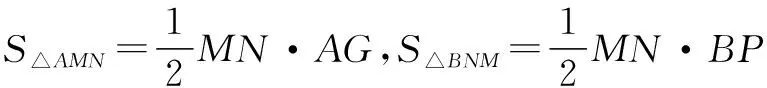
∵AG⊥MN，BP⊥MN，∴AG∥BP. ∴四边形AGPB是平行四边形,∴MN∥AB.

三、问题升华

图3中的点A，点B如果是两动点，MN和AB仍然平行，解法同(3).

总之，任何数学题无论是解法单一，还是解法多样，只要用心思考，融会贯通，都会柳暗花明，迎刃而解的.

G632

B

1008-0333(2016)35-0005-02