浅谈解题后的反思

四川省资阳市雁江区第二中学 张绪忠

浅谈解题后的反思

四川省资阳市雁江区第二中学 张绪忠

我们在学习数学知识过程中，都要做一定的练习和习题，对一些具有代表性的题型在解后还应进行反思，通过不断解题后反思，既能对已学知识进行巩固，又能进一步对所学知识进行升华，以扩大学习成果。那么解题后应反思些什么呢？同学们可从以下几个方面来进行反思。

一、思联系

解题后反思解题中所联系到的基础知识，使之起到复习巩固的作用，又能发掘新旧知识的联系。

例1 如图（1）所示，AD为△ABC的高，AE是△ABC的外接圆直径，求证：AB·AC=AE·AD。

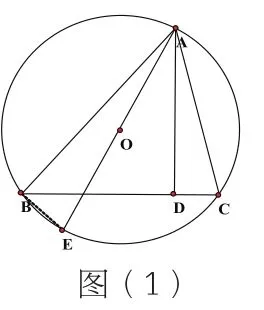
证明：连接BE。

证题完后，再反思一下，发现运用了直径所对圆周角为90°、相似三角形的判定和性质等知识，从而达到运用新知识、巩固旧知识的目的，使新旧知识交替螺旋上升。

二、思多解

有许多几何题一题多解，因而解完一道题后，应进一步反思是否还有别的解法，从中找出最优的解法，打破思维定式，培养发散思维能力。

如例1，除以上证明外，还可以连接EC，如图（2），证明△ABD∽△AEC，可得

三、思规律

解题后，反思解题方法有无一般规律，能否从个体中提炼出共性，有利于强化知识的运用，提高数学学习的效率。

如例1证明中，主要有两个规律：一是要证明等积式通常化为比例式来分析；二是有关圆中的直径问题，通常需要添加辅助线构成直径上的圆周角，只要有这两个方面的题目，都可按这个规律去分析。

四、思变化

解题后，反思适当改变原题的条件与结论或图形的运动变化，使一题多变，拓宽思路，培养创新思维能力。

例2 已知等腰三角形的周长为16，其中一边是6，求另两条边长。此题可进行一题多变。

变式一：已知等腰三角形一腰长为6，周长为16，求底边长。

变式二：已知等腰三角形一边长为4，另一边长为6，求周长。

变式三：已知等腰三角形一边长为3，另一边长为6，求周长。

变式四：已知等腰三角形的腰长为a，求底边x的取值范围。

变式五：已知等腰三角形的腰长为x，底边长为y，周长是16，写出y与x的函数关系式。

五、思同类

解题后，反思与该题同类的习题，通过类比，达到掌握解决这一类题的目的，使数学的类比思想扎根于解题之中，又能从题海中解脱出来。

规律与方法：几个非负数的和为0，则每个非负数都为0。利用这个规律与方法可以解以下的题组：

六、思失误

解题后，要反思解答题目中的关键字词、有无隐含条件，总结应该注意的问题，减少失误。

例4 已知方程2x²+mx-2m+1=0的两个实数根的平方和是，求m的值。

解：设方程2x²+mx-2m+1=0的两根为x1、x2，

因此，平时就应养成解题后反思的良好习惯，并不断总结经验教训，努力提高自己数学解题的技能技巧，加强发散思维和创新思维的训练，促进知识与能力的不断提升，养成良好的学习习惯，提高数学学习的效率。