基于灰色关联分析法及GSA-LSSVM的汽轮机排汽焓预测模型
2017-01-10王惠杰范志愿许小刚李鑫鑫
王惠杰,范志愿,许小刚,李鑫鑫
(华北电力大学能源动力与机械工程学院,河北省保定市 071003)
基于灰色关联分析法及GSA-LSSVM的汽轮机排汽焓预测模型
王惠杰,范志愿,许小刚,李鑫鑫
(华北电力大学能源动力与机械工程学院,河北省保定市 071003)
排汽焓是汽轮发电机组热经济性诊断必不可少的一个参数。通过汽轮机功率方程与灰色关联分析(grey correlation analysis,GCA)理论确定了模型的输入变量,利用万有引力搜索算法(gravitational search algorithm,GSA)优化了最小二乘支持向量机(least squares support vector machine,LSSVM)的惩罚因子μ以及核径向范围σ2个参数。通过比较分析,选用RBF_kernel为LSSVM的核函数。以GCA-GSA-LSSVM为基础,建立了预测汽轮机排汽焓的数学模型,并将其与BP神经网络、RBF神经网络进行对比,同时分析了该数学模型的鲁棒性。结果表明基于GCA-GSA-LSSVM的汽轮机排汽焓预测模型具有精度高、泛化能力强、鲁棒性强等优点,该方法为精确预测机组节能潜力提供了一种有力的工具。
最小二乘支持向量机(LSSVM);万有引力搜索算法(GSA);灰色关联分析法(GCA);汽轮机排汽焓
0 引 言
在深度节能的背景下,正确的热经济指标才能精准地预测机组的节能潜力。机组的各个热经济指标都与汽轮机的排汽焓有密切的关系。由于汽轮机的排汽为湿蒸汽,并且无法直接测量蒸汽的湿度。所以,汽轮机排汽焓无法由现场测点数据直接得到。因此,准确地预测汽轮机排汽焓是当前亟待解决的一个实际工程问题。
关于汽轮机排汽焓的计算问题,国内外学者从不同的角度进行了研究。从热力学角度出发,提出了能量平衡法、等焓节流法、冷凝法等计算方法[1-6]。能量平衡法根据机组的实发功率、蒸汽流量、各段抽汽焓值计算汽轮机的排汽焓。使用能量平衡法计算汽轮机排汽焓时,蒸汽流量不容易被确定。根据节流原理,使湿蒸汽经过节流后变为等焓值的过热蒸汽。利用过热蒸汽的温度、压力可得到蒸汽对应的焓。此方法通常需要将节流后的压力控制在很低的范围内,在工程中不易实现。用冷却水将湿蒸汽冷却为饱和水,通过热平衡方程可以计算出相应的焓值,但是,该方法的实现过程较为复杂。利用离心力将湿蒸汽中的液滴分离出去,计算出蒸汽的湿度,进而得出湿蒸汽的焓值。若湿蒸汽中的液滴太小,很难保证将其全部分离出去,计算结果的准确性也得不到保证。根据入射光在不同的介质中产生不同散射特性的原理,可以通过入射光的散射特性辨识出蒸汽的湿度,进而得到湿蒸汽的焓值。但是,光学仪器的应用范围有限,且设备昂贵。随着人工智能算法的不断发展,神经网络算法被大量地应用于汽轮机排汽焓预测研究中[7-9]。训练样本空间越大,神经网络算法的预测结果越精确。工程中的训练样本空间有限,所以该算法在实际应用中受到了一定的限制。与神经网络算法相似,支持向量机能够逼近任意非线性函数,训练输入与输出变量之间的黑箱模型[10-13]。最小二乘支持向量机(least squares support vector machine,LSSVM)是一种改进的支持向量机,降低了算法的复杂度[14-17],被广泛地应用于各种工程中。
为了避免累积误差,模型的输入变量必须能够由现场测点准确地获得。本文通过功率方程与灰色关联分析法(grey correlation analysis,GCA)确定模型的输入参数。利用万有引力搜索算法(gravitational search algorithm,GSA)优化最小二乘支持向量机的惩罚因子μ以及核径向范围σ2个参数。通过比较分析,选用RBF_kernel为LSSVM的核函数。以GCA-GSA-LSSVM为基础,建立预测汽轮机排汽焓的数学模型,并将其与BP神经网络、RBF神经网络进行对比,同时分析该数学模型的鲁棒性。
1 灰色关联分析法
在灰色关联分析法中,样本的决策属性被称为母序列,条件属性被称为子序列。在样本空间中,一段时间内的母序列与子序列都呈现出不同的曲线。灰色关联分析法通过判断各个子序列曲线与母序列曲线之间的形状,得出它们之间的关联度。子序列曲线与母序列曲线越相似,其关联度越高;反之,则关联度越低。灰色关联分析法的步骤如下详述。
步骤(1)在样本空间中确定子序列与母序列,样本空间的表示方法如式(1)所示。
(1)
式中:Y为母序列;X为子序列;xl(k)为第l个子序列的第k个元素;y(k)为母序列的第k个元素;L为序列长度。
步骤(2)为了避免量纲对关联性分析结果的影响,必须对各个序列进行无量纲化。本文采用式(2)进行无量纲化。
(2)
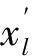
步骤3:计算子序列与母序列各个对应元素的相似因子Slk,以及样本空间中子序列与母序列的最大相似因子Smax与最小相似因子Smin,如式(3)所示。
(3)
步骤4:计算子序列与母序列各个元素之间的关联系数ξlk,如式(4)所示。
(4)
式中:ρ为系统分辨率,一般取0.5。
步骤5:计算各个子序列与母序列的关联度cl,如式(5)所示。
(5)
2 最小二乘支持向量机
LSSVM是支持向量机(support vector machine,SVM)的一种改进算法,其继承了SVM能够逼近任意非线性函数、鲁棒性强等优点[11]。LSSVM还具有计算简单、运算速度快、能够避免维数灾难等优点。因此,LSSVM具有广泛的工程应用前景。
由式(1)可知,在k时刻下的样本可以描述为 {x1(k),x2(k),…,xl(k),y(k)},其中x(k)为模型输入参数,y为输出参数。在实际工程中,样本经常为线性不可分类型。LSSVM通过非线性映射函数φ(x)将样本映射到高维空间中[12],使其线性可分。LSSVM的回归模型可以表示为式(6)所示的形式,即
y(k)=wTφ[x(k)]+b
(6)
式中:w为将x(k)映射到高维空间中的权重函数向量;b为系数。
LSSVM根据结构风险最小化理论将上述回归模型转化为式(7)所示的优化问题[13]。
(7)
式中:μ为惩罚因子;δ(k)为回归模型的误差。
由式(7)可见,上述问题为有约束的优化问题。LSSVM通过拉格朗日法将其转化为无约束条件的优化问题。并且,将原问题映射到其对偶空间,如式(8)所示:
(8)
式中λ(k)为拉格朗日乘子。
由式(8)以及Karush-Kuhn-Tucker条件可得到式(9):
(9)
将式(9)中的w、δ(k)消去,可得到式(10)所示的线性方程组:
(10)
式中:H为L阶单位矩阵;K为L阶矩阵。
式(10)中的K[x(i),x(j)]为核函数,LSSVM可以选用3种核函数,分别为LIN_kernel、RBF_kernel和POLY_kernel。
求解式(10)可得到拉格朗日乘子λ和系数b以及LSSVM的回归模型,如式(11)所示:

(11)
3 万有引力搜索算法
GSA是由克尔曼沙希德·巴霍纳尔大学Esmat Rashedi教授提出的[18]。GSA是模仿宇宙中各个质点间存在万有引力的一种全局优化算法。空间中的每一个质点都代表一个可行解。质点的质量越大,表明该质点越接近最优解。空间中的各个质点通过引力交换信息,逐步实现向最优解靠拢。GSA的寻优原理如下详述。
假设在搜索空间中有Z个质点,每个质点都是n维向量。t时刻第i个质点Xi(t)的表示方法如式(12)所示:
(12)
GSA利用适应度fi(t)比较质点的优劣。若优化问题求最小值,全局最优适应度b(t)和最差适应度w(t)的定义如式(13)所示,若优化问题求最大值,b(t)和w(t)的定义如式(14)所示:
(13)
(14)
质点的惯性质量Mi(t)由式(15)确定:
(15)
t时刻的引力常量G(t)与初始引力值G0、衰减因子α有关,如式(16)所示:
(16)
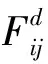
(17)
式中:Rij(t)为2个质点之间欧几里得距离的平方;ε为无穷小量。

(18)
式中:rand为[0,1]的随机数。
(19)
GSA的寻优过程如图1所示。
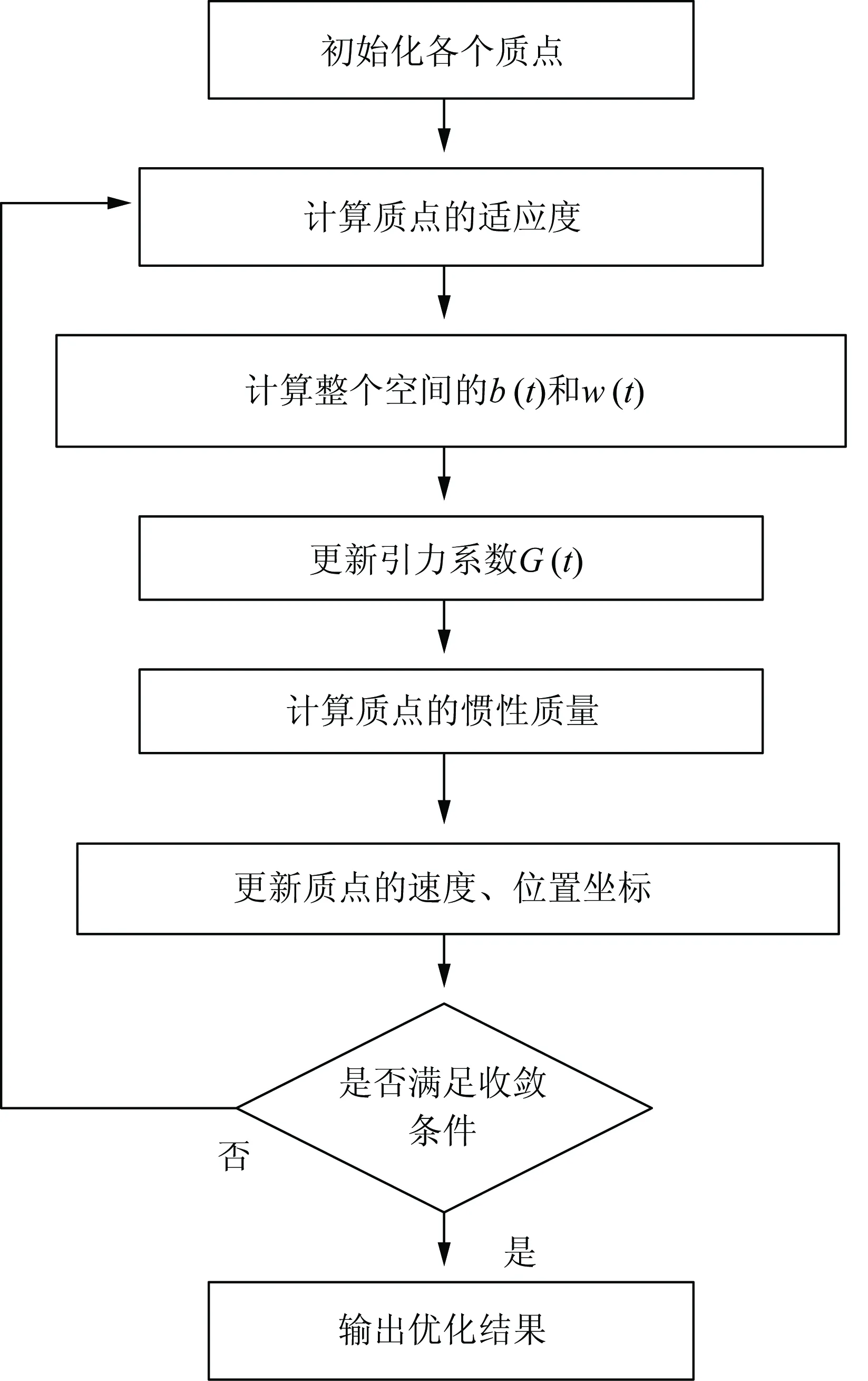
图1 GSA的寻优流程图
4 数学模型
4.1 输入与输出参数确定
本文主要研究排汽焓的预测,所以排汽焓为模型的输出参数。汽轮机功率方程如式(20)所示:
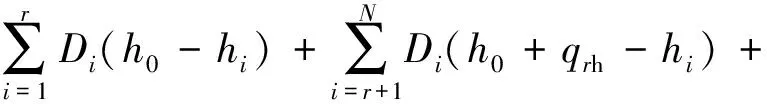
(20)
式中:W为汽轮机功率, kW;r为再热之前的抽汽级数;Di为第i级的抽汽流量,kg·s-1;h0为主蒸汽焓,kJ·kg-1;hi为第i级的抽汽焓,kJ·kg-1;N为总共的抽汽级数;qrh为再热蒸汽的焓增,kJ·kg-1;Dc为汽轮机的排汽流量,kg·s-1;hc为汽轮机排汽焓,kJ·kg-1。
由式(20)可见,汽轮机排汽焓可以表示为式(21)所示的形式:
hc=f(W,Di,Dc,h0,hi,qrh)
(21)
为了避免计算过程中的累积误差,模型输入参数采用现场有测点、能够被准确测量的变量。由文献[19]可知,汽轮机的汽水分布状态由机组的拓扑结构、各级加热器抽汽焓、给水出口焓、疏水焓、给水流量决定。机组运行过程中,其拓扑结构不发生变化。过热抽汽焓由压力、温度tm决定。湿蒸汽抽汽焓由抽汽压力、湿度决定。由于湿度并不能直接测量,所以在输入参数中只考虑湿蒸汽压力。加热器给水出口焓由给水的压力、出口温度twi决定。低加的给水压力用凝结水泵出口压力pwc表示,高加的给水压力用给水泵出口压力pgs表示。在不考虑抽汽压损的情况下,疏水焓由相应的抽汽压力pi和疏水出口温度todi决定。由于流量不易被准确测量,所以在本研究中,各种流量都不被考虑。主蒸汽焓由主蒸汽压力p0、温度t0决定。再热蒸汽焓增由再热器的入口焓与出口焓决定。再热器入口焓一般与某一级抽汽焓相等。再热器出口焓由再热器出口压力prh和温度trh决定。
综上所述,影响排汽焓的因素如式(22)所示:
(22)
式中:twc为凝结水泵出口温度,℃;g为过热区的抽汽级数。
本文以国产320 MW机组2016年1月的2 000条经过预处理的实际运行数据为建模样本。其中,前1 500条为训练模型样本,后500条为验证样本。以汽轮机排汽焓为母序列,式(22)所述的变量为子序列,由灰色关联分析法判定各个变量与汽轮机排汽焓的关联度,计算结果如表1所示。
由表1可见,相比于抽汽压力与排汽焓的关联度,抽汽温度与排汽焓的关联度更大。各级加热器出口水温比疏水出口温度与排汽焓的关联度大。
由统计学相关理论可知,关联度大于0.9表明变量之间呈现强烈的相关性。因此,将关联度大于0.9的16个变量作为模型的输入参数。
4.2 核函数选取
核函数对LSSVM的回归精度、泛化能力都有很大的影响。3种核函数都有各自的优越性,并且在不同的工程问题中都有应用。由上述分析可知,汽轮机排汽焓与t0、trh等16个变量有关。所以,不能简单地由理论分析确定出哪种核函数最适合于汽轮机排汽焓预测模型。本文在LSSVM平台上建立预测汽轮机排汽焓的数学模型。在其它参数都取系统默认值的情况下,比较由3种核函数建立汽轮机排汽焓预测模型在训练过程中的相对误差以及标准差,如表2所示。
表1 各变量与排汽焓的关联度
Table 1 Correlation degree of each variable and exhaust enthalpy
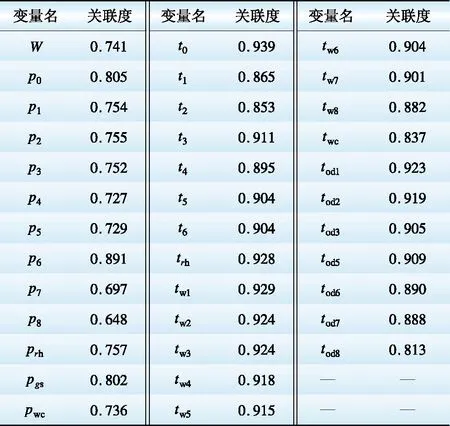
表2 不同核函数模型的相对误差以及标准差
Table 2 Relative error and standard deviation of models with different kernel function

由表2可见,RBF_kernel核函数建立的数学模型的相对误差以及标准差都小于POLY_kernel和LIN_kernel核函数建立的模型的相对误差以及标准差。因此,本研究采用RBF_kernel核函数。
4.3 μ和σ优化
在LSSVM的RBF_kernel核函数中,μ和σ是2个最重要的参数。惩罚因子μ是衡量算法复杂度与模型精度的指标。μ越大,模型精度越高,算法的复杂度越大;μ越小,模型精度越低,算法的复杂度越小。因此,必须寻求一个能使算法复杂度与模型精度平衡的μ。σ表示RBF_kernel核函数的径向范围。
采用表3中的6个函数测试GSA的性能,测试函数参考文献[18]。其中:f1和f2为单峰高维函数;f3和f4为多峰高维函数;f5和f6为多峰低维函数。
表3 GSA性能测试函数
Table 3 Test functions of GSA performance

在函数f4中,函数u的定义如式(23)所示:
(23)
在测试过程中,采用文献[18]的相关数据设置算法的各个参数。在函数f1、f2、f3、f4中,自变量维数n取为30。GSA的参数设置如下:空间中的质点数为50;最大迭代次数为1 000;引力常量初始值G0为100;衰减因子α为20。
各个测试函数的真实最小值fR以及GSA搜索得到的最小值fG如表4所示。
表4 GSA性能测试结果
Table 4 Test results of GSA performance
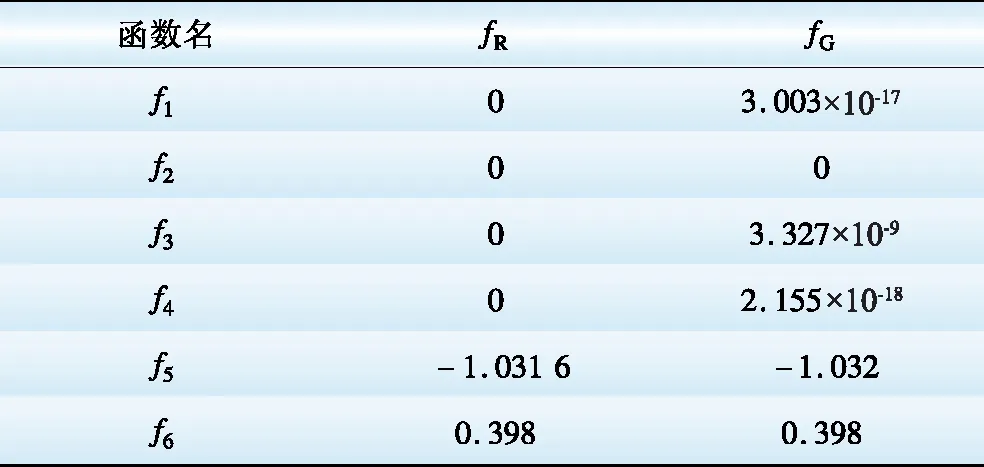
由表4可见,函数f2、f6的fG与fR一致,函数f1、f3、f4、f5的fG与fR非常接近。因此,GSA完全能够满足工程计算的精度要求。
利用GSA优化μ和σ。μ的取值范围为[0.1,100 00],σ的取值范围为[0.01,100][20]。质点的适应度取为模型训练过程中相对误差均值的绝对值。μ、σ优化前后,训练模型过程的相对误差Δhc如图2所示。

图2 模型相对误差对比图
由图2可见,μ和σ优化前,Δhc分布在 [-0.268,0.310];μ和σ优化后,Δhc分布在 [-0.115,0.134]。因此,μ和σ的优化是有效的。惩罚因子μ优化后为8 311.1,核径向范围σ优化后为2.345。
5 实例应用
5.1 排汽焓预测
由上述分析可知,本文选取RBF_kernel为核函数,μ取为8 311.1,σ取为2.345。利用国产320 MW机组的2 000条经过数据预处理的实际运行数据建立模型。用前1 500条数据训练模型,后500条数据验证模型的精度。
为了客观地描述变量与排汽焓之间的关系,建模之前由式(24)对各个变量归一化。
(24)
式中:x′为变量归一化后的值;x为变量原始值;xmin为样本中该变量的最小值;xmax为样本中该变量的最大值。
由式(25)对数学模型的预测值反归一化。
x=xmin+x′(xmax-xmin)
(25)
排汽焓的预测相对误差Δhct如图3所示。
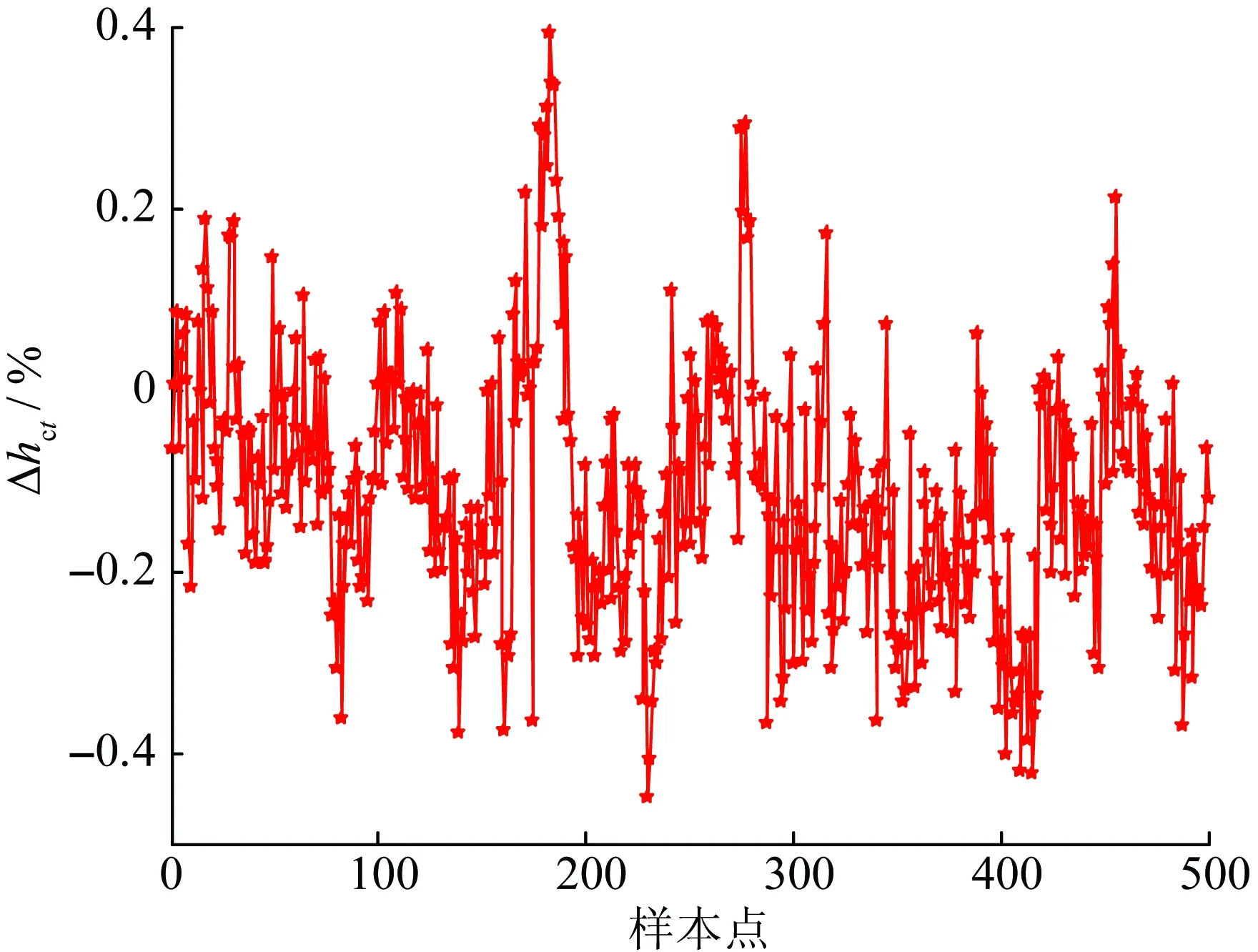
图3 预测排汽焓的相对误差
由图3可见,排汽焓的预测相对误差绝大部分在0.4%以内,能够满足工程计算的精度要求。
5.2 模型比较
LSSVM能够逼近任意非线性函数,建立输入变量与输出变量的黑箱模型,在工程中得到了广泛的应用。BP神经网络和RBF神经网络与LSSVM的功能类似。本文比较了GCA-GSA-LSSVM和BP神经网络、RBF神经网络在预测排汽焓方面的应用情况。在不同训练样本数情况下,3种模型的训练相对误差Δhc和预测相对误差Δhct如表5所示。
表5 3种模型的Δhc和Δhct
Table 5 Δhcand Δhctof three models

由表5可见,RBF模型的Δhc远远小于GCA-GSA-LSSVM和BP模型的Δhc。BP模型Δhc的平均值为0.076,GCA-GSA-LSSVM模型Δhc的平均值为0.035。RBF模型的Δhct远远大于GCA-GSA-LSSVM和BP模型的Δhct。BP模型Δhct的平均值为0.224,GCA-GSA-LSSVM模型Δhct的平均值为0.134。因此,RBF模型的泛化能力最差,不易用于预测汽轮机排汽焓。BP模型和GCA-GSA-LSSVM模型的泛化能力较强。但是,GCA-GSA-LSSVM模型的训练相对误差和预测相对误差均小于BP模型的训练相对误差和预测相对误差。所以,GCA-GSA-LSSVM模型与BP和RBF神经网络模型相比,具有更高的预测精度以及更强的泛化能力。
5.3 鲁棒性分析
在实际工程中,测点不可避免地会受到外界的各种干扰。模型除了应该具有较高的精度外,还必须具有一定的抵御外界干扰的能力,即模型的鲁棒性。由表1可知,主蒸汽温度t0、1号加热器出口水温tw1、再热蒸汽温度trh、2号加热器出口水温tw2是与汽轮机排汽焓关联度最大的4个变量。对4个变量分别施加5%的随机噪声后,模型的预测相对误差Δhct如图4所示。
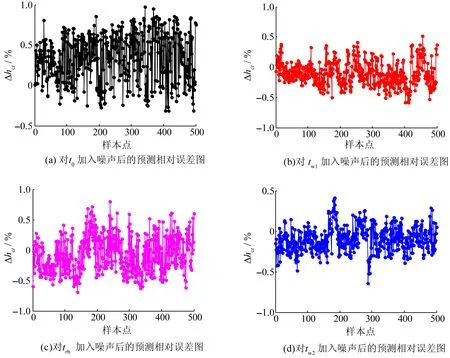
图4 加噪声后的模型预测相对误差
由图4可见,对t0、tw1、trh、tw2加入5%的随机噪声后,模型的预测相对误差仍能够保持在1%以内。由此可见,基于GCA-GSA-LSSVM的汽轮机排汽焓预测模型具有较强的鲁棒性。
6 结 论
(1)通过功率方程与灰色关联分析法确定了与排汽焓关联度在90%以上的16个变量。在建模过程中,比较了各种核函数建立的模型的相对误差以及标准差,选取RBF_kernel为LSSVM的核函数。通过万有引力搜索算法对惩罚因子μ及核径向范围σ进行了优化。
(2)利用建立好的GCA-GSA-LSSVM模型预测汽轮机的排汽焓,绝大部分误差在0.4%以内。比较了GCA-GSA-LSSVM模型、BP和RBF神经网络模型在排汽焓预测方面的应用情况。结果表明,GCA-GSA-LSSVM模型具有更高的预测精度和更强的泛化能力。对t0、tw1、trh、tw2加入5%的随机噪声后,模型的预测相对误差仍能够保持在1%以内,表明基于GCA-GSA-LSSVM的汽轮机排汽焓预测模型具有较强的鲁棒性。
[1]张乐乐, 张燕平, 黄树红, 等. 汽轮机湿蒸汽区蒸汽焓值的计算模型研究[J]. 动力工程学报, 2013, 33(4): 272-277, 302. ZHANG Lele, ZHANG Yanping, HUANG Shuhong, et al. Steam enthalpy calculation model for wet steam region of steam turbines[J]. Journal of Chinese Society of Power Engineering, 2013, 33(4): 272-277, 302.
[2]杨涛, 胥建群, 张赟, 等. 电站汽轮机低压缸排汽焓近似计算模型研究[J]. 热力透平, 2013, 42(1): 30-34. YANG Tao, XU Jianqun, ZHANG Yun, et al. Research on approximate calculation model of LP steam turbine exhaust enthalpy in power plant [J].Thermal Turbine, 2013, 42(1): 30-34.
[3]李勇, 李仁杰, 曹丽华, 等. 凝汽式汽轮机低压缸相对内效率在线监测方法[J]. 化工机械, 2014, 41(3): 316-322. LI Yong, LI Renjie, CAO Lihua, et al. On-line monitoring method for internal efficiency ratio of low-pressure cylinder in condensing steam turbine[J].Chemical Engineering & Machinery, 2014, 41(3): 316-322.
[4]闫顺林, 徐鸿, 李永华, 等. 汽轮机排汽焓动态在线计算模型的研究[J]. 动力工程, 2008, 28(2): 181-184, 199. YAN Shunlin, XU Hong, LI Yonghua, et al. Research on online dynamic model for calculating exhaust enthalpy of steam turbine[J]. Journal of Power Engineering, 2008, 28(2): 181-184, 199.
[5]韩中合, 杨昆, 田松峰, 等. 在线确定凝汽式汽轮机排汽焓的热力学方法[J]. 动力工程, 2004, 24(3): 356-359, 374. HAN Zhonghe, YANG Kun, TIAN Songfeng. A thermodynamics method of online calculation steam turbine exhaust enthalpy[J]. Power Engineering, 2004, 24(3): 356-359, 374.
[6]徐曙. 用Baumman公式估算汽轮机排汽压力对机组经济性的影响[J]. 汽轮机技术, 2016, 58(1): 72-74, 32. XU Shu. Estimate exhaust pressure of steam turbine on the economic impact with Baumman formula[J].Turbine Technology, 2016, 58(1): 72-74, 32.
[7]宫唤春. 基于双隐层径向基过程神经网络的汽轮机排汽焓在线预测[J]. 热力发电, 2014, 43(7): 32-35. GONG Huanchun. Double hidden layer RBF process neural network based online prediction of steam turbine exhaust enthalpy[J]. Thermal Power Generation, 2014, 43(7): 32-35.
[8]吴俊杰, 侯宏娟, 杨勇平. 神经网络算法在汽轮机排汽焓估算中的应用[J]. 热力发电, 2014, 43(8): 125-130. WU Junjie, HOU Hongjuan, YANG Yongping. Application of neural network algorithm in steam turbine’s exhaust enthalpy estimation[J].Thermal Power Generation, 2014, 43(8): 125-130.
[9]王建国, 赵帅, 王广雨. 提高汽轮机排汽焓在线预测精度的GA-Elman神经网络算法[J]. 热力发电, 2014, 43(10): 90-94. WANG Jianguo, ZHAO Shuai, WANG Guangyu. A GA-Elman neural network algorithm which can improve online prediction accuracy of exhaust enthalpy for steam turbines[J]. Thermal Power Generation, 2014, 43(10): 90-94.
[10]蔡杰进, 马晓茜. 支持向量机在电站汽轮机排汽焓在线预测中的应用[J]. 电力系统自动化, 2006, 30(18): 77-82. CAI Jiejin, MA Xiaoqian. Online forecasting of steam turbine exhaust enthalpy based on support vector machine method[J]. Automation of Electric Power Systems, 2006, 30(18): 77-82.
[11]王绵斌, 李欢欢, 谭忠富,等. 基于支持向量机方法的输电工程造价指标评估体系[J]. 电力建设, 2014, 35(3):102-106. WANG Mianbin, LI Huanhuan, TAN Zhongfu, et al. Index evaluation system of power transmission project cost based on support vector machine method[J]. Electric Power Construction,2014, 35(3):102-106.
[12]李红玲, 文习山, 舒乃秋. 最小二乘支持向量机在绝缘子污秽放电声发射监测中的应用[J]. 电力建设, 2009, 30(6):25-28. LI Hongling, WEN Xishan, SHU Naiqiu.Application of least squares support vector machine in acoustic emission monitor of polluted insulator discharge [J]. Electric Power Construction, 2009, 30(6):25-28.
[13]韩中合, 焦宏超, 朱霄珣,等. 基于EEMD排列组合熵的SVM转子振动故障诊断研究[J]. 电力建设, 2016, 37(1):92-96. HAN Zhonghe, JIAO Hongchao, ZHU Xiaoxun, et al. SVM rotor vibration fault diagnosis based on EEMD permutation entropy [J]. Electric Power Construction,2016, 37(1):92-96.
[14]田中大, 高宪文, 石彤. 用于混沌时间序列预测的组合核函数最小二乘支持向量机[J]. 物理学报, 2014, 63(16):66-76. TIAN Zhongda, GAO Xianwen, SHI Tong. Combination kernel function least squares support vector machine for chaotic time series prediction[J].Acta Physica Sinica, 2014, 63(16):66-76.
[15]顾燕萍, 赵文杰, 吴占松. 最小二乘支持向量机鲁棒回归算法研究[J]. 清华大学学报(自然科学版), 2015, 55(4):396-402. GU Yanping, ZHAO Wenjie, WU Zhansong. Investigation of robust least squares-support vector machines[J].Journal of Tsinghua University (Science and Technology), 2015, 55(4):396-402.
[16]孟银凤, 梁吉业. 基于最小二乘支持向量机的函数型数据回归分析[J]. 模式识别与人工智能, 2014, 27(12):1124-1130. MENG Yinfeng, LIANG Jiye. Regression analysis for functional data based on least squares support vector machine[J]. Pattern Recognition and Artificial Intelligence, 2014, 27(12):1124-1130.
[17]潘宇雄, 任章, 李清东. 动态贝叶斯最小二乘支持向量机[J]. 控制与决策, 2014, 29(12): 2297-2300. PAN Yuxiong, REN Zhang, LI Qingdong. Dynamic Bayesian least squares support vector machine[J]. Control and Decision,2014, 29(12): 2297-2300.
[18]RASHEDI E, NEZAMABADI-POUR H, SARYAZDI S. GSA: a gravitational search algorithm [J]. Information Sciences, 2009, 179(13): 2232-2248.
[19]张春发, 张素香,崔映红,等. 现行电力系统热经济性状态方程[J]. 工程热物理学报, 2001, 22(6): 665-667. ZHANG Chunfa, ZHANG Suxiang, CUI Yinghong, et al. Thermo-economy state equation of modern power system[J]. Journal of Engineering Thermophysics, 2001, 22(6): 665-667.
[20]刘超, 牛培峰, 游霞. 反向建模方法在汽轮机热耗率建模中的应用[J]. 动力工程学报, 2014, 34(11): 867-872, 902. LIU Chao, NIU Peifeng, YOU Xia. Application of reversed modeling method in prediction of steam turbine heat rate[J].Journal of Chinese Society of Power Engineering, 2014, 34(11): 867-872, 902.
(编辑 景贺峰)
Prediction Model of Steam Turbine Exhaust Enthalpy Based on Grey Correlation Analysis Method and GSA-LSSVM
WANG Huijie,FAN Zhiyuan,XU Xiaogang,LI Xinxin
(School of Energy, Power and Mechanical Engineering, North China Electric Power University,Baoding 071003, Hebei Province, China)
The steam exhaust enthalpy is an essential parameter for the thermal economic diagnosis of steam turbine generator group. We determine the input variables of the model by steam turbine power equation and grey correlation analysis (GCA) method, and optimize the punishment factorμand nuclear radial rangeσof least square support vector machine (LSSVM) by gravitation search algorithm (GSA). The RBF_kernel is selected as the kernel function of LSSVM through the comparative analysis. Based on the GCA-GSA-LSSVM, this paper establishes the mathematical model to predict the exhaust enthalpy of steam turbine, compares it with the BP neural network and RBF neural network, and analyzes its robustness. The results show that the prediction model of steam turbine exhaust enthalpy based on GCA-GSA-LSSVM has the advantages of high precision, strong generalization ability and strong robustness. This method provides a powerful tool for accurately predicting the energy saving potential of the unit.
least square support vector machine (LSSVM); gravitation search algorithm(GSA); grey correlation analysis method(GCA); steam turbine exhaust enthalpyl
中央高校基本科研业务费专项资金资助项目(12NQ40);北京市自然科学基金项目(3132028)
TM 621
A
1000-7229(2016)11-0115-08
10.3969/j.issn.1000-7229.2016.11.017
2016-07-27
王惠杰(1972),男,博士,副教授,主要从事能源利用与节能技术、热力发电厂系统、设备和运行节能在线监测及指导系统的研究与开发工作;
范志愿(1990),男,硕士研究生,本文通信作者,主要从事电厂节能、机组优化运行以及数据挖掘的研究工作;
李鑫鑫(1992),女,硕士研究生,主要从事数据挖掘工作;
许小刚(1979),男,博士,高级工程师,主要从事电厂数据挖掘、机组优化运行、信号处理及故障诊断的研究与开发工作。
Project supported by Fundamental Research Funds for the Central Universities (12NQ40);Beijing Natural Science Foundation (3132028)
